中考复习第一轮—圆专题教案 15页

专题——圆 ‎——中考复习第一轮 中考考试说明：略 核心考点解读 核心考点：圆周角 知识难度：★★☆☆☆‎ 考察频率：★★★★★‎ 主要题型：选择题、填空题、解答题 内容：‎ 圆周角定律：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。相等的圆周角所对的弧也相等；‎ 推论：半圆（或直径）所对的圆周角是直角，90度的圆周角所对的弦是直径。‎ 核心考点：垂径定理 知识难度：★★☆☆☆‎ 考察频率：★★★☆☆‎ 主要题型：选择题、填空题、解答题、证明题 内容：‎ 垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。‎ 推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。‎ 推论2：弦的垂直平分线经过圆心，并且平分弦所对的两条弧。‎ 推论3：平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。‎ 核心母题 知识链接：圆周角定理 思路方法：运用圆周角定理将所求角转化为已知角和能直接由已知角求出的角。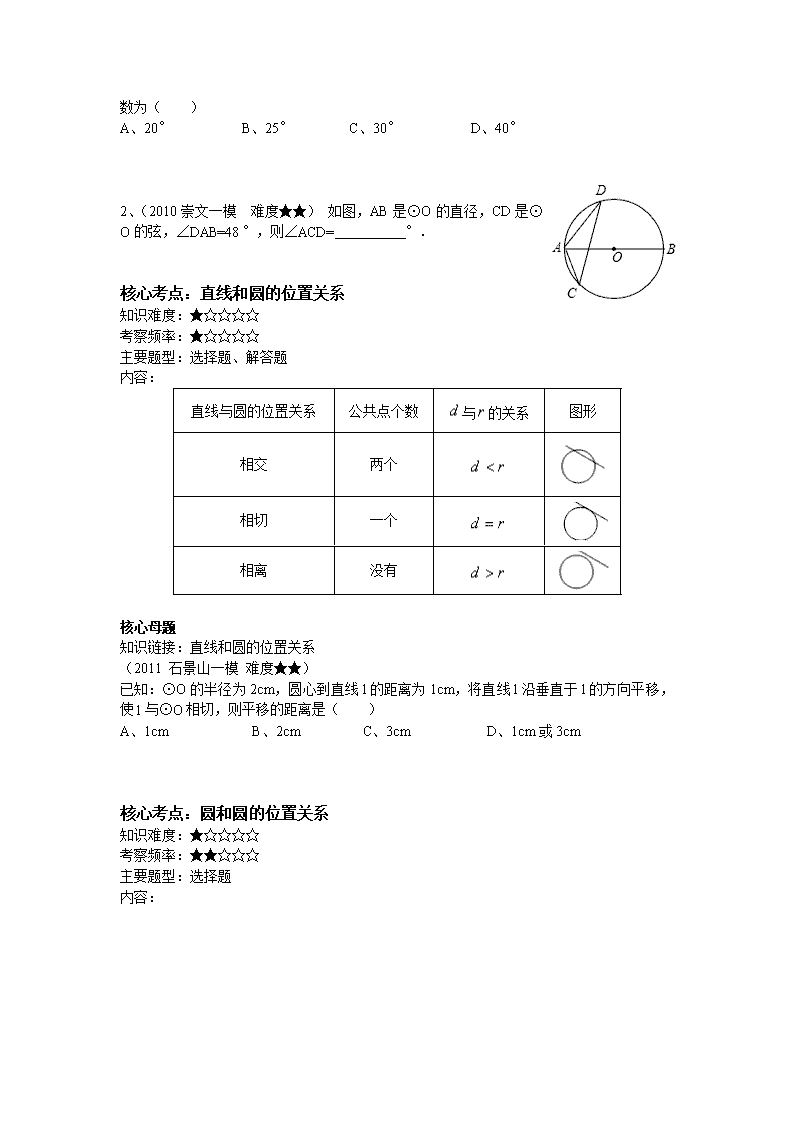‎ ‎1.（2010 朝阳一模 难度★） 如图，AB为⊙O的直径，CD为弦，AB⊥CD，如果∠BOC=70°，那么∠A的度数为（　B　）‎ A、70° B、30° C、35° D、20°‎ ‎2、（2011 丰台二模 难度★★）如图，BD是⊙O的直径，‎ ‎∠CBD=30°，则∠A的度数为（　C　）‎ A、30° B、45° C、60° D、75°‎ 巩固练习：‎ ‎1、（2010年石景山一模 难度★★）已知：如图，AB切⊙O于点B，OA与⊙O交于点C，点P在⊙O上，若∠BAC=40°，则∠‎ BPC的度数为（　　）‎ A、20° B、25° C、30° D、40°‎ ‎2、（2010崇文一模 难度★★） 如图，AB是⊙O的直径，CD是⊙O的弦，∠DAB=48°，则∠ACD= °．‎ 核心考点：直线和圆的位置关系 知识难度：★☆☆☆☆‎ 考察频率：★☆☆☆☆‎ 主要题型：选择题、解答题 内容：‎ 直线与圆的位置关系 公共点个数 与的关系 图形 相交 两个 相切 一个 相离 没有 核心母题 知识链接：直线和圆的位置关系 ‎（2011 石景山一模 难度★★）‎ 已知：⊙O的半径为‎2cm，圆心到直线l的距离为‎1cm，将直线l沿垂直于l的方向平移，使l与⊙O相切，则平移的距离是（　　）‎ A、‎1cm B、‎2cm C、‎3cm D、‎1cm或‎3cm 核心考点：圆和圆的位置关系 知识难度：★☆☆☆☆‎ 考察频率：★★☆☆☆‎ 主要题型：选择题 内容：‎ 核心母题 知识链接：圆和圆的位置关系 ‎1、（2008北京中考 难度★）若两圆的半径分别是‎1cm和‎5cm，圆心距为‎6厘米，则这两圆的位置关系是（ ）‎ A.内切 B.相交 C.外切 D.外离 ‎ ‎2、（2009东城一模 难度★★）‎ 如图，点O在⊙A外，点P在线段OA上运动．以OP为半径的⊙O与⊙A的位置关系不可能是下列中的（　　）‎ A、外离 B、相交 C、外切 D、内含 巩固练习：‎ ‎（20011西城二模 难度★）‎ 两圆的半径分别为‎3cm和‎5cm，若圆心距为‎2cm，则这两圆的位置关系是（ ）‎ A.内含 B.相交 C.外切 D.内切 核心考点：弧长、扇形面积、圆锥的侧面积 知识难度：★☆☆☆☆‎ 考察频率：★☆☆☆☆‎ 主要题型：选择题 内容：‎ 弧长：的圆心角所对的弧长为 扇形面积：圆心角为的扇形面积 圆锥的侧面积：（l为母线长，r是底面圆半径）‎ 核心母题 ‎ 知识链接：圆锥的侧面积公式 ‎（2011 东城一模 难度★★）‎ 已知圆锥的母线长为4，底面半径为2，则圆锥的侧面积等于（ ）‎ A.11 B‎.10‎ C.9 D.8‎ 巩固练习：‎ ‎（2009朝阳一模 难度★★）‎ 如图，圆锥的高AO为12，母线AB长为13，则该圆锥的侧面积等于（ ）‎ A、36π B、27π C、65π D、9π 核心考点：圆的切线 知识难度：★★☆☆☆‎ 考察频率：★★★★★‎ 主要题型：解答题 内容：‎ 切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。‎ 切线的性质定理：圆的切线垂直于过切点的半径。‎ 切线长定理：从圆外一点可以引两条圆的切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。‎ 核心母题1：‎ 知识链接：平行线；圆切线的判定定理；解直角三角形 常见错误：不会通过平行来说明待证切线和半径之间的垂直关系；不会进行角的等量代换；不会解直角三角形。‎ ‎（2010海淀一模 难度★★★）‎ 已知：如图，⊙O为△ABC的外接圆，BC为⊙O的直径，作射线BF，使得BA平分∠CBF，过点A作AD⊥BF于点D．‎ ‎（1）求证：DA为⊙O的切线；‎ ‎（2）若BD=1，tan∠BAD=，求⊙O的半径．‎ 巩固练习：‎ ‎（2009年 密云一模 难度★★★）‎ 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．‎ ‎（1）求证：AE是⊙O的切线；‎ ‎（2）若∠DBC=30°，DE=‎1cm，求BD的长．‎ 核心母题2：‎ 知识链接：圆切线的判定定理；解直角三角形；垂径定理。‎ 常见错误：不会进行角的等量代换以至于无法说明待证切线和半径直径的垂直关系；不会解直角三角形。‎ ‎（2010崇文一模 难度★★★）‎ 如图，AB是半圆O的直径，过点O作弦AD的垂线交半圆O于点E，交AC于点C，使∠BED=∠C．‎ ‎（1）判断直线AC与圆O的位置关系，并证明你的结论；‎ ‎（2）若AC=8，cos∠BED=，求AD的长．‎ 巩固练习：‎ ‎（2010 宣武一模 难度★★★）‎ 已知：如图，⊙O是△ABC的外接圆，AB为⊙O直径，且PA⊥AB于点A，PO⊥AC于点M ‎（1）求证：PC是⊙O的切线；‎ ‎（2）当OM=，cosB=时，求PC的长．‎ 核心母题3：‎ 知识链接：平行线；圆切线的判定定理；锐角三角函数；相似三角形。‎ 常见错误：不会通过平行来说明待证切线和半径之间的垂直关系；不会运用三角形相似和方程思想求解三角形中的线段。‎ 已知：如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．‎ ‎（1）求证：AC与⊙O相切；‎ ‎（2）当BD=2，sinC=时，求⊙O的半径．‎ 巩固练习：‎ ‎（2009年 北京中考 难度★★★）‎ 已知：如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．‎ ‎（1）求证：AE与⊙O相切；‎ ‎（2）当BC=4，cosC= 时，求⊙O的半径．‎ 核心母题4：‎ 知识链接：平行线；圆切线的判定定理； 三角形相似。‎ 思路方法：运用三角形相似（一般为两直角三角形的相似）列出含有待求线段的比例式求解。‎ 常见错误：不会通过平行来说明待证切线和半径之间的垂直关系；不会运用三角形相似和求解三角形中的线段。‎ ‎（2011 海淀二模 难度★★★）‎ 已知AB是⊙O的直径，C是⊙O上一点（不与A、B重合），过点C作⊙O的切线CD，过A作CD的垂线，垂足是M点．‎ ‎（1）如图1，若CD∥AB，求证：AM是⊙O的切线．‎ ‎（2）如图2，若AB=6，AM=4，求AC的长．‎ 巩固练习：‎ ‎（2010 石景山一模 难度★★★）‎ 已知：如图，AB为⊙O的直径，弦AC∥OD，BD切⊙O于B，连接CD．‎ ‎（1）判断CD是否为⊙O的切线，若是请证明；若不是请说明理由；‎ ‎（2）若AC=2，OD=6，求⊙O的半径．‎ 综合练习：‎ ‎1、（2011 北京中考 难度★★★）‎ 如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=∠CAB．‎ ‎（1）求证：直线BF是⊙O的切线；‎ ‎（2）若AB=5，sin∠CBF= ，求BC和BF的长．‎ ‎2、（2010 北京中考 难度★★★）‎ 已知：如图，在△ABC中，D是AB边上一点，圆O过D、B、C三点，∠DOC=2∠ACD=90°．‎ ‎（1）求证：直线AC是圆O的切线；‎ ‎（2）如果∠ACB=75°，圆O的半径为2，求BD的长．‎ ‎3、（2008 北京中考 难度★★★）‎ 已知：如图，在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC，AB分别交于点D，E，且∠CBD=∠A．‎ ‎（1）判断直线BD与⊙O的位置关系，并证明你的结论；‎ ‎（2）若AD：AO=8：5，BC=2，求BD的长．‎ ‎4、（2011 海淀一模 难度★★★）‎ 如图，AB为⊙O的直径，AB=4，点C在⊙O上，CF⊥OC，且CF=BF．‎ ‎（1）证明BF是⊙O的切线；‎ ‎（2）设AC与BF的延长线交于点M，若MC=6，求∠MCF的大小．‎ ‎5、（2009 通州一模 难度★★★）‎ 如图，△ABE中，AB=AE，以AB为直径作⊙O交BE于C，过C作CD⊥AE于D，DC的延长线与AB的延长线交于点P．‎ ‎（1）求证：PD是⊙O的切线；‎ ‎（2）若AE=5，BE=6，求DC的长． ‎ ‎6、（2011 海淀一模 难度★★★）‎ 如图，AB为⊙O的直径，AB=4，点C在⊙O上，CF⊥OC，且CF=BF．‎ ‎（1）证明BF是⊙O的切线；‎ ‎（2）设AC与BF的延长线交于点M，若MC=6，求∠MCF的大小．‎ ‎7、（2010 昌平一模 难度★★★）‎ 已知：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且OA=AB=AD．‎ ‎（1）求证：BD是⊙O的切线；‎ ‎（2）若点E是劣弧BC上一点，AE与BC相交于点F，且BE=8，tan∠BFA= ，求⊙O的半径长．‎ ‎8、（2010 西城一模 难度★★★）‎ 如图，△ABC内接于⊙O，且AB=AC，点D在⊙O上，AD⊥AB于点A，AD与BC交于点E，F在DA的延长线上，且AF=AE．‎ ‎（1）试判断BF与⊙O的位置关系，并说明理由；‎ ‎（2）若AD=4， ，求BC的长。‎ ‎9、（2011 石景山一模 难度★★★）‎ 已知：如图，在矩形ABCD中，点O在对角线BD上，以OD的长为半径的⊙O与AD，BD分别交于点E、点F，且∠ABE=∠DBC．‎ ‎（1）判断直线BE与⊙O的位置关系，并证明你的结论；‎ ‎（2）若 ，CD=2，求⊙O的半径．‎ ‎10、（2011 东城一模 难度★★★）‎ 已知：AB是⊙O的弦，OD⊥AB于M交⊙O于点D，CB⊥AB交AD的延长线于C．‎ ‎（1）求证：AD=DC；‎ ‎（2）过D作⊙O的切线交BC于E，若DE=2，CE=1，求⊙O的半径．‎ ‎11、（2009 东城一模 难度★★★）‎ ‎10、已知：如图，在△ABC中，AB=AC，点D是边BC的中点．以BD为直径作圆O，交边AB于点P，连接PC，交AD于点E．‎ ‎（1）求证：AD是圆O的切线；‎ ‎（2）若PC是圆O的切线，BC=8，求DE的长．‎ ‎12、（2011 昌平一模 难度★★★）‎ 已知：如图，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，若∠AEC=∠ODB．‎ ‎（1）求证：BD是⊙O的切线；‎ ‎（2）当AB=10，BC=8时，求BD的长．‎ ‎13、（2010 朝阳一模 难度★★★）如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，DB=‎6‎cm．‎ ‎（1）求证：AC是⊙O的切线；‎ ‎（2）求⊙O的半径长；‎ ‎（3）求由弦CD、BD与弧BC所围成的阴影部分的面积（结果保留π）．‎ ‎14、（2011 丰台一模 难度★★★）在Rt△AFD中，∠F=90°，点B、C分别在AD、FD上，以AB为直径的半圆O过点C，连接AC，将△AFC沿AC翻折得△AEC，且点E恰好落在直径AB上．‎ ‎（1）判断：直线FC与半圆O的位置关系是 ；并证明你的结论．‎ ‎（2）若OB=BD=2，求CE的长．‎ ‎15、（2009 丰台一模 难度★★★））如图，点D是⊙O直径CA的延长线上一点，点B在⊙O上，且AB=AD=AO．‎ ‎（1）求证：BD是⊙O的切线；‎ ‎（2）若点E是劣弧BC上一点，弦AE与BC相交于点F，且CF=9，cos∠BFA=，求EF的长．‎