中考数学专题复习三角形与全等三角形学生版 9页

‎2013年中考数学专题复习第十七讲 三角形与全等三角形 ‎【基础知识回顾】‎ 三角形的概念：‎ ‎ 1、由 直线上的三条线段 组成的图形叫三角形 ‎ 2、三角形的基本元素：三角形有 条边 个顶点 个内角 二、三角形的分类：‎ ‎ 按边可分为 三角形和 三角形，按角可分为 三角形 三角形 三角形 ‎【名师提醒：等边三角形属于特殊的 三角形，锐角三角形和钝角三角形有事称为 三角形】‎ 三、三角形的性质：‎ ‎ 1、三角形的内角和是 三角形的任意一个外角 和它不相得两个内角的和三角形的一个外角 任意一个和它不相邻的内角 ‎ 2、三角形任意两边之和 第三边，任意两边之差 第三边 ‎ 3、三角形具有 性 ‎【名师提醒：1、三角形的外角是指三角形一边和另一边的 组成的角，三角形有 个外角，三角形的外角和事 ，是其中 各外角的和 ‎ ‎2、三角形三边关系定理是确定三条线段否构成三角形和判断限度间不等关系的主要依据】‎ 四、三角形中的主要线段：‎ ‎ 1、角平分线：三角形的三条角平分线都在三角形 部 且交于一点，这些是三角形的 心 它到 得距离相等 ‎ 2、中线：三角形的三条中线都在三角形 部，且交于一点 ‎ 3、高线：不同三角 形 的 三 条高线位置不同，锐角三角形三条高都连三角形 直角三角形有一条高线在 部，另两条河 重合，钝角三角形有一条高线在三角形 部，两条在三角形 部 ‎4、中位线：连接三角形任意两边 的线段叫做三角形的中位线。‎ ‎ 定理：三角形的中位线 第三边且等于第三边的 ‎ ‎【名师提醒：三角形的平分线、中线、高线、中位线都是 且都有 条】‎ 五、全等三角形的概念和性质：‎ ‎ 1、 的两个三角形叫做全等三角形 ‎ 2、性质：全等三角形的 、 分别相等，全等三角形的对应线段（角平分线、中线、高线）周长、面积分别对应 ‎ ‎【名师提醒：全等三角形的性质是证明线段、角等之间数量关系的最主要依据】‎ 一、 全等三角形的判定：‎ ‎1、一般三角形的全等判定方法：①边角边，简记为 ②角边角：简记为 ③角角边：简记为 ④边边边：简记为 ‎ ‎2、直角三角形的全等判定除可用一般三角形全等判定的所有方法以外，还可以用 来判定 ‎【名师提醒：1、判定全等三角形的条件中，必须至少有一组 对应相等，用SAS判定全等，切记角为两边的 ‎ ‎ 2、判定全等三角形的有关条件要特别注意对应两个字】‎ ‎【重点考点例析】‎ ‎ 考点一：三角形内角、外角的应用 例1 （2012•南通）如图，△ABC中，∠C=70°，若沿图中虚线截去∠C，则∠1+∠2=（　　）‎ A．360° B．250° C．180° D．140°‎ 对应训练 ‎1．（2012•泉州）如图，在△ABC中，∠A=60°，∠B=40°，点D、E分别在BC、AC的延长线上，则∠1= °．‎ ‎ 考点二：三角形三边关系 例2 （2012•泸州）已知三角形两边的长分别是3和6，第三边的长是方程x2-6x+8=0的根，则这个三角形的周长等于（　　）‎ A．13 B．‎11 ‎‎ C．11 或13 D．12或15‎ 对应训练 ‎1．（2012•义乌市）如果三角形的两边长分别为3和5，第三边长是偶数，则第三边长可以是（　　）‎ A．2 B．3 C．4 D．8‎ 考点三：三角形全等的判定 例3 （2012•乐山）如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，有下列结论：‎ ‎①△DFE是等腰直角三角形；‎ ‎②四边形CEDF不可能为正方形；‎ ‎③四边形CEDF的面积随点E位置的改变而发生变化；‎ ‎④点C到线段EF的最大距离为．‎ 其中正确结论的个数是（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎ 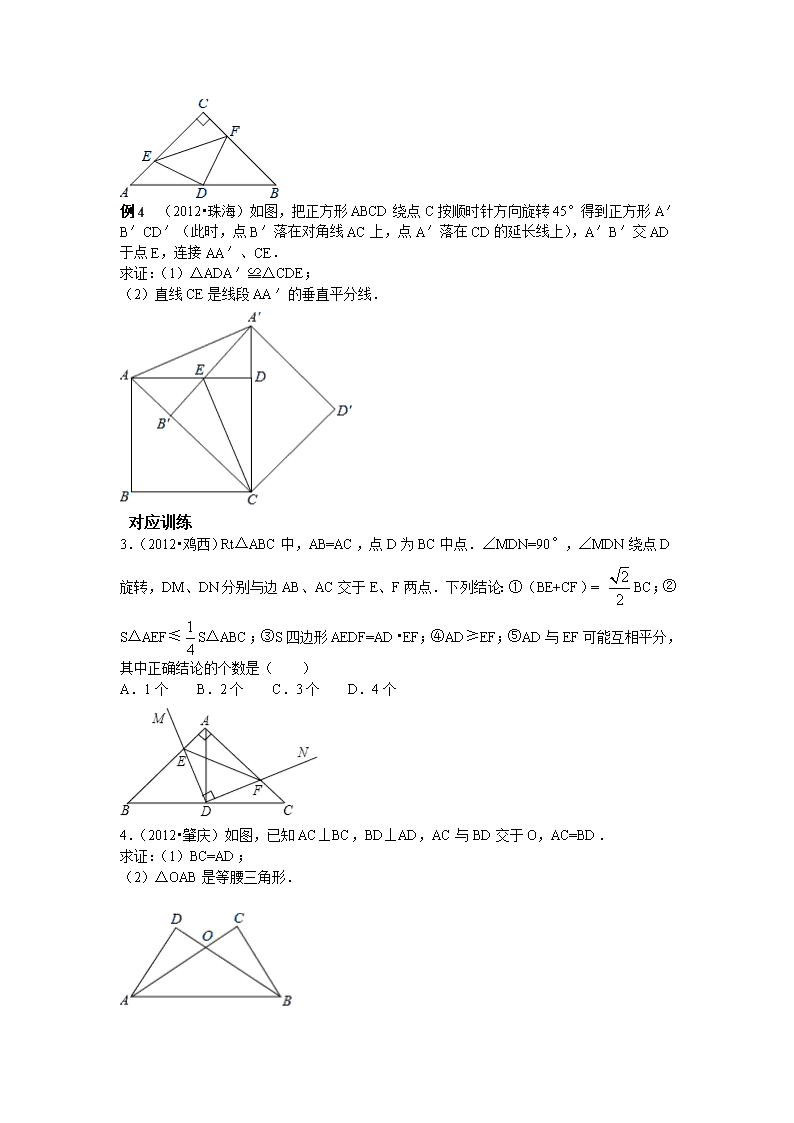例4 （2012•珠海）如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′（此时，点B′落在对角线AC上，点A′落在CD的延长线上），A′B′交AD于点E，连接AA′、CE．‎ 求证：（1）△ADA′≌△CDE；‎ ‎（2）直线CE是线段AA′的垂直平分线．‎ 对应训练 ‎3．（2012•鸡西）Rt△ABC中，AB=AC，点D为BC中点．∠MDN=90°，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下列结论：①（BE+CF）= BC；②S△AEF≤S△ABC；③S四边形AEDF=AD•EF；④AD≥EF；⑤AD与EF可能互相平分，其中正确结论的个数是（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎ ‎4．（2012•肇庆）如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．‎ 求证：（1）BC=AD；‎ ‎（2）△OAB是等腰三角形．‎ 考点四：全等三角形开放性问题 例5 （2012•义乌市）如图，在△ABC中，点D是BC的中点，作射线AD，在线段AD及其延长线上分别取点E、F，连接CE、BF．添加一个条件，使得△BDF≌△CDE，并加以证明．你添加的条件是 ．（不添加辅助线）．‎ 对应训练 ‎5．（2012•衡阳）如图，AF=DC，BC∥EF，请只补充一个条件，使得△ABC≌△DEF，并说明理由．‎ ‎【备考真题过关】‎ 一、选择题 ‎1．（2012•云南）如图，在△ABC中，∠B=67°，∠C=33°，AD是△ABC的角平分线，则∠CAD的度数为（　　）‎ A．40° B．45° C．50° D．55°‎ ‎2．（2012•梅州）如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC沿着DE折叠压平，A与A′重合，若∠A=75°，则∠1+∠2=（　　）‎ A．150° B．210° C．105° D．75°‎ ‎3．（2012•漳州）将一副直角三角板，按如图所示叠放在一起，则图中∠α的度数是（　　）‎ A．45° B．60° C．75° D．90°‎ ‎4．（2012•广东）已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（　　）‎ A．5 B．‎6 ‎‎ C．11 D．16‎ ‎5．（2012•郴州）以下列各组线段为边，能组成三角形的是（　　）‎ A．‎1cm，‎2cm，‎4cm B．‎4cm，‎6cm，‎8cm C．‎5cm，‎6cm，‎12cm D．‎2cm，‎3cm，‎5cm ‎ ‎6．（2012•玉林）如图，在菱形ABCD中，对角线AC，BD相交于点O，且AC≠BD，则图中全等三角形有（　　）‎ A．4对 B．6对 C．8对 D．10对 ‎7．（2012•贵阳）如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（　　）‎ A．∠BCA=∠F B．∠B=∠E C．BC∥EF D．∠A=∠EDF 三、填空题 ‎8．（2012•呼和浩特）如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC= ．‎ ‎9．（2012•娄底）如图，FE∥ON，OE平分∠MON，∠FEO=28°，则∠MFE= 度．‎ ‎10．（2012•白银）如图，在△ABC中，AC=BC，△ABC的外角∠ACE=100°，则∠A= 度．‎ ‎11．（2012•绥化）若等腰三角形两边长分别为3和5，则它的周长是 ．‎ ‎12．（2012•柳州）如图，在△ABC中，BD是∠ABC的角平分线，已知∠ABC=80°，则∠DBC= °．‎ ‎13．（2012•绵阳）如图，BC=EC，∠1=∠2，要使△ABC≌△DEC，则应添加的一个条件 为 ．（答案不唯一，只需填一个）．‎ 三、解答题 ‎14．（2012•铜仁地区）如图，E、F是四边形ABCD的对角线BD上的两点，AE∥CF，AE=CF，BE=DF．求证：△ADE≌△CBF．‎ ‎15．（2012•赤峰）如图所示，在△ABC中，∠ABC=∠ACB．‎ ‎（1）尺规作图：过顶点A作△ABC的角平分线AD；（不写作法，保留作图痕迹）‎ ‎（2）在AD上任取一点E，连接BE、CE．求证：△ABE≌△ACE．‎ ‎16．（2012•重庆）已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．‎ ‎1．（2012•扬州）如图，在四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD，垂足为E．求证：BE=DE．‎ ‎　‎ ‎2．（2012•镇江）如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF=∠ADF．‎ ‎（1）求证：△ADE≌△BFE；‎ ‎（2）连接EG，判断EG与DF的位置关系并说明理由．‎ ‎　‎ ‎3．（2012•佛山）如图，已知AB=DC，DB=AC ‎（1）求证：∠ABD=∠DCA．注：证明过程要求给出每一步结论成立的依据．‎ ‎（2）在（1）的证明过程中，需要作辅助线，它的意图是什么？‎ ‎4．（2012•滨州）如图1，l1，l2，l3，l4是一组平行线，相邻2条平行线间的距离都是1个单位长度，正方形ABCD的4个顶点A，B，C，D都在这些平行线上．过点A作AF⊥l3于点F，交l2于点H，过点C作CE⊥l2于点E，交l3于点G．‎ ‎（1）求证：△ADF≌△CBE；‎ ‎（2）求正方形ABCD的面积；‎ ‎（3）如图2，如果四条平行线不等距，相邻的两条平行线间的距离依次为h1，h2，h3，试用h1，h2，h3表示正方形ABCD的面积S．‎ ‎　‎ ‎5．（2012•长春）感知：如图①，点E在正方形ABCD的边BC上，BF⊥AE于点F，DG⊥AE于点G，可知△ADG≌△BAF．（不要求证明）‎ 拓展：如图②，点B、C分别在∠MAN的边AM、AN上，点E、F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC，求证：△ABE≌△CAF．‎ 应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为　6　．‎ ‎　‎ ‎6．（2012•阜新）（1）如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°．‎ ‎①当点D在AC上时，如图1，线段BD、CE有怎样的数量关系和位置关系？直接写出你猜想的结论；‎ ‎②将图1中的△ADE绕点A顺时针旋转α角（0°＜α＜90°），如图2，线段BD、CE有怎样的数量关系和位置关系？请说明理由．‎ ‎（2）当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时，使线段BD、CE在（1）中的位置关系仍然成立？不必说明理由．‎ 甲：AB：AC=AD：AE=1，∠BAC=∠DAE≠90°；‎ 乙：AB：AC=AD：AE≠1，∠BAC=∠DAE=90°；‎ 丙：AB：AC=AD：AE≠1，∠BAC=∠DAE≠90°．‎ ‎7．（2012•内江）已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作菱形ADEF（A、D、E、F按逆时针排列），使∠DAF=60°，连接CF．‎ ‎（1）如图1，当点D在边BC上时，求证：①BD=CF；②AC=CF+CD；‎ ‎（2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；‎ ‎（3）如图3，当点D在边BC的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD之间存在的数量关系．‎