- 12.62 MB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
(分类)滚动小专题(十一)与圆有关的计算与证明
类型 1 与圆的基本性质有关的计算与证明
(2018·安徽)20.如图,⊙O 为锐角△ABC 的外接圆,半径为 5.
(1)用尺规作图作出∠BAC 的平分线,并标出它与劣弧 BC 的交点 E(保留作图痕迹,不写作法);
(2)若(1)中的点 E 到弦 BC 的距离为 3,求弦 CE 的长.
解:(1)画图略
(2)∵AE 平分∠BAC
∴弧 BE=弧 EC,连接 OE
则 OE⊥BC 于点 F,EF=3
连接 OC、EC
在 Rt△OFC 中,由勾股定理可得 FC= 21
在 Rt△EFC 中,由勾股定理可得 CE= 30
(2018 湖州)
21.(8 分)(2018•湖州)如图,已知 AB 是⊙O 的直径,C,D 是⊙O 上的点,OC∥BD,交 AD 于点
E,连结 BC.
(1)求证:AE=ED;
(2)若 AB=10,∠CBD=36°,求 的长.
(2018 无锡)24、(本题满分 8 分)如图,四边形 ABCD 内接于圆心 O,AB=17,CD=10,∠A=90°,
cos B=
5
3 ,求 AD 的长。
【解答】
DA⊥AB
∠DAB=90°
在圆 O 中
∠DCB=90°
延长 AD、BC 交于点 E,易证∠B=∠EDC
5
3
ED
DC
3
50ED
5
3cos B
3
4tan B
在△EAB 中,EA=
3
68
3
417
DA=EA-ED=
3
50
3
68 =6
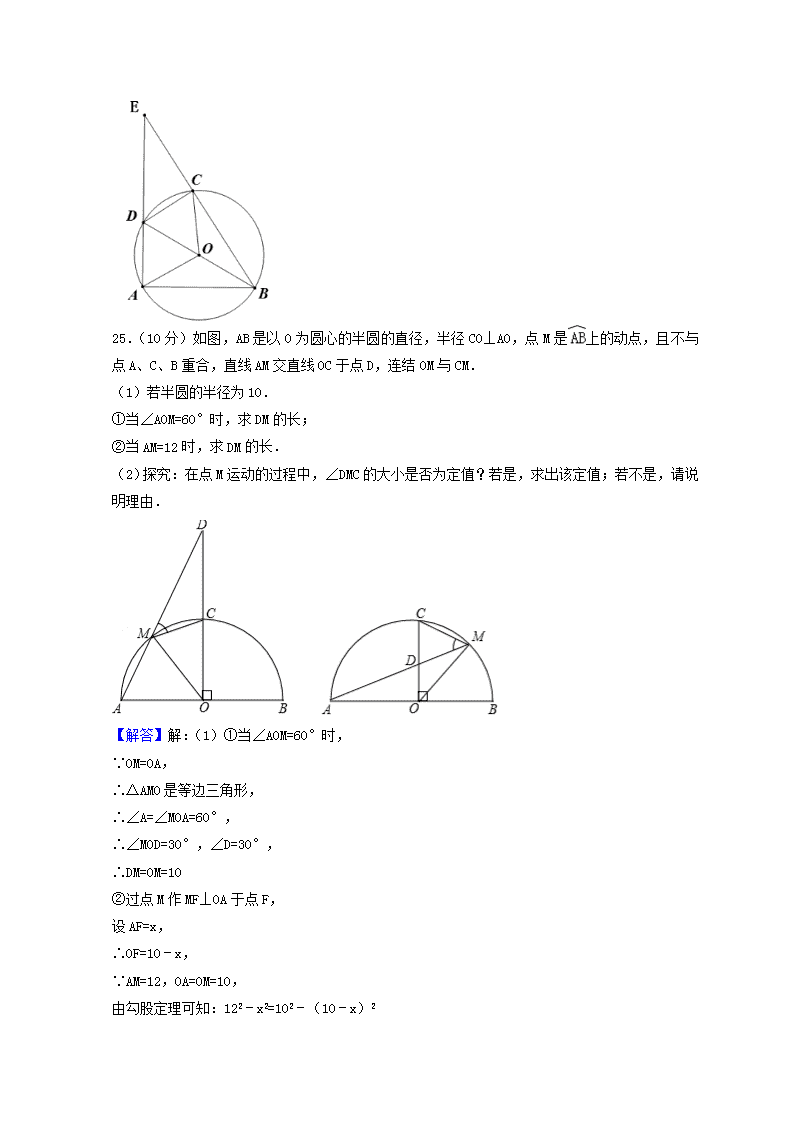
25.(10 分)如图,AB 是以 O 为圆心的半圆的直径,半径 CO⊥AO,点 M 是 上的动点,且不与
点 A、C、B 重合,直线 AM 交直线 OC 于点 D,连结 OM 与 CM.
(1)若半圆的半径为 10.
①当∠AOM=60°时,求 DM 的长;
②当 AM=12 时,求 DM 的长.
(2)探究:在点 M 运动的过程中,∠DMC 的大小是否为定值?若是,求出该定值;若不是,请说
明理由.
【解答】解:(1)①当∠AOM=60°时,
∵OM=OA,
∴△AMO 是等边三角形,
∴∠A=∠MOA=60°,
∴∠MOD=30°,∠D=30°,
∴DM=OM=10
②过点 M 作 MF⊥OA 于点 F,
设 AF=x,
∴OF=10﹣x,
∵AM=12,OA=OM=10,
由勾股定理可知:122﹣x2=102﹣(10﹣x)2
∴x= ,
∴AF= ,
∵MF∥OD,
∴△AMF∽△ADO,
∴ ,
∴ ,
∴AD=
∴MD=AD﹣AM=
(2)当点 M 位于 之间时,
连接 BC,
∵C 是 的重点,
∴∠B=45°,
∵四边形 AMCB 是圆内接四边形,
此时∠CMD=∠B=45°,
当点 M 位于 之间时,
连接 BC,
由圆周角定理可知:∠CMD=∠B=45°
综上所述,∠CMD=45°
(2018 温州)22.(本题 10 分)如图,D 是△ABC 的 BC 边上一点,连接 AD,作△ABD 的外接圆,
将△ADC 沿直线 AD 折叠,点 C 的对应点 E 落在上.
(1)求证:AE=AB.
(2)若∠CAB=90°,cos∠ADB= 1
3
,BE=2,求 BC 的长.
(2018 台州)24.如图, ABC 是 O 的内接三角形,点 D 在 BC 上,点 E 在弦 AB 上( E 不
与 A 重合),且四边形 BDCE 为菱形.
(1)求证: AC CE ;
(2)求证: 2 2BC AC AB AC ;
(3)已知 O 的半径为 3.
①若 5
3
AB
AC
,求 BC 的长;
②当 AB
AC
为何值时, AB AC 的值最大?
(2018 南通)28.如图, O 的直径 26AB ,P 是 AB 上(不与点 A B、 重合)的任一点,点 C D、
为 O 上的两点.若 APD BPC ,则称 CPD 为直径 AB 的“回旋角”.
(1)若 60BPC DPC ,则 CPD 是直径 AB 的 “回旋角”吗?并说明理由;
(2)若 CD 的长为 13
4
,求“回旋角” CPD 的度数;
(3)若直径 AB 的“回旋角”为120 ,且 PCD 的周长为 24 13 3 ,直接写出 AP 的长.
解:28.(1)是;
(2)45°;
(3)3 或 23.
(2018 湘潭)
(2018 南京)26.如图,在正方形 ABCD 中,E 是 AB 上一点,连接 DE .过点 A 作 AF DE ,
垂足为 F . O 经过点C 、 D 、 F ,与 AD 相交于点G .
(1)求证 AFG DFC∽△ △ ;
( 2 ) 若 正 方 形 ABCD 的 边 长 为 4 , 1AE , 求 O 的 半 径
(2018 黄冈)18. 如图, AD 是 O 的直径, AB 为 O 的弦,OP AD ,OP 与 AB 的延长
线交于点 P ,过 B 点的切线交OP 于点 C .
(1)求证: CBP ADB .
(2)若 2OA , 1AB ,求线段 BP 的长.
(2018 宜昌)21. 如图,在 ABC 中,AB AC . 以 AB 为直径的半圆交 AC 于点 D ,交 BC
于点 E .延长 AE 至点 F,使 EF AE ,连接 FB FC, .
(1)求证:四边形 ABFC 是菱形;
(2) 若 AD 7 BE 2 , ,求半圆和菱形 ABFC 的面积.
21.(1)证明: AB 为半圆的直径,
90AEB ,
AB AC ,
CE BE ,
又 EF AE ,
∴四边形 ABFC 是平行四边形.
又 AB AC ,(或 90AEB ,)
∴平行四边形 ABFC 是菱形.
(2)解:∵ 7, 2AD BE CE ,
设CD x ,则 7AB AC x ,
解法一:连接 BD ,(如图)
图 1
∵ AB 为半圆的直径,
90ADB ,
2 2 2 2AB AD CB CD
2 2 2 2(7 ) 7 4x x
1 1x 或 2 8x (舍去)
解法二:连接 DE .(如图)
图 2
∵四边形 ABED 是圆内接四边形
180ADE ABC
180ADE CDE
CDE ABE
DCE BCA
CDE CBA ∽
CD CB
CE CA
4
2 7
x
x
2 7 8 0x x
1 1x 或 2 8x (舍去)
解法三:如图 1,连接 BD ,
AB 为半径的直径,
90ADB
可证 CDB CEA ∽
CD CB
CE CA
4
2 7
x
x
1 1x 或 2 8x (舍去)
21= 4 =82S 半圆
15BD ,
=8 15S 菱形
(2018 福建)
(2018 张家界)20、(本小题满分 6 分)
如图,点 P 是⊙O 的直径 AB 延长线上一点,且 AB =4,点 M 为 上一个动点(不与 BA、
重合),射线 PM 与⊙O 交于点 N (不与 M 重合)
(1) 当 M 在什么位置时, MAB 的面积最大,并求岀这个最大值;
(2)求证: PAN ∽ PMB .
20.解:(1)当点 M 在 AB 弧的中点处时, 最大 ………………1 分
(其它表述合理均给分)
因为此时:
242
1
2
1 ABOM
………………2 分
4242
1
2
1 OMABS ABM
……………3 分
(2) PANPMB …………4 分
PP …………5 分
PMB∽ PAM …………6 分
(2018 贵阳)
23.(本题满分 10 分)如图,AB 为⊙ O 的直径,,,且,AB 4 ,点 C 在半圆上,OC AB , 垂足为点O ,P
为半圆上任意一点,过 P 点作 PE OC 于点 E,设 OPE 的内心
为 M ,连接OM、PM .
(1)求 OMP 的度数;
(2)当点 P 在半圆上从点 B 运动到点 A 时,求内心 M 所经过的路径长.
ABMS
【解】(1)∵ PE OC ∴ PEO
90
∴ EPO EOP 90
∵ M 是 OPE 的内心 ∴ EOM POM, EPM OPM
∴ POM OPM 1 ( EPO EOP) 45
2
在 POM 中, OMP 180 ( POM OPM ) 180 45 135
(2)连接CM ,作过O、M、C 三点的外接圆,即⊙ N ,连接 NC、NO ,在⊙ N
的优弧上任取一点 H ,连接 HC、HO .如图所示:
由题意知:OP OC, POM COM,OM OM
∴ POM ≌ COM
∴ OMP OMC 135
在⊙ N 的内接四边形CMOH 中, H 180 OMC 180 135 45
∴ N 2 45 90
由题意知:OC 1 AB 1 4 2
2 2
在等腰直角三角形CNO 中, NC NO
由勾股定理得: NC 2 NO 2 OC 2 即 2 NC 2 22 NC 2
当点 P 在 上运动时,点 M 在 上运动
90∴ 的长为:
180
∵ 与 关于 OC 对称
2 2
2
∴当点 P 在 上运动时,点 M 所在弧上的运动路径长与当点 P 在 上运动时,点 M 在
上运动的路径长相等
∴当点 P 在半圆上从点 B 运动到点 A 时,求内心 M 所经过的路径长为:
2 2 2
2
(2018 遵义)
25. (12 分)如图,AB 是半圆O 的直径,C是AB 延长线上的点,AC 的垂直平分线交半圆于点
D,交 AC 于点 E,连接 DA,DC.已知半圆 0 的半径为 3,BC=2.
(1) 求AD 的长.
(2) 点P 是线段AC 上一动点,连接 DP,作∠DPF=∠DAC,PF 交线段CD 于点F.当∆DPF 为等腰三角形时,求 AP 的长.
(2018 哈尔滨)
类型 2 与切线有关的计算与证明
(2018 十堰)23.如图, ABC 中, AB AC ,以 AB 为直径的 O 交 BC 于点 D ,交 AC 于点 E ,过点 D 作
FG AC 于点 F ,交 AB 的延长线于点G .
(1)求证: FG 是 O 的切线;
(2)若 tan 2C ,求 GB
GA
的值.
(2018·德州)22.如图, AB 是 O 的直径,直线CD 与 O 相切于点C ,且与 AB 的延长线交于点 E .点C 是 BF 的
中点.
(1)求证: AD CD
(2)若 30CAD . O 的半径为 3,一只蚂蚁从点 B 出发,沿着 BE CEC B 爬回至点 B ,求蚂蚁爬过的路程
3.14 3 1.73 , 结果保留一位小数.
(2018·绵阳)如图,AB 是 O 的直径,点 D 在 O 上(点 D 不与 A,B 重合),直线 AD 交过点 B 的切线于点 C,
过点 D 作 O 的切线 DE 交 BC 于点 E。
(1)求证:BE=CE;
(2)若 DE 平行 AB,求 ACOsin 的值。
(2018·滨州)22.如图,AB 为 O 的直径,点C 在 O 上, AD CD 于点 D ,且 AC 平分 DAB .求证;(1)直线
DC 是 O 的切线;(2) 2 2AC AD AO .
(2018 内江)26.如图,以 Rt ABC 的直角边 AB 为直径作 O 交斜边 AC 于点 D ,过圆心O 作 / /OE AC ,交 BC
于点 E ,连接 DE .
(1)判断 DE 与 O 的位置关系并说明理由;
(2)求证: 22DE CD OE ;
(3)若 4tan 3C , 5
2DE ,求 AD 的长.
(2018•内江)如图,以 Rt△ABC 的直角边 AB 为直径作⊙O 交斜边 AC 于点 D,过圆心 O 作 OE∥AC,交 BC 于点 E,
连接 DE.
(1)判断 DE 与⊙O 的位置关系并说明理由;
(2)求证:2DE2=CD•OE;
(3)若 tanC= ,DE= ,求 AD 的长.
【解答】解:(1)DE 是⊙O 的切线,理由:如图,
连接 OD,BD,∵AB 是⊙O 的直径,
∴∠ADB=∠BDC=90°,
∵OE∥AC,OA=OB,
∴BE=CE,
∴DE=BE=CE,
∴∠DBE=∠BDE,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODE=∠OBE=90°,
∵点 D 在⊙O 上,
∴DE 是⊙O 的切线;
(2)∵∠BCD=∠ABC=90°,∠C=∠C,
∴△BCD∽△ACB,
∴ ,
∴BC2=CD•AC,
由(1)知 DE=BE=CE= BC,
∴4DE2=CD•AC,
由(1)知,OE 是△ABC 是中位线,
∴AC=2OE,
∴4DE2=CD•2OE,
∴2DE2=CD•OE;
(3)∵DE= ,
∴BC=5,
在 Rt△BCD 中,tanC= = ,
设 CD=3x,BD=4x,根据勾股定理得,(3x)2+(4x)2=25,
∴x=﹣1(舍)或 x=1,
∴BD=4,CD=3,
由(2)知,BC2=CD•AC,
∴AC= = ,
∴AD=AC﹣CD= ﹣3= .
(2018·甘肃)
(2018·南充)22.如图,C 是 O 上一点,点 P 在直径 AB 的延长线上, O 的半径为 3, 2PB , 4PC .
(1)求证: PC 是 O 的切线.
(2)求 tan CAB 的值.
22.解:(1)证明:连接 OC .
∵ O 的半径为 3,∴ 3OC OB .
又∵ 2BP ,∴ 5OP .
在 OCP 中, 2 2 2 2 2 23 4 5OC PC OP ,
∴ OCP 为直角三角形, 90OCP .
∴OC PC ,故 PC 为 O 的切线.
(2)过C 作CD OP 于点 D , 90ODC OCP .
∵ COD POC ,∴ OCD OPC .
∴ OC OP PC
OD OC CD
,∴ 2OC OD OP ,∴
2 9
5
OCOD OP
, 4 5
3DC
,∴ 12
5CD .
又∵ 24
5AD OA OD ,
∴在 Rt CAD 中, 1tan 2
CDCAB AD
.
(2018·金华/丽水)如图,在 Rt△ABC 中,点 O 在斜边 AB 上,以 O 为圆心,OB 为半径作圆,分别与 BC,AB 相交于
点 D,E,连结 AD.已知∠CAD=∠B.
(1)求证:AD 是⊙O 的切线.
(2)若 BC=8,tanB= 1
2
,求⊙O 的半径.
(2018 宁波)
(2018 衢州)如图,已知 AB 为⊙O 直径,AC 是⊙O 的切线,连接 BC 交⊙O 于点 F,取弧 BF 的中点 D,连接 AD 交
BC 于点 E,过点 E 作 EF⊥AB 于 H。
(1)求证:△HBE∽△ABC;
(2)若 CF=4,BF=5,求 AC 和 EH 的长。
(2018·枣庄)23.如图,在 Rt ACB 中, 090C , cmBCcmAC 4,3 ,以 BC 为直径作⊙O 交 AB 于
点 D .
(1)求线段 AD 的长度;
(2)点 F 是线段 AC 上的一点,试问:当点 E 在什么位置时,直线 ED 与⊙O 相切?请说明理由.
解:(1)在 Rt△ACB 中,∵AC=3cm,BC=4cm,∠ACB=90°,∴AB=5cm;
连接 CD,∵BC 为直径,
∴∠ADC=∠BDC=90°;
∵∠A=∠A,∠ADC=∠ACB,
∴Rt△ADC∽Rt△ACB;
∴ ,∴ ;
(2)当点 E 是 AC 的中点时,ED 与⊙O 相切;
证明:连接 OD,
∵DE 是 Rt△ADC 的中线;
∴ED=EC,
∴∠EDC=∠ECD;
∵OC=OD,
∴∠ODC=∠OCD;
∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°;
∴ED⊥OD,
∴ED 与⊙O 相切.
(2018 成都)20.如图,在 Rt ABC 中, 90C ,AD 平分 BAC 交 BC 于点 D ,O 为 AB 上一点,经过点 A ,
D 的 O⊙ 分别交 AB , AC 于点 E , F ,连接OF 交 AD 于点G .
(1)求证: BC 是 O⊙ 的切线;
(2)设 AB x , AF y ,试用含 ,x y 的代数式表示线段 AD 的长;
(3)若 8BE , 5sin 13B ,求 DG 的长.
23.(10 分)(2018•自贡)如图,在△ABC 中,∠ACB=90°.
(1)作出经过点 B,圆心 O 在斜边 AB 上且与边 AC 相切于点 E 的⊙O(要求:用尺规作图,保留作图痕迹,不写作
法和证明)
(2)设(1)中所作的⊙O 与边 AB 交于异于点 B 的另外一点 D,若⊙O 的直径为 5,BC=4;求 DE 的长.(如果用尺
规作图画不出图形,可画出草图完成(2)问)
解:(1)⊙O 如图所示;
(2)作 OH⊥BC 于 H.
∵AC 是⊙O 的切线,
∴OE⊥AC,
∴∠C=∠CEO=∠OHC=90°,
∴四边形 ECHO 是矩形,
∴OE=CH= ,BH=BC﹣CH= ,
在 Rt△OBH 中,OH= =2,
∴EC=OH=2,BE= =2 ,
∵∠EBC=∠EBD,∠BED=∠C=90°,
∴△BCE∽△BED,
∴ = ,
∴ = ,
∴DE= .
(2018 泸州)24.如图 10,已知 AB,CD 是⊙O 的直径,过点 C 作⊙O 的切线交 AB 的延长线于点 P,⊙O 的弦 DE 交
AB 于点 F,且 DF=EF.
(1)求证: 2CO OF OP ;
(2)连接 EB 交 CD 于点 G,过点 G 作 GH AB 于点 H,若 PC= 4 2 ,PB=4,求 GH 的长.
【解答】(1)证明:∵PC 是⊙O 的切线,
∴OC⊥PC,
∴∠PCO=90°,
∵AB 是直径,EF=FD,
∴AB⊥ED,
∴∠OFD=∠OCP=90°,
∵∠FOD=∠COP,
∴△OFD∽△OCP,
∴ = ,∵OD=OC,
∴OC2=OF•OP.
(2)解:如图作 CM⊥OP 于 M,连接 EC、EO.设 OC=OB=r.
在 Rt△POC 中,∵PC2+OC2=PO2,
∴(4 )2+r2=(r+4)2,
∴r=2,
∵CM= = ,
∵DC 是直径,
∴∠CEF=∠EFM=∠CMF=90°,
∴四边形 EFMC 是矩形,
∴EF=CM= ,
在 Rt△OEF 中,OF= = ,
∴EC=2OF= ,
∵EC∥OB,
∴ = = ,
∵GH∥CM,
∴ = = ,
∴GH= .
(2018 宜宾)23.(10 分)(2018•宜宾)如图,AB 为圆 O 的直径,C 为圆 O 上一点,D 为 BC 延长线一点,且 BC=CD,
CE⊥AD 于点 E.
(1)求证:直线 EC 为圆 O 的切线;
(2)设 BE 与圆 O 交于点 F,AF 的延长线与 CE 交于点 P,已知∠PCF=∠CBF,PC=5,PF=4,求 sin∠PEF 的值.
【解答】解:(1)证明:∵CE⊥AD 于点 E
∴∠DEC=90°,
∵BC=CD,
∴C 是 BD 的中点,又∵O 是 AB 的中点,
∴OC 是△BDA 的中位线,
∴OC∥AD
∴∠OCE=∠CED=90°
∴OC⊥CE,又∵点 C 在圆上,
∴CE 是圆 O 的切线.
(2)连接 AC
∵AB 是直径,点 F 在圆上
∴∠AFB=∠PFE=90°=∠CEA
∵∠EPF=∠EPA
∴△PEF∽△PEA
∴PE2=PF×PA
∵∠FBC=∠PCF=∠CAF
又∵∠CPF=∠CPA
∴△PCF∽△PAC
∴PC2=PF×PA
∴PE=PC
在直角△PEF 中,sin∠PEF= = .
(2018 衡阳)23.如图, O 是 ABC 的外接圆,AB 为直径, BAC 的平分线交 O 于点 D ,过点 D 作 DE AC
分别交 AC 、 AB 的延长线于点 E 、 F .
(1)求证: EF 是 O 的切线;
(2)若 4AC , 2CE ,求 BD 的长度.(结果保留 )
解:(1)如图,连接 OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD 平分∠EAF,
∴∠DAE=∠DAO,
∴∠DAE=∠ADO,
∴OD∥AE,
∵AE⊥EF,
∴OD⊥EF,
∴EF 是⊙O 的切线;
(2)如图,作 OG⊥AE 于点 G,连接 BD,
则 AG=CG= AC=2,∠OGE=∠E=∠ODE=90°,
∴四边形 ODEG 是矩形,
∴OA=OB=OD=CG+CE=2+2=4,∠DOG=90°,
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD,
∴ = ,即 = ,
∴AD2=48,
在 Rt△ABD 中,BD= =4,
在 Rt△ABD 中,∵AB=2BD,
∴∠BAD=30°,
∴∠BOD=60°,
则 的长度为 = .
(2018 聊城)
24.如图,在 Rt ABC 中, 90C ,BE 平分 ABC 交 AC 于点 E ,作 ED EB 交 AB 于点 D , O 是 BED
的外接圆.
(1)求证: AC 是 O 的切线;
(2)已知 O 的半径为 2.5, 4BE ,求 BC , AD 的长.
(2018 泰州)22.如图, AB 为 O☉ 的直径, C 为 O☉ 上一点, ABC∠ 的平分线交 O☉ 于点 D , DE BC 于点 E .
(1)试判断 DE 与 O☉ 的位置关系,并说明理由.
(2)过点 D 作 DF AB 于点 F ,若 3 3BE , 3DF ,求图中阴影部分的面积.
解:(1)DE 与⊙O 相切,
理由:连接 DO,
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC 的平分线交⊙O 于点 D,
∴∠EBD=∠DBO,
∴∠EBD=∠BDO,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE 与⊙O 相切;
(2)∵∠ABC 的平分线交⊙O 于点 D,DE⊥BE,DF⊥AB,
∴DE=DF=3,
∵BE=3 ,
∴BD= =6,
∵sin∠DBF= = ,
∴∠DBA=30°,
∴∠DOF=60°,
∴sin60°= = = ,
∴DO=2 ,
则 FO= ,
故图中阴影部分的面积为: ﹣ × ×3=2π﹣ .
(2018 白银、武威、张掖)20.如图,在 ABC 中, 90ABC .
(1)作 ACB 的平分线交 AB 边于点O ,再以点O 为圆心,OB 的长为半径作 O ;(要求:不写作法,保留作
图痕迹)
(2)判断(1)中 AC 与 O 的位置关系,直接写出结果.
20.解:(1)如图,作出角平分线 CO;
作出⊙O.
(2)AC 与⊙O 相切.
(2018 白银、武威、张掖)27.如图,点O 是 ABC 的边 AB 上一点, O 与边 AC 相切于点 E ,与边 BC , AB
分别相交于点 D , F ,且 DE EF .
(1)求证: 90C ;
(2)当 3BC , 3sin 5A 时,求 AF 的长.
27.(1)证明:连接 OE,BE.
∵ DE=EF,∴ DE︵=EF︵,∴ ∠OBE=∠DBE.
∵ OE=OB,∴∠OEB=∠OBE,
∴∠OEB =∠DBE,∴OE∥BC.
∵⊙O 与边 AC 相切于点 E,∴ OE⊥AC.
∴BC⊥AC,∴∠C=90°.
(2)解:在△ABC 中,∠C=90°,BC=3, 3sin 5A ,
∴AB=5.
设⊙O 的半径为 r,则 AO=5-r,
在 Rt △AOE 中, 3sin 5 5
OE rA OA r
,
∴ 15
8r .
∴ 15 55 2 8 4AF .
(2018 常德)24.如图 12,已知 O 是等边三角形 ABC 的外接圆,点 D 在圆上,在CD 的延长线上有一点 F ,使
DF DA , / /AE BC 交CF 于 E .
(1)求证: EA 是 O 的切线;
(2)求证: BD CF .
【解答】证明:(1)连接 OD,
∵⊙O 是等边三角形 ABC 的外接圆,
∴∠OAC=30°,∠BCA=60°,
∵AE∥BC,
∴∠EAC=∠BCA=60°,
∴∠OAE=∠OAC+∠EAC=30°+60°=90°,
∴AE 是⊙O 的切线;
(2)∵△ABC 是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
∵A、B、C、D 四点共圆,
∴∠ADF=∠ABC=60°,
∵AD=DF,
∴△ADF 是等边三角形,
∴AD=AF,∠DAF=60°,
∴∠BAC+∠CAD=∠DAF+∠CAD,
即∠BAF=∠CAF,
在△BAD 和△CAF 中,
∵ ,
∴△BAD≌△CAF,
∴BD=CF.
(2018 娄底)25.如图, C D、 是以 AB 为直径的 Oe 上的点, » »AC BC= ,弦 CD 交 AB 于点 E .
(1)当 PB是 Oe 的切线时,求证: PBD DABÐ = Ð ;
(2)求证: 2 2BC CE CE DE- = × ;
(3)已知 OA=4 , E 是半径 OA 的中点,求线段 DE 的长.
解:(1)∵AB 是⊙O 的直径,
∴∠ADB=90°,即∠BAD+∠ABD=90°,
∵PB 是⊙O 的切线,
∴∠ABP=90°,即∠PBD+∠ABD=90°,
∴∠BAD=∠PBD;
(2)∵∠A=∠C、∠AED=∠CEB,
∴△ADE∽△CBE,
∴ = ,即 DE•CE=AE•BE,
如图,连接 OC,
设圆的半径为 r,则 OA=OB=OC=r,
则 DE•CE=AE•BE=(OA﹣OE)(OB+OE)=r2﹣OE2,
∵ = ,
∴∠AOC=∠BOC=90°,
∴CE2=OE2+OC2=OE2+r2,BC2=BO2+CO2=2r2,
则 BC2﹣CE2=2r2﹣(OE2+r2)=r2﹣OE2,
∴BC2﹣CE2=DE•CE;
(3)∵OA=4,
∴OB=OC=OA=4,
∴BC= =4 ,
又∵E 是半径 OA 的中点,
∴AE=OE=2,
则 CE= = =2 ,
∵BC2﹣CE2=DE•CE,
∴(4 )2﹣(2 )2=DE•2 ,
解得:DE= .
(2018 永州)24.如图,线段 AB 为 O 的直径,点C 、 E 在 O 上, BC CE ,CD AB ,垂足为点 D ,连
接 BE ,弦 BE 与线段CD 相交于点 F .
(1)求证:CF BF ;
(2)若 4cos 5ABE ,在 AB 的延长线上取一点 M ,使 4BM , O 的半径为 6 ,求证:直线CM 是 O 的
切线.
25、(本题满分 10 分)如图,已知 AB 为⊙O 的直径,AB=8,点 C 和点 D 是⊙O 上关于直线 AB 对称的两个点,连接
OC、AC,且∠BOC<90°,直线 BC 和直线AD 相交于点 E,过点 C 作直线 CG 与线段 AB 的延长线相交于点 F,与直线
AD 相交于点 G,且∠GAF=∠GCE
(1)求证:直线 CG 为⊙O 的切线;
(2)若点 H 为线段 OB 上一点,连接 CH,满足 CB=CH,
①△CBH∽△OBC;
②求 OH+HC 的最大值.
(1)证明:∵C、D 关于 AB 对称
∴∠GAF=∠CAF
∵∠GAF=∠GCE,∴∠GCE=∠CAF
∵OA=OC,∴∠CAF=∠ACO,∴∠GCE=∠ACO
∵AB 为直径
∴∠ACO+∠OCB=90°
∴∠GCE+∠OCB=90°
即∠OCG=90°,∴CG 为圆 O 的切线.
(2)①∵OC=OB,CH=BC
∴∠OCB=∠OBC,∠CHB=∠CBH
∠CBH=∠OBC=∠OCB=∠CHB
△CBH∽△OBC
②
4,
2BCBMOB
BC
BC
BH
设 BC=x,则 CH=x,BH=
4
2x
524
144
1 22 xxxHCOH
∴当 x=2 时,最大值为 5.
(2018 宿迁)26. (本题满分 10 分)
如图,AB、AC 分别是 O 的直径和弦,OD⊥AC 于点 D,过点 A 作 O 的切线与 OD 的延长线交于点 P,PC、AB 的延长
线交于点 F.
⑴ 求证:PC 是 O 的切线;
⑵ 若∠ABC=600,AB=10,求线段 CF 的长,
(2018 盐城)25.如图,在以线段 AB 为直径的 O 上取一点,连接 AC 、BC .将 ABC 沿 AB 翻折后得到 ABD .
(1)试说明点 D 在 O 上;
(2)在线段 AD 的延长线上取一点 E ,使 2AB AC AE .求证: BE 为 O 的切线;
(3)在(2)的条件下,分别延长线段 AE 、CB 相交于点 F ,若 2BC , 4AC ,求线段 EF 的长.
(2018 扬州)25.如图,在 ABC 中, AB AC , AO BC 于点O ,OE AB 于点 E ,以点O 为圆心,OE 为
半径作半圆,交 AO 于点 F .
(1)求证: AC 是 O 的切线;
(2)若点 F 是 AO 的中点, 3OE ,求图中阴影部分的面积;
(3)在(2)的条件下,点 P 是 BC 边上的动点,当 PE PF 取最小值时,直接写出 BP 的长.
(1)证明:作 OH⊥AC 于 H,如图,
∵AB=AC,AO⊥BC 于点 O,
∴AO 平分∠BAC,
∵OE⊥AB,OH⊥AC,
∴OH=OE,
∴AC 是⊙O 的切线;
(2)解:∵点 F 是 AO 的中点,
∴AO=2OF=3,
而 OE=3,
∴∠OAE=30°,∠AOE=60°,
∴AE= OE=3 ,
∴图中阴影部分的面积=S△AOE﹣S 扇形 EOF= ×3×3 ﹣ = ;
(3)解:作 F 点关于 BC 的对称点 F′,连接 EF′交 BC 于 P,如图,
∵PF=PF′,
∴PE+PF=PE+PF′=EF′,此时 EP+FP 最小,
∵OF′=OF=OE,
∴∠F′=∠OEF′,
而∠AOE=∠F′+∠OEF′=60°,
∴∠F′=30°,
∴∠F′=∠EAF′,
∴EF′=EA=3 ,
即 PE+PF 最小值为 3 ,
在 Rt△OPF′中,OP= OF′= ,
在 Rt△ABO 中,OB= OA= ×6=2 ,
∴BP=2 ﹣ = ,
即当 PE+PF 取最小值时,BP 的长为 .
(2018 江西省卷)20.如图,在 ABC 中,O 为 AC 上一点,以点O 为圆心,OC 为半径作圆,与 BC 相切于点C ,
过点 A 作 AD BO 交 BO 的延长线于点 D ,且 AOD BAD .
(1)求证: AB 为 O 的切线;
(2)若 6BC , 4tan 3ABC ,求 AD 的长.
(2018 呼和浩特)
(2018 临沂)(2018•临沂)如图,△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D,OB 与⊙O
相交于点 E.
(1)求证:AC 是⊙O 的切线;
(2)若 BD= ,BE=1.求阴影部分的面积.
【解答】(1)证明:连接 OD,作 OF⊥AC 于 F,如图,
∵△ABC 为等腰三角形,O 是底边 BC 的中点,
∴AO⊥BC,AO 平分∠BAC,
∵AB 与⊙O 相切于点 D,
∴OD⊥AB,
而 OF⊥AC,
∴OF=OD,
∴AC 是⊙O 的切线;
(2)解:在 Rt△BOD 中,设⊙O 的半径为 r,则 OD=OE=r,
∴r2+( )2=(r+1)2,解得 r=1,
∴OD=1,OB=2,
∴∠B=30°,∠BOD=60°,
∴∠AOD=30°,
在 Rt△AOD 中,AD= OD= ,
∴阴影部分的面积=2S△AOD﹣S 扇形 DOF
=2× ×1× ﹣
= ﹣ .
(2018 潍坊)
22.如图, BD 为 ABC 外接圆 O 的直径,且 BAE C .
(1)求证: AE 与 O 相切于点 A ;
(2)若 , 2 7AE BC BC ∥ , 2 2AC ,求 AD 的长.
(2018 天津)21. 已知 AB 是 O 的直径,弦CD 与 AB 相交, 38BAC .
(Ⅰ)如图①,若 D 为 AB 的中点,求 ABC 和 ABD 的大小;
(Ⅱ)如图②,过点 D 作 O 的切线,与 AB 的延长线交于点 P ,若 / /DP AC ,求 OCD 的大小.
(2018 武汉)21.(本题 8 分)如图,PA 是⊙O 的切线,A 是切点,AC 是直径,AB 是弦,连接 PB、PC,PC 交 AB 于
点 E,且 PA=PB
(1) 求证:PB 是⊙O 的切线
(2) 若∠APC=3∠BPC,求
CE
PE 的值
(2018 邵阳)21.如图(十二)所示,AB 是⊙O 的直径,点 C 为⊙O 上一点,过点 B 作 BD⊥CD,
垂足为点 D,连结 BC.BC 平分∠ABD.
求证:CD 为⊙O 的切线.
21.(8 分)
证 明 : ∵ B C 平 分 ∠ A B D , ∴ ∠ O B C = ∠ D B C . … … … … … … … … … … … … … … … … … 2 分
∵ O B = O C , ∴ ∠ O B C = ∠ O C B . … … … … … … … … … … … … … … … … … … … … 4 分
∴ ∠ D B C = ∠ O C B . ∴ O C ∥ B D . … … … … … … … … … … … … … … … … … … … … 6 分
∵BD⊥CD,∴OC⊥CD.
又∵点 C 为⊙O 上一点,
∴CD 为⊙O 的切线.…………………………………………………………………8 分
(2018·淄博)22. (本小题满分 8 分)
如图,以 AB 为直径的 O 外接于 ABC ,过 A 点的切线 AP 与 BC 的延长线交于点 P , APB 的平分线分别交
,AB AC 于点 ,D E ,其中 ,AE BD AE BD 的长是一元二次方程 2 5 6 0x x 的两个实数根.
(1)求证: PA BD PB AE ;
(2)在线段 BC 上是否存在一点 M ,使得四边形 ADME 是菱形?若存在,请给予证明,并求其面积;若不存在,
说明理由.
解:(1)∵DP 平分∠APB,
∴∠APE=∠BPD,
∵AP 与⊙O 相切,
∴∠BAP=∠BAC+∠EAP=90°,
∵AB 是⊙O 的直径,
∴∠ACB=∠BAC+∠B=90°,
∴∠EAP=∠B,
∴△PAE∽△PBD,
∴ ,
∴PA•BD=PB•AE;
(2)过点 D 作 DF⊥PB 于点 F,作 DG⊥AC 于点 G,
∵DP 平分∠APB,
AD⊥AP,DF⊥PB,
∴AD=DF,
∵∠EAP=∠B,
∴∠APC=∠BAC,
易证:DF∥AC,
∴∠BDF=∠BAC,
由于 AE,BD(AE<BD)的长是 x2﹣5x+6=0,
解得:AE=2,BD=3,
∴由(1)可知: ,
∴cos∠APC= = ,
∴cos∠BDF=cos∠APC= ,
∴ ,
∴DF=2,
∴DF=AE,
∴四边形 ADFE 是平行四边形,
∵AD=AE,
∴四边形 ADFE 是菱形,
此时点 F 即为 M 点,
∵cos∠BAC=cos∠APC= ,
∴sin∠BAC= ,
∴ ,
∴DG= ,
∴在线段 BC 上是否存在一点 M,使得四边形 ADME 是菱形
其面积为:DG•AE=2× =
(2018 德阳)
(2018 广东省卷)24.如图,四边形 ABCD 中,AB=AD=CD,以 AB 为直径的⊙O 经过点 C,连接 AC、OD 交于点 E.
(1)证明:OD//BC;
(2)若 tan∠ABC=2,证明:DA 与⊙O 相切;
(3)在(2),连接 BD 交⊙O 于点 F,连接 EF,若 BC=1,求 EF 的长.
(2018 菏泽)22.如图, ABC 内接于 O , AB AC , 36BAC ,过点 A 作 / /AD BC ,与 ABC 的平分
线交于点 D , BD 与 AC 交于点 E ,与 O 交于点 F .
(1)求 DAF 的度数;
(2)求证: 2AE EF ED ;
(3)求证: AD 是 O 的切线.
(2018 随州)
(2018 咸宁)
(2018 孝感)23.如图, ABC 中, AB AC ,以 AB 为直径的 O 交 BC 于点 D ,交 AC 于点 E ,过点 D 作
DF AC 于点 F ,交 AB 的延长线于点G .
(1)求证: DF 是 O 的切线;
(2)已知 2 5BD , 2CF ,求 AE 和 BG 的长.
(2018 巴中)26. 已知如图 9 所示, ABC 中 30A B ,CD 是 ABC 的角平分线,以C 为圆心,CD 为
半径画圆,交CA 所在直线于 E 、 F 两点,连接 DE 、 DF .
(1)求证:直线 AB 是 C 的切线.
(2)若 10AC cm ,求 DF 的长
(2018 郴州)23.已知 BC 是 O 的直径,点 D 是 BC 延长线上一点,AB AD ,AE 是 O 的弦, 30AEC .
(1)求证:直线 AD 是 O 的切线;
(2)若 AE BC ,垂足为 M , O 的半径为 4 ,求 AE 的长.
(2018 深圳)22.如图 9,⊙ O 是 ABC 的外接圆, AB AC , 2BC , 10cos 10ABC 。点 D 为 AC 上的动点,
连接 AD 并延长,交 BC 的延长线于点 E 。
(1)试求 AB 的长;
(2)试判断 AD AE 的值是否为定值?若为定值,请求出这个定值,若不为定值,请说明理由。
(3)如图 10,连接 BD ,过点 A 作 AH ⊥ BD 于点 H ,连接CD ,求证: BH CD DH 。
22.解:(1)作 AM BC
, , 2AB AC AM BC BC
1 12BM CM BC
10cos 10
BMB AB
,在 Rt AMB 中, 1BM
10cos 1 1010AB BM B .
(2)连接 DC
AB AC
ACB ABC
∵四边形 ABCD 内接于圆O ,
图 10图 9
180ADC ABC ,
180ACE ACB ,
ADC ACE
CAE 公共
EAC CAD ∽
AC AE
AD AC
22 10 10AD AE AC .
(3)在 BD 上取一点 N ,使得 BN CD
在 ABN 和 ACD 中 3 1
AB AC
BN CD
( )ABN ACD SAS
AN AD
,AN AD AH BD
NH HD
,BN CD NH HD
BN NH CD HD BH .
(2018 黔东南、黔西南、黔南)22.如图,CE 是 O 的直径,BC 切 O 于点C ,连接 OB ,作 / /ED OB 交 O
于点 D , BD 的延长线与CE 的延长线交于点 A .
(1)求证: AB 是 O 的切线;
(2)若 O 的半径为1, tan 2DEO , 1tan 4A ,求 AE 的长.
(2018 恩施)23.如图, AB 为 O 直径, P 点为半径 OA 上异于O 点和 A 点的一个点,过 P 点作与直径 AB 垂直
的弦CD ,连接 AD ,作 BE AB , / /OE AD 交 BE 于 E 点,连接 AE 、 DE 、 AE 交CD 于 F 点.
(1)求证: DE 为 O 切线;
(2)若 O 的半径为3 , 1sin 3ADP ,求 AD ;
(3)请猜想 PF 与 FD 的数量关系,并加以证明.
23.(10 分)(2018•恩施州)如图,AB 为⊙O 直径,P 点为半径 OA 上异于 O 点和 A 点的一个点,过 P 点作与直径 AB
垂直的弦 CD,连接 AD,作 BE⊥AB,OE∥AD 交 BE 于 E 点,连接 AE、DE、AE 交 CD 于 F 点.
(1)求证:DE 为⊙O 切线;
(2)若⊙O 的半径为 3,sin∠ADP= ,求 AD;
(3)请猜想 PF 与 FD 的数量关系,并加以证明.
【解答】证明:(1)如图 1,连接 OD、BD,BD 交 OE 于 M,
∵AB 是⊙O 的直径,
∴∠ADB=90°,AD⊥BD,
∵OE∥AD,
∴OE⊥BD,
∴BM=DM,
∵OB=OD,
∴∠BOM=∠DOM,
∵OE=OE,
∴△BOE≌△DOE(SAS),
∴∠ODE=∠OBE=90°,
∴DE 为⊙O 切线;
(2)设 AP=a,
∵sin∠ADP= = ,
∴AD=3a,
∴PD= = =2 a,
∵OP=3﹣a,
∴OD2=OP2+PD2,
∴32=(3﹣a)2+(2 a)2,
9=9﹣6a+a2+8a2,
a1= ,a2=0(舍),
当 a= 时,AD=3a=2,
∴AD=2;
(3)PF=FD,
理由是:∵∠APD=∠ABE=90°,∠PAD=∠BAE,
∴△APF∽△ABE,
∴ ,
∴PF= ,
∵OE∥AD,
∴∠BOE=∠PAD,
∵∠OBE=∠APD=90°,
∴△ADP∽△OEB,
∴ ,
∴PD= ,
∵AB=2OB,
∴PD=2PF,
∴PF=FD.
(2018 黄石)21、(本小题 8 分)如图,已知 A、B、C、D、E 是⊙O 上五点,⊙O 的直径 2 3BE ,∠BCD=120°,
A 为 BE 的中点,延长 BA 到点 P,使 BA=AP,连接 PE
(1)求线段 BD 的长
(2)求证:直线 PE 是⊙O 的切线.
(2018 荆门)23.如图,AB 为 O 的直径,C 为 O 上一点,经过点C 的切线交 AB 的延长线于点 E ,AD EC
交 EC 的延长线于点 D , AD 交 O 于 F , FM AB 于 H ,分别交 O 、 AC 于 M 、 N ,连接 MB , BC .
(1)求证: AC 平方 DAE ;
(2)若 4cos 5M , 1BE ,①求 O 的半径;②求 FN 的长.
23.(1)证明:连接 OC ,
∵直线 DE 与 O 相切于点C ,
∴OC DE ,
又∵ AD DE ,∴ / /OC AD .
∴ 1 3
∵OA OC ,∴ 2 3 ,
∴ 1 2 ,
∴ AC 平方 DAE .
(2)解:①∵ BF BF ,∴ DAE M
又∵ / /OC AD ,∴ COE DAE M ,
∵OC DE ,∴ 90OCE
设 O 的半径为 r ,
则 4cos 1 5
OC OC rOCE OE OB OE r
,解得 4r
②连接 BF ,
∵ AB 为 O 的直径,∴ 90AFB ,∴ 4 32cos 8 5 5AF AB DAE ,
在 Rt OCE 中, 4 1 5OE r BE , 4OC ,∴ 2 2 2 25 4 3CE OE OC ,
∵ AB 为 O 的直径,∴ 2 90OBC ,
∵ 90OCE ,∴ 90OCB BCE ,
∵OB OC ,∴ OBC OCB ,∴ 2 1BCE ,
∵ AB FM ,∴ AM AF ,∴ 5 4 ,
∵ 90AFB D ,∴ / /FB DE ,∴ 5 4E ,
∴ AFN CEB ∽ ,
∴ AF FN
CE BE
,∴
32
325
3 15
AF BEFN CE
.
(2018 淮安)24.(本题满分 10 分)
如图,AB 是⊙O 的直径,AC 是⊙O 的切线,切点为 A,BC 交⊙O 于点 D,点 E 是 AC 的中点.
(1)试判断直线 DE 与⊙O 的位置关系,并说明理由;
(2)若⊙O 的半径为 2,∠B=50°,AC=4.8,求图中阴影部分的面积.
(1)先根据“SSS”证明△AEO≌△DEO,从而得到∠ODE=∠OAE=90°,即可判断出直线 DE 与⊙O 相切;
(2)阴影部分面积为: 24 10
5 9
.
22.(12 分)(2018 建设兵团)如图,PA 与⊙O 相切于点 A,过点 A 作 AB⊥OP,垂足为 C,交⊙O 于点 B.连接 PB,
AO,并延长 AO 交⊙O 于点 D,与 PB 的延长线交于点 E.
(1)求证:PB 是⊙O 的切线;
(2)若 OC=3,AC=4,求 sinE 的值.
(2018 河北)25. 如图 15,点 在数轴上对应的数为 26,以原点 为圆心, 为半径作优弧 ,使点 在
右下方,且 .在优弧 上任取一点 ,且能过 作直线 交数轴于点 ,设 在数轴上对
应的数为 ,连接 .
(1)若优弧 上一段 的长为 ,求 的度数及 的值;
(2)求 的最小值,并指出此时直线与 所在圆的位置关系;
(3)若线段 的长为 ,直接..写出这时 的值.
(2018 北京)22. 如图,AB 是⊙O 的直径,过⊙O 外一点 P 作⊙O 的两条切线 PC,PD,切点分别为 C,D,连接 OP,
CD.
(1)求证:OP⊥CD;
(2)连接 AD,BC,若∠DAB=50°,∠CBA = 70°,OA=2,求 OP 的长.
(2018 安顺)
25.如图,在 ABC 中, AB AC ,O 为 BC 的中点, AC 与半圆O 相切于点 D .
(1)求证: AB 是半圆O 所在圆的切线;
(2)若 2cos 3ABC , 12AB ,求半圆O 所在圆的半径.
(2018 遂宁)如图,过⊙O 外一点 P 作⊙O 的切线 PA 切⊙O 于点 A,连接 PO 并延长,与⊙O 交于 C、D 两点,M 是半
圆 CD 的中点,连接 AM 交 CD 于点 N,连接 AC、CM。
(1)求证:CM2=MN•MA
(2)若∠P=300,PC=2,求 CM 的长
(2018 仙桃)22.(满分 8 分)
如图,在⊙O 中,AB 为直径,AC 为弦.过 BC 延长线上一点 G,作 GD⊥AO 于点 D,交 AC 于点 E,交⊙O 于点 F,
M 是 GE 的中点,连接 CF,CM.
(1)判断 CM 与⊙O 的位置关系,并说明理由;
(2)若∠ECF 2∠A,CM 6,CF 4,求 MF 的长.
(第 22 题图)
·
A
B
C
DEFMG
O
(2018 玉林)
(2018 河南)19.(9 分)如图,AB 是圆 0 的直径,DO 垂直于点 O,连接 DA 交圆 O 于点 C,过点 C 作圆 O 的切线交
DO 于点 E,连接 BC 交 DO 于点 F。
(1)求证:CE=EF;
(2)连接 AF 并延长,交圆 O 于点 G,填空:
①当∠D 的度数为______时,四边形 ECFG 为菱形;
②当∠D 的度数为______时,四边形 ECOG 为正方形。
(2018 广西北部湾经济区)
(2018 兰州)
(2018 齐齐哈尔)
(2018 大庆)
(2018 怀化)
(2018陕西)23.(本题满分8分)
如图,在 Rt△ABC 中,∠ACB=90°,以斜边 AB 上的中线 CD 为直径作⊙O,分别与 AC、BC 相交于点 M、N.
(1)过点 N 作⊙O 的切线 NE 与 AB 相交于点 E,求证:NE⊥AB;
(2)连接 MD,求证:MD=NB.
23 题图 23 题解图(1)
解:(1)如图,连接 ON
∵CD 是 Rt△ABC 斜边 AB 上的中线
∴AD=CD=DB
∴∠DCB=∠DBC
又∵∠DCB=∠ONC
∴∠ONC=∠DBC
∴ON∥AB
∵NE 是⊙O 的切线,ON 是⊙O 的半径
∴∠ONE=90°
∴∠NEB=90°,即 NE⊥AB;
(2)如解图(1)所示,由(1)可知 ON∥AB,
O 为⊙O 的圆心,∴OC=OB,∠CMD=90°
∴CN=NB=1
2
CB,MD∥CB
又∵D 是 AB 的中点,∴MD=1
2
CB
∴MD=NB.
(2018 长春)
(2018 沈阳)
(2018 东营)22.(本题满分 8 分)如图,CD 是⊙O 的切线,点 C 在直径 AB 的延长线上.
(1)求证:∠CAD=∠BDC;
(2)若 BD=
3
2 AD,AC=3,求 CD 的长.
22.(本题满分 8 分)
(1)证明:连接 OD
∵OB=OD
∴∠OBD=∠ODB…………………………1 分
∵CD 是⊙O 的切线,OD 是⊙O 的半径
∴∠ODB+∠BDC=90°……………………2 分
∵AB 是⊙O 的直径
∴∠ADB=90°
∴∠OBD +∠CAD = 90°………………………………………3 分
∴∠CAD=∠BDC………………………………………………4 分
(2)解:∵∠C=∠C,∠CAD=∠BDC
∴△CDB ∽ △CAD………………………………………………5 分
∴
AC
CD
AD
BD …………………………………………………6 分
∵
3
2
AD
BD
∴
3
2
AC
CD …………………………………………………7 分
∵ AC=3
∴ CD=2…………………………………………………8 分
(2018 烟台)
(2018 陕西)
(2018 南京)27.结果如此巧合!
下面是小颖对一道题目的解答.
题目:如图, Rt ABC△ 的内切圆与斜边 AB 相切于点 D , 3AD , 4BD ,求 ABC△ 的面积.
解:设 ABC△ 的内切圆分别与 AC 、 BC 相切于点 E 、 F ,CE 的长为 x .
根据切线长定理,得 3AE AD , 4BF BD ,CF CE x .
根据勾股定理,得 2 2 23 4 3 4x x .
整理,得 2 7 12x x .
所以 1
2ABCS AC BC △
1 3 42 x x
21 7 122 x x
1 12 122
12 .
小颖发现12恰好就是3 4 ,即 ABC△ 的面积等于 AD 与 BD 的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知: ABC△ 的内切圆与 AB 相切于点 D , AD m , BD n .
可以一般化吗?
(1)若 90C ,求证: ABC△ 的面积等于 mn .
倒过来思考呢?
(2)若 2AC BC mn ,求证 90C .
改变一下条件……
(3)若 60C ,用 m 、 n 表示 ABC△ 的面积.
(2018 桂林)25.(本题满分 10 分)如图 1,已知⊙O 是ΔADB 的外接圆,∠ADB 的平分线 DC 交 AB 于点 M,交⊙O
于点 C,连接 AC,BC.
(1)求证:AC=BC;
(2)如图 2,在图 1 的基础上做⊙O 的直径 CF 交 AB 于点 E,连接 AF,过点 A 做⊙O 的切线 AH,若 AH//BC,求∠ACF
的度数;
(3)在(2)的条件下,若ΔABD 的面积为 36 ,ΔABD 与ΔABC 的面积比为 2:9,求 CD 的长.
25. (本题 10 分)
(1)∵DC 平 分 ∠ADB ∴∠ADC=∠BDC
∴AC=BC
(2)连接 AO 并延长交 BC 于 I 交⊙O 于 J
∵AH 是⊙O 的切线且 AH∥BC
∴AI⊥BC
∵垂径定理
∴BI=IC
∵AC=BC
∴IC=
2
1 AC
∴∠IAC=30°
∴∠ABC=60°=∠F=∠ACB
∵FC 是直径
∴∠FAC=90°
∴∠ACF=180°-90°-60°=30°
(3)过点 D 作 ABDG ,连接 AO
由(1)(2)知 ABC 为等边三角形
∵∠ACF=30°
∴ CFAB
∴AE=BE
∴ 3274
3 2
ΔABC ABS
∴AB= 36
∴ 33AE
在 RtΔAEO 中,设 EO=x,则 AO=2x
∴ 222 OEAEAO
∴ 222 )33()2( xx
∴x=6,⊙O 的半径为 6
∴CF=12
∵ 362
1362
1
ΔABD DGDGABS
∴DG=2
过点 D 作 CFDG ' ,连接 OD
∵ CFAB , ABDG
∴CF//DG
∴四边形 G’DGE 为矩形
∴ 2' EG
11236'' CEEGCG
在 RtΔ DOG' 中
6,5' ODOG
∴ 11' DG
∴ 3321111 22'2' CGDGCD
(2018 通辽)
(2018 昆明)
(2018 云南)
(2018 曲靖)
(2018 毕节)26.(本题 14 分)如图,在△ABC 中,以 BC 为直径的⊙O 交 AC 于点 E,过点 E 作 AB 的垂线交 AB 于点 F,
交 CB 的延长线于点 G,且∠ABG=2∠G.
(1)求证:EG 是⊙O 的切线;
(2)若
2
1tan C ,AC=8,求⊙O 的半径。
(2018 铜仁)
(2018 广安)
(2018 资阳)
(2018 苏州)
(2018 赤峰)
(2018 上海)