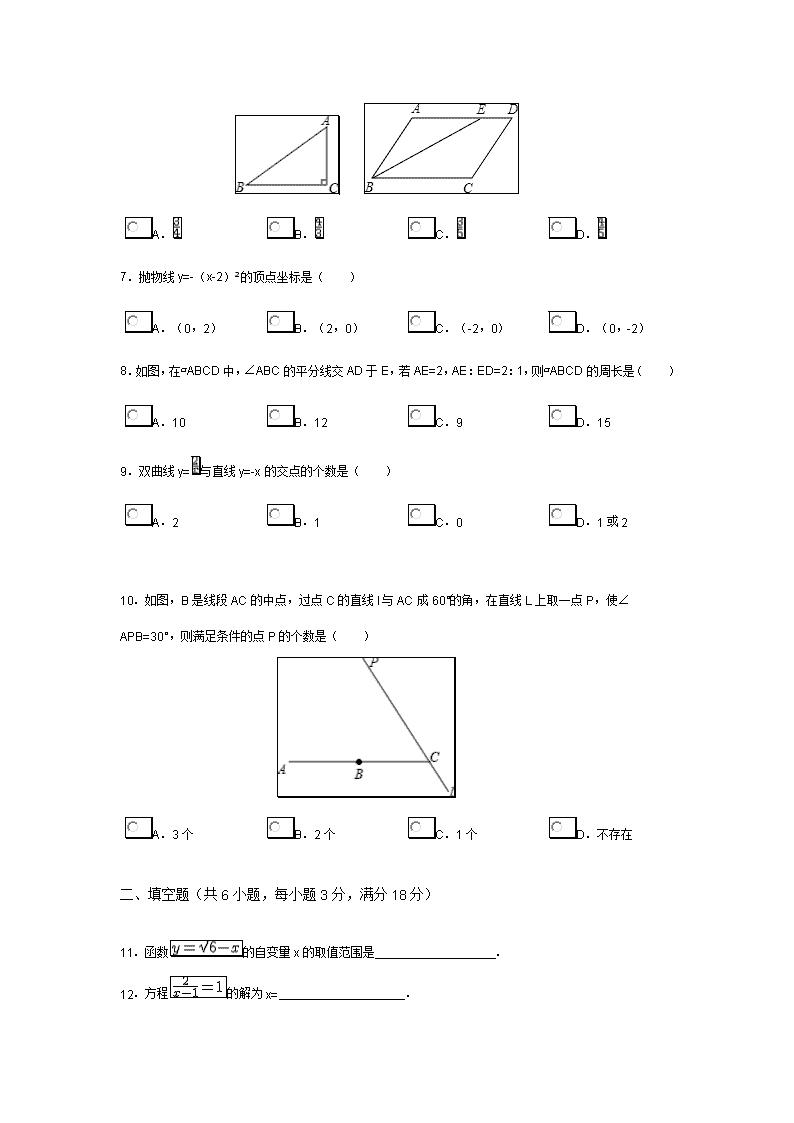广东省广州市天河区中考数学一模试卷 7页

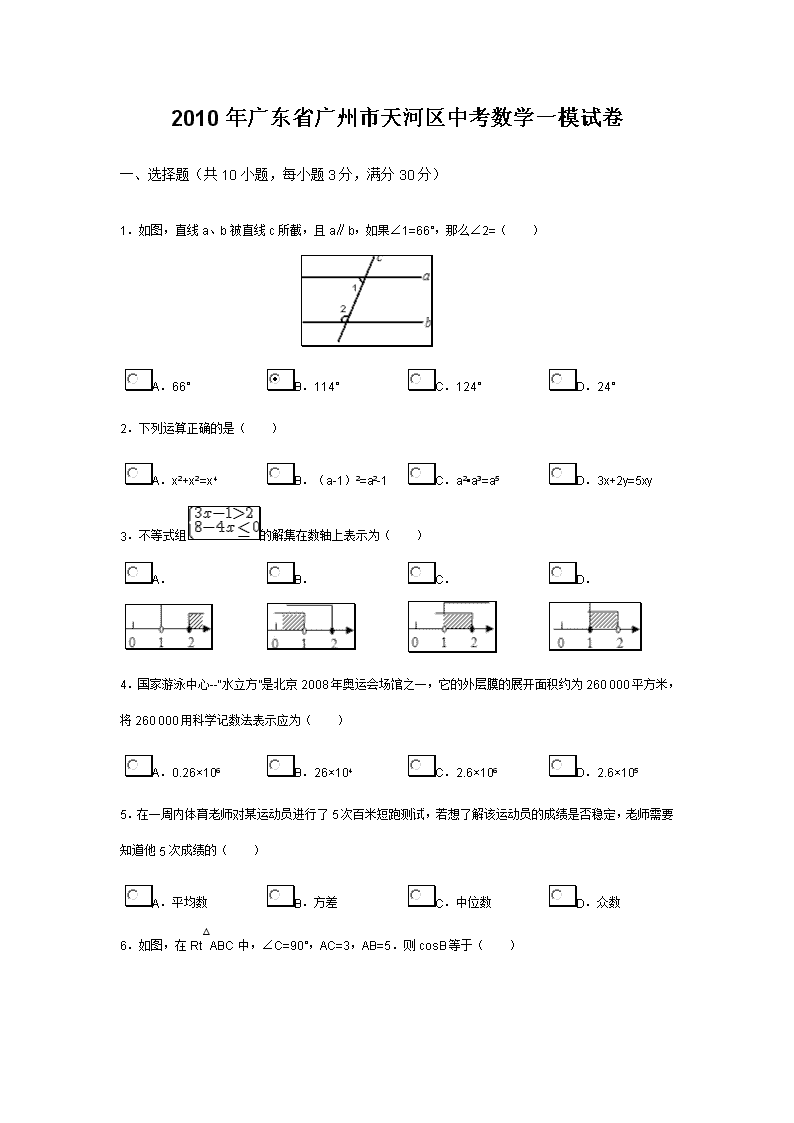
‎2010年广东省广州市天河区中考数学一模试卷 一、选择题（共10小题，每小题3分，满分30分）‎ ‎1．如图，直线a、b被直线c所截，且a∥b，如果∠1=66°，那么∠2=（　　）‎ ‎ ‎ A．66°‎ B．114°‎ C．124°‎ D．24°‎ ‎2．下列运算正确的是（　　）‎ A．x2+x2=x4‎ B．（a-1）2=a2-1‎ C．a2•a3=a5‎ D．3x+2y=5xy ‎3．不等式组的解集在数轴上表示为（　　）‎ A．‎ B．‎ C．‎ D．‎ ‎4．国家游泳中心--“水立方”是北京2008年奥运会场馆之一，它的外层膜的展开面积约为260 000平方米，将260 000用科学记数法表示应为（　　）‎ A．0.26×106‎ B．26×104‎ C．2.6×106‎ D．2.6×105‎ ‎5．在一周内体育老师对某运动员进行了5次百米短跑测试，若想了解该运动员的成绩是否稳定，老师需要知道他5次成绩的（　　）‎ A．平均数 B．方差 C．中位数 D．众数 ‎6．如图，在Rt△ABC中，∠C=90°，AC=3，AB=5．则cosB等于（　　）‎ ‎ ‎ A．‎ B．‎ C．‎ D．‎ ‎7．抛物线y=-（x-2）2的顶点坐标是（　　）‎ A．（0，2）‎ B．（2，0）‎ C．（-2，0）‎ D．（0，-2）‎ ‎8．如图，在▱ABCD中，∠ABC的平分线交AD于E，若AE=2，AE：ED=2：1，则▱ABCD的周长是（　　）‎ A．10‎ B．12‎ C．9‎ D．15‎ ‎9．双曲线y=与直线y=-x的交点的个数是（　　）‎ A．2‎ B．1‎ C．0‎ D．1或2‎ ‎10．如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线L上取一点P，使∠APB=30°，则满足条件的点P的个数是（　　）‎ ‎ ‎ A．3个 B．2个 C．1个 D．不存在 二、填空题（共6小题，每小题3分，满分18分）‎ ‎11．函数的自变量x的取值范围是 ．‎ ‎12．方程的解为x= ．‎ ‎13．一个圆锥的底面半径为3cm，高线长为4cm，则它的侧面积为 cm2．（结果保留π）‎ ‎14．某商店老板将一件进价为800元的商品先提价50%，再打8折卖出，则卖出这件商品所获利润 ‎ 是 元．‎ ‎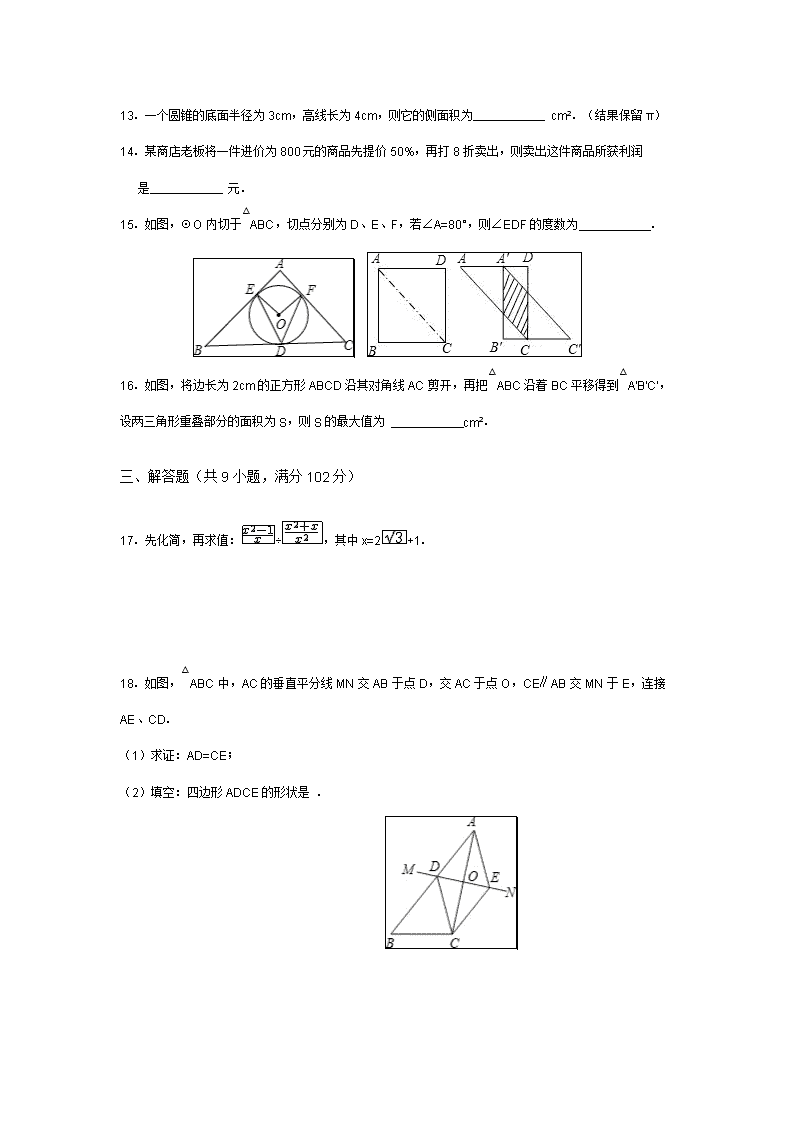15．如图，⊙O内切于△ABC，切点分别为D、E、F，若∠A=80°，则∠EDF的度数为 ．‎ ‎ ‎ ‎16．如图，将边长为2cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着BC平移得到△A′B′C′，设两三角形重叠部分的面积为S，则S的最大值为 cm2．‎ 三、解答题（共9小题，满分102分）‎ ‎17．先化简，再求值：÷，其中x=2+1．‎ ‎18．如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于E，连接AE、CD． （1）求证：AD=CE； （2）填空：四边形ADCE的形状是 ．‎ ‎ ‎ ‎19．一枚质量均匀的正方体骰子，六个面上分别标有数字1、2、3、4、5、6，抛掷这枚骰子两次．记第一次、第二次朝上的面上的数字分别为p、q，若把p，q分别作为点A的横坐标和纵坐标，用列表或树形图的方法求点A（p，q）在函数y=2x的图象上的概率．‎ ‎20．如图，在直角△ABC内，以A为一个顶点作正方形ADEF，使得点E落在BC边上． （1）用尺规作图，作出D、E、F中的任意一点（保留作图痕迹，不写作法和证明．另外两点不需要用尺规作图确定，作草图即可）； （2）若AB=6，AC=2，求正方形ADEF的边长．‎ ‎ ‎ ‎21．如图，已知一次函数y=kx+b（k≠0）的图象与反比例函数y=的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是-2． （1）一次函数的解析式； （2）△AOB的面积．‎ ‎ ‎ ‎22．团体购买公园门票票价如下：‎ 购票人数 ‎1～50‎ ‎51～100‎ ‎100人以上 每人门票（元）‎ ‎13元 ‎11元 ‎9元 今有甲、乙两个旅行团，已知甲团人数少于50人，乙团人数不超过100人．若分别购票，两团共计应付门票费1392元，若合在一起作为一个团体购票，总计应付门票费1080元． （1）请你判断乙团的人数是否也少于50人； （2）求甲、乙两旅行团各有多少人？‎ ‎23．如图，在Rt△ABC中，∠ACB=90°，AC=5，CB=12，AD是△ABC的角平分线，过A，C，D三点的圆与斜边AB交于点E，连接DE． （1）求证：AC=AE； （2）求△ACD外接圆的半径．‎ ‎24．如图，在直角坐标系中，以点A（，0）为圆心，以为半径的圆与x轴交于B、C两点，与y轴交于D、E两点． （1）求D点坐标． （2）若B、C、D三点在抛物线y=ax2+bx+c上，求这个抛物线的解析式． （3）若⊙A的切线交x轴正半轴于点M，交y轴负半轴于点N，切点为P，∠OMN=30°，试判断直线MN是否经过所求抛物线的顶点？说明理由．‎ ‎ ‎ ‎25．已知：如图①，在Rt△ACB中，∠C=90°，AC=4 cm，BC=3 cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题： （1）当t为何值时，PQ∥BC； （2）设△AQP的面积为y（cm2），求y与t之间的函数关系式； （3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由； （4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．‎ ‎ ‎