中考专题巧用对称解决线段的和差最值问题孙小林 4页

巧用对称解决线段的和差最值问题 基本图形一：分别在图1和图2上，在直线m上确定一点P，使得PA+PB最小 图1‎ 图2‎ ‎ ‎ 基本图形二．如图直线l上有固定长度的线段CD可以左右移动,直线上方有点A,点B,通过作图来说明,当CD在何处时,AC+CD+BD的和最小.(写出作图过程或步骤),通过作图来说明,当CD在何处时,AC+CD+BD的和最小.(简要写出作图过程或步骤)‎ 练习1:（2013日照）如图（a），点A、B在直线l的同侧，要在直线l上找一点C，使AC与BC的距离之和最小，我们可以作出点B关于l的对称点B′，连接AB′与直线l交于点C，则点C即为所求．‎ ‎（1）实践运用：‎ 如图（b），已知，⊙O的直径CD为4，点A在⊙O上，∠ACD=30°，B为弧AD的中点，P为直径CD上一动点，则BP+AP的最小值为　　　　　　．‎ ‎（2）知识拓展：‎ 如图（c），在Rt△ABC中，AB=10，∠BAC=45°，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，则BE+EF的最小值为：_______________‎ 练习2．（2011•咸宁）如图，在平面直角坐标系中，直线分别交x轴，y轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．‎ ‎（1）直接写出点A，B的坐标，并求直线AB与CD交点的坐标；‎ ‎②点Q是点B关于点A的对称点，问BP+PH+HQ是否有最小值？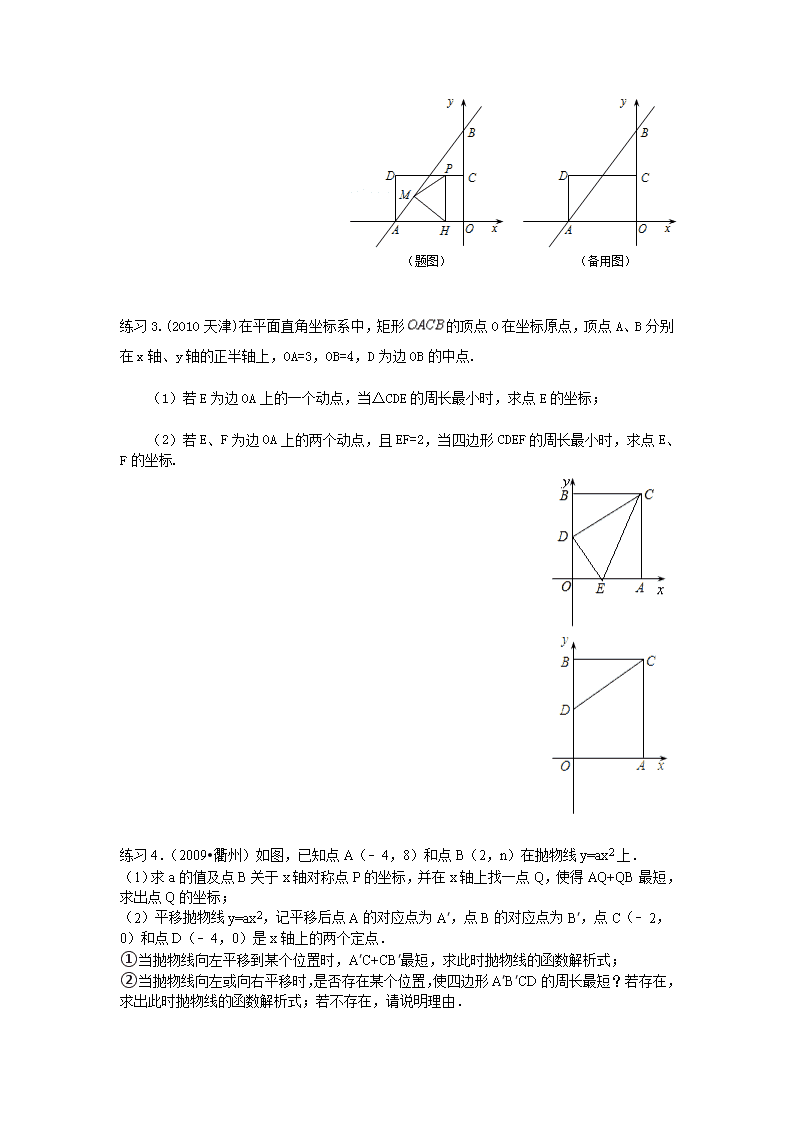如果有，求出相应的点P的坐标；如果没有，请说明理由．‎ 练习3.(2010天津)在平面直角坐标系中，矩形的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.‎ ‎ ‎ ‎（1）若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；‎ ‎ ‎ ‎（2）若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标.‎ 练习4．（2009•衢州）如图，已知点A（﹣4，8）和点B（2，n）在抛物线y=ax2上．‎ ‎（1）求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标；‎ ‎（2）平移抛物线y=ax2，记平移后点A的对应点为A′，点B的对应点为B′，点C（﹣2，0）和点D（﹣4，0）是x轴上的两个定点．‎ ‎①当抛物线向左平移到某个位置时，A′C+CB′最短，求此时抛物线的函数解析式；‎ ‎②当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．‎ 基本图形三：台球碰壁模型（光线照射模型）‎ 练习5如图，直线y=﹣x+5分别与x轴、y轴交于A、B两点．‎ ‎（1）求A、B两点的坐标；‎ ‎（2）已知点C坐标为（4，0），设点C关于直线AB的对称点为D，请直接写出点D的坐标:____________‎ ‎（3）请在直线AB和y轴上分别找一点M、N使△CMN的周长最短，在平面直角坐标系中作出图形，并求出点N的坐标．‎ 变题：‎ 直线AB的解析式分别与轴，轴交于两点，从点射出的光线经直线反射后再射到直线上，最后经直线反射后又回到点，则光线所经过的路程是____ ‎ 练习6.（2008•福州）如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．‎ ‎（1）直接写出点E坐标________；点F的坐标___________;‎ ‎（3）在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．‎ 基本图形四：直线上确定一点M，使│AM－BM│最大 图1‎ 图2‎ ‎　‎ 练7．（2013•茂名）如图，抛物线与x轴交于点A和点B，与y轴交于点C，已知点B的坐标为（3，0）．‎ ‎（1）求a的值和抛物线的顶点坐标；‎ ‎（3）设N是抛物线对称轴上的一个动点，d=|AN﹣CN|．探究：是否存在一点N，使d的值最大？若存在，请直接写出点N的坐标和d的最大值；若不存在，请简单说明理由．‎ 补充、其它非基本图形类线段和差最值问题 ‎1、求线段的最大值与最小值需要将该条线段转化到一个三角形中，在该三角形中，其他两边是已知的，则所求线段的最大值为其他两线段之和，最小值为其他两线段之差。‎ ‎2、在转化较难进行时需要借助于三角形的中位线及直角三角形斜边上的中线。‎ ‎3、线段之和的问题往往是将各条线段串联起来，再连接首尾端点，根据两点之间线段最短以及点到线的距离垂线段最短的基本依据解决。‎ 如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.⑴ 求证：△AMB≌△ENB；‎ E A D B C N M ‎⑵ ①当M点在何处时，AM＋CM的值最小；‎ ‎②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；‎ ‎、‎