中考数学综合提高题训练 73页

中考数学综合提高训练 第一部分 函数图象中点的存在性问题 1.1 因动点产生的相似三角形问题 例 1 如图 1，已知抛物线 21 1 ( 1)4 4 4 by x b x    （b 是实数且 b＞2）与 x 轴的正 半轴分别交于点 A、B（点 A 位于点 B 是左侧），与 y 轴的正半轴交于点 C． （1）点 B 的坐标为______，点 C 的坐标为__________（用含 b 的代数式表示）； （2）请你探索在第一象限内是否存在点 P，使得四边形 PCOB 的面积等于 2b，且△PBC 是以点 P 为直角顶点的等腰直角三角形？如果存在，求出点 P 的坐标；如果不存在，请说 明理由； （3）请你进一步探索在第一象限内是否存在点 Q，使得△QCO、△QOA 和△QAB 中的 任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点 Q 的坐标；如 果不存在，请说明理由． 图 1 满分解答 （1）B 的坐标为(b, 0)，点 C 的坐标为(0, 4 b )． （2）如图 2，过点 P 作 PD⊥x 轴，PE⊥y 轴，垂足分别为 D、E，那么△PDB≌△PEC． 因此 PD＝PE．设点 P 的坐标为(x, x)． 如图 3，联结 OP． 所以 S 四边形 PCOB＝S△PCO＋S△PBO＝ 1 1 5 2 4 2 8 b x b x bx      ＝2b． 解得 16 5x  ．所以点 P 的坐标为(16 16,5 5 )． 图 2 图 3 （3）由 21 1 1( 1) ( 1)( )4 4 4 4 by x b x x x b       ，得 A(1, 0)，OA＝1． ①如图 4，以 OA、OC 为邻边构造矩形 OAQC，那么△OQC≌△QOA． 当 BA QA QA OA  ，即 2QA BA OA  时，△BQA∽△QOA． 所以 2( ) 14 b b  ．解得 8 4 3b   ．所以符合题意的点 Q 为(1,2 3 )． 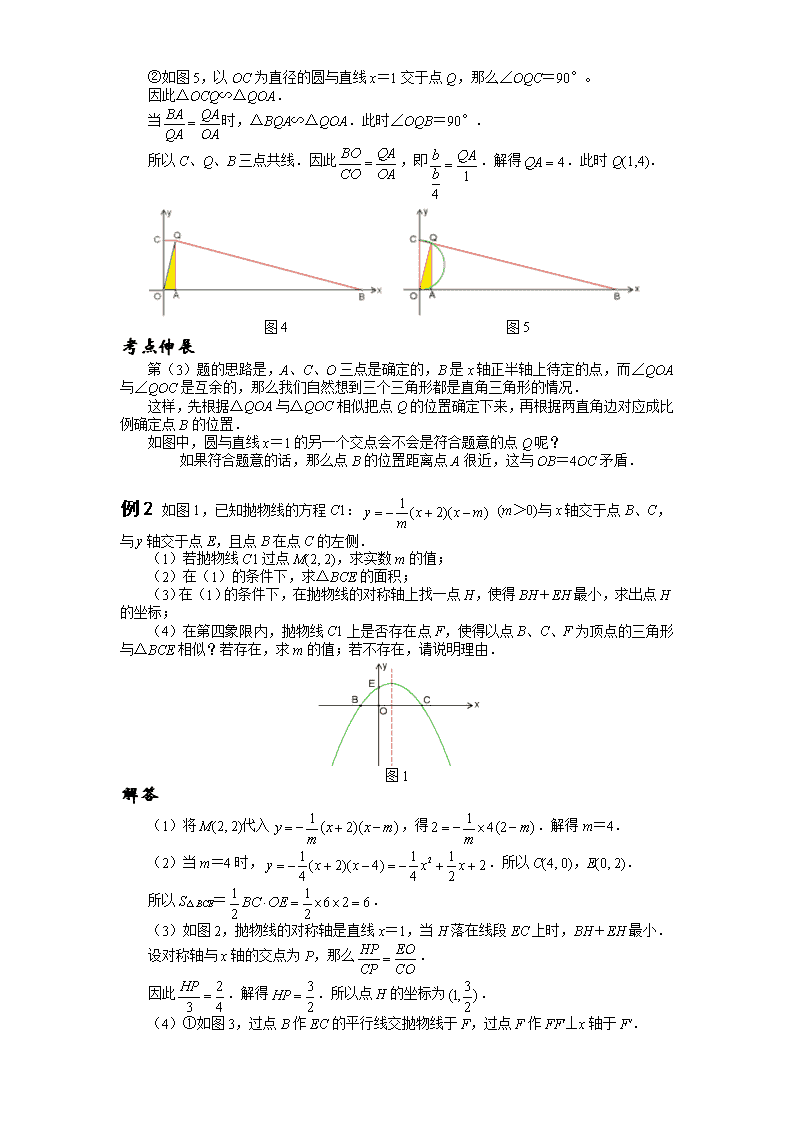②如图 5，以 OC 为直径的圆与直线 x＝1 交于点 Q，那么∠OQC＝90°。 因此△OCQ∽△QOA． 当 BA QA QA OA  时，△BQA∽△QOA．此时∠OQB＝90°． 所以 C、Q、B 三点共线．因此 BO QA CO OA  ，即 1 4 b QA b  ．解得 4QA  ．此时 Q(1,4)． 图 4 图 5 考点伸展 第（3）题的思路是，A、C、O 三点是确定的，B 是 x 轴正半轴上待定的点，而∠QOA 与∠QOC 是互余的，那么我们自然想到三个三角形都是直角三角形的情况． 这样，先根据△QOA 与△QOC 相似把点 Q 的位置确定下来，再根据两直角边对应成比 例确定点 B 的位置． 如图中，圆与直线 x＝1 的另一个交点会不会是符合题意的点 Q 呢？ 如果符合题意的话，那么点 B 的位置距离点 A 很近，这与 OB＝4OC 矛盾． 例 2 如图 1，已知抛物线的方程 C1： 1 ( 2)( )y x x mm     (m＞0)与 x 轴交于点 B、C， 与 y 轴交于点 E，且点 B 在点 C 的左侧． （1）若抛物线 C1 过点 M(2, 2)，求实数 m 的值； （2）在（1）的条件下，求△BCE 的面积； （3）在（1）的条件下，在抛物线的对称轴上找一点 H，使得 BH＋EH 最小，求出点 H 的坐标； （4）在第四象限内，抛物线 C1 上是否存在点 F，使得以点 B、C、F 为顶点的三角形 与△BCE 相似？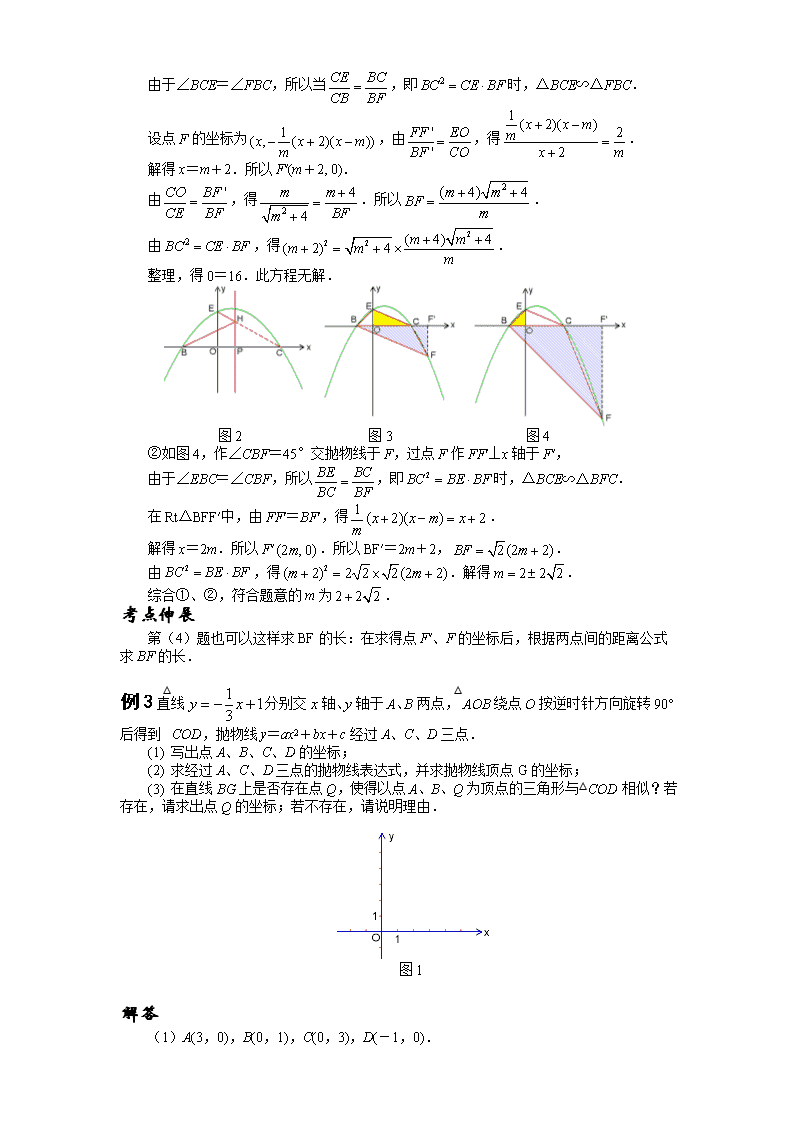若存在，求 m 的值；若不存在，请说明理由． 图 1 解答 （1）将 M(2, 2)代入 1 ( 2)( )y x x mm     ，得 12 4(2 )mm     ．解得 m＝4． （2）当 m＝4 时， 21 1 1( 2)( 4) 24 4 2y x x x x        ．所以 C(4, 0)，E(0, 2)． 所以 S△BCE＝ 1 1 6 2 62 2BC OE     ． （3）如图 2，抛物线的对称轴是直线 x＝1，当 H 落在线段 EC 上时，BH＋EH 最小． 设对称轴与 x 轴的交点为 P，那么 HP EO CP CO  ． 因此 2 3 4 HP  ．解得 3 2HP  ．所以点 H 的坐标为 3(1, )2 ． （4）①如图 3，过点 B 作 EC 的平行线交抛物线于 F，过点 F 作 FF′⊥x 轴于 F′． 由于∠BCE＝∠FBC，所以当 CE BC CB BF  ，即 2BC CE BF  时，△BCE∽△FBC． 设点 F 的坐标为 1( , ( 2)( ))x x x mm    ，由 ' ' FF EO BF CO  ，得 1 ( 2)( ) 2 2 x x mm x m    ． 解得 x＝m＋2．所以 F′(m＋2, 0)． 由 'CO BF CE BF  ，得 2 4 4 m m BFm   ．所以 2( 4) 4m mBF m   ． 由 2BC CE BF  ，得 2 2 2 ( 4) 4( 2) 4 m mm m m      ． 整理，得 0＝16．此方程无解． 图 2 图 3 图 4 ②如图 4，作∠CBF＝45°交抛物线于 F，过点 F 作 FF′⊥x 轴于 F′， 由于∠EBC＝∠CBF，所以 BE BC BC BF  ，即 2BC BE BF  时，△BCE∽△BFC． 在 Rt△BFF′中，由 FF′＝BF′，得 1 ( 2)( ) 2x x m xm     ． 解得 x＝2m．所以 F′(2 ,0)m ．所以 BF′＝2m＋2， 2(2 2)BF m  ． 由 2BC BE BF  ，得 2( 2) 2 2 2(2 2)m m    ．解得 2 2 2m   ． 综合①、②，符合题意的 m 为 2 2 2 ． 考点伸展 第（4）题也可以这样求 BF 的长：在求得点 F′、F 的坐标后，根据两点间的距离公式 求 BF 的长． 例 3 直线 1 13y x   分别交 x 轴、y 轴于 A、B 两点，△AOB 绕点 O 按逆时针方向旋转 90°后得到△COD，抛物线 y＝ax2＋bx＋c 经过 A、C、D 三点． (1) 写出点 A、B、C、D 的坐标； (2) 求经过 A、C、D 三点的抛物线表达式，并求抛物线顶点 G 的坐标； (3) 在直线 BG 上是否存在点 Q，使得以点 A、B、Q 为顶点的三角形与△COD 相似？ 若存在，请求出点 Q 的坐标；若不存在，请说明理由． 图 1 解答 （1）A(3，0)，B(0，1)，C(0，3)，D(－1，0)． （2）因为抛物线 y＝ax2＋bx＋c 经过 A(3，0)、C(0，3)、D(－1，0) 三点，所以 9 3 0, 3, 0. a b c c a b c          解得 1, 2, 3. a b c       所以抛物线的解析式为 y＝－x2＋2x＋3＝－(x－1)2＋4，顶点 G 的坐标为(1，4)． （3）如图 2，直线 BG 的解析式为 y＝3x＋1，直线 CD 的解析式为 y＝3x＋3，因此 CD//BG． 因为图形在旋转过程中，对应线段的夹角等于旋转角，所以 AB⊥CD．因此 AB⊥BG， 即∠ABQ＝90°． 因为点 Q 在直线 BG 上，设点 Q 的坐标为(x，3x＋1)，那么 2 2(3 ) 10BQ x x x    ． Rt△COD 的两条直角边的比为 1∶3，如果 Rt△ABQ 与 Rt△COD 相似，存在两种情况： ①当 3BQ BA  时， 10 3 10 x  ．解得 3x   ．所以 1(3,10)Q ， 2 ( 3, 8)Q   ． ②当 1 3 BQ BA  时， 10 1 310 x  ．解得 1 3x   ．所以 3 1( ,2)3Q ， 4 1( ,0)3Q  ． 图 2 图 3 考点伸展 第（3）题在解答过程中运用了两个高难度动作：一是用旋转的性质说明 AB⊥BG；二 是 2 2(3 ) 10BQ x x x    ． 我们换个思路解答第（3）题： 如图 3，作 GH⊥y 轴，QN⊥y 轴，垂足分别为 H、N． 通过证明△AOB≌△BHG，根据全等三角形的对应角相等，可以证明∠ABG＝90°． 在 Rt△BGH 中， 1sin 1 10   ， 3cos 1 10   ． ①当 3BQ BA  时， 3 10BQ  ． 在 Rt△BQN 中， sin 1 3QN BQ    ， cos 1 9BN BQ    ． 当 Q 在 B 上方时， 1(3,10)Q ；当 Q 在 B 下方时， 2 ( 3, 8)Q   ． ②当 1 3 BQ BA  时， 1 103BQ  ．同理得到 3 1( ,2)3Q ， 4 1( ,0)3Q  ． 例 4 Rt△ABC 在直角坐标系内的位置如图 1 所示，反比例函数 ( 0)ky kx   在第一象限 内的图象与 BC 边交于点 D（4，m），与 AB 边交于点 E（2，n），△BDE 的面积为 2． （1）求 m 与 n 的数量关系； （2）当 tan∠A＝ 1 2 时，求反比例函数的解析式和直线 AB 的表达式； （3）设直线 AB 与 y 轴交于点 F，点 P 在射线 FD 上，在（2）的条件下，如果△AEO 与△EFP 相似，求点 P 的坐标． 图 1 解答 （1）如图 1，因为点 D（4，m）、E（2，n）在反比例函数 ky x  的图象上，所以 4 , 2 . m k n k    整理，得 n＝2m． （2）如图 2，过点 E 作 EH⊥BC，垂足为 H．在 Rt△BEH 中，tan∠BEH＝tan∠A＝ 1 2 ， EH＝2，所以 BH＝1．因此 D(4，m)，E(2，2m)，B(4，2m＋1)． 已知△BDE 的面积为 2，所以 1 1 ( 1) 2 22 2BD EH m     ．解得 m＝1．因此 D(4， 1)，E(2，2)，B(4，3)． 因为点 D（4，1）在反比例函数 ky x  的图象上，所以 k＝4．因此反比例函数的解析 式为 4y x  ． 设直线 AB 的解析式为 y＝kx＋b，代入 B(4，3)、E(2，2)，得 3 4 , 2 2 . k b k b      解得 1 2k  ， 1b  ． 因此直线 AB 的函数解析式为 1 12y x  ． 图 2 图 3 图 4 （3）如图 3，因为直线 1 12y x  与 y 轴交于点 F（0，1），点 D 的坐标为（4，1）， 所以 FD// x 轴，∠EFP＝∠EAO．因此△AEO 与△EFP 相似存在两种情况： ①如图 3，当 EA EF AO FP  时， 2 5 5 2 FP  ．解得 FP＝1．此时点 P 的坐标为（1，1）． ②如图 4，当 EA FP AO EF  时， 2 5 2 5 FP ．解得 FP＝5．此时点 P 的坐标为（5，1）． 考点伸展 本题的题设部分有条件“Rt△ABC 在直角坐标系内的位置如图 1 所示”，如果没有这个 条件限制，保持其他条件不变，那么还有如图 5 的情况： 第（1）题的结论 m 与 n 的数量关系不变．第（2）题反比例函数的解析式为 12y x   ， 直线 AB 为 1 72y x  ．第（3）题 FD 不再与 x 轴平行，△AEO 与△EFP 也不可能相似． 图 5 例 5 如图 1，已知梯形 OABC，抛物线分别过点 O（0，0）、A（2，0）、B（6，3）． （1）直接写出抛物线的对称轴、解析式及顶点 M 的坐标； （2）将图 1 中梯形 OABC 的上下底边所在的直线 OA、CB 以相同的速度同时向上平移， 分别交抛物线于点 O1、A1、C1、B1，得到如图 2 的梯形 O1A1B1C1．设梯形 O1A1B1C1 的面积 为 S，A1、 B1 的坐标分别为 (x1，y1)、(x2，y2)．用含 S 的代数式表示 x2－x1，并求出当 S=36 时点 A1 的坐标； （3）在图 1 中，设点 D 的坐标为(1，3)，动点 P 从点 B 出发，以每秒 1 个单位长度的 速度沿着线段 BC 运动，动点 Q 从点 D 出发，以与点 P 相同的速度沿着线段 DM 运动．P、 Q 两点同时出发，当点 Q 到达点 M 时，P、Q 两点同时停止运动．设 P、Q 两点的运动时间 为 t，是否存在某一时刻 t，使得直线 PQ、直线 AB、x 轴围成的三角形与直线 PQ、直线 AB、 抛物线的对称轴围成的三角形相似？若存在，请求出 t 的值；若不存在，请说明理由． 图 1 图 2 解答 （1）抛物线的对称轴为直线 1x  ，解析式为 21 1 8 4y x x  ，顶点为 M（1， 1 8  ）． （ 2 ） 梯 形 O1A1B1C1 的 面 积 1 2 1 2 2( 1 1) 3( ) 62 x xS x x       ， 由 此 得 到 1 2 23 sx x   ．由于 2 1 3y y  ，所以 2 2 2 1 2 2 1 1 1 1 1 1 38 4 8 4y y x x x x      ．整理，得 2 1 2 1 1 1( ) ( ) 38 4x x x x       ．因此得到 2 1 72x x S   ． 当 S=36 时， 2 1 2 1 14, 2. x x x x      解得 1 2 6, 8. x x    此时点 A1 的坐标为（6，3）． （3）设直线 AB 与 PQ 交于点 G，直线 AB 与抛物线的对称轴交于点 E，直线 PQ 与 x 轴交于点 F，那么要探求相似的△GAF 与△GQE，有一个公共角∠G． 在△GEQ 中，∠GEQ 是直线 AB 与抛物线对称轴的夹角，为定值． 在△GAF 中，∠GAF 是直线 AB 与 x 轴的夹角，也为定值，而且∠GEQ≠∠GAF． 因此只存在∠GQE＝∠GAF 的可能，△GQE∽△GAF．这时∠GAF＝∠GQE＝∠PQD． 由于 3tan 4GAF  ， tan 5 DQ tPQD QP t     ，所以 3 4 5 t t   ．解得 20 7t  ． 图 3 图 4 考点伸展 第（3）题是否存在点 G 在 x 轴上方的情况？如图 4，假如存在，说理过程相同，求得 的 t 的值也是相同的．事实上，图 3 和图 4 都是假设存在的示意图，实际的图形更接近图 3． 例 6 如图 1，已知点 A (-2，4) 和点 B (1，0)都在抛物线 2 2y mx mx n   上． （1）求 m、n； （2）向右平移上述抛物线，记平移后点 A 的对应点为 A′，点 B 的对应点为 B′，若四边 形 A A′B′B 为菱形，求平移后抛物线的表达式； （3）记平移后抛物线的对称轴与直线 AB′ 的交点为 C，试在 x 轴上找一个点 D，使得 以点 B′、C、D 为顶点的三角形与△ABC 相似． 图 1 动感体验 请打开几何画板文件名“10 宝山 24”，拖动点 A′向右平移，可以体验到，平移 5 个单位 后，四边形 A A′B′B 为菱形．再拖动点 D 在 x 轴上运动，可以体验到，△B′CD 与△ABC 相 似有两种情况． 思路点拨 1．点 A 与点 B 的坐标在 3 个题目中处处用到，各具特色．第（1）题用在待定系数法 中；第（2）题用来计算平移的距离；第（3）题用来求点 B′ 的坐标、AC 和 B′C 的长． 2．抛物线左右平移，变化的是对称轴，开口和形状都不变． 3．探求△ABC 与△B′CD 相似，根据菱形的性质，∠BAC＝∠CB′D，因此按照夹角的 两边对应成比例，分两种情况讨论． 满分解答 (1) 因 为 点 A (-2 ， 4) 和 点 B (1 ， 0) 都 在 抛 物 线 2 2y mx mx n   上 ， 所 以 4 4 4, 2 0. m m n m m n        解得 4 3m   ， 4n  ． (2)如图 2，由点 A (-2，4) 和点 B (1，0)，可得 AB＝5．因为四边形 A A′B′B 为菱形，所 以 A A′＝B′B＝ AB＝5．因为 43 8 3 4 2  xxy  24 1613 3x    ，所以原抛物线的对 称轴 x＝－1 向右平移 5 个单位后，对应的直线为 x＝4． 因此平移后的抛物线的解析式为   3 1643 4 2,  xy ． 图 2 (3) 由点 A (-2，4) 和点 B′ (6，0)，可得 A B′＝ 4 5 ． 如图 2，由 AM//CN，可得 ' ' ' ' B N B C B M B A  ，即 2 ' 8 4 5 B C ．解得 ' 5B C  ．所以 3 5AC  ．根据菱形的性质，在△ABC 与△B′CD 中，∠BAC＝∠CB′D． ①如图 3，当 ' ' AB B C AC B D  时， 5 5 '3 5 B D  ，解得 ' 3B D  ．此时 OD＝3，点 D 的坐 标为（3，0）． ②如图 4，当 ' ' AB B D AC B C  时， 5 ' 3 5 5 B D ，解得 5' 3B D  ．此时 OD＝13 3 ，点 D 的 坐标为（13 3 ，0）． 图 3 图 4 考点伸展 在本题情境下，我们还可以探求△B′CD 与△AB B′相似，其实这是有公共底角的两个等 腰三角形，容易想象，存在两种情况． 我们也可以讨论△B′CD 与△CB B′相似，这两个三角形有一组公共角∠B，根据对应边 成比例，分两种情况计算． 例 7 2009 年临沂市中考第 26 题 如图 1，抛物线经过点 A(4，0)、B（1，0)、C（0，－2）三点． （1）求此抛物线的解析式； （2）P 是抛物线上的一个动点，过 P 作 PM⊥x 轴，垂足为 M，是否存在点 P，使得以 A、P、M 为顶点的三角形与△OAC 相似？若存在，请求出符合条件的 点 P 的坐标；若不 存在，请说明理由； （3）在直线 AC 上方的抛物线是有一点 D，使得△DCA 的面积最大，求出点 D 的坐标． , 图 1 动感体验 请打开几何画板文件名“09 临沂 26”，拖动点 P 在抛物线上运动，可以体验到，△PAM 的形状在变化，分别双击按钮“P 在 B 左侧”、“ P 在 x 轴上方”和“P 在 A 右侧”，可以显 示△PAM 与△OAC 相似的三个情景． 双击按钮“第(3)题”， 拖动点 D 在 x 轴上方的抛物线上运动，观察△DCA 的形状和面 积随 D 变化的图象，可以体验到，E 是 AC 的中点时，△DCA 的面积最大． 思路点拨 1．已知抛物线与 x 轴的两个交点，用待定系数法求解析式时，设交点式比较简便． 2．数形结合，用解析式表示图象上点的坐标，用点的坐标表示线段的长． 3．按照两条直角边对应成比例，分两种情况列方程． 4．把△DCA 可以分割为共底的两个三角形，高的和等于 OA． 满分解答 （1 ）因为抛物线与 x 轴交于 A(4，0)、B（1，0)两点，设抛物线的解析式为 )4)(1(  xxay ，代入点 C 的 坐标（0，－2），解得 2 1a ．所以抛物线的解析式为 22 5 2 1)4)(1(2 1 2  xxxxy ． （2）设点 P 的坐标为 ))4)(1(2 1,(  xxx ． ①如图 2，当点 P 在 x 轴上方时，1＜x＜4， )4)(1(2 1  xxPM ， xAM  4 ． 如果 2 CO AO PM AM ，那么 24 )4)(1(2 1   x xx ．解得 5x 不合题意． 如果 2 1 CO AO PM AM ，那么 2 1 4 )4)(1(2 1   x xx ．解得 2x ． 此时点 P 的坐标为（2，1）． ②如图 3，当点 P 在点 A 的右侧时，x＞4， )4)(1(2 1  xxPM ， 4 xAM ． 解方程 24 )4)(1(2 1   x xx ，得 5x ．此时点 P 的坐标为 )2,5(  ． 解方程 2 1 4 )4)(1(2 1   x xx ，得 2x 不合题意． ③如图 4，当点 P 在点 B 的左侧时，x＜1， )4)(1(2 1  xxPM ， xAM  4 ． 解方程 24 )4)(1(2 1   x xx ，得 3x ．此时点 P 的坐标为 )14,3(  ． 解方程 2 1 4 )4)(1(2 1   x xx ，得 0x ．此时点 P 与点 O 重合，不合题意． 综上所述，符合条件的 点 P 的坐标为（2，1）或 )14,3(  或 )2,5(  ． 图 2 图 3 图 4 （3）如图 5，过点 D 作 x 轴的垂线交 AC 于 E．直线 AC 的解析式为 22 1  xy ． 设点 D 的横坐标为 m )41(  m ，那么点 D 的坐标为 )22 5 2 1,( 2  mmm ，点 E 的 坐标为 )22 1,( mm ．所以 )22 1()22 5 2 1( 2  mmmDE mm 22 1 2  ． 因此 4)22 1(2 1 2  mmS DAC mm 42  4)2( 2  m ． 当 2m 时，△DCA 的面积最大，此时点 D 的坐标为（2，1）． 图 5 图 6 考点伸展 第（3）题也可以这样解： 如图 6，过 D 点构造矩形 OAMN，那么△DCA 的面积等于直角梯形 CAMN 的面积减去 △CDN 和△ADM 的面积． 设点 D 的横坐标为（m，n） )41(  m ，那么 42)4(2 1)2(2 14)22(2 1  nmmnnmnS ． 由于 22 5 2 1 2  mmn ，所以 mmS 42  ． 例 8 如图 1，△ABC 中，AB＝5，AC＝3，cosA＝ 3 10 ．D 为射线 BA 上的点（点 D 不与点 B 重合），作 DE//BC 交射线 CA 于点 E.． (1) 若 CE＝x，BD＝y，求 y 与 x 的函数关系式，并写出函数的定义域； (2) 当分别以线段 BD，CE 为直径的两圆相切时，求 DE 的长度； (3) 当点 D 在 AB 边上时，BC 边上是否存在点 F，使△ABC 与△DEF 相似？若存在， 请求出线段 BF 的长；若不存在，请说明理由． 图 1 备用图 备用图 解答 （1）如图 2，作 BH⊥AC，垂足为点 H．在 Rt△ABH 中，AB＝5，cosA＝ 3 10 AH AB  ， 所以 AH＝ 3 2 ＝ 1 2 AC．所以 BH 垂直平分 AC，△ABC 为等腰三角形，AB＝CB＝5． 因为 DE//BC，所以 AB AC DB EC  ，即 5 3 y x  ．于是得到 5 3y x ，（ 0x  ）． （2）如图 3，图 4，因为 DE//BC，所以 DE AE BC AC  ， MN AN BC AC  ，即 | 3 | 5 3 DE x ， 1| 3 |2 5 3 xMN   ．因此 5| 3 | 3 xDE  ，圆心距 5| 6 | 6 xMN  ． 图 2 图 3 图 4 在⊙M 中， 1 1 5 2 2 6Mr BD y x   ，在⊙N 中， 1 1 2 2Nr CE x  ． ①当两圆外切时， 5 1 6 2x x 5| 6 | 6 x ．解得 30 13x  或者 10x   ． 如图 5，符合题意的解为 30 13x  ，此时 5(3 ) 15 3 13 xDE   ． ②当两圆内切时， 5 1 6 2x x 5| 6 | 6 x ． 当 x＜6 时，解得 30 7x  ，如图 6，此时 E 在 CA 的延长线上， 5( 3) 15 3 7 xDE   ； 当 x＞6 时，解得 10x  ，如图 7，此时 E 在 CA 的延长线上， 5( 3) 35 3 3 xDE   ． 图 5 图 6 图 7 （3）因为△ABC 是等腰三角形，因此当△ABC 与△DEF 相似时，△DEF 也是等腰三 角形． 如图 8，当 D、E、F 为△ABC 的三边的中点时，DE 为等腰三角形 DEF 的腰，符合题 意，此时 BF＝2.5．根据对称性，当 F 在 BC 边上的高的垂足时，也符合题意，此时 BF＝4.1． 如图 9，当 DE 为等腰三角形 DEF 的底边时，四边形 DECF 是平行四边形，此时 125 34BF  ． 图 8 图 9 图 10 图 11 考点伸展 第（3）题的情景是一道典型题，如图 10，如图 11，AH 是△ABC 的高，D、E、F 为△ ABC 的三边的中点，那么四边形 DEHF 是等腰梯形． 例 9 图 1 解答 （1） 1OH  ， 3 3k  ， 2 3 3b  ． （2）由抛物线的解析式 ( 1)( 5)y a x x   ，得 点 M 的坐标为 ( 1,0) ，点 N 的坐标为 (5,0) ． 因此 MN 的中点 D 的坐标为（2，0），DN＝3． 因为△AOB 是等腰直角三角形，如果△DNE 与△AOB 相似，那么△DNE 也是等腰直角 三角形． ①如图 2，如果 DN 为直角边，那么点 E 的坐标为 E1（2，3）或 E2（2，－3）． 将 E1（2，3）代入 ( 1)( 5)y a x x   ，求得 1 3a   ． 此时抛物线的解析式为 21 1 4 5( 1)( 5)3 3 3 3y x x x x        ． 将 E2（2，－3）代入 ( 1)( 5)y a x x   ，求得 3 1a ． 此时抛物线的解析式为 3 5 3 4 3 1)5)(1(3 1 2  xxxxy ． ②如果 DN 为斜边，那么点 E 的坐标为 E3 1 1(3 ,1 )2 2 或 E4 )2 11,2 13(  ． 将 E3 1 1(3 ,1 )2 2 代入 ( 1)( 5)y a x x   ，求得 2 9a   ． 此时抛物线的解析式为 22 2 8 10( 1)( 5)9 9 9 9y x x x x        ． 将 E4 )2 11,2 13(  代入 ( 1)( 5)y a x x   ，求得 9 2a ． 此时抛物线的解析式为 9 10 9 8 9 2)5)(1(9 2 2  xxxxy ． 图 2 图 3 对于点 E 为 E1（2，3）和 E3 1 1(3 ,1 )2 2 ，直线 NE 是相同的，∠ENP＝45°． 又∠OBP＝45°，∠P＝∠P，所以△POB∽△PGN． 因此 2101472  PNPOPGPB ． 对于点 E 为 E2（2，－3）和 E4 )2 11,2 13(  ，直线 NE 是相同的． 此时点 G 在直线 5x 的右侧， 33 14PG ． 又 33 4PB ，所以 2103 41433 433 14  PGPB ． 考点伸展 在本题情景下，怎样计算 PB 的长？ 如图 3，作 AF⊥AB 交 OP 于 F，那么△OBC≌△OAF，OF＝OC＝ 2 33 ，PF＝ 22 33  ， PA＝ 3 3 2(2 3) 3 12 2 3PF     ，所以 3 1PB   ． 1.2 因动点产生的等腰三角形问题 例 1 如图 1，抛物线 y＝ax2＋bx＋c 经过 A(－1,0)、B(3, 0)、C(0 ,3)三点，直线 l 是抛物线 的对称轴． （1）求抛物线的函数关系式； （2）设点 P 是直线 l 上的一个动点，当△PAC 的周长最小时，求点 P 的坐标； （3）在直线 l 上是否存在点 M，使△MAC 为等腰三角形，若存在，直接写出所有符合 条件的点 M 的坐标；若不存在，请说明理由． 图 1 解答 （1）因为抛物线与 x 轴交于 A(－1,0)、B(3, 0)两点，设 y＝a(x＋1)(x－3)， 代入点 C(0 ,3)，得－3a＝3．解得 a＝－1． 所以抛物线的函数关系式是 y＝－(x＋1)(x－3)＝－x2＋2x＋3． （2）如图 2，抛物线的对称轴是直线 x＝1． 当点 P 落在线段 BC 上时，PA＋PC 最小，△PAC 的周长最小． 设抛物线的对称轴与 x 轴的交点为 H． 由 BH PH BO CO  ，BO＝CO，得 PH＝BH＝2． 所以点 P 的坐标为(1, 2)． 图 2 （3）点 M 的坐标为(1, 1)、(1, 6 )、(1, 6 )或(1,0)． 考点伸展 第（3）题的解题过程是这样的： 设点 M 的坐标为(1,m)． 在△MAC 中，AC2＝10，MC2＝1＋(m－3)2，MA2＝4＋m2． ①如图 3，当 MA＝MC 时，MA2＝MC2．解方程 4＋m2＝1＋(m－3)2，得 m＝1． 此时点 M 的坐标为(1, 1)． ②如图 4，当 AM＝AC 时，AM2＝AC2．解方程 4＋m2＝10，得 6m   ． 此时点 M 的坐标为(1, 6 )或(1, 6 )． ③如图 5，当 CM＝CA 时，CM2＝CA2．解方程 1＋(m－3)2＝10，得 m＝0 或 6． 当 M(1, 6)时，M、A、C 三点共线，所以此时符合条件的点 M 的坐标为(1,0)． 图 3 图 4 图 5 例 2 如图 1，点 A 在 x 轴上，OA＝4，将线段 OA 绕点 O 顺时针旋转 120°至 OB 的位置． （1）求点 B 的坐标； （2）求经过 A、O、B 的抛物线的解析式； （3）在此抛物线的对称轴上，是否存在点 P，使得以点 P、O、B 为顶点的三角形是等 腰三角形？若存在，求点 P 的坐标；若不存在，请说明理由． 图 1 解答 （1）如图 2，过点 B 作 BC⊥y 轴，垂足为 C． 在 Rt△OBC 中，∠BOC＝30°，OB＝4，所以 BC＝2， 2 3OC  ． 所以点 B 的坐标为 ( 2, 2 3)  ． （2）因为抛物线与 x 轴交于 O、A(4, 0)，设抛物线的解析式为 y＝ax(x－4)， 代入点 B( 2, 2 3)  ， 2 3 2 ( 6)a     ．解得 3 6a   ． 所以抛物线的解析式为 23 3 2 3( 4)6 6 3y x x x x      ． （3）抛物线的对称轴是直线 x＝2，设点 P 的坐标为(2, y)． ①当 OP＝OB＝4 时，OP2＝16．所以 4+y2＝16．解得 2 3y   ． 当 P 在(2,2 3) 时，B、O、P 三点共线（如图 2）． ②当 BP＝BO＝4 时，BP2＝16．所以 2 24 ( 2 3) 16y   ．解得 1 2 2 3y y   ． ③当 PB＝PO 时，PB2＝PO2．所以 2 2 2 24 ( 2 3) 2y y    ．解得 2 3y   ． 综合①、②、③，点 P 的坐标为 (2, 2 3) ，如图 2 所示． 图 2 图 3 考点伸展 如图 3，在本题中，设抛物线的顶点为 D，那么△DOA 与△OAB 是两个相似的等腰三 角形． 由 23 3 2 3( 4) ( 2)6 6 3y x x x       ，得抛物线的顶点为 2 3(2, )3D ． 因此 2 3tan 3DOA  ．所以∠DOA＝30°，∠ODA＝120°． 例 3 如图 1，已知正方形 OABC 的边长为 2，顶点 A、C 分别在 x、y 轴的正半轴上，M 是 BC 的中点．P(0,m)是线段 OC 上一动点（C 点除外），直线 PM 交 AB 的延长线于点 D． （1）求点 D 的坐标（用含 m 的代数式表示）； （2）当△APD 是等腰三角形时，求 m 的值； （3）设过 P、M、B 三点的抛物线与 x 轴正半轴交于点 E，过点 O 作直线 ME 的垂线， 垂足为 H（如图 2）．当点 P 从 O 向 C 运动时，点 H 也随之运动．请直接写出点 H 所经过 的路长（不必写解答过程）． 图 1 图 2 解答 （1）因为 PC//DB，所以 1CP PM MC BD DM MB    ．因此 PM＝DM，CP＝BD＝2－m．所以 AD＝4－m．于是得到点 D 的坐标为(2，4－m)． （2）在△APD 中， 2 2(4 )AD m  ， 2 2 4AP m  ， 2 2 2(2 ) 4 4(2 )PD PM m    ． ①当 AP＝AD 时， 2(4 )m 2 4m  ．解得 3 2m  （如图 3）． ②当 PA＝PD 时， 2 4m  24 4(2 )m   ．解得 4 3m  （如图 4）或 4m  （不合题意， 舍去）． ③当 DA＝DP 时， 2(4 )m 24 4(2 )m   ．解得 2 3m  （如图 5）或 2m  （不合题意， 舍去）． 综上所述，当△APD 为等腰三角形时，m 的值为 3 2 ， 4 3 或 2 3 ． 图 3 图 4 图 5 （3）点 H 所经过的路径长为 5 4  ． 考点伸展 第（2）题解等腰三角形的问题，其中①、②用几何说理的方法，计算更简单： ① 如 图 3 ， 当 AP ＝ AD 时 ， AM 垂 直 平 分 PD ， 那 么 △ PCM ∽ △ MBA ． 所 以 1 2 PC MB CM BA   ．因此 1 2PC  ， 3 2m  ． ②如图 4，当 PA＝PD 时，P 在 AD 的垂直平分线上．所以 DA＝2PO．因此 4 2m m  ．解 得 4 3m  ． 第（2）题的思路是这样的： 如图 6，在 Rt△OHM 中，斜边 OM 为定值，因此以 OM 为直径的⊙G 经过点 H，也就 是说点 H 在圆弧上运动．运动过的圆心角怎么确定呢？如图 7，P 与 O 重合时，是点 H 运 动的起点，∠COH＝45°，∠CGH＝90°． 图 6 图 7 例 4 如图 1，已知一次函数 y＝－x＋7 与正比例函数 4 3y x 的图象交于点 A，且与 x 轴交 于点 B． （1）求点 A 和点 B 的坐标； （2）过点 A 作 AC⊥y 轴于点 C，过点 B 作直线 l//y 轴．动 点 P 从点 O 出发，以每秒 1 个单位长的速度，沿 O—C—A 的路线向点 A 运动；同时直线 l 从点 B 出发，以相同速度 向左平移，在平移过程中，直线 l 交 x 轴于点 R，交线段 BA 或线段 AO 于点 Q．当点 P 到达点 A 时，点 P 和直线 l 都 停止运动．在运动过程中，设动点 P 运动的时间为 t 秒． ①当 t 为何值时，以 A、P、R 为顶点的三角形的面积 为 8？ ②是否存在以 A、P、Q 为顶点的三角形是等腰三角形？ 若存在，求 t 的值；若不存在，请说明理由． 图 1 解答 （1）解方程组 7, 4 ,3 y x y x     得 3, 4. x y    所以点 A 的坐标是(3，4)． 令 7 0y x    ，得 7x  ．所以点 B 的坐标是(7，0)． （2）①如图 2，当 P 在 OC 上运动时，0≤t＜4．由 8APR ACP PORCORAS S S S   △ △ △梯形 ， 得 1 1 13+7 ) 4 4 (4 ) (7 ) 82 2 2t t t t         （ ．整理，得 2 8 12 0t t   ．解得 t＝2 或 t＝6 （舍去）．如图 3，当 P 在 CA 上运动时，△APR 的最大面积为 6． 因此，当 t＝2 时，以 A、P、R 为顶点的三角形的面积为 8． 图 2 图 3 图 4 ②我们先讨论 P 在 OC 上运动时的情形，0≤t＜4． 如图 1，在△AOB 中，∠B＝45°，∠AOB＞45°，OB＝7， 4 2AB  ，所以 OB＞AB．因 此∠OAB＞∠AOB＞∠B． 如图 4，点 P 由 O 向 C 运动的过程中，OP＝BR＝RQ，所以 PQ//x 轴． 因此∠AQP＝45°保持不变，∠PAQ 越来越大，所以只存在∠APQ＝∠AQP 的情况． 此时点 A 在 PQ 的垂直平分线上，OR＝2CA＝6．所以 BR＝1，t＝1． 我们再来讨论 P 在 CA 上运动时的情形，4≤t＜7． 在△APQ 中， 3cos 5A  为定值， 7AP t  ， 5 5 20 3 3 3AQ OA OQ OA OR t      ． 如图 5，当 AP＝AQ 时，解方程 5 207 3 3t t   ，得 41 8t  ． 如图 6，当 QP＝QA 时，点 Q 在 PA 的垂直平分线上，AP＝2(OR－OP)．解方程 7 2[(7 ) ( 4)]t t t     ，得 5t  ． 如 7 ， 当 PA ＝ PQ 时 ， 那 么 1 2cos AQ A AP   ． 因 此 2 cosAQ AP A   ． 解 方 程 5 20 32(7 )3 3 5t t    ，得 226 43t  ． 综上所述，t＝1 或 41 8 或 5 或 226 43 时，△APQ 是等腰三角形． 图 5 图 6 图 7 例 5 如图 1，在直角坐标平面内有点 A(6, 0)，B(0, 8)，C(－4, 0)，点 M、N 分别为线段 AC 和射线 AB 上的动点，点 M 以 2 个单位长度/秒的速度自 C 向 A 方向作匀速运动，点 N 以 5 个单位长度/秒的速度自 A 向 B 方向作匀速运动，MN 交 OB 于点 P． (1)求证：MN∶NP 为定值； (2)若△BNP 与△MNA 相似，求 CM 的长； (3)若△BNP 是等腰三角形，求 CM 的长． 图 1 解答 (1)如图 2，图 3，作 NQ⊥x 轴，垂足为 Q．设点 M、N 的运动时间为 t 秒． 在 Rt△ANQ 中，AN＝5t，NQ＝4t ，AQ＝3t． 在图 2 中，QO＝6－3t，MQ＝10－5t，所以 MN∶NP＝MQ∶QO＝5∶3． 在图 3 中，QO＝3t－6，MQ＝5t－10，所以 MN∶NP＝MQ∶QO＝5∶3． (2)因为△BNP 与△MNA 有一组邻补角，因此这两个三角形要么是一个锐角三角形和一 个钝角三角形，要么是两个直角三角形．只有当这两个三角形都是直角三角形时才可能相似． 如图 4，△BNP∽△MNA，在 Rt△AMN 中， 3 5 AN AM  ，所以 5 3 10 2 5 t t  ．解得 30 31t  ．此 时 CM 60 31  ． 图 2 图 3 图 4 (3)如图 5，图 6，图 7 中， OP MP QN MN  ，即 2 4 5 OP t  ．所以 8 5OP t ． ①当 N 在 AB 上时，在△BNP 中，∠B 是确定的， 88 5BP t  ， 10 5BN t  ． (Ⅰ)如图 5，当 BP＝BN 时，解方程 88 10 55 t t   ，得 10 17t  ．此时 CM 20 17  ． (Ⅱ)如图 6，当 NB＝NP 时， 4 5BE BN ．解方程  1 8 48 10 52 5 5t t      ，得 5 4t  ．此 时 CM 5 2  ． (Ⅲ)当 PB＝PN 时，1 4 2 5BN BP ．解方程  1 4 810 5 82 5 5t t      ，得 t 的值为负数， 因此不存在 PB＝PN 的情况． ②如图 7，当点 N 在线段 AB 的延长线上时，∠B 是钝角，只存在 BP＝BN 的可能，此 时 5 10BN t  ．解方程 88 5 105 t t   ，得 30 11t  ．此时 CM 60 11  ． 图 5 图 6 图 7 考点伸展 如图 6，当 NB＝NP 时，△NMA 是等腰三角形， 1 4 2 5BN BP ，这样计算简便一些． 例 6 如图 1，在矩形 ABCD 中，AB＝m（m 是大于 0 的常数），BC＝8，E 为线段 BC 上的 动点（不与 B、C 重合）．连结 DE，作 EF⊥DE，EF 与射线 BA 交于点 F，设 CE＝x，BF ＝y． （1）求 y 关于 x 的函数关系式； （2）若 m＝8，求 x 为何值时，y 的值最大，最大值是多少？ （3）若 12y m  ，要使△DEF 为等腰三角形，m 的值应为多少？ 图 1 解答 (1)因为∠EDC 与∠FEB 都是∠DEC 的余角，所以∠EDC＝∠FEB．又因为∠C＝∠B＝ 90°，所以△DCE∽△EBF．因此 DC EB CE BF  ，即 8m x x y  ．整理，得 y 关于 x 的函数关 系为 21 8y x xm m    ． (2)如图 2，当 m＝8 时， 2 21 1 ( 4) 28 8y x x x       ．因此当 x＝4 时，y 取得最大 值为 2． (3) 若 12y m  ，那么 212 1 8x xm m m    ．整理，得 2 8 12 0x x   ．解得 x＝2 或 x＝6．要 使△DEF 为等腰三角形，只存在 ED＝EF 的情况．因为△DCE∽△EBF，所以 CE＝BF，即 x＝y．将 x＝y ＝2 代入 12y m  ，得 m＝6（如图 3）；将 x＝y ＝6 代入 12y m  ，得 m＝2（如 图 4）． 图 2 图 3 图 4 例 7 已知：如图 1，在平面直角坐标系 xOy 中，矩形 OABC 的边 OA 在 y 轴的正半轴上， OC 在 x 轴的正半轴上，OA＝2，OC＝3，过原点 O 作∠AOC 的平分线交 AB 于点 D，连结 DC，过点 D 作 DE⊥DC，交 OA 于点 E． （1）求过点 E、D、C 的抛物线的解析式； （2）将∠EDC 绕点 D 按顺时针方向旋转后，角的一边与 y 轴的正半轴交于点 F，另一 边与线段 OC 交于点 G．如果 DF 与（1）中的抛物线交于另一点 M，点 M 的横坐标为 5 6 ， 那么 EF＝2GO 是否成立？若成立，请给予证明；若不成立，请说明理由； （3）对于（2）中的点 G，在位于第一象限内的该抛物线上是否存在点 Q，使得直线 GQ 与 AB 的交点 P 与点 C、G 构成的△PCG 是等腰三角形？若存在，请求出点 Q 的坐标； 若不存在成立，请说明理由． 图 1 解答 （1）由于 OD 平分∠AOC，所以点 D 的坐标为（2，2），因此 BC＝AD＝1． 由于△BCD≌△ADE，所以 BD＝AE＝1，因此点 E 的坐标为（0，1）． 设过 E、D、C 三点的抛物线的解析式为 cbxaxy  2 ，那么       .039 ,224 ,1 cba cba c 解 得 6 5a ， 6 13b 1c ．因此过 E、D、C 三点的抛物线的解析式为 16 13 6 5 2  xxy ． （2）把 5 6x 代入 16 13 6 5 2  xxy ，求得 5 12y ．所 以点 M 的坐标为      5 12,5 6 ． 如图 2，过点 M 作 MN⊥AB，垂足为 N，那么 DA DN FA MN  ， 即 2 5 6225 12    FA ．解得 1FA ． 因为∠EDC 绕点 D 旋转的过程中，△DCG≌△DEF，所 以 CG＝EF＝2．因此 GO＝1，EF＝2GO． （3）在第（2）中，GC＝2．设点 Q 的坐标为       16 13 6 5, 2 xxx ． ①如图 3，当 CP＝CG＝2 时，点 P 与点 B（3，2）重合，△PCG 是等腰直角三角形．此 时 GQQ xxy  ，因此 116 13 6 5 2  xxx 。由此得到点 Q 的坐标为      5 7,5 12 ． ②如图 4，当 GP＝GC＝2 时，点 P 的坐标为（1，2）．此时点 Q 的横坐标为 1，点 Q 图 2 的坐标为      6 13,1 ． ③如图 5，当 PG＝PC 时，点 P 在 GC 的垂直平分线上，点 P、Q 与点 D 重合．此时点 Q 的坐标为（2，2）． 图 3 图 4 图 5 考点伸展 在第（2）题情景下，∠EDC 绕点 D 旋转的过程中，FG 的长怎样变化？ 设 AF 的长为 m，那么 82)2()2( 222  mmmFG ． 点 F 由 E 开始沿射线 EA 运动的过程中，FG 先是越来越小，F 与 A 重合时，FG 达到 最小值 22 ；F 经过点 A 以后，FG 越来越大，当 C 与 O 重合时，FG 达到最大值 4． 例 8 如图 1，在等腰梯形 ABCD 中，AD//BC，E 是 AB 的中点，过点 E 作 EF//BC 交 CD 于点 F，AB＝4，BC＝6，∠B＝60°． （1）求点 E 到 BC 的距离； （2）点 P 为线段 EF 上的一个动点，过点 P 作 PM⊥EF 交 BC 于 M，过 M 作 MN//AB 交折线 ADC 于 N，连结 PN，设 EP＝x． ①当点 N 在线段 AD 上时（如图 2），△PMN 的形状是否发生改变？若不变，求出△PMN 的周长；若改变，请说明理由； ②当点 N 在线段 DC 上时（如图 3），是否存在点 P，使△PMN 为等腰三角形？若存在， 请求出所有满足条件的 x 的值；若不存在，请说明理由． 图 1 图 2 图 3 解答 （1）如图 4，过点 E 作 EG⊥BC 于 G． 在 Rt△BEG 中， 22 1  ABBE ，∠B＝60°， 所以 160cos  BEBG ， 360sin  BEEG ． 所以点 E 到 BC 的距离为 3 ． （2）因为 AD//EF//BC，E 是 AB 的中点，所以 F 是 DC 的中点． 因此 EF 是梯形 ABCD 的中位线，EF＝4． ①如图 4，当点 N 在线段 AD 上时，△PMN 的形状不是否发生改变． 过点 N 作 NH⊥EF 于 H，设 PH 与 NM 交于点 Q． 在矩形 EGMP 中，EP＝GM＝x，PM＝EG＝ 3 ． 在平行四边形 BMQE 中，BM＝EQ＝1＋x． 所以 BG＝PQ＝1． 因为 PM 与 NH 平行且相等，所以 PH 与 NM 互相平分，PH＝2PQ＝2． 在 Rt△PNH 中，NH＝ 3 ，PH＝2，所以 PN＝ 7 ． 在平行四边形 ABMN 中，MN＝AB＝4． 因此△PMN 的周长为 3 ＋ 7 ＋4． 图 4 图 5 ②当点 N 在线段 DC 上时，△CMN 恒为等边三角形． 如图 5，当 PM＝PN 时，△PMC 与△PNC 关于直线 PC 对称，点 P 在∠DCB 的平分线 上． 在 Rt△PCM 中，PM＝ 3 ，∠PCM＝30°，所以 MC＝3． 此时 M、P 分别为 BC、EF 的中点，x＝2． 如图 6，当 MP＝MN 时，MP＝MN＝MC＝ 3 ，x＝GM＝GC－MC＝5－ 3 ． 如图 7，当 NP＝NM 时，∠NMP＝∠NPM＝30°，所以∠PNM＝120°． 又因为∠FNM＝120°，所以 P 与 F 重合． 此时 x＝4． 综上所述，当 x＝2 或 4 或 5－ 3 时，△PMN 为等腰三角形． 图 6 图 7 图 8 1.3 因动点产生的直角三角形问题 例 1 如图 1，抛物线 23 3 38 4y x x    与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C． （1）求点 A、B 的坐标； （2）设 D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积 时，求点 D 的坐标； （3）若直线 l 过点 E(4, 0)，M 为直线 l 上的动点，当以 A、B、M 为顶点所作的直角三 角形有且只有．．．．三个时，求直线 l 的解析式． 图 1 解答 （1）由 23 3 33 ( 4)( 2)8 4 8y x x x x        ， 得抛物线与 x 轴的交点坐标为 A(－4, 0)、B(2, 0)．对称轴是直线 x＝－1． （2）△ACD 与△ACB 有公共的底边 AC，当△ACD 的面积等于△ACB 的面积时，点 B、 D 到直线 AC 的距离相等． 过点 B 作 AC 的平行线交抛物线的对称轴于点 D，在 AC 的另一侧有对应的点 D′． 设抛物线的对称轴与 x 轴的交点为 G，与 AC 交于点 H． 由 BD//AC，得∠DBG＝∠CAO．所以 3 4 DG CO BG AO   ． 所以 3 9 4 4DG BG  ，点 D 的坐标为 9(1, )4  ． 因为 AC//BD，AG＝BG，所以 HG＝DG． 而 D′H＝DH，所以 D′G＝3DG 27 4  ．所以 D′的坐标为 27(1, )4 ． 图 2 图 3 （3）过点 A、B 分别作 x 轴的垂线，这两条垂线与直线 l 总是有交点的，即 2 个点 M． 以 AB 为直径的⊙G 如果与直线 l 相交，那么就有 2 个点 M；如果圆与直线 l 相切，就 只有 1 个点 M 了． 联结 GM，那么 GM⊥l． 在 Rt△EGM 中，GM＝3，GE＝5，所以 EM＝4． 在 Rt△EM1A 中，AE＝8， 1 1 3tan 4 M AM EA AE    ，所以 M1A＝6． 所以点 M1 的坐标为(－4, 6)，过 M1、E 的直线 l 为 3 34y x   ． 根据对称性，直线 l 还可以是 3 34y x  ． 例 2 在平面直角坐标系中，反比例函数与二次函数 y＝k(x2＋x－1)的图象交于点 A(1,k)和点 B(－1,－k)． （1）当 k＝－2 时，求反比例函数的解析式； （2）要使反比例函数与二次函数都是 y 随 x 增大而增大，求 k 应满足的条件以及 x 的 取值范围； （3）设二次函数的图象的顶点为 Q，当△ABQ 是以 AB 为斜边的直角三角形时，求 k 的值． 解答 （1）因为反比例函数的图象过点 A(1,k)，所以反比例函数的解析式是 ky x  ． 当 k＝－2 时，反比例函数的解析式是 2y x   ． （2）在反比例函数 ky x  中，如果 y 随 x 增大而增大， 那么 k＜0． 当 k＜0 时，抛物线的开口向下，在对称轴左侧，y 随 x 增大而增大． 抛物线 y＝k(x2＋x＋1)＝ 21 5( )2 4k x k  的对称轴是直 线 1 2x   ． 图 1 所以当 k＜0 且 1 2x   时，反比例函数与二次函数都是 y 随 x 增大而增大． （3）抛物线的顶点 Q 的坐标是 1 5( , )2 4 k  ，A、B 关于原点 O 中心对称， 当 OQ＝OA＝OB 时，△ABQ 是以 AB 为直径的直角三角形． 由 OQ2＝OA2，得 2 2 2 21 5( ) ( ) 12 4 k k     ． 解得 1 2 33k  （如图 2）， 2 2 33k   （如图 3）． 图 2 图 3 考点伸展 如图 4，已知经过原点 O 的两条直线 AB 与 CD 分别与双曲线 ky x  （k＞0）交于 A、B 和 C、D，那么 AB 与 CD 互相平分，所以四边形 ACBD 是平行四边形． 问平行四边形 ABCD 能否成为矩形？能否成为正方形？ 如图 5，当 A、C 关于直线 y＝x 对称时，AB 与 CD 互相平分且相等，四边形 ABCD 是 矩形． 因为 A、C 可以无限接近坐标系但是不能落在坐标轴上，所以 OA 与 OC 无法垂直，因 此四边形 ABCD 不能成为正方形． 图 4 图 5 例 3 如图 1，已知抛物线 y＝x2＋bx＋c 与 x 轴交于 A、B 两点（点 A 在点 B 左侧），与 y 轴交于点 C(0，－3)，对称轴是直线 x＝1，直线 BC 与抛物线的对称轴交于点 D． （1）求抛物线的函数表达式； （2）求直线 BC 的函数表达式； （3）点 E 为 y 轴上一动点，CE 的垂直平分线交 CE 于点 F，交抛物线于 P、Q 两点， 且点 P 在第三象限． ①当线段 3 4PQ AB 时，求 tan∠CED 的值； ②当以 C、D、E 为顶点的三角形是直角三角形时，请直接写出点 P 的坐标． 温馨提示：考生可以根据第（3）问的题意，在图中补出图形，以便作答． 图 1 解答 （1）设抛物线的函数表达式为 2( 1)y x n   ，代入点 C(0，－3)，得 4n   ．所以抛 物线的函数表达式为 2 2( 1) 4 2 3y x x x      ． （2）由 2 2 3 ( 1)( 3)y x x x x      ，知 A(－1，0)，B(3，0)．设直线 BC 的函数表达 式为 y kx b  ，代入点 B(3，0)和点 C(0，－3)，得 3 0, 3. k b b      解得 1k  ， 3b   ．所以 直线 BC 的函数表达式为 3y x  ． （3）①因为 AB＝4，所以 3 34PQ AB  ．因为 P、Q 关于直线 x＝1 对称，所以点 P 的横坐标为 1 2  ．于是得到点 P 的坐标为 1 7,2 4      ，点 F 的坐标为 70, 4     ．所以 7 53 4 4FC OC OF     ， 52 2EC FC  ． 进而得到 5 13 2 2OE OC EC     ，点 E 的坐标为 10, 2     ． 直线 BC: 3y x  与抛物线的对称轴 x＝1 的交点 D 的坐标为（1，－2）． 过点 D 作 DH⊥y 轴，垂足为 H． 在 Rt△EDH 中，DH＝1， 1 32 2 2EH OH OE     ，所以 tan∠CED 2 3 DH EH   ． ② 1(1 2, 2)P   ， 2 6 5(1 , )2 2P   ． 图 2 图 3 图 4 考点伸展 第（3）题②求点 P 的坐标的步骤是： 如图 3，图 4，先分两种情况求出等腰直角三角形 CDE 的顶点 E 的坐标，再求出 CE 的 中点 F 的坐标，把点 F 的纵坐标代入抛物线的解析式，解得的 x 的较小的一个值就是点 P 的横坐标． 例 4 设直线 l1：y＝k1x＋b1 与 l2：y＝k2x＋b2，若 l1⊥l2，垂足为 H，则称直线 l1 与 l2 是点 H 的直角线． （1）已知直线① 1 22y x   ；② 2y x  ；③ 2 2y x  ；④ 2 4y x  和点 C(0，2)，则直线_______和_______是点 C 的直角线 （填序号即可）； （2）如图，在平面直角坐标系中，直角梯形 OABC 的顶点 A(3， 0)、B(2，7)、C(0，7)，P 为线段 OC 上一点，设过 B、P 两点的直 线为 l1，过 A、P 两点的直线为 l2，若 l1 与 l2 是点 P 的直角线，求 直线 l1 与 l2 的解析式． 图 1 答案 （1）直线①和③是点 C 的直角线． （2）当∠APB＝90°时，△BCP∽△POA．那么 BC PO CP OA  ，即 2 7 3 PO PO  ．解得 OP ＝6 或 OP＝1． 如图 2，当 OP＝6 时，l1： 1 62y x  ， l2：y＝－2x＋6． 如图 3，当 OP＝1 时，l1：y＝3x＋1， l2： 1 13y x   ． 图 2 图 3 例 5 在平面直角坐标系 xOy 中，抛物线 2 21 5 3 24 4 m my x x m m      与 x 轴的交 点分别为原点 O 和点 A，点 B(2,n)在这条抛物线上． （1）求点 B 的坐标； （2）点 P 在线段 OA 上，从点 O 出发向点 A 运动，过点 P 作 x 轴的垂线，与直线 OB 交于点 E，延长 PE 到点 D，使得 ED＝PE，以 PD 为斜边，在 PD 右侧作等腰直角三角形 PCD（当点 P 运动时，点 C、D 也随之运动）． ①当等腰直角三角形 PCD 的顶点 C 落在此抛物线上时，求 OP 的长； ②若点 P 从点 O 出发向点 A 作匀速运动，速度为每秒 1 个单位，同时线段 OA 上另一 个点 Q 从点 A 出发向点 O 作匀速运动，速度为每秒 2 个单位（当点 Q 到达点 O 时停止运动， 点 P 也停止运动）．过 Q 作 x 轴的垂线，与直线 AB 交于点 F，延长 QF 到点 M，使得 FM＝ QF，以 QM 为斜边，在 QM 的左侧作等腰直角三角形 QMN（当点 Q 运动时，点 M、N 也 随之运动）．若点 P 运动到 t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线 上，求此刻 t 的值． 图 1 解答 (1) 因 为 抛 物 线 2 21 5 3 24 4 m my x x m m      经 过 原 点 ， 所 以 2 3 2 0m m   ． 解得 1 2m  ， 2 1m  （舍去）．因此 21 5 4 2y x x   ．所以点 B 的坐 标为（2，4）． (2) ①如图 4，设 OP 的长为 t，那么 PE＝2t，EC＝2t，点 C 的坐标为(3t, 2t)．当点 C 落在抛物线上时， 21 52 (3 ) 34 2t t t     ．解得 22 9t OP  ． ②如图 1，当两条斜边 PD 与 QM 在同一条直线上时，点 P、Q 重合．此时 3t＝10．解 得 10 3t  ． 如图 2，当两条直角边 PC 与 MN 在同一条直线上，△PQN 是等腰直角三角形，PQ＝ PE．此时10 3 2t t  ．解得 2t  ． 如图 3，当两条直角边 DC 与 QN 在同一条直线上，△PQC 是等腰直角三角形，PQ＝ PD．此时10 3 4t t  ．解得 10 7t  ． 图 1 图 2 图 3 考点伸展 在本题情境下，如果以 PD 为直径的圆 E 与以 QM 为直径的圆 F 相切，求 t 的值． 如图 5，当 P、Q 重合时，两圆内切， 10 3t  ． 如图 6，当两圆外切时， 30 20 2t   ． 图 4 图 5 图 6 例 6 如图 1，已知 A、B 是线段 MN 上的两点， 4MN ， 1MA ， 1MB ．以 A 为中心 顺时针旋转点 M，以 B 为中心逆时针旋转点 N，使 M、N 两点重合成一点 C，构成△ABC， 设 xAB  ． （1）求 x 的取值范围； （2）若△ABC 为直角三角形，求 x 的值； （3）探究：△ABC 的最大面积？ 图 1 解答 （1）在 △ ABC 中， 1AC ， xAB  ， xBC  3 ，所以      .31 ,31 xx xx 解得 21  x ． （2）①若 AC 为斜边，则 22 )3(1 xx  ，即 0432  xx ，此方程无实根． ②若 AB 为斜边，则 1)3( 22  xx ，解得 3 5x ，满足 21  x ． ③若 BC 为斜边，则 22 1)3( xx  ，解得 3 4x ，满足 21  x ． 因此当 3 5x 或 3 4x 时，△ABC 是直角三角形． （3）在 △ ABC 中，作 ABCD  于 D，设 hCD  ， △ ABC 的面积为 S，则 xhS 2 1 ． ① 如 图 2 ， 若 点 D 在 线 段 AB 上 ， 则 xhxh  222 )3(1 ． 移 项 ， 得 222 1)3( hxhx  ．两边平方，得 22222 112)3( hhxxhx  ．整理， 得 431 2  xhx ． 两 边 平 方 ， 得 16249)1( 222  xxhx ． 整 理 ， 得 16248 222  xxhx 所以 4624 1 2222  xxhxS 2 1)2 3(2 2  x （ 4 23 x ≤ ）． 当 2 3x 时（满足 4 23 x ≤ ）， 2S 取最大值 2 1 ，从而 S 取最大值 2 2 ． 图 2 图 3 ②如图 3，若点 D 在线段 MA 上，则 xhhx  222 1)3( ． 同理可得， 4624 1 2222  xxhxS 2 1)2 3(2 2  x （ 41 3x ≤ ）． 易知此时 2 2S ． 综合①②得， △ ABC 的最大面积为 2 2 ． 考点伸展 第（3）题解无理方程比较烦琐，迂回一下可以避免烦琐的运算：设 aAD  ， 例如在图 2 中，由 2222 BDBCADAC  列方程 222 )()3(1 axxa  ． 整理，得 x xa 43  ．所以 21 a 2 22 16248431 x xx x x       ． 因此 462)1(4 1 2222  xxaxS ． 例 7 如图 1，直线 43 4  xy 和 x 轴、y 轴的交点分别为 B、C，点 A 的坐标是（-2，0）． （1）试说明△ABC 是等腰三角形； （2）动点 M 从 A 出发沿 x 轴向点 B 运动，同时动点 N 从点 B 出发沿线段 BC 向点 C 运动，运动的速度均为每秒 1 个单位长度．当其中一个动点到达终点时，他们都停止运动．设 M 运动 t 秒时，△MON 的面积为 S． ① 求 S 与 t 的函数关系式； ② 设点 M 在线段 OB 上运动时，是否存在 S＝4 的情形？若存在，求出对应的 t 值；若 不存在请说明理由； ③在运动过程中，当△MON 为直角三角形时，求 t 的值． 图 1 解答 （1）直线 43 4  xy 与 x 轴的交点为 B（3，0）、与 y 轴的交点 C（0，4）．Rt△BOC 中，OB＝3，OC＝4，所以 BC＝5．点 A 的坐标是（-2，0），所以 BA＝5．因此 BC＝BA， 所以△ABC 是等腰三角形． （2）①如图 2，图 3，过点 N 作 NH⊥AB，垂足为 H．在 Rt△BNH 中，BN＝t， 4sin 5B  ， 所以 4 5NH t ． 如图 2，当 M 在 AO 上时，OM＝2－t，此时 21 1 4 2 4(2 )2 2 5 5 5S OM NH t t t t         ． 定义域为 0＜t≤2． 如图 3，当 M 在 OB 上时，OM＝t－2，此时 21 1 4 2 4( 2)2 2 5 5 5S OM NH t t t t        ． 定义域为 2＜t≤5． 图 2 图 3 ②把 S＝4 代入 22 4 5 5S t t  ，得 22 4 45 5t t  ．解得 1 2 11t   ， 2 2 11t   （舍 去负值）．因此，当点 M 在线段 OB 上运动时，存在 S＝4 的情形，此时 2 11t   ． ③如图 4，当∠OMN＝90°时，在 Rt△BNM 中，BN＝t，BM 5 t  ， 3cos 5B  ，所 以 5 3 5 t t   ．解得 25 8t  ． 如图 5，当∠OMN＝90°时，N 与 C 重合， 5t  ．不存在∠ONM＝90°的可能． 所以，当 25 8t  或者 5t  时，△MON 为直角三角形． 图 4 图 5 考点伸展 在本题情景下，如果△MON 的边与 AC 平行，求 t 的值． 如图 6，当 ON//AC 时，t＝3；如图 7，当 MN//AC 时，t＝2.5． 图 6 图 7 例 8 如图 1，直线 43 4  xy 和 x 轴、y 轴的交点分别为 B、C，点 A 的坐标是（-2，0）． （1）试说明△ABC 是等腰三角形； （2）动点 M 从 A 出发沿 x 轴向点 B 运动，同时动点 N 从点 B 出发沿线段 BC 向点 C 运动，运动的速度均为每秒 1 个单位长度．当其中一个动点到达终点时，他们都停止运动．设 M 运动 t 秒时，△MON 的面积为 S． ① 求 S 与 t 的函数关系式； ② 设点 M 在线段 OB 上运动时，是否存在 S＝4 的情形？若存在，求出对应的 t 值；若 不存在请说明理由； ③在运动过程中，当△MON 为直角三角形时，求 t 的值． 图 1 解答 （1）直线 43 4  xy 与 x 轴的交点为 B（3，0）、与 y 轴的交点 C（0，4）． Rt△BOC 中，OB＝3，OC＝4，所以 BC＝5． 点 A 的坐标是（-2，0），所以 BA＝5． 因此 BC＝BA，所以△ABC 是等腰三角形． （2）①如图 2，图 3，过点 N 作 NH⊥AB，垂足为 H． 在 Rt△BNH 中，BN＝t， 4sin 5B  ，所以 4 5NH t ． 如图 2，当 M 在 AO 上时，OM＝2－t，此时 21 1 4 2 4(2 )2 2 5 5 5S OM NH t t t t         ．定义域为 0＜t≤2． 如图 3，当 M 在 OB 上时，OM＝t－2，此时 21 1 4 2 4( 2)2 2 5 5 5S OM NH t t t t        ．定义域为 2＜t≤5． 图 2 图 3 ②把 S＝4 代入 22 4 5 5S t t  ，得 22 4 45 5t t  ． 解得 1 2 11t   ， 2 2 11t   （舍去负值）． 因此，当点 M 在线段 OB 上运动时，存在 S＝4 的情形，此时 2 11t   ． ③如图 4，当∠OMN＝90°时，在 Rt△BNM 中，BN＝t，BM 5 t  ， 3cos 5B  ， 所以 5 3 5 t t   ．解得 25 8t  ． 如图 5，当∠OMN＝90°时，N 与 C 重合， 5t  ． 不存在∠ONM＝90°的可能． 所以，当 25 8t  或者 5t  时，△MON 为直角三角形． 图 4 图 5 考点伸展 在本题情景下，如果△MON 的边与 AC 平行，求 t 的值． 如图 6，当 ON//AC 时，t＝3；如图 7，当 MN//AC 时，t＝2.5． 图 6 图 7 1.4 因动点产生的平行四边形问题 例 1 如图 1，在 Rt△ABC 中，∠C＝90°，AC＝6，BC＝8，动点 P 从点 A 开始沿 边 AC 向点 C 以每秒 1 个单位长度的速度运动，动点 Q 从点 C 开始沿边 CB 向点 B 以每秒 2 个单位长度的速度运动，过点 P 作 PD//BC，交 AB 于点 D，联结 PQ．点 P、Q 分别从点 A、 C 同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为 t 秒（t≥0）． （1）直接用含 t 的代数式分别表示：QB＝_______，PD＝_______； （2）是否存在 t 的值，使四边形 PDBQ 为菱形？若存在，求出 t 的值；若不存在，说 明理由，并探究如何改变点 Q 的速度（匀速运动），使四边形 PDBQ 在某一时刻为菱形，求 点 Q 的速度； （3）如图 2，在整个运动过程中，求出线段 PQ 的中点 M 所经过的路径长． 图 1 图 2 解答 （1）QB＝8－2t，PD＝ 4 3 t ． （2）如图 3，作∠ABC 的平分线交 CA 于 P，过点 P 作 PQ//AB 交 BC 于 Q，那么四边 形 PDBQ 是菱形． 过点 P 作 PE⊥AB，垂足为 E，那么 BE＝BC＝8． 在 Rt △ ABC 中 ， AC ＝ 6 ， BC ＝ 8 ， 所 以 AB ＝ 10． 图 3 在 Rt△APE 中， 2 3cos 5 AEA AP t    ，所以 10 3t  ． 当 PQ//AB 时， CQ CP CB CA  ，即 106 3 8 6 CQ   ．解得 32 9CQ  ． 所以点 Q 的运动速度为 32 10 16 9 3 15   ． （3）以 C 为原点建立直角坐标系． 如图 4，当 t＝0 时，PQ 的中点就是 AC 的中点 E(3，0)． 如图 5，当 t＝4 时，PQ 的中点就是 PB 的中点 F(1，4)． 直线 EF 的解析式是 y＝－2x＋6． 如图 6，PQ 的中点 M 的坐标可以表示为（ 6 2 t ，t）．经验证，点 M（ 6 2 t ，t）在直 线 EF 上． 所以 PQ 的中点 M 的运动路径长就是线段 EF 的长，EF＝ 2 5 ． 图 4 图 5 图 6 考点伸展 第（3）题求点 M 的运动路径还有一种通用的方法是设二次函数： 当 t＝2 时，PQ 的中点为(2，2)． 设点 M 的运动路径的解析式为 y＝ax2＋bx＋c，代入 E(3，0)、F(1，4)和(2，2)， 得 9 3 0, 4, 4 2 2. a b c a b c a b c            解得 a＝0，b＝－2，c＝6． 所以点 M 的运动路径的解析式为 y＝－2x＋6． 例 2 如图 1，在平面直角坐标系中，已知矩形 ABCD 的三个顶点 B(1, 0)、C(3, 0)、 D(3, 4)．以 A 为顶点的抛物线 y＝ax2＋bx＋c 过点 C．动点 P 从点 A 出发，沿线段 AB 向点 B 运动，同时动点 Q 从点 C 出发，沿线段 CD 向点 D 运动．点 P、Q 的运动速度均为每秒 1 个单位，运动时间为 t 秒．过点 P 作 PE⊥AB 交 AC 于点 E． （1）直接写出点 A 的坐标，并求出抛物线的解析式； （2）过点 E 作 EF⊥AD 于 F，交抛物线于点 G，当 t 为何值时，△ACG 的面积最大？ 最大值为多少？ （3）在动点 P、Q 运动的过程中，当 t 为何值时，在矩形 ABCD 内（包括边界）存在 点 H，使以 C、Q、E、H 为顶点的四边形为菱形？请直接写出 t 的值． 图 1 解答 （1）A(1, 4)．因为抛物线的顶点为 A，设抛物线的解析式为 y＝a(x－1)2＋4， 代入点 C(3, 0)，可得 a＝－1． 所以抛物线的解析式为 y＝－(x－1)2＋4＝－x2＋2x＋3． （2）因为 PE//BC，所以 2AP AB PE BC   ．因此 1 1 2 2PE AP t  ． 所以点 E 的横坐标为 11 2 t ． 将 11 2x t  代入抛物线的解析式，y＝－(x－1)2＋4＝ 214 4 t ． 所以点 G 的纵坐标为 214 4 t ．于是得到 2 21 1(4 ) (4 )4 4GE t t t t       ． 因此 2 21 1 1( ) ( 2) 12 4 4ACG AGE CGES S S GE AF DF t t t             ． 所以当 t＝1 时，△ACG 面积的最大值为 1． （3） 20 13t  或 20 8 5t   ． 考点伸展 第（3）题的解题思路是这样的： 因为 FE//QC，FE＝QC，所以四边形 FECQ 是平行四边形．再构造点 F 关于 PE 轴对称 的点 H′，那么四边形 EH′CQ 也是平行四边形． 再根据 FQ＝CQ 列关于 t 的方程，检验四边形 FECQ 是否为菱形，根据 EQ＝CQ 列关 于 t 的方程，检验四边形 EH′CQ 是否为菱形． 1(1 ,4 )2E t t  ， 1(1 ,4)2F t ， (3, )Q t ， (3,0)C ． 如图 2，当 FQ＝CQ 时，FQ2＝CQ2，因此 2 2 21( 2) (4 )2 t t t    ． 整理，得 2 40 80 0t t   ．解得 1 20 8 5t   ， 2 20 8 5t   （舍去）． 如图 3，当 EQ＝CQ 时，EQ2＝CQ2，因此 2 2 21( 2) (4 2 )2 t t t    ． 整理，得 213 72 800 0t t   ． (13 20)( 40) 0t t   ．所以 1 20 13t  ， 2 40t  （舍去）． 图 2 图 3 例 3 已知平面直角坐标系 xOy（如图 1），一次函数 3 34y x  的图象与 y 轴交于 点 A，点 M 在正比例函数 3 2y x 的图象上，且 MO＝MA．二 次函数 y＝x2＋bx＋c 的图象经过点 A、M． （1）求线段 AM 的长； （2）求这个二次函数的解析式； （3）如果点 B 在 y 轴上，且位于点 A 下方，点 C 在上述 二次函数的图象上，点 D 在一次函数 3 34y x  的图象上，且 四边形 ABCD 是菱形，求点 C 的坐标． 图 1 解答 （1）当 x＝0 时， 3 3 34y x   ，所以点 A 的坐标为(0，3)，OA＝3． 如图 2，因为 MO＝MA，所以点 M 在 OA 的垂直平分线上，点 M 的纵坐标为 3 2 ．将 3 2y  代入 3 2y x ，得 x＝1．所以点 M 的坐标为 3(1, )2 ．因此 13 2AM  ． （2）因为抛物线 y＝x2＋bx＋c 经过 A(0，3)、M 3(1, )2 ，所以 3, 31 .2 c b c     解得 5 2b   ， 3c  ．所以二次函数的解析式为 2 5 32y x x   ． （3）如图 3，设四边形 ABCD 为菱形，过点 A 作 AE⊥CD，垂足为 E． 在 Rt△ADE 中，设 AE＝4m，DE＝3m，那么 AD＝5m． 因此点 C 的坐标可以表示为(4m，3－2m)．将点 C(4m，3－2m)代入 2 5 32y x x   ，得 23 2 16 10 3m m m    ．解得 1 2m  或者 m＝0（舍去）． 因此点 C 的坐标为（2，2）． 图 2 图 3 考点伸展 如果第（3）题中，把“四边形 ABCD 是菱形”改为“以 A、B、C、D 为顶点的四边形 是菱形”，那么还存在另一种情况： 如图 4，点 C 的坐标为 7 27( , )4 16 ． 图 4 例 4 将抛物线 c1： 23 3y x   沿 x 轴翻折，得到抛物线 c2，如图 1 所示． （1）请直接写出抛物线 c2 的表达式； （2）现将抛物线 c1 向左平移 m 个单位长度，平移后得到新抛物线的顶点为 M，与 x 轴 的交点从左到右依次为 A、B；将抛物线 c2 向右也平移 m 个单位长度，平移后得到新抛物线 的顶点为 N，与 x 轴的交点从左到右依次为 D、E． ①当 B、D 是线段 AE 的三等分点时，求 m 的值； ②在平移过程中，是否存在以点 A、N、E、M 为顶点的四边形是矩形的情形？若存在， 请求出此时 m 的值；若不存在，请说明理由． 图 1 解答 （1）抛物线 c2 的表达式为 23 3y x  ． （2）抛物线 c1： 23 3y x   与 x 轴的两个交点为(－1，0)、(1，0)，顶点为(0, 3)． 抛物线 c2： 23 3y x  与 x 轴的两个交点也为(－1，0)、(1，0)，顶点为(0, 3) ． 抛物线 c1 向左平移 m 个单位长度后，顶点 M 的坐标为( , 3)m ，与 x 轴的两个交点为 ( 1 ,0)A m  、 (1 ,0)B m ，AB＝2． 抛物线 c2 向右平移 m 个单位长度后，顶点 N 的坐标为 ( , 3)m  ，与 x 轴的两个交点为 ( 1 ,0)D m  、 (1 ,0)E m ．所以 AE＝(1＋m)－(－1－m)＝2(1＋m)． ①B、D 是线段 AE 的三等分点，存在两种情况： 情形一，如图 2，B 在 D 的左侧，此时 1 23AB AE  ，AE＝6．所以 2(1＋m)＝6．解得 m＝2． 情形二，如图 3，B 在 D 的右侧，此时 2 23AB AE  ，AE＝3．所以 2(1＋m)＝3．解得 1 2m  ． 图 2 图 3 图 4 ②如果以点 A、N、E、M 为顶点的四边形是矩形，那么 AE＝MN＝2OM．而 OM2＝m2 ＋3，所以 4(1＋m)2＝4(m2＋3)．解得 m＝1（如图 4）． 考点伸展 第（2）题②，探求矩形 ANEM，也可以用几何说理的方法： 在等腰三角形 ABM 中，因为 AB＝2，AB 边上的高为 3 ，所以△ABM 是等边三角形． 同理△DEN 是等边三角形．当四边形 ANEM 是矩形时，B、D 两点重合． 因为起始位置时 BD＝2，所以平移的距离 m＝1． 例 5 如图 1，在平面直角坐标系中，已知抛物线经过 A(－4,0)、B(0,－4)、C(2,0) 三点． （1）求抛物线的解析式； （2）若点 M 为第三象限内抛物线上一动点，点 M 的横坐标为 m，△MAB 的面积为 S， 求 S 关于 m 的函数关系式，并求出 S 的最大值； （3）若点 P 是抛物线上的动点，点 Q 是直线 y＝－x 上的动点，判断有几个位置能使 以点 P、Q、B、O 为顶点的四边形为平行四边形，直接写出相应的点 Q 的坐标． 图 1 图 2 解答 (1) 因为抛物线与 x 轴交于 A(－4,0)、C(2,0)两点，设 y＝a(x＋4)(x－2)．代入点 B(0,－ 4)，求得 1 2a  ．所以抛物线的解析式为 21 1( 4)( 2) 42 2y x x x x      ． (2)如图 2，直线 AB 的解析式为 y＝－x－4．过点 M 作 x 轴的垂线交 AB 于 D，那么 2 21 1( 4) ( 4) 22 2MD m m m m m         ．所以 21 42MDA MDBS S S MD OA m m        2( 2) 4m    ． 因此当 2m   时，S 取得最大值，最大值为 4． (3) 如果以点 P、Q、B、O 为顶点的四边形是平行四边形，那么 PQ//OB，PQ＝OB＝4． 设点 Q 的坐标为 ( , )x x ，点 P 的坐标为 21( , 4)2x x x  ． ①当点 P 在点 Q 上方时， 21( 4) ( ) 42 x x x     ．解得 2 2 5x    ． 此时点 Q 的坐标为 ( 2 2 5,2 2 5)   （如图 3），或 ( 2 2 5,2 2 5)   （如图 4）． ②当点 Q 在点 P 上方时， 21( ) ( 4) 42x x x     ． 解得 4x   或 0x  （与点 O 重合，舍去）．此时点 Q 的坐标为(－4,4) （如图 5）． 图 3 图 4 图 5 考点伸展 在本题情境下，以点 P、Q、B、O 为顶点的四边形能成为直角梯形吗？ 如图 6，Q(2,－2)；如图 7，Q(－2,2)；如图 8，Q(4,－4)． 图 6 图 7 图 8 例 6 在直角梯形 OABC 中，CB//OA，∠COA＝90°，CB＝3，OA＝6，BA＝3 5 ．分 别以 OA、OC 边所在直线为 x 轴、y 轴建立如图 1 所示的平面直角坐标系． （1）求点 B 的坐标； （2）已知 D、E 分别为线段 OC、OB 上的点，OD＝5，OE＝2EB，直线 DE 交 x 轴于 点 F．求直线 DE 的解析式； （3）点 M 是（2）中直线 DE 上的一个动点，在 x 轴上方的平面内是否存在另一点 N， 使以 O、D、M、N 为顶点的四边形是菱形？若存在，请求出点 N 的坐标；若不存在，请说 明理由． 图 1 图 2 解答 (1)如图 2，作 BH⊥x 轴，垂足为 H，那么四边形 BCOH 为矩形，OH＝CB＝3． 在 Rt△ABH 中，AH＝3，BA＝3 5 ，所以 BH＝6．因此点 B 的坐标为(3,6)． (2) 因为 OE＝2EB，所以 2 23E Bx x  ， 2 43E By y  ，E(2,4)． 设直线 DE 的解析式为 y＝kx＋b，代入 D(0,5)，E(2,4)，得 5, 2 4. b k b     解得 1 2k   ， 5b  ．所以直线 DE 的解析式为 1 52y x   ． (3) 由 1 52y x   ，知直线 DE 与 x 轴交于点 F(10,0)，OF＝10，DF＝5 5 ． ①如图 3，当 DO 为菱形的对角线时，MN 与 DO 互相垂直平分，点 M 是 DF 的中点．此 时点 M 的坐标为(5, 5 2 )，点 N 的坐标为(－5, 5 2 )． ②如图 4，当 DO、DN 为菱形的邻边时，点 N 与点 O 关于点 E 对称，此时点 N 的坐标 为(4,8)． ③如图 5，当 DO、DM 为菱形的邻边时，NO＝5，延长 MN 交 x 轴于 P． 由△NPO∽△DOF，得 NP PO NO DO OF DF   ，即 5 5 10 5 5 NP PO  ．解得 5NP  ， 2 5PO  ．此时点 N 的坐标为 ( 2 5, 5) ． 图 3 图 4 考点伸展 如果第（3）题没有限定点 N 在 x 轴上方的平面内，那么菱形还有如图 6 的情形． 图 5 图 6 例 7 如图 1，等边△ABC 的边长为 4，E 是边 BC 上的动点，EH⊥AC 于 H，过 E 作 EF∥AC，交线段 AB 于点 F，在线段 AC 上取点 P，使 PE＝EB．设 EC＝x（0＜x≤2）． （1）请直接写出图中与线段 EF 相等的两条线段（不再另外添加辅助线）； （2）Q 是线段 AC 上的动点，当四边形 EFPQ 是平行四边形时，求平行四边形 EFPQ 的面积（用含 x 的代数式表示）； （3）当（2）中 的平行四边形 EFPQ 面积最大值时，以 E 为圆心，r 为半径作圆，根 据⊙E 与此时平行四边形 EFPQ 四条边交点的总个数，求相应的 r 的取值范围． 图 1 解答 （1）BE、PE、BF 三条线段中任选两条． （2）如图 2，在 Rt△CEH 中，∠C＝60°，EC＝x，所以 xEH 2 3 ．因为 PQ＝FE ＝BE＝4－x，所以 xxxxEHPQS EFPQ 322 3)4(2 3 2 平行四边形 ． （3）因为 xxS EFPQ 322 3 2 平行四边形 3222 3 2  ）（x ，所以当 x＝2 时， 平行四边形 EFPQ 的面积最大． 此时 E、F、P 分别为△ABC 的三边 BC、AB、AC 的中点，且 C、Q 重合，四边形 EFPQ 是边长为 2 的菱形（如图 3）． 图 2 图 3 过点 E 点作 ED⊥FP 于 D，则 ED＝EH＝ 3 ． 如图 4，当⊙E 与平行四边形 EFPQ 的四条边交点的总个数是 2 个时，0＜r＜ 3 ； 如图 5，当⊙E 与平行四边形 EFPQ 的四条边交点的总个数是 4 个时，r＝ 3 ； 如图 6，当⊙E 与平行四边形 EFPQ 的四条边交点的总个数是 6 个时， 3 ＜r＜2； 如图 7，当⊙E 与平行四边形 EFPQ 的四条边交点的总个数是 3 个时，r＝2 时； 如图 8，当⊙E 与平行四边形 EFPQ 的四条边交点的总个数是 0 个时，r＞2 时． 图 4 图 5 图 6 图 7 图 8 考点伸展 本题中 E 是边 BC 上的动点，设 EC＝x，如果没有限定 0＜x≤2，那么平行四边形 EFPQ 的面积是如何随 x 的变化而变化的？ 事实上，当 x＞2 时，点 P 就不存在了，平行四边形 EFPQ 也就不存在了． 因此平行四边形 EFPQ 的面积随 x 的增大而增大． 例 8 如图 1，抛物线 322  xxy 与 x 轴相交于 A、B 两点（点 A 在点 B 的左 侧），与 y 轴相交于点 C，顶点为 D． （1）直接写出 A、B、C 三点的坐标和抛物线的对称轴； （2）连结 BC，与抛物线的对称轴交于点 E，点 P 为线段 BC 上的一个动点，过点 P 作 PF//DE 交抛物线于点 F，设点 P 的横坐标为 m． ①用含 m 的代数式表示线段 PF 的长，并求出当 m 为何值时，四边形 PEDF 为平行四 边形？ ②设△BCF 的面积为 S，求 S 与 m 的函数关系． 图 1 解答 （1）A（－1，0），B（3，0），C（0，3）．抛物线的对称轴是 x＝1． （2）①直线 BC 的解析式为 y＝－x＋3． 把 x＝1 代入 y＝－x＋3，得 y＝2．所以点 E 的坐标为（1，2）． 把 x＝1 代入 322  xxy ，得 y＝4．所以点 D 的坐标为（1，4）． 因此 DE=2． 因为 PF//DE，点 P 的横坐标为 m，设点 P 的坐标为 )3,( mm ，点 F 的坐标为 )32,0( 2  mm ，因此 mmmmmFP 3)3()32( 22  ． 当四边形 PEDF 是平行四边形时，DE=FP．于是得到 232  mm ．解得 21 m ， 12 m （与点 E 重合，舍去）． 因此，当 m=2 时，四边形 PEDF 是平行四边形时． ②设直线 PF 与 x 轴交于点 M，那么 OM+BM=OB=3．因此 BMFPOMFPSSSS CPFBPFBCF   2 1 2 1 mmmm 2 9 2 33)3(2 1 22  ． m 的变化范围是 0≤m≤3． 图 2 图 3 考点伸展 在本题条件下，四边形 PEDF 可能是等腰梯形吗？如果可能，求 m 的值；如果不可能， 请说明理由． 如图 4，如果四边形 PEDF 是等腰梯形，那么 DG=EH，因此 EPFD yyyy  ． 于是 2)3()32(4 2  mmm ．解得 01 m （与点 CE 重合，舍去）， 12 m （与点 E 重合，舍去）． 因此四边形 PEDF 不可能成为等腰梯形． 图 4 1.5 因动点产生的梯形问题 例 1 已知直线 y＝3x－3 分别与 x 轴、y 轴交于点 A，B，抛物线 y＝ax2＋2x＋c 经过 点 A，B． （1）求该抛物线的表达式，并写出该抛物线的对称轴和顶 点坐标； （2）记该抛物线的对称轴为直线 l，点 B 关于直线 l 的对称 点为 C，若点 D 在 y 轴的正半轴上，且四边形 ABCD 为梯形． ①求点 D 的坐标； ②将此抛物线向右平移，平移后抛物线的顶点为 P，其对称 轴与直线 y＝3x－3 交于点 E，若 7 3tan DPE ，求四边形 BDEP 的面积． 图 1 解答 （1）直线 y＝3x－3 与 x 轴的交点为 A(1，0)，与 y 轴的交点为 B(0,－3)． 将 A(1，0)、B(0,－3)分别代入 y＝ax2＋2x＋c， 得 2 0, 3. a c c       解得 1, 3. a c     所以抛物线的表达式为 y＝x2＋2x－3． 对称轴为直线 x＝－1，顶点为(－1,－4)． （2）①如图 2，点 B 关于直线 l 的对称点 C 的坐标为(－2,－3)． 因为 CD//AB，设直线 CD 的解析式为 y＝3x＋b， 代入点 C(－2,－3)，可得 b＝3． 所以点 D 的坐标为（0，3）． ②过点 P 作 PH⊥y 轴，垂足为 H，那么∠PDH＝∠DPE． 由 7 3tan DPE ，得 3tan 7 PHPDH DH    ． 而 DH＝7，所以 PH＝3． 因此点 E 的坐标为（3，6）． 所以 1 ( ) 242BDEPS BD EP PH   梯形 ． 图 2 图 3 考点伸展 第（2）①用几何法求点 D 的坐标更简便： 因为 CD//AB，所以∠CDB＝∠ABO． 因此 1 3 BC OA BD OB   ．所以 BD＝3BC＝6，OD＝3．因此 D（0，3）． 例 2 如图 1，把两个全等的 Rt△AOB 和 Rt△COD 方别置于平面直角坐标系中，使直角边 OB、OD 在 x 轴上．已 知点 A(1，2)，过 A、C 两点的直线分别交 x 轴、y 轴于点 E、F．抛物线 y＝ax2＋bx＋c 经过 O、A、C 三点． （1）求该抛物线的函数解析式； （2）点 P 为线段 OC 上的一个动点，过点 P 作 y 轴的平行线交抛物线于点 M，交 x 轴 于点 N，问是否存在这样的点 P，使得四边形 ABPM 为等腰梯形？若存在，求出此时点 P 的坐标；若不存在，请说明理由； （3）若△AOB 沿 AC 方向平移（点 A 始终在线段 AC 上，且不与点 C 重合），△AOB 在平移的过程中与△COD 重叠部分的面积记为 S．试探究 S 是否存在最大值？若存在，求 出这个最大值；若不存在，请说明理由． 图 1 解答 （1）将 A(1，2)、O(0，0)、C(2，1)分别代入 y＝ax2＋bx＋c， 得 2, 0, 4 2 1. a b c c a b c          解得 3 2a   ， 7 2b  ， 0c  ． 所以 23 7 2 2y x x   ． （2）如图 2，过点 P、M 分别作梯形 ABPM 的高 PP′、MM′，如果梯形 ABPM 是等腰 梯形，那么 AM′＝BP′，因此 yA－y M′＝yP′－yB． 直线 OC 的解析式为 1 2y x ，设点 P 的坐标为 1( , )2x x ，那么 23 7( , )2 2M x x x  ． 解方程 23 7 12 ( )2 2 2x x x    ，得 1 2 3x  ， 2 2x  ． x＝2 的几何意义是 P 与 C 重合，此时梯形不存在．所以 2 1( , )3 3P ． 图 2 图 3 （3）如图 3，△AOB 与△COD 重叠部分的形状是四边形 EFGH，作 EK⊥OD 于 K． 设点 A′移动的水平距离为 m，那么 OG＝1＋m，GB′＝m． 在 Rt△OFG 中， 1 1 (1 )2 2FG OG m   ．所以 21 (1 )4OFGS m   ． 在 Rt△A′HG 中，A′G＝2－m，所以 1 1 1' (2 ) 12 2 2HG A G m m     ． 所以 1 3(1 ) (1 )2 2OH OG HG m m m       ． 在 Rt△OEK 中，OK＝2 EK；在 Rt△EHK 中，EK＝2HK；所以 OK＝4HK． 因此 4 4 3 23 3 2OK OH m m    ．所以 1 2EK OK m  ． 所以 21 1 3 3 2 2 2 4OEHS OH EK m m m       ． 于是 2 2 21 3 1 1 1(1 )4 4 2 2 4OFG OEHS S S m m m m          21 1 3( )2 2 8m    ． 因为 0＜m＜1，所以当 1 2m  时，S 取得最大值，最大值为 3 8 ． 考点伸展 第（3）题也可以这样来解：设点 A′的横坐标为 a． 由直线 AC：y＝－x＋3，可得 A′(a, －a＋3)． 由直线 OC： 1 2y x ，可得 1( , )2F a a ． 由直线 OA：y＝2x 及 A′(a, －a＋3)，可得直线 O′A′：y＝2x－3a＋3， 3 3( ,0)2 aH  ． 由直线 OC 和直线 O′A′可求得交点 E(2a－2，a－1)． 由 E、F、G、H 4 个点的坐标，可得 例 3 已知平面直角坐标系 xOy 中， 抛物线 y＝ax2－(a＋1)x 与直线 y＝kx 的一个 公共点为 A(4，8)． （1）求此抛物线和直线的解析式； （2）若点 P 在线段 OA 上，过点 P 作 y 轴的平行线交（1）中抛物线于点 Q，求线段 PQ 长度的最大值； （3）记（1）中抛物线的顶点为 M，点 N 在此抛物线上，若四边形 AOMN 恰好是梯形， 求点 N 的坐标及梯形 AOMN 的面积． 备用图 答案 （1）抛物线的解析式为 y＝x2－2x，直线的解析式为 y＝2x． （2）如图 1，当 P 为 OA 的中点时， PQ 的长度取得最大值为 4． （3）如图 2，如果四边形 AOMN 是梯形，那么点 N 的坐标为(3，3)，梯形 AOMN 的面 积为 9． 图 1 图 2 例 4 已知二次函数的图象经过 A（2，0）、C(0，12) 两点，且对称轴为直线 x＝ 4，设顶点为点 P，与 x 轴的另一交点为点 B． （1）求二次函数的解析式及顶点 P 的坐标； （2）如图 1，在直线 y＝2x 上是否存在点 D，使四边形 OPBD 为等腰梯形？若存在， 求出点 D 的坐标；若不存在，请说明理由； （3）如图 2，点 M 是线段 OP 上的一个动点（O、P 两点除外），以每秒 2 个单位长度 的速度由点 P 向点 O 运动，过点 M 作直线 MN//x 轴，交 PB 于点 N． 将△PMN 沿直线 MN 对折，得到△P1MN． 在动点 M 的运动过程中，设△P1MN 与梯形 OMNB 的重叠部分的面 积为 S，运动时间为 t 秒，求 S 关于 t 的函数关系式． 图 1 图 2 解答 （1）设抛物线的解析式为 2( 4)y a x k   ，代入 A（2，0）、C(0，12) 两点，得 4 0, 16 12. a k a k      解得 1, 4. a k     所以二次函数的解析式为 2 2( 4) 4 8 12y x x x      ，顶点 P 的坐标为（4，－4）． （2）由 2 8 12 ( 2)( 6)y x x x x      ，知点 B 的坐标为（6，0）． 假设在等腰梯形 OPBD，那么 DP＝OB＝6．设点 D 的坐标为(x，2x)． 由两点间的距离公式，得 2 2( 4) (2 4) 36x x    ．解得 2 5x  或 x＝－2． 如图 3，当 x＝－2 时，四边形 ODPB 是平行四边形． 所以，当点 D 的坐标为( 5 2 ， 5 4 )时，四边形 OPBD 为等腰梯形． 图 3 图 4 图 5 （3）设△PMN 与△POB 的高分别为 PH、PG． 在 Rt△PMH 中， 2PM t ， PH MH t  ．所以 ' 2 4P G t  ． 在 Rt△PNH 中， PH t ， 1 1 2 2NH PH t  ．所以 3 2MN t ． ① 如图 4，当 0＜t≤2 时，重叠部分的面积等于△PMN 的面积．此时 21 3 3 2 2 4S t t t    ． ②如图 5，当 2＜t＜4 时，重叠部分是梯形，面积等于△PMN 的面积减去△P′DC 的面 积．由于 2 ' 'P DC PMN S P G S PH      △ △ ，所以 2 2 2 ' 2 4 3 3 (2 4)4 4P DC tS t tt       △ ． 此时 2 2 23 3 9(2 4) 12 124 4 4S t t t t       ． 考点伸展 第（2）题最好的解题策略就是拿起尺、规画图： 方法一，按照对角线相等画圆．以 P 为圆心，OB 长为半径画圆，与直线 y＝2x 有两个 交点，一个是等腰梯形的顶点，一个是平行四边形的顶点． 方法二，按照对边相等画圆．以 B 为圆心，OP 长为半径画圆，与直线 y＝2x 有两个交 点，一个是等腰梯形的顶点，一个是平行四边形的顶点． 例 5 如图 1，在平面直角坐标系 xOy 中，抛物线的解析式是 y ＝ 21 14 x  ，点 C 的坐标为(–4，0)，平行四边形 OABC 的顶点 A，B 在抛物线上，AB 与 y 轴交于点 M，已知 点 Q(x，y)在抛物线上，点 P(t，0)在 x 轴上． (1) 写出点 M 的坐标； (2) 当四边形 CMQP 是以 MQ，PC 为腰的梯形时． ① 求 t 关于 x 的函数解析式和自变量 x 的取值范围； ② 当梯形 CMQP 的两底的长度之比为 1∶2 时，求 t 的值． 图 1 解答 (1)因为 AB＝OC＝ 4，A、B 关于 y 轴对称，所以点 A 的横坐标为 2．将 x＝2 代入 y＝ 21 14 x  ，得 y＝2．所以点 M 的坐标为（0，2）． (2) ① 如图 2，过点 Q 作 QH  x 轴，设垂足为 H，则 HQ＝y 21 14 x  ，HP＝x– t ． 因 为 CM//PQ ， 所 以 ∠ QPH ＝ ∠ MCO ． 因 此 tan ∠ QPH ＝ tan ∠ MCO ， 即 1 2 HQ OM HP OC   ．所以 21 11 ( )4 2x x t   ．整理，得 21 22t x x    ． 如图 3，当 P 与 C 重合时， 4t   ，解方程 214 22 x x     ，得 1 5x   ． 如图 4，当 Q 与 B 或 A 重合时，四边形为平行四边形，此时，x＝ 2． 因此自变量 x 的取值范围是 1 5x   ，且 x 2 的所有实数． 图 2 图 3 图 4 ②因为 sin∠QPH＝sin∠MCO，所以 HQ OM PQ CM  ，即 PQ HQ CM OM  ． 当 1 2 PQ HQ CM OM   时， 1 12HQ OM  ．解方程 21 1 14 x   ，得 0x  （如图 5）．此 时 2t   ． 当 2PQ HQ CM OM   时， 2 4HQ OM  ．解方程 21 1 44 x   ，得 2 3x   ． 如图 6，当 2 3x  时， 8 2 3t    ；如图 6，当 2 3x   时， 8 2 3t    ． 图 5 图 6 图 7 考点伸展 本题情境下，以 Q 为圆心、QM 为半径的动圆与 x 轴有怎样的位置关系呢？ 设点 Q 的坐标为 21, 14x x    ，那么 2 2 2 2 2 21 11 14 4QM x x x              ． 而点 Q 到 x 轴的距离为 21 14 x  ． 因此圆 Q 的半径 QM 等于圆心 Q 到 x 轴的距离，圆 Q 与 x 轴相切． 例 6 已知，矩形 OABC 在平面直角坐标系中位置如图 1 所示，点 A 的坐标为(4,0)， 点 C 的坐标为 )20( ， ，直线 xy 3 2 与边 BC 相交于点 D． (1)求点 D 的坐标； (2)抛物线 cbxaxy  2 经过点 A、D、O，求此抛物线的表达式； (3)在这个抛物线上是否存在点 M，使 O、D、A、M 为顶点的四边形是梯形？若存在， 请求出所有符合条件的点 M 的坐标；若不存在，请说明理由． 图 1 解答 (1)因为 BC//x 轴，点 D 在 BC 上，C(0,－2)，所以点 D 的纵坐标为－2．把 y＝－2 代入 xy 3 2 ，求得 x＝3．所以点 D 的坐标为(3,－2)． (2)由于抛物线与 x 轴交于点 O、A(4,0)，设抛物线的解析式为 y＝ax(x－4)，代入 D (3, －2)，得 2 3a  ．所求的二次函数解析式为 22 2 8( 4)3 3 3y x x x x    ． (3) 设点 M 的坐标为 22 8, 3 3x x x    ． ①如图 2，当 OM//DA 时，作 MN⊥x 轴，DQ⊥x 轴，垂足分别为 N、Q．由 tan∠MON ＝tan∠DAQ，得 22 8 3 3 2 x x x   ． 因为 x＝0 时点 M 与 O 重合，因此 2 8 23 3x   ，解得 x＝7．此时点 M 的坐标为（7， 14）． ②如图 3，当 AM//OD 时，由 tan∠MAN＝tan∠DOQ，得 22 8 23 3 4 3 x x x   ． 因为 x＝4 时点 M 与 A 重合，因此 2 2 3 3x  ，解得 x＝－1．此时点 M 的坐标为 10( 1, )3  ． ③如图 4，当 DM//OA 时，点 M 与点 D 关于抛物线的对称轴对称，此时点 M 的坐标为 （1，－2）． 图 2 图 3 图 4 考点伸展 第（3）题的①、②用几何法进行计算，依据是两直线平行，内错角的正切相等． 如果用代数法进行，计算过程比较麻烦．以①为例，先求出直线 AD 的解析式，再求出 直线 OM 的解析式，最后解由直线 OM 和抛物线的解析式组成的二元二次方程组． 例 7 如图 1，二次函数 )0(2  pqpxxy 的图象与 x 轴交于 A、B 两点，与 y 轴交于点 C（0，－1），△ABC 的面积为 4 5 ． （1）求该二次函数的关系式； （2）过 y 轴上的一点 M（0，m）作 y 轴的垂线，若该垂线与△ABC 的外接圆有公共点， 求 m 的取值范围； （3）在该二次函数的图象上是否存在点 D，使以 A、B、C、D 为顶点的四边形为直角 梯形？若存在，求出点 D 的坐标；若不存在，请说明理由． 图 1 解答 （1）因为 OC＝1，△ABC 的面积为 4 5 ，所以 AB＝ 2 5 ． 设点 A 的坐标为（a，0），那么点 B 的坐标为（a＋ 2 5 ，0）． 设抛物线的解析式为 )2 5)((  axaxy ，代入点 C（0，－1），得 1)2 5( aa ．解 得 2 1a 或 2a ． 因为二次函数的解析式 qpxxy  2 中， 0p ，所以抛物线的对称轴在 y 轴右侧．因 此点 A、B 的坐标分别为 )0,2 1( ， )0,2( ． 所以抛物线的解析式为 12 3)2)(2 1( 2  xxxxy ． （2）如图 2，因为 1OBOA ， 12 OC ，所以 OB OC OC OA  ．因此△AOC∽△COB．所 以△ABC 是以 AB 为斜边的直角三角形，外接圆的直径为 AB． 因此 m 的取值范围是 4 5 ≤m≤ 4 5 ． 图 2 图 3 图 4 （3）设点 D 的坐标为 ))2)(2 1(,(  xxx ． ①如图 3，过点 A 作 BC 的平行线交抛物线于 D，过点 D 作 DE⊥x 轴于 E． 因为 OBCDAB  tantan ，所以 2 1 BO CO AE DE ．因此 2 1 2 1 )2)(2 1(    x xx ．解得 2 5x ．此时点 D 的坐标为 )2 3,2 5( ． 过 点 B 作 AC 的 平 行 线 交 抛 物 线 于 D ， 过 点 D 作 DF ⊥ x 轴 于 F ． 因 为 CAODBF  tantan ，所以 2 AO CO BF DF ．因此 22 )2)(2 1(   x xx ．解得 2 5x ．此 时点 D 的坐标为 )9,2 5( ． 综上所述，当 D 的坐标为 )2 3,2 5( 或 )9,2 5( 时，以 A、B、C、D 为顶点的四边形为直 角梯形． 考点伸展 第（3）题可以用代数的方法这样解：例如图 3，先求得直线 BC 为 12 1  xy ，再根 据 AD//BC 求得直线 AD 为 4 1 2 1  xy ，由直线 AD 和抛物线的解析式组成的方程组，得到 点 D 的坐标． 1.6 因动点产生的面积问题 例 1 如图 1，在平面直角坐标系中放置一直角三角板，其顶点为 A(0, 1)、B(2, 0)、 O(0, 0)，将此三角板绕原点 O 逆时针旋转 90°，得到三角形 A′B′O． （1）一抛物线经过点 A′、B′、B，求该抛物线的解析式； （2）设点 P 是第一象限内抛物线上的一个动点，是否存在点 P，使四边形 PB′A′B 的面 积是△A′B′O 面积的 4 倍？若存在，请求出点 P 的坐标；若不存在，请说明理由； （3）在（2）的条件下，试指出四边形 PB′A′B 是哪种形状的四边形？并写出它的两条 性质． 图 1 解答 （1）△AOB 绕着原点 O 逆时针旋转 90°，点 A′、B′的坐标分别为(－1, 0) 、(0, 2)． 因为抛物线与 x 轴交于 A′(－1, 0)、B(2, 0)，设解析式为 y＝a(x＋1)(x－2)， 代入 B′(0, 2)，得 a＝1． 所以该抛物线的解析式为 y＝－(x＋1)(x－2) ＝－x2＋x＋2． （2）S△A′B′O＝1． 如果 S 四边形 PB′A′B＝4 S△A′B′O＝4，那么 S 四边形 PB′OB＝3 S△A′B′O＝3． 如图 2，作 PD⊥OB，垂足为 D． 设点 P 的坐标为 (x，－x2＋x＋2)． 2 3 2 ' 1 1 1 1( ' ) (2 2) 22 2 2 2PB ODS DO B O PD x x x x x x         梯形 ． 2 3 21 1 1 3(2 )( 2) 22 2 2 2PDBS DB PD x x x x x           ． 所以 2 ' ' ' 2 +2PDBPB A D PB ODS S S x x    四边形 梯形 ． 解方程－x2＋2x＋2＝3，得 x1＝x2＝1． 所以点 P 的坐标为(1，2)． 图 2 图 3 图 4 （3）如图 3，四边形 PB′A′B 是等腰梯形，它的性质有：等腰梯形的对角线相等；等腰 梯形同以底上的两个内角相等；等腰梯形是轴对称图形，对称轴是经过两底中点的直线． 考点伸展 第（2）题求四边形 PB′OB 的面积，也可以如图 4 那样分割图形，这样运算过程更简单． ' 1 1' 22 2PB O PS B O x x x      ． 2 21 1 2( 2) 22 2PBO PS BO y x x x x            ． 所以 2 '' ' 2 +2PB O PBOPB A DS S S x x     四边形 ． 甚至我们可以更大胆地根据抛物线的对称性直接得到点 P： 作△A′OB′关于抛物线的对称轴对称的△BOE，那么点 E 的坐标为(1，2)． 而矩形 EB′OD 与△A′OB′、△BOP 是等底等高的，所以四边形 EB′A′B 的面积是△A′B′O 面积的 4 倍．因此点 E 就是要探求的点 P． 例 2 如图 1，在平面直角坐标系中，直线 1 12y x  与抛物线 y＝ax2＋bx－3 交于 A、 B 两点，点 A 在 x 轴上，点 B 的纵坐标为 3．点 P 是直线 AB 下方的抛物线上的一动点（不 与点 A、B 重合），过点 P 作 x 轴的垂线交直线 AB 于点 C，作 PD⊥AB 于点 D． （1）求 a、b 及 sin∠ACP 的值； （2）设点 P 的横坐标为 m． ①用含 m 的代数式表示线段 PD 的长，并求出线段 PD 长的最大值； ②连结 PB，线段 PC 把△PDB 分成两个三角形，是否存在适合的 m 的值，使这两个三 角形的面积比为 9∶10？若存在，直接写出 m 的值；若不存在，请说明理由． 图 1 解答 （1）设直线 1 12y x  与 y 轴交于点 E，那么 A(－2,0)，B(4,3)，E(0,1)． 在 Rt△AEO 中，OA＝2，OE＝1，所以 5AE  ．所以 2 5sin 5AEO  ． 因为 PC//EO，所以∠ACP＝∠AEO．因此 2 5sin 5ACP  ． 将 A(－2,0)、B(4,3)分别代入 y＝ax2＋bx－3，得 4 2 3 0, 16 4 3 3. a b a b        解得 1 2a  ， 1 2b   ． （2）由 21 1( , 3)2 2P m m m  ， 1( , 1)2C m m  ， 得 2 21 1 1 1( 1) ( 3) 42 2 2 2PC m m m m m         ． 所以 2 22 5 2 5 1 5 9 5sin ( 4) ( 1)5 5 2 5 5PD PC ACP PC m m m           ． 所以 PD 的最大值为 9 5 5 ． （3）当 S△PCD∶S△PCB＝9∶10 时， 5 2m  ； 当 S△PCD∶S△PCB＝10∶9 时， 32 9m  ． 图 2 考点伸展 第（3）题的思路是：△PCD 与△PCB 是同底边 PC 的两个三角形，面积比等于对应高 DN 与 BM 的比． 而 25 2 5 1 1cos cos ( 4) ( 2)( 4)5 5 2 5DN PD PDN PD ACP m m m m             ， BM＝4－m． ①当 S△PCD∶S△PCB＝9∶10 时， 1 9( 2)( 4) (4 )5 10m m m     ．解得 5 2m  ． ②当 S△PCD∶S△PCB＝10∶9 时， 1 10( 2)( 4) (4 )5 9m m m     ．解得 32 9m  ． 例 3 如图 1，直线 l 经过点 A(1，0)，且与双曲线 my x  (x＞0)交于点 B(2，1)．过点 ( , 1)P p p  (p＞1)作 x 轴的平行线分别交曲线 my x  (x＞0)和 my x   (x＜0)于 M、N 两点． （1）求 m 的值及直线 l 的解析式； （2）若点 P 在直线 y＝2 上，求证：△PMB∽△PNA； （3）是否存在实数 p，使得 S△AMN＝4S△AMP？若存在，请求出所有满足条件的 p 的值； 若不存在，请说明理由． 图 1 解答 （1）因为点 B(2，1)在双曲线 my x  上，所以 m＝2．设直线 l 的解析式为 y kx b  ， 代入点 A(1，0)和点 B(2，1)，得 0, 2 1. k b k b      解得 1, 1. k b     所以直线 l 的解析式为 1y x  ． （2）由点 ( , 1)P p p  (p＞1)的坐标可知，点 P 在直线 1y x  上 x 轴的上方．如图 2， 当 y＝2 时，点 P 的坐标为(3，2)．此时点 M 的坐标为(1，2)，点 N 的坐标为(－1，2)． 由 P(3，2)、M(1，2)、B(2，1)三点的位置关系，可知△PMB 为等腰直角三角形． 由 P(3，2)、N(－1，2)、A(1，0)三点的位置关系，可知△PNA 为等腰直角三角形． 所以△PMB∽△PNA． 图 2 图 3 图 4 （3）△AMN 和△AMP 是两个同高的三角形，底边 MN 和 MP 在同一条直线上． 当 S△AMN＝4S△AMP 时，MN＝4MP． ①如图 3，当 M 在 NP 上时，xM－xN＝4(xP－xM)．因此 2 2 2( ) 4 ( 1)xx x x               ．解 得 1 13 2x  或 1 13 2x  （此时点 P 在 x 轴下方，舍去）．此时 1 13 2p  ． ② 如 图 4 ， 当 M 在 NP 的 延 长 线 上 时 ， xM － xN ＝ 4(xM － xP) ． 因 此 2 2 2( ) 4 ( 1)xx x x               ．解得 1 5 2x  或 1 5 2x  （此时点 P 在 x 轴下方，舍去）．此 时 1 5 2p  ． 考点伸展 在本题情景下，△AMN 能否成为直角三角形？ 情形一，如图 5，∠AMN＝90°，此时点 M 的坐标为（1，2），点 P 的坐标为（3，2）． 情形二，如图 6，∠MAN＝90°，此时斜边 MN 上的中线等于斜边的一半． 不存在∠ANM＝90°的情况． 图 5 图 6 例 4 如图 1，在平面直角坐标系 xOy 中，直角梯形 OABC 的顶点 O 为坐标原点， 顶点 A、C 分别在 x 轴、y 轴的正半轴上，CB∥OA，OC＝4，BC＝3，OA＝5，点 D 在边 OC 上，CD＝3，过点 D 作 DB 的垂线 DE，交 x 轴于点 E． （1）求点 E 的坐标； （2）二次函数 y＝－x2＋bx＋c 的图象经过点 B 和点 E． ①求二次函数的解析式和它的对称轴； ②如果点 M 在它的对称轴上且位于 x 轴上方，满足 S△CEM＝2S△ABM，求点 M 的坐标． 图 1 解答 （1）因为 BC∥OA，所以 BC⊥CD．因为 CD＝CB＝3，所以△BCD 是等腰直角三角形．因 此∠BCD＝45°．又因为 BC⊥CD，所以∠ODE＝45°．所以△ODE 是等腰直角三角形， OE＝OD＝1．所以点 E 的坐标是（1，0）． （2）①因为抛物线 y＝－x2＋bx＋c 经过点 B（3，4）和点 E（ 1，0），所以 9 3 4, 1 0. b c b c         解得 6, 5. b c     所以二次函数的解析式为 y＝－x2＋6x－5，抛物线的对称轴为直线 x＝3． ②如图 2，如图 3，设抛物线的对称轴与 x 轴交于点 F，点 M 的坐标为（3，t）． CEM MEF COEOFMCS S S S    梯形 1 1 1(4 ) 3 2 1 4 42 2 2 2 tt t           ． （ⅰ）如图 2，当点 M 位于线段 BF 上时， ttS ABM  42)4(2 1 ．解方程 )4(242 tt  ，得 5 8t ．此时点 M 的坐标为（3， 5 8 ）． （ⅱ）如图 3，当点 M 位于线段 FB 延长线上时， 42)4(2 1  ttS ABM ．解方 程 )4(242  tt ，得 8t ．此时点 M 的坐标为（3，8）． 图 2 图 3 考点伸展 对于图 2，还有几个典型结论： 此时，C、M、A 三点在同一条直线上；△CEM 的周长最小． 可以求得直线 AC 的解析式为 4 45y x   ，当 x＝3 时， 8 5y  ．因此点 M（3， 5 8 ） 在直线 AC 上．因为点 A、E 关于抛物线的对称轴对称，所以 ME＋MC＝MA＋MC． 当 A、M、C 三点共线时，ME＋MC 最小，△CEM 的周长最小． 例 5 如图 1，四边形 OABC 是矩形，点 A、C 的坐标分别为(3,0)，(0,1)．点 D 是线 段 BC 上的动点（与端点 B、C 不重合），过点 D 作直线 1 2y x b   交折线 OAB 于点 E． （1）记△ODE 的面积为 S，求 S 与 b 的函数关系式； （2）当点 E 在线段 OA 上时，若矩形 OABC 关于直线 DE 的对称图形为四边形 O1A1B1C1， 试探究四边形 O1A1B1C1 与矩形 OABC 的重叠部分的面积是否发生变化？若不变，求出重叠 部分的面积；若改变，请说明理由． 图 1 解答 (1)①如图 2，当 E 在 OA 上时，由 1 2y x b   可知，点 E 的坐标为(2b,0)，OE＝2b．此 时 S＝S△ODE＝ 1 1 2 12 2OE OC b b     ． ②如图 3，当 E 在 AB 上时，把 y＝1 代入 1 2y x b   可知，点 D 的坐标为(2b－2,1)， CD＝2b－2，BD＝5－2b．把 x＝3 代入 1 2y x b   可知，点 E 的坐标为 3(3, )2b  ，AE ＝ 3 2b  ，BE＝ 5 2 b ．此时 S＝S 矩形 OABC－S△OAE－ S△BDE －S△OCD ＝ 1 3 1 5 13 3( ) ( )(5 2 ) 1 (2 2)2 2 2 2 2b b b b          2 5 2b b   ． (2)如图 4，因为四边形 O1A1B1C1 与矩形 OABC 关于直线 DE 对称，因此 DM＝DN，那 么重叠部分是邻边相等的平行四边形，即四边形 DMEN 是菱形． 作 DH⊥OA，垂足为 H．由于 CD＝2b－2，OE＝2b，所以 EH＝2． 设菱形 DMEN 的边长为 m．在 Rt△DEH 中，DH＝1，NH＝2－m，DN＝m，所以 12＋(2 －m)2＝m2．解得 5 4m  ．所以重叠部分菱形 DMEN 的面积为 5 4 ． 图 2 图 3 图 4 考点伸展 把本题中的矩形 OABC 绕着它的对称中心旋转，如果重叠部分的形状是菱形（如图 5）， 那么这个菱形的最小面积为 1，如图 6 所示；最大面积为 5 3 ，如图 7 所示． 图 5 图 6 图 7 例 6 如图 1，在△ABC 中，∠C＝90°，AC＝3，BC＝4，CD 是斜边 AB 上的高， 点 E 在斜边 AB 上，过点 E 作直线与△ABC 的直角边相交于点 F，设 AE＝x，△AEF 的面积 为 y． （1）求线段 AD 的长； （2）若 EF⊥AB，当点 E 在斜边 AB 上移动时， ①求 y 与 x 的函数关系式（写出自变量 x 的取值范围）； ②当 x 取何值时，y 有最大值？并求出最大值． （3）若点 F 在直角边 AC 上（点 F 与 A、C 不重合），点 E 在斜边 AB 上移动，试问， 是否存在直线 EF 将△ABC 的周长和面积同时平分？若存在直线 EF，求出 x 的值；若不存 在直线 EF，请说明理由． 图 1 备用图 解答 (1) 在 Rt △ ABC 中 ， AC ＝ 3 ， BC ＝ 4 ， 所 以 AB ＝ 5 ． 在 Rt △ ACD 中 ， 3 9cos 3 5 5AD AC A    ． (2) ①如图 2，当 F 在 AC 上时， 90 5x  ．在 Rt△AEF 中， 4tan 3EF AE A x  ．所 以 21 2 2 3y AE EF x   ． 如图 3，当 F 在 BC 上时，9 55 x ≤ ．在 Rt△BEF 中， 3tan (5 )4EF BE B x   ．所 以 21 3 15 2 8 8y AE EF x x     ． ②当 90 5x  时， 22 3y x 的最大值为 54 25 ； 当 9 55 x ≤ 时， 23 15 8 8y x x   23 5 75)8 2 32x   ( 的最大值为 75 32 ． 因此，当 5 2x  时，y 的最大值为 75 32 ． 图 2 图 3 图 4 (3)△ABC 的周长等于 12，面积等于 6． 先假设 EF 平分△ABC 的周长，那么 AE＝x，AF＝6－x，x 的变化范围为 3＜x≤5．因 此 1 1 4 2sin (6 ) ( 6)2 2 5 5AEFS AE AF A x x x x          ．解方程 2 ( 6) 35 x x   ，得 13 62x   ． 因为 13 62x   在 3≤x≤5 范围内（如图 4），因此存在直线 EF 将△ABC 的周长和面 积同时平分． 考点伸展 如果把第（3）题的条件“点 F 在直角边 AC 上”改为“点 F 在直角边 BC 上”，那么就 不存在直线 EF 将△ABC 的周长和面积同时平分． 先假设 EF 平分△ABC 的周长，那么 AE＝x，BE＝5－x，BF＝x＋1． 因此 21 1 3 3sin (5 )( 1) ( 4 5)2 2 5 10BEFS BE BF B x x x x            ． 解方程 23 ( 4 5) 310 x x    ．整理，得 2 4 5 0x x   ．此方程无实数根． 例 7 如图 1，正方形 ABCD 中，点 A、B 的坐标分别为（0，10），（8，4），点 C 在 第一象限．动点 P 在正方形 ABCD 的边上，从点 A 出发沿 A→B→C→D 匀速运动，同时动 点 Q 以相同速度在 x 轴上运动，当 P 点到 D 点时，两点同时停止运动，设运动的时间为 t 秒． （1）当 P 点在边 AB 上运动时，点 Q 的横坐标 x （长度单位）关于运动时间 t（秒）的 函数图象如图 2 所示，请写出点 Q 开始运动时的坐标及点 P 运动速度； （2）求正方形边长及顶点 C 的坐标； （3）在（1）中当 t 为何值时，△OPQ 的面积最大，并求此时 P 点的坐标． （4）如果点 P、Q 保持原速度速度不变，当点 P 沿 A→B→C→D 匀速运动时，OP 与 PQ 能否相等，若能，写出所有符合条件的 t 的值；若不能，请说明理由． 图 1 图 2 解答 （1） Q (1,0)，点 P 每秒钟运动 1 个单位长度． （2）过点 B 作 BE⊥y 轴于点 E，过点 C 作 x 轴的垂线交直线 BE 于 F，交 x 轴于 H． 在 Rt△ABE 中，BE＝8，AE＝10－4＝6，所以 AB＝10．由△ABE≌△BCF，知 BF＝AE ＝4，CF＝BE＝6．所以 EF＝8＋6＝14，CH＝8＋4＝12．因此点 C 的坐标为（14，12）． （3）过点 P 作 PM⊥y 轴于 M，PN⊥ x 轴于 N．因为 PM//BE，所以 AP AM MP AB AF BF   ， 即 10 6 8 t AM MP  ．因此 3 4,5 5AM t PM t  ．于是 3 410 ,5 5PN OM t ON PM t     ． 设△OPQ 的面积为 S (平方单位)，那么 21 1 3 3 47(1 )(10 ) 52 2 5 10 10S OQ PN t t t t          ， 定义域为 0≤ t ≤10． 因为抛物线开口向下，对称轴为直线 47 6t  ，所以当 47 6t  时，△OPQ 的面积最大．此 时 P 的坐标为( 94 15 ， 53 10 )． （4）当 5 3t  或 295 13t  时, OP 与 PQ 相等． 图 3 图 4 考点伸展 附加题的一般思路是：点 Q 的横坐标是点 P 的横坐标的 2 倍．先求直线 AB、BC、CD 的解析式，根据直线的解析式设点 P 的坐标，再根据两点间的距离公式列方程 PO＝PQ． 附加题也可以这样解： ①如图 4，在 Rt△AMP 中，设 AM＝3m，MP＝4 m，AP＝5m，那么 OQ＝8m．根据 AP、 OQ 的长列方程组 5 , 8 1 , m t m t     解得 5 3t  ． ②如图 5，在 Rt△GMP 中，设 GM＝3m，MP＝4 m，GP＝5m，那么 OQ＝8m．在 Rt△ GAD 中，GD＝7.5．根据 GP、OQ 的长列方程组 5 37.5 , 8 1 , m t m t      解得 295 13t  ． ③如图 6，设 MP＝4m，那么 OQ＝8m．根据 BP、OQ 的长列方程组 5 10 10, 8 1 , m t m t       解得 5 3t  ，但这时点 P 不在 BC 上． 图 5 图 6 1.7 因动点产生的相切问题 例 1 如图 1，A(－5,0)，B(－3,0)，点 C 在 y 轴的正半轴上，∠CBO＝45°，CD//AB， ∠CDA＝90°．点 P 从点 Q(4,0)出发，沿 x 轴向左以每秒 1 个单位长的速度运动，运动时间 为 t 秒． （1）求点 C 的坐标； （2）当∠BCP＝15°时，求 t 的值； （3）以点 P 为圆心，PC 为半径的⊙P 随点 P 的运动而 变化，当⊙P 与四边形 ABCD 的边（或边所在的直线）相切 时，求 t 的值． 图 1 动感体验 请打开几何画板文件名“12 河北 25”，拖动圆心 P 在点 Q 左侧运动，可以体验到，⊙P 可以与直线 BC、直线 DC、直线 AD 相切，不能与直线 AB 相切． 答案 （1）点 C 的坐标为(0,3)． （2）如图 2，当 P 在 B 的右侧，∠BCP＝15°时，∠PCO＝30°， 4 3t   ； 如图 3，当 P 在 B 的左侧，∠BCP＝15°时，∠CPO＝30°， 4 3 3t   ． 图 2 图 3 （3）如图 4，当⊙P 与直线 BC 相切时，t＝1； 如图 5，当⊙P 与直线 DC 相切时，t＝4； 如图 6，当⊙P 与直线 AD 相切时，t＝5.6． 图 4 图 5 图 6 例 2 如图 1，菱形 ABCD 的边长为 2 厘米，∠DAB＝60°．点 P 从 A 出发，以每秒 3 厘米的速度沿 AC 向 C 作匀速运动；与此同时，点 Q 也从点 A 出发，以每秒 1 厘米的速度沿射线作匀速运动．当点 P 到达点 C 时，P、Q 都停止运动．设点 P 运动的时间为 t 秒． （1）当 P 异于 A、C 时，请说明 PQ//BC； （2）以 P 为圆心、PQ 长为半径作圆，请问：在整个运动过 程中，t 为怎样的值时，⊙P 与边 BC 分别有 1 个公共点和 2 个公 共点？ 图一 答案 （1）因为 2 AQ t AB  ， 3 22 3 AP t t AC   ，所以 AQ AP AB AC  ．因此 PQ//BC． （2）如图 2，由 PQ＝PH＝ 1 2 PC ，得 1 (2 3 3 )2t t  ．解得 4 3 6t   ． 如图 3，由 PQ＝PB，得等边三角形 PBQ．所以 Q 是 AB 的中点，t＝1． 如图 4，由 PQ＝PC，得 2 3 3t t  ．解得 3 3t   ． 如图 5，当 P、C 重合时，t＝2． 因此，当 4 3 6t   或 1＜t≤3 3 或 t＝2 时，⊙P 与边 BC 有 1 个公共点． 当 4 3 6 ＜t≤1 时，⊙P 与边 BC 有 2 个公共点． 图 2 图 3 图 4 图 5 1.8 因动点产生的线段和差问题 例 1 如图 1，在平面直角坐标系中，抛物线 y＝ax2＋bx＋c 经过 A(－2, －4 )、O(0, 0)、 B(2, 0)三点． （1）求抛物线 y＝ax2＋bx＋c 的解析式； （2）若点 M 是该抛物线对称轴上的一点，求 AM＋OM 的最小值． 图 1 答案 （1） 21 2y x x   。 （2）AM＋OM 的最小值为 4 2 ． 图 2 图 3 例 2 如图 1，在平面直角坐标系中，抛物线 y＝－x2＋2x＋3 与 x 轴交于 A、B 两点， 与 y 轴交于点 C，点 D 是抛物线的顶点． （1）求直线 AC 的解析式及 B、D 两点的坐标； （2）点 P 是 x 轴上的一个动点，过 P 作直线 l//AC 交抛物线于点 Q．试探究：随着点 P 的运动，在抛物线上是否存在点 Q，使以 A、P、Q、C 为顶点的四边形是平行四边形？若存 在，请直接写出符合条件的点 Q 的坐标；若不存在，请说明理由； （3）请在直线 AC 上找一点 M，使△BDM 的周长最小，求出点 M 的坐标． 图 1 解答 （1）由 y＝－x2＋2x＋3＝－(x＋1)(x－3)＝－(x－1)2＋4， 得 A(－1, 0)、B(3, 0)、C(0, 3)、D(1, 4)． 直线 AC 的解析式是 y＝3x＋3． （2）Q1(2, 3)，Q2(1 7, 3  )，Q3(1 7, 3  )． （3）设点 B 关于直线 AC 的对称点为 B′，联结 BB′交 AC 于 F． 联结 B′D，B′D 与交 AC 的交点就是要探求的点 M． 作 B′E⊥x 轴于 E，那么△BB′E∽△BAF∽△CAO． 在 Rt△BAF 中， 1 3 10 AF BF AB  ，AB＝4，所以 12 10 BF  ． 在 Rt△BB′E 中， ' ' 1 3 10 B E BE BB  ， 24' 2 10 BB BF  ，所以 12' 5B E  ， 36 5BE  ． 所以 36 2135 5OE BE OB     ．所以点 B′的坐标为 21 12( , )5 5  ． 因为点 M 在直线 y＝3x＋3 上，设点 M 的坐标为(x, 3x＋3)． 由 ' ' ' ' ' ' DD MM B D B M  ，得 ' ' ' ' yD yB yM yB xD xB xM xB    ．所以 12 124 3 35 5 21 211 5 5 x x       ． 解得 9 35x  ．所以点 M 的坐标为 9 132( , )35 35 ． 图 2 图 3 考点伸展 第（2）题的解题思路是这样的： ①如图 4，当 AP 是平行四边形的边时，CQ//AP，所以点 C、Q 关于抛物线的对称轴对 称，点 Q 的坐标为(2, 3)． ②如图 5，当 AP 是平行四边形的对角线时，点 C、Q 分居 x 轴两侧，C、Q 到 x 轴的距 离相等． 解方程－x2＋2x＋3＝－3，得 1 7x   ．所以点 Q 的坐标为(1 7, 3  )或 (1 7, 3  )． 图 4 图 5 第二部分 函数图象中点的存在性问题 2.1 由比例线段产生的函数关系问题 例 1 在 Rt△ABC 中，∠C＝90°，AC＝6， 5 3sin B ，⊙B 的半径长为 1，⊙B 交边 CB 于点 P，点 O 是边 AB 上的动点． （1）如图 1，将⊙B 绕点 P 旋转 180°得到⊙M，请判断⊙M 与直线 AB 的位置关系； （2）如图 2，在（1）的条件下，当△OMP 是等腰三角形时，求 OA 的长； （3）如图 3，点 N 是边 BC 上的动点，如果以 NB 为半径的⊙N 和以 OA 为半径的⊙O 外切，设 NB＝y，OA＝x，求 y 关于 x 的函数关系式及定义域． 图 1 图 2 图 3 解答 （1） 在 Rt△ABC 中，AC＝6， 5 3sin B ， 所以 AB＝10，BC＝8． 过点 M 作 MD⊥AB，垂足为 D． 在 Rt△BMD 中，BM＝2， 3sin 5 MDB BM   ，所以 6 5MD  ． 因 此 MD ＞ MP ， ⊙ M 与 直 线 AB 相 离． 图 4 （2）①如图 4，MO≥MD＞MP，因此不存在 MO＝MP 的情况． ②如图 5，当 PM＝PO 时，又因为 PB＝PO，因此△BOM 是直角三角形． 在 Rt△BOM 中，BM＝2， 4cos 5 BOB BM   ，所以 8 5BO  ．此时 42 5OA  ． ③如图 6，当 OM＝OP 时，设底边 MP 对应的高为 OE． 在 Rt△BOE 中，BE＝ 3 2 ， 4cos 5 BEB BO   ，所以 15 8BO  ．此时 65 8OA  ． 图 5 图 6 （3）如图 7，过点 N 作 NF⊥AB，垂足为 F．联结 ON． 当两圆外切时，半径和等于圆心距，所以 ON＝x＋y． 在 Rt△BNF 中，BN＝y， 3sin 5B  ， 4cos 5B  ，所以 3 5NF y ， 4 5BF y ． 在 Rt△ONF 中， 410 5OF AB AO BF x y      ，由勾股定理得 ON2＝OF2＋NF2． 于是得到 2 2 24 3( ) (10 ) ( )5 5x y x y y     ． 整理，得 250 50 40 xy x   ．定义域为 0＜x＜5． 图 7 图 8 考点伸展 第（2）题也可以这样思考： 如图 8，在 Rt△BMF 中，BM＝2， 6 5MF  ， 8 5BF  ． 在 Rt△OMF 中，OF＝ 8 4210 5 5x x    ，所以 2 2 242 6( ) ( )5 5OM x   ． 在 Rt△BPQ 中，BP＝1， 3 5PQ  ， 4 5BQ  ． 在 Rt△OPQ 中，OF＝ 4 4610 5 5x x    ，所以 2 2 246 3( ) ( )5 5OP x   ． ①当 MO＝MP＝1 时，方程 2 242 6( ) ( ) 15 5x   没有实数根． ②当 PO＝PM＝1 时，解方程 2 246 3( ) ( ) 15 5x   ，可得 42 5x OA  ③当 OM＝OP 时，解方程 2 242 6( ) ( )5 5x  2 246 3( ) ( )5 5x   ，可得 65 8x OA  ． 例 2 如图 1，甲、乙两人分别从 A、B 两点同时出发，点 O 为坐标原点．甲沿 AO 方 向、乙沿 BO 方向均以每小时 4 千米的速度行走，t 小时后，甲到 达 M 点，乙到达 N 点． （1）请说明甲、乙两人到达点 O 前，MN 与 AB 不可能平行； （2）当 t 为何值时，△OMN∽△OBA？ （3）甲、乙两人之间的距离为 MN 的长．设 s＝MN2，求 s 与 t 之间 的函数 关系式， 并求甲 、乙两 人之间 距离的 最小 值． 图 1 答案 （1）当 M、N 都在 O 右侧时， 2 4 1 22 OM t tOA    ， 6 4 216 3 ON t tOB    ， 所以 OM ON OA OB  ．因此 MN 与 AB 不平行． （2）①如图 2，当 M、N 都在 O 右侧时，∠OMN＞∠B，不可能△OMN∽△OBA． ②如图 3，当 M 在 O 左侧、N 在 O 右侧时，∠MON＞∠BOA，不可能△OMN∽△OBA． ③如图 4，当 M、N 都在 O 左侧时，如果△OMN∽△OBA，那么 ON OA OM OB  ． 所以 4 6 2 4 2 6 t t   ．解得 t＝2． 图 2 图 3 图 4 （3）①如图 2， 2 4OM t  ， 1 2OH t  ， 3(1 2 )MH t  ． (6 4 ) (1 2 ) 5 2NH ON OH t t t        ． ②如图 3， 4 2OM t  ， 2 1OH t  ， 3(2 1)MH t  ． (6 4 ) (2 1) 5 2NH ON OH t t t        ． ③如图 4， 4 2OM t  ， 2 1OH t  ， 3(2 1)MH t  ． (2 1) (4 6) 5 2NH OH ON t t t        ． 综合①、②、③，s 2 2 2MN MH NH   2 2 2 23(2 1) (5 2 ) 16 32 28 16( 1) 12t t t t t            ． 所以当 t＝1 时，甲、乙两人的最小距离为 12 千米． 例 3 在 Rt△ABC 中，∠ACB＝90°，BC＝30，AB＝50．点 P 是 AB 边上任意一点， 直线 PE⊥AB，与边 AC 或 BC 相交于 E．点 M 在线段 AP 上，点 N 在线段 BP 上，EM＝EN， 12sin 13EMP  ． （1）如图 1，当点 E 与点 C 重合时，求 CM 的长； （2）如图 2，当点 E 在边 AC 上时，点 E 不与点 A、C 重合，设 AP＝x，BN＝y，求 y 关于 x 的函数关系式，并写出函数的定义域； （3）若△AME∽△ENB（△AME 的顶点 A、M、E 分别与△ENB 的顶点 E、N、B 对应）， 求 AP 的长． 图 1 图 2 备用图 解答 （1）在 Rt△ABC 中，BC＝30，AB＝50，所以 AC＝40， 3sin 5A  ， 3tan 4A  ． 在 Rt△ACP 中， 3sin 40 245CP AC A      ． 在 Rt△CMP 中，因为 12sin 13 CPCMP CM    ，所以 13 13 24 2612 12CM CP    ． （2）在 Rt△AEP 中， 3tan 4EP AP A x    ． 在 Rt△EMP 中，因为 12sin 13 EPEMP EM    ，所以 12tan 5 EPEMP MP    ． 因此 5 5 3 5 12 12 4 16MP EP x x    ， 13 13 3 13 12 12 4 16EM EP x x    ． 已知 EM＝EN，PE⊥AB，所以 MP＝NP 5 16 x ． 于是 5 2150 5016 16y BN AB AP NP x x x         ． 定义域为 0＜x＜32． （3）①如图 3，当 E 在 AC 上时，由 AM EN ME NB  ，得 5 13 16 16 13 215016 16 x x x x x    ． 解得 x＝AP＝22． ②如图 4，当 E 在 BC 上时，设 BP＝m，那么 AP＝50－m． 在 Rt△BEP 中， 4 3EP m ． 在 Rt△EMP 中， 5 5 4 5 12 12 3 9MP EP m m    ， 13 13 13412 12 9EM EP m m    ． 所以 5 1450 509 9AM AB BP MP m m m        ， 5 45 9 9BN BP NP m m m     ． 这时由 AM EN ME NB  ，得 14 1350 9 9 13 4 9 9 m m m m   ．解得 m＝BP＝8．所以 AP＝50－m＝42． 图 3 图 4 图 5 考点伸展 如果第（3）题没有条件“△AME 的顶点 A、M、E 分别与△ENB 的顶点 E、N、B 对应”， 那么还存在图 5 所示的一种情况，∠EAM＝∠EBN，此时 PE 垂直平分 AB，AP＝25． 2.2 由面积产生的函数关系问题 例 1 如图 1，抛物线 21 3 92 2y x x   与 x 轴交于 A、B 两点，与 y 轴交于点 C，联结 BC、AC． （1）求 AB 和 OC 的长； （2）点 E 从点 A 出发，沿 x 轴向点 B 运动（点 E 与点 A、B 不重合），过点 E 作 BC 的 平行线交 AC 于点 D．设 AE 的长为 m，△ADE 的面积为 s，求 s 关于 m 的函数关系式，并 写出自变量 m 的取值范围； （3）在（2）的条件下，联结 CE，求△CDE 面积的最大值；此时，求出以点 E 为圆心， 与 BC 相切的圆的面积（结果保留π）． 图 1 解答 （1）由 21 3 19 ( 3)( 6)2 2 2y x x x x      ，得 A(－3,0)、B(6,0)、C(0,－9)． 所以 AB＝9，OC＝9． （2）如图 2，因为 DE//CB，所以△ADE∽△ACB． 所以 2( )ADE ACB S AE S AB    ． 而 1 81 2 2ACBS AB OC    ，AE＝m， 所以 2 2 281 1( ) ( )9 2 2ADE ACB AE ms S S mAB       ． m 的取值范围是 0＜m＜9． 图 2 图 3 （3）如图 2，因为 DE//CB，所以 9CD BE m AD AE m   ． 因为△CDE 与△ADE 是同高三角形，所以 9CDE ADE S CD m S AD m     ． 所以 2 2 29 1 1 9 1 9 81( )2 2 2 2 2 8CDE mS m m m mm          ． 当 9 2m  时，△CDE 的面积最大，最大值为 81 8 ． 此时 E 是 AB 的中点， 9 2BE  ． 如图 3，作 EH⊥CB，垂足为 H． 在 Rt△BOC 中，OB＝6，OC＝9，所以 3 3 13sin 1313 B   ． 在 Rt△BEH 中， 9 3 13 27 13sin 2 13 26EH BE B     ． 当⊙E 与 BC 相切时， r EH ．所以 2 729 52S r   ． 考点伸展 在本题中，△CDE 与△BEC 能否相似？ 如图 2，虽然∠CED＝∠BCE，但是∠B＞∠BCA≥∠ECD，所以△CDE 与△BEC 不能 相似． 例 2 如图 1，图 2，在△ABC 中，AB＝13，BC＝14， 5cos 13ABC  ． 探究 如图 1，AH⊥BC 于点 H，则 AH＝_____，AC＝______，△ABC 的面积 S△ABC＝ ________． 拓展 如图 2，点 D 在 AC 上（可与点 A、C 重合），分别过点 A、C 作直线 BD 的垂线， 垂足为 E、F．设 BD＝x，AE＝m，CF＝n．（当点 D 与点 A 重合时，我们认为 S△ABD＝0） （1）用含 x，m 或 n 的代数式表示 S△ABD 及 S△CBD； （2）求(m＋n)与 x 的函数关系式，并求(m＋n)的最大值和最小值； （3）对给定的一个 x 值，有时只能确定唯一的点 D，指出这样的 x 的取值范围． 发现 请你确定一条直线，使得 A、B、C 三点到这条直线的距离之和最小（不必写出 过程），并写出这个最小值． 图 1 图 2 动感体验 请打开几何画板文件名“12 河北 26”，拖动点 D 由 A 向 C 运动，观察(m＋n)随 x 变化 的图象，可以体验到，D 到达 G 之前，(m＋n)的值越来越大；D 经过 G 之后，(m＋n)的值 越来越小．观察圆与线段 AC 的交点情况，可以体验到，当 D 运动到 G 时（如图 3），或者 点 A 在圆的内部时（如图 4），圆与线段 AC 只有唯一的交点 D． 图 3 图 4 答案 探究 AH＝12，AC＝15，S△ABC＝84． 拓展 （1）S△ABD＝ 1 2 mx ，S△CBD＝ 1 2 nx ． （2）由 S△ABC＝S△ABD＋S△CBD，得 1 1 842 2mx nx  ．所以 168m n x   ． 由于 AC 边上的高 56 5BG  ，所以 x 的取值范围是 56 5 ≤x≤14． 所以(m＋n)的最大值为 15，最小值为 12． （3）x 的取值范围是 x＝ 56 5 或 13＜x≤14． 发现 A、B、C 三点到直线 AC 的距离之和最小，最小值为 56 5 ． 例 3 如图 1，在 Rt△ABC 中，∠C＝90°，AC＝8，BC＝6，点 P 在 AB 上，AP＝ 2．点 E、F 同时从点 P 出发，分别沿 PA、PB 以每秒 1 个单位长度的速度向点 A、B 匀速运 动，点 E 到达点 A 后立刻以原速度沿 AB 向点 B 运动，点 F 运动到点 B 时停止，点 E 也随 之停止．在点 E、F 运动过程中，以 EF 为边作正方形 EFGH，使它与△ABC 在线段 AB 的 同侧．设 E、F 运动的时间为 t 秒(t＞0)，正方形 EFGH 与△ABC 重叠部分的面积为 S． （1）当 t＝1 时，正方形 EFGH 的边长是________；当 t＝3 时，正方形 EFGH 的边长 是________； （2）当 1＜t≤2 时，求 S 与 t 的函数关系式； （3）直接答出：在整个运动过程中，当 t 为何值时，S 最大？最大面积是多少？ 图 1 动感解答 （1）当 t＝1 时，EF＝2；当 t＝3 时，EF＝4． （2）①如图 1，当 60 11t＜ ≤ 时， 2EF t ．所以 24S t ． ②如图 2，当 6 6 11 5t＜ ≤ 时， 2EF EH t  ， 2AE t  ， 3 3 (2 )4 4NE AE t   ． 于是 3 11 32 (2 )4 4 2NH EH NE t t t       ， 21 1 4 2 2 2 3 3NHQS NH QH NH NH NH    △ 22 11 3 3 4 2t     ． 所以 2 2 22 11 3 25 11 34 3 4 2 24 2 2S t t t t          ． ③如图 3，当 6 25 t＜ ≤ 时， 4EF  ， 2AE t  ， 2AF t  ． 所以 2 23 3 38 8AFM AENS S S AF AE t    △ △ ． 图 2 图 3 图 4 （3）如图 4，图 5，图 6，图 7，重叠部分的最大面积是图 6 所示的六边形 EFNDQN， S 的最大值为1102 75 ，此时 146 25t  ． 图 5 图 6 图 7 考点伸展 第（2）题中 t 的临界时刻是这样求的： 如图 8，当 H 落在 AC 上时， 2AE t  ， 2EH EF t  ，由 2 3 2 4 t t  ，得 6 11t  ． 如图 9，当 G 落在 AC 上时， 2AF t  ， 2GF EF t  ，由 2 3 2 4 t t  ，得 6 5t  ． 图 8 图 9 例 4 如图 1，在平面直角坐标系中，四边形 OABC 是平行四边形．直线 l 经过 O、 C 两点，点 A 的坐标为(8，0)，点 B 的坐标为(11，4)，动点 P 在线段 OA 上从 O 出发以每 秒 1 个单位的速度向点 A 运动，同时动点 Q 从点 A 出发以每秒 2 个单位的速度沿 A→B→C 的方向向点 C 运动，过点 P 作 PM 垂直于 x 轴，与折线 O—C—B 相交于点 M．当 P、Q 两 点中有一点到达终点时，另一点也随之停止运动，设点 P、Q 运动的时间为 t 秒（t＞0），△ MPQ 的面积为 S． （1）点 C 的坐标为____________，直线 l 的解析式为____________； （2）试求点 Q 与点 M 相遇前 S 与 t 的函数关系式，并写出相应的 t 的取值范围． （3）试求题（2）中当 t 为何值时，S 的值最大？最大值是多少？ 图 1 解答 （1）点 C 的坐标为(3，4)，直线 l 的解析式为 4 3y x ． （2）①当 M 在 OC 上，Q 在 AB 上时， 50 2t＜ ≤ ． 在 Rt△OPM 中，OP＝t， 4tan 3OMP  ，所以 4 3PM t ． 在 Rt△AQE 中，AQ＝2t， 3cos 5QAE  ，所以 6 5AE t ． 于是 6 18 85 5PE t t t     ．因此 21 2 16 2 15 3S PE PM t t    ． ②当 M 在 OC 上，Q 在 BC 上时， 5 32 t＜ ≤ ． 因为 2 5BQ t  ，所以 11 (2 5) 16 3PF t t t      ． 因此 21 3222 3S PF PM t t     ． ③当 M、Q 相遇时，根据 P、Q 的路程和 2 11 5t t   ，解得 16 3t  ． 因此当 M、Q 都在 BC 上，相遇前， 163 3t＜ ≤ ，PM＝4， 16 2 16 3MQ t t t     ． 所以 1 6 322S MQ PM t     ． 图 2 图 3 图 4 （3）①当 50 2t＜ ≤ 时， 2 22 16 2 160( 20)15 3 15 3S t t t     ． 因为抛物线开口向上，在对称轴右侧，S 随 t 的增大而增大， 所以当 5 2t  时，S 最大，最大值为 85 6 ． ②当 5 32 t＜ ≤ 时， 2 232 8 1282 2( )3 3 9S t t t       ． 因为抛物线开口向下，所以当 8 3t  时，S 最大，最大值为128 9 ． ③当 163 3t＜ ≤ 时， 1 6 322S MQ PM t     ． 因为 S 随 t 的增大而减小，所以当 3t  时，S 最大，最大值为 14． 综上所述，当 8 3t  时，S 最大，最大值为128 9 ． 考点伸展 第（2）题中，M、Q 从相遇到运动结束，S 关于 t 的函数关系式是怎样的？ 此时16 13 3 2t＜ ≤ ， 2 16 3 16MQ t t t     ．因此 1 6 322S MQ PM t    ． 图 5 例 5 如图 1，矩形 ABCD 中，AB＝6，BC＝ 2 3 ，点 O 是 AB 的中点，点 P 在 AB 的延长线上，且 BP＝3．一动点 E 从 O 点出发，以每秒 1 个单位长度的速度沿 OA 匀速运 动，到达 A 点后，立即以原速度沿 AO 返回；另一动点 F 从 P 点出发，以每秒 1 个单位长 度的速度沿射线 PA 匀速运动，点 E、F 同时出发，当两点相遇时停止运动，在点 E、F 的运 动过程中，以 EF 为边作等边△EFG，使△EFG 和矩形 ABCD 在射线 PA 的同侧．设运动的 时间为 t 秒（t≥0）． （1）当等边△EFG 的边 FG 恰好经过点 C 时，求运动时间 t 的值； （2）在整个运动过程中，设等边△EFG 和矩形 ABCD 重叠部分的面积为 S，请直接写出 S 与 t 之间的函数关系 式和相应的自变量 t 的取值范围； （3）设 EG 与矩形 ABCD 的对角线 AC 的交点为 H， 是否存在这样的 t，使△AOH 是等腰三角形？若存在，求 出 对 应 的 t 的 值 ； 若 不 存 在 ， 请 说 明 理 由． 图 1 解答 （1）在 Rt△ABC 中， 2 3 3tan 6 3 BCBAC AB     ， 所以∠BAC＝30°． 如图 2，当等边△EFG 的边 FG 恰好经过点 C 时， 在 Rt△BCF 中，∠BFC＝60°，BC= 2 3 ， 所 以 BF ＝ 2 ． 因 此 PF ＝ 3 － 2 ＝ 1 ， 运 动 时 间 t ＝ 1． 图 2 （2）①如图 3，当 0≤t＜1 时，重叠部分为直角梯形 BCNE， 2 3 4 3S t  ． ②如图 4，当 1≤t＜3 时，重叠部分为五边形 BQMNE， 23 4 3 3 3S t t    ． ③如图 5，当 3≤t＜4 时，重叠部分为梯形 FMNE， 4 3 20 3S t   ． ④如图 6，当 4≤t＜6 时，重叠部分为等边三角形 EFG， 23( 6)S t  ． 图 3 图 4 图 5 （3）等腰△AOH 分三种情况：①AO＝AH，②OA＝OH，③HA＝HO． 在△AOH 中，∠A＝30°为定值，AO＝3 为定值，AH 是变化的． △AEH 的形状保持不变，AH＝ 3 AE．当 E 由 O 向 A 运动时，AE＝3－t；当 E 经 A 折返后，AE＝t－3． 图 6 图 7 图 8 ①当 AO＝AH 时，解 3(3 ) 3t  ，得 3 3t   （如图 7）； 解 3( 3) 3t   ，得 3 3t   （如图 8）． ②当 OA＝OH 时，∠AOH＝120°，点 O 与点 E 重合，t＝0（如图 9）． ③当 HA＝HO 时，H 在 AE 的垂直平分线上，AO＝ 3 AH＝3AE． 解3(3 ) 3t  ，得 t＝2（如图 10）；解3( 3) 3t   ，得 t＝4（如图 11）． 图 9 图 10 图 11 考点伸展 图 3，图 4 中，点 E 向 A 运动，EF＝6；图 5，图 6 中，点 E 折返，EF＝12－2t．