2014江苏徐州市数学中考试卷 12页

徐州市2014年初中毕业、升学考试 数学 ‎（满分150分，考试时间120分钟）‎ 一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案前的字母代号填涂在答题卡的相应位置）‎ ‎1．（2014江苏徐州， 1，3分）等于 A．2 B． C． D．‎ ‎【答案】C.‎ ‎2．（2014江苏徐州， 2，3分）右图是用5个相同的的立方块搭成的几何体，其主视图是 ‎【答案】D.‎ ‎3．（2014江苏徐州， 3，3分）抛掷一枚均匀的硬币，前两次都正面朝上，第3次正面朝上的概率 A．大于 B．等于 C．小于 D．无法确定 ‎【答案】B.‎ ‎4．（2014江苏徐州， 4，3分）下列运算中错误的是 A． B． C． D． ‎ ‎【答案】A.‎ ‎5．（2014江苏徐州， 5，3分）将函数的图像沿轴向上平移2个单位长度后，所得图像对应的函数关系式为 A． B． C． D． ‎ ‎【答案】A.‎ ‎6．（2014江苏徐州， 6，3分）顺次连接正六边形的的三个不相邻的顶点，得到如图所示的图形，该图形 A．既是轴对称图形也是中心对称图形 B．是轴对称图形但并不是中心对称图形 ‎ C．是中心对称图形但并不是轴对称图形 D．既不是轴对称图形也不是中心对称图形 ‎ ‎ ‎【答案】B.‎ ‎7．（2014江苏徐州， 7，3分）若顺次连接四边形的各边中点所得到的四边形是菱形，则该四边形一定是 A．矩形 B．等腰梯形 C．对角线相等的四边形 D．对角线互相垂直的四边形 ‎ ‎【答案】C.‎ ‎8．（2014江苏徐州， 8，3分）点A、B、C在同一条数轴上，其中A、B表示的数分别为、1．若BC=2，则AC等于 A．3 B．2 C．3或5 D．2或6 ‎ ‎【答案】D.‎ 二、填空题（本大题共10小题，每小题3分，满分18分，共30分，不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．（2014江苏徐州， 9，3分）函数中，自变量的取值范围为_____________．‎ ‎【答案】‎ ‎10．（2014江苏徐州， 10，3分）我国“钓鱼岛”周围海域面积约为170 000，该数用科学记数法可表示为_________．‎ ‎【答案】‎ ‎11．（2014江苏徐州， 11，3分）函数与的图象的交点坐标为_______________．‎ ‎【答案】‎ ‎12．（2014江苏徐州， 12，3分）若，，则代数式的值等于___________．‎ ‎【答案】2‎ ‎13．（2014江苏徐州， 13，3分）半径为4cm，圆心角为60°的扇形的面积为_____________．‎ ‎【答案】‎ ‎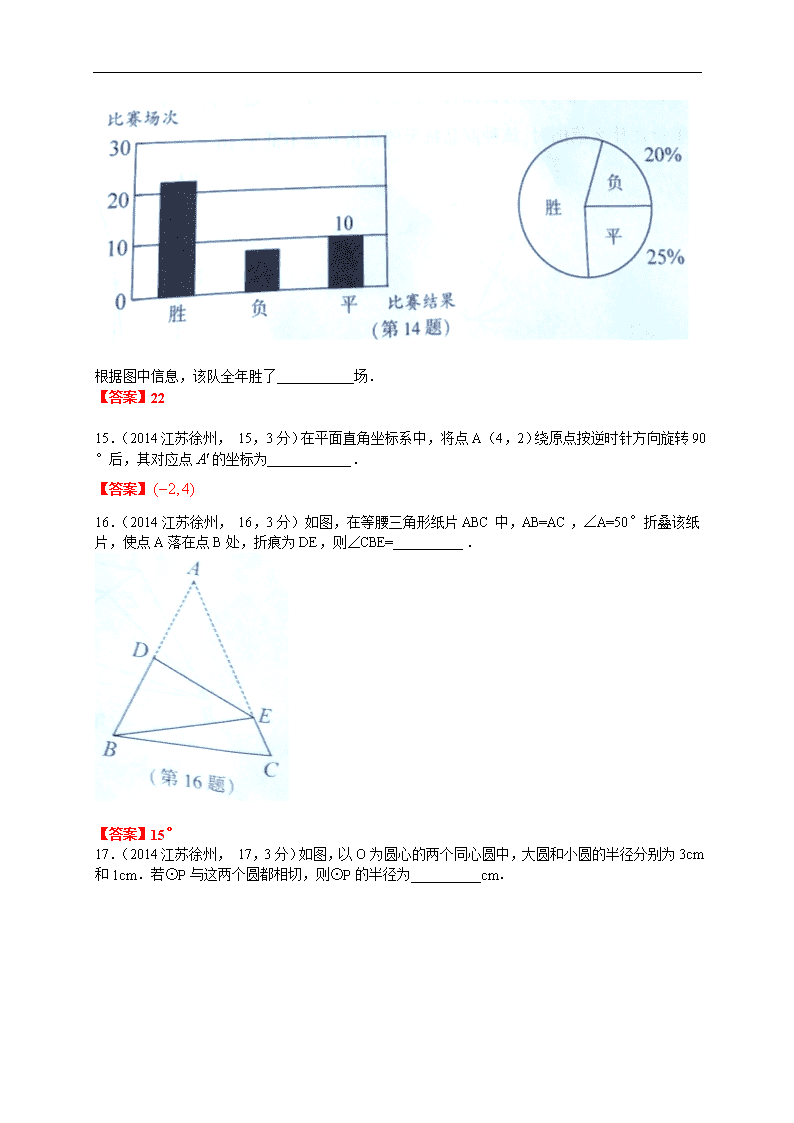14．（2014江苏徐州， 14，3分）下面是某足球队全年比赛情况的统计图：‎ 根据图中信息，该队全年胜了___________场．‎ ‎【答案】22‎ ‎15．（2014江苏徐州， 15，3分）在平面直角坐标系中，将点A（4，2）绕原点按逆时针方向旋转90°后，其对应点的坐标为____________．‎ ‎【答案】‎ ‎16．（2014江苏徐州， 16，3分）如图，在等腰三角形纸片ABC中，AB=AC，∠A=50°折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE=__________．‎ ‎【答案】15°‎ ‎17．（2014江苏徐州， 17，3分）如图，以O为圆心的两个同心圆中，大圆和小圆的半径分别为3cm和1cm．若⊙P与这两个圆都相切，则⊙P的半径为__________cm．‎ ‎【答案】1或2‎ ‎18．（2014江苏徐州， 18，3分）如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以的速度移动；同时，点Q沿边AB、BC从点A开始向点C以的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发 时，∆PAQ的面积为，与的函数图象如图②所示，则线段EF所在直线对应的函数关系式为__________________‎ ‎【答案】‎ 三、解答题（本大题共10小题，共86分，请在答题卡指定区域作答，解答时应写出说明、证明过程或演算步骤）‎ ‎19．（2014江苏徐州， 19①，5分）‎ ‎（1）计算：； ‎ ‎【答案】（1）解： ‎ ‎（2）（2014江苏徐州， 19②，5分）计算：‎ ‎【答案】解：‎ ‎ ‎ ‎20．（2014江苏徐州， 20①，5分）‎ ‎（1）解方程： ； ‎ ‎【答案】解： ‎ 或 ‎（2）（2014江苏徐州， 20②，5分）解不等式组：‎ ‎【答案】解：由①得： ‎ ‎ 由②得：‎ ‎， 不等式组的解集为：‎ ‎21．（2014江苏徐州， 21，7分）已知：如图，在□ABCD中，点E、F在AC上，且AE=CF．‎ 求证：四边形BEDF是平行四边形 证明：‎ 连接BD与AC相交于点O ‎∵四边形ABCD为平行四边形 ‎∴OB=OD，OA=OC ‎∵AE=CF ‎∴OE=OF ‎∴四边形BEDF是平行四边形 ‎22．（2014江苏徐州， 22，7分）甲、乙两人在5次打靶测试中命中的环数如下：‎ 甲：8，8，7，8，9；‎ 乙：5，9，7，10，9；‎ （1） 填表如下：‎ 平均数 众数 中位数 方差 甲 ‎8‎ ‎9‎ ‎8‎ ‎0.4‎ 乙 ‎8‎ ‎9‎ ‎9‎ ‎3.2‎ （2） 教练根据这5次的成绩，选择甲参加射击比赛，教练的理由是什么？‎ （3） 如果乙再射1次，命中8环，那么乙射击成绩的方差____________．（填“变大”、“变小”或“不变”）‎ ‎【答案】‎ 解：（1）如表所示 ‎ （2）理由：甲与乙的平均成绩相同，且甲的方差比较小，说明甲的成绩较乙来得稳定，故选甲；‎ ‎ （3）变小 ‎23．（2014江苏徐州， 23，8分）某学习班小组由3名男生和1名女生组成，在一次合作学习后，开始进行成果展示 ‎（1）如果随机选取1名同学单独展示，那么女生展示的概率为_________；‎ ‎（2）如果随机选取2名同学共同展示，求同为男生展示的概率．‎ ‎【答案】‎ 解：（1）‎ ‎（2）‎ 男1‎ 男2‎ 男3‎ 女 男1‎ 男1，男2‎ 男1，男3‎ 男1，女 男2‎ 男2，男1‎ 男2，男3‎ 男2，女 男3‎ 男3，男1‎ 男3，男2‎ 男3，女 女 女，男1‎ 女，男2‎ 女, 男3‎ 由表可知，共有9种情况，其中同时是男生的（记为事件A）共有6种情况，‎ ‎∴P（A）=‎ ‎24．（2014江苏徐州， 24，8分）几个小伙伴打算去音乐厅观看演出，他们准备用360元钱购买门票．下面是两个小伙伴的对话：‎ 根据对话中的信息，请你求出小伙伴们的人数．‎ ‎【答案】‎ 解：设共有个小伙伴，依题意得：‎ 解得：‎ ‎∵把代入 ‎∴为方程的解 答：共有8个小伙伴．‎ ‎25．（2014江苏徐州， 25，8分）如图，轮船从点A处出发，先航行至位于点A的南偏西15°且与点A相距100km的点B处，再航行至位于点B的北偏东75°且与点B相距200km的点C处．‎ ‎（1）求点C与点A的距离（精确到1km）；‎ ‎（2）确定点C相对于点A的方向．‎ ‎（参考数据：）‎ ‎【答案】‎ 解：‎ 依题意可得：∠B=60°，过点A作AD⊥BC，垂足为D ‎∵在RT⊿ABD中，AB=100‎ ‎∴，‎ ‎∵BC=200 ∴CD=150‎ ‎∴在RT⊿ACD中，‎ 即：∠C=30°‎ ‎∴∠BAC=90°‎ ‎∴，C在A的南偏东75°‎ ‎26．（2014江苏徐州， 26，8分）某种商品每天的销售利润（元）与销售单价（元）之间满足关系：其图象如图所示．‎ ‎（1）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？‎ ‎（2）销售单价在什么范围时，该种商品每天的销售利润不低于16元？‎ ‎【答案】‎ ‎（1）∵的图象经过点（5，0）、（7，16）‎ ‎∴ 解得：‎ 即：‎ ‎∴当销售价为10元时，最大利润为25元；‎ ‎（2）∵为抛物线的对称轴，且（7，16）在抛物线上 ‎∴（13，16）也在该抛物线上 ‎∴当时，销售利润不低于16．‎ ‎27．（2014江苏徐州， 27，10分）如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数的图象的两支上，且PB⊥轴于点C，PA⊥轴于点D，AB分别与轴、轴本交于点E、F．已知B（1，3）‎ ‎（1）；‎ ‎（2）试说明AE=BF；‎ ‎（3）当四边形ABCD的面积为时，求点P的坐标．‎ ‎【答案】‎ ‎（1）‎ ‎（2）∵B（1，3）‎ ‎∴设点P的坐标为（1，m）即：‎ ‎∴直线AB的解析式为：‎ ‎∴，‎ ‎∴，‎ 即：AE=BF ‎（3）∵，，，‎ ‎∴ 且∠P=∠P=90°‎ ‎∴∆PCD∽∆PBA ‎∴ 即：‎ ‎∴‎ ‎∴P（1，-2）‎ ‎28．（2014江苏徐州， 28，10分）如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动．以CE为直径作⊙O，点F为⊙O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与⊙O相交于点G，连接CG．‎ ‎（1）试说明四边形EFCG是矩形；‎ ‎（2）当⊙O与射线BD相切时，点E停止移动．在点E移动的过程中，‎ ‎①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；‎ ‎②求点G移动路线长．‎ ‎【答案】‎ 解：（1）∵CE为⊙O的直径 ‎ ∴∠CFE=∠CGE=90°‎ ‎ ∵EG⊥EF ‎ ∴∠GEF=90°‎ ‎ ∴四边形EFCG为矩形 ‎（2）①∵‎ ‎∴∠FCE=∠ADB ‎∴‎ 即：‎ ‎∴，‎ ‎∴‎ ‎∴当CE=AC=5时，；当CE=CD=3时，‎ ‎②如图，连接FG，且过点F、G作AD的垂线，垂足分别为P、Q ‎∵FP⊥AD ‎∴AB∥FP ‎∴∠DFP=∠DBA ‎∵∠GEF=90°‎ ‎∴FG为⊙O的直径 ‎∴∠FDG=90°‎ ‎∴∠DFP=∠GDQ ‎∴∠DBA=∠GDQ ‎∴‎ 即：‎ ‎∴点G的运动轨迹为一线段 当点F与点D重合时，EG与⊙O相切，FG为点G的移动路线长：‎