中考数学总复习专题基础知识回顾六方程与方程组 32页

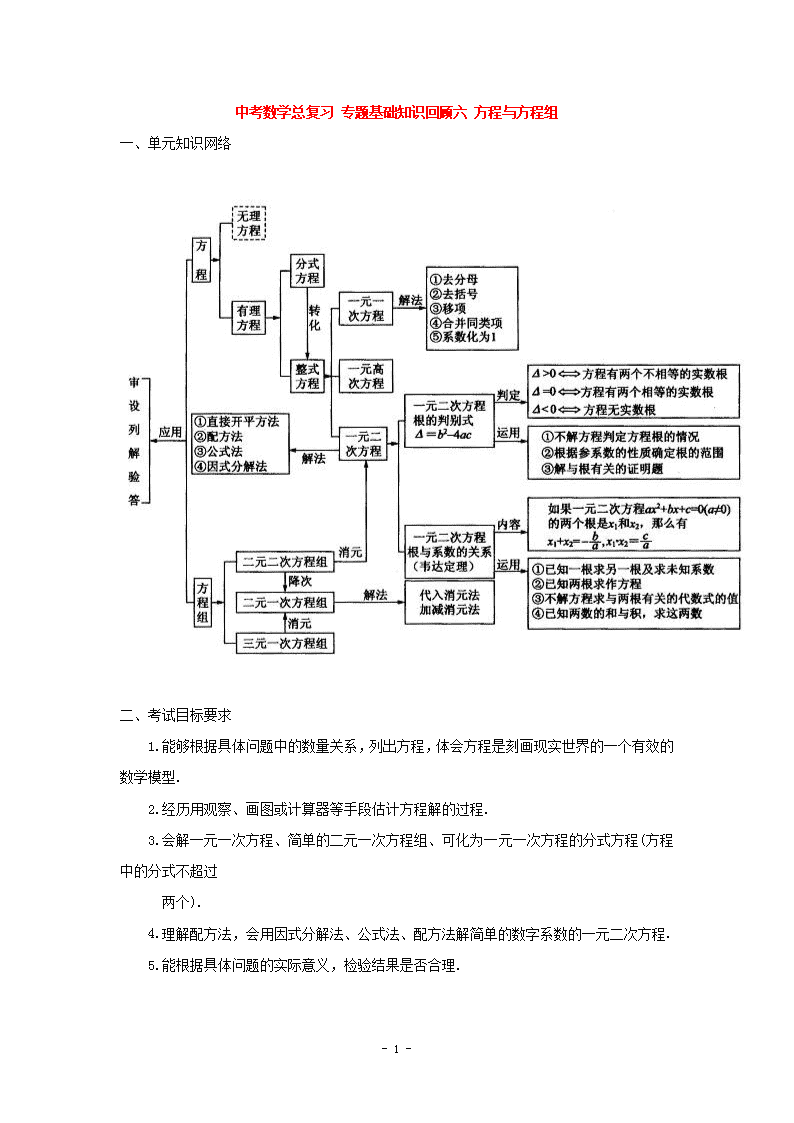
- 1 - 中考数学总复习 专题基础知识回顾六 方程与方程组 一、单元知识网络 　 二、考试目标要求 　　1.能够根据具体问题中的数量关系，列出方程，体会方程是刻画现实世界的一个有效的 数学模型. 　　2.经历用观察、画图或计算器等手段估计方程解的过程. 　　3.会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程(方程 中的分式不超过 　　　两个). 　　4.理解配方法，会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程. 　　5.能根据具体问题的实际意义，检验结果是否合理. - 2 - 三、知识考点梳理 考点一：等式性质 　　1.等式的两边都加上(或减去)同一个整式，结果仍是等式. 　　2.等式的两边都乘以同一个数，结果仍是等式. 　　3.等式的两边都除以同一个不等于零的数，结果仍是等式. 考点二：方程及相关概念 1.方程定义 　　含有未知数的等式叫做方程. 2.方程的解 　　使方程两边的值相等的未知数的值，叫做方程的解(一元方程的解也叫做根). 3.解方程 　　求方程的解的过程，叫做解方程. 考点三：一元一次方程 1.一元一次方程定义 　　只含有一个未知数，且未知数的次数是一次的整式方程叫做一元一次方程. 2.一元一次方程的一般形式: 　　 . 3.解一元一次方程的一般步骤： 　　(1)去分母；(2)去括号；(3)移项；(4)合并同类项；(5)系数化成 1；(6)检验(检验步 骤可以不写出来) 考点四：二元一次方程组 1.二元一次方程组定义 - 3 - 　　两个含有两个未知数，且未知数的次数是一次的整式方程组成的一组方程，叫做二元一 次方程组. 2.二元一次方程组的一般形式: 　　 3. 二元一次方程组的解法： 　　(1) 代入消元法； 　　(2) 加减消元法. 考点五：分式方程 1.分式方程定义 　　分母中含有未知数的方程叫做分式方程. 2.分式方程与整式方程的联系与区别： 　　分母中是否含有未知数. 3.分类: 　　(1)可化为一元一次方程的分式方程； 　　(2)可化为一元二次方程的分式方程. 4.解分式方程的一般步骤： 　　(1)去分母，化为整式方程： 　　　 ①把各分母分解因式； 　　　 ②找出各分母的最简公分母； 　　　 ③方程两边各项乘以最简公分母； 　　(2)解整式方程. 　　(3)检验(检验步骤必需写出来). 　　　 ①把未知数的值代入原方程(一般方法)；　　　②把未知数的值代入最简公分母(简 - 4 - 便方法). 　　(4)结论确定分式方程的解. 考点六：一元二次方程 1.一元二次方程定义 　　只含有一个未知数，且未知数的次数是二次的整式方程叫做一元二次方程. 2.一元二次方程的一般形式： 　　 . 3.一元二次方程的解法： 　　(1)配方法 　　1)通过配成完全平方式的形式来解一元二次方程的方法称为配方法. 　　2)用配方解方程的一般步骤: 　　　①化 1:把二次项系数化为 1(方程两边都除以二次项系数)； 　　　②移项:把常数项移到方程的右边； 　　　③配方:方程两边都加上一次项系数绝对值一半的平方； 　　　④变形:方程左边写成完全平方形式，右边合并同类； 　　　⑤开方:求平方根； 　　　⑥求解:解一元一次方程； 　　　⑦定解:写出原方程的解. 　　(2)公式法: 　　1)一元二次方程: 　　　当 时，它的根是 　　2)用求根公式解一元二次方程的方法称为公式法(solving by formular). 　　3)用公式法解题的一般步骤: 　　　①变形:化已知方程为一般形式； 　　　②确定系数:用 a，b，c 写出各项系数； - 5 - 　　　③计算: 的值； 　　　④代入:把有关数值代入公式计算； 　　　⑤定根:写出原方程的根. 　　(3)因式分解法: 　　1)当一元二次方程的一边是 0，而另一边易于分解成两个一次因式的乘积时，我们就可 以用分解因式的 　　　方法求解.这种用分解因式解一元二次方程的方法称为因式分解法. 　　2)因式分解法解一元二次方程的一般步骤是: 　　　①化方程为一般形式； 　　　②将方程左边因式分解； 　　　③根据“两个因式的积等于零，至少有一个因式为零”，转化为两个一元一次方程； 　　　④分别解两个一元一次方程，它们的根就是原方程的根. 考点七：一元二次方程根的判别式 　　我们知道:代数式 对于方程的根起着关键的作用. 　 　 当 时 ， 方 程 有 两 个 不 相 等 的 实 数 根 ； 　　当 时，方程 有两个相等的实数根 ； 　　当 时，方程 没有实数根. 　　所以我们把 叫做方程 的根的判别式，用“△”来表示， 即 　　 . 考点八：列方程(组)解应用题的一般步骤： 　　1.审:分析题意，找出已、未知之间的数量关系和相等关系. 　　2.设:选择恰当的未知数(直接或间接设元)，注意单位的统一和语言完整. - 6 - 　　3.列:根据数量和相等关系，正确列出代数式和方程(组). 　　4.解:解所列的方程(组). 　　5.验: (有三次检验 ①是否是所列方程(组)的解；②是否使代数式有意义；③是否满足 实际意义). 　　6.答:注意单位和语言完整. 四、规律方法指导 　　复习本专题时应抓住其实质：元和次，在定义上区分方程(组)的各种类型，并能够根据 定义具有的双重性解方程(组)和研究分式方程增根、失根情况.在解方程(组)时，把握住转 化的数学思想：化多元为一元，化高次为低次，化分式为整式；采取的手段是加减消元法、 代入消元法、因式分解法、换元降次法、去分母等方法；对于特殊形式的方程(组)可采取对 称思想、整体思想、非负数性质、定义法、拆项法等特殊方法求解.列方程(组)解应用题要 善于从社会关注的热点问题中寻找题中的等量关系. 经典例题透析 类型一：一元一次方程 　　 1．若 是关于 x 的一元一次方程，则 m 的值是( ) 　　A. 　　　　　B.-2　　　　　C.2　　　　　D.4 　　思路点拨：根据一元一次方程的定义，首先要满足未知项系数不为 0，其次未知项的最 高次数为 1. 　　解： 且 ，所以 . 　　举一反三： 　　【变式 1】关于 x 的一元一次方程 的解为__________. 　　思路点拨：根据一元一次方程的定义. 　　解析：原方程是一元一次方程，则有两种情况： 　　　　　(1)当 k-1=1，即 k=2 时，原方程为 3x+x-8=0，解之得 x=2； 　　　　　(2)当 且 时，也就是当 k=-1 时，原方程化为-2x-8=0，解之 得 x=-4； - 7 - 　　　　　所以原方程的解为 x=2 或 x=-4.故答案为 x=2 或 x=-4. 　　总结升华：运用一元一次方程的概念特征解题，可以从两个方面把握：其一是应用概念 的本质属性作出正确的判断；其二是在这一概念下，根据概念具备的本质特征得出相应的结 论(如本例中的 k-1=1 和 且 )，在解题过程中不断探索，实现解题目的. 　　 2．解方程： 　　(1) ；　　　　　(2) [ ( -1)-2]-2x=3. 　　思路点拨：(1)因为方程含有分母，应先去分母.注意每一项都要乘以 6； 　　　　　　　 (2)此方程含括号，因为 × =1，所以先去中括号简便. 　　解：(1)两边同时乘以 6，(去分母)得 　　　　　 3(x+1)=2x-(3x-1)-6x， 　　　　　 去括号，得 3x+3=2x-3x+1-6x 　　　　　 移项后整理，得 10x=-2，∴ . 　　　　(2)去中括号：( -1)- -2x=3 　　　　　 去小括号： -1- -2x=3 　　　　　 去分母：5x-20-24-40x=60 　　　　　 移项：5x-40x=60+44 　　　　　 合并同类项：-35x=104 　　　　　 系数化成 1 得：x=- . 　　总结升华：(1)去分母时，在方程的两边都乘以各分母的最小公倍数.要注意不要漏掉不 含分母的项；(2)去括号，按照去括号法则先去小括号，再去中括号，最后去大括号.特别注 意括号前是负号时，去掉负号和括号，括号里的各项都要变号.括号前有数字因数时要注意 使用分配律；(3)移项注意要改变性质符号；(4)技巧性解法的发现需要认真观察问题的结构 - 8 - 特征，需要突破习惯性思维的束缚. 　　举一反三： 　　【变式 1】解下列方程 　　(1)8-9x=9-8x；　　　　　　　　　 (2) ； 　　(3) ；　　　　(4) . 　　解：(1)8-9x=9-8x 　　　　　 -9x+8x=9-8 　　　　　 -x=1 　　　　　 x=-1 　　易错点关注：移项时忘了变号； 　　(2) 　　法一： 　　　　　4(2x-1)-3(5x+1)=24 　　　　　8x-4-15x-3=24 　　　　　-7x=31 　　　　　 　　易错点关注：两边同乘以各方面的最小公倍数，注意等号右边的单个数字 1 也要乘以 24； 注意去分母后的去括号问题，4(2x-1)错解为 8x-1，分配需逐项分配，-3(5x+1)化为-15x+3 忘了去括号变号； 　　法二：(就用分数算) 　　　　　 　　　　　 - 9 - 　　　　　 　　　　　 　　　　　 　　易错点关注：此处易错点是第一步拆分式时将 ，忽略此处有一 个括号前面是负号，去掉括号要变号的问题，即 ； 　　(3) 　　　 6x-3(3-2x)=6-(x+2) 　　　 6x-9+6x=6-x-2 　　　 12x+x=4+9 　　　 13x=13 　　　 x=1 　　易错点关注：两边同乘，每项均乘到，去括号注意变号； 　　(4) 　　　 2(4x-1.5)-5(5x-0.8)=10(1.2-x) 　　　 8x-3-25x+4=12-10x 　　　 8x-25x+10x=12+3-4 　　　 -7x=11 　　　 　　易错点关注：此题首先需面对分母中的小数，有同学会忘了小数运算的细则，不能发现 ，而是两边同乘以 0.5×0.2 进行去分母变形，更有思维跳跃的 同 学 错 认 为 0.5 × 0.2=1 ， 两 边 同 乘 以 1 ， 将 方 程 变 形 为 ： 0.2(4x-1.5)-0.5(5x-0.8)=10(1.2-x). 　　总结升华：无论什么样的一元一次方程，其解题步骤概括无非就是“去分母，去括号， - 10 - 移项，合并，未知数系数化 1”这几个步骤，从操作步骤上来讲很容易掌握，但由于进行每 个步骤时都有些需注意的细节，许多都是我们认识问题的思维瑕点，需反复关注，并落实理 解记忆才能保证解方程问题――做的正确率.若仍不够自信，还可以用检验步骤予以辅助， 理解方程“解”的概念. 类型二：一元二次方程 　　 3．已知：3 是关于 x 的方程 的一个解，则 2a 的值是( ) 　　A.11 　　　B.12 　　　C.13　　　 D.14 　　解：只需将 x=3 代入方程，再解方程 12-2a+1=0，得到 ，所以 2a 为 13.故选 C. 　　总结升华：此题既考察了方程解的概念，又考查了方程的解法，这种用方程解的概念求 待定系数的题目是较为常见的. 　　举一反三： 　　【变式 1】已知 x=-1 是关于 x 的方程 的一个根，则 a=________. 　　解：把 x=-1 代入原方程，得 ，即 a2+a-2=0 　　　　所以 ，解得 a1=1，a2=-2. 　　答案：1 或-2. 　　总结升华：方程的解一定适合原方程，把这个解代入原方程求出 a 的值. 　　【变式 2】已知关于 x 的一元二次方程 x2-(k＋1)x-6=0 的一个根是 2，求方程的另一根 和 k 的值. 　　解：把 x=2 代入方程，得 4-2k-2-6=0 　　　　∴k=-2. 　　　　∴原方程为 x2+x-6=0 　　　　解之得：x1=2，x2=-3 　　　　所以方程的另一根为-3，k 值为-2. - 11 - 　　 4．按要求解一元二次方程. 　　(1)x2+4x+4=1(直接开平方法) 　　思路点拨：很清楚，x2+4x+4 是一个完全平方式，那么原方程就转化为(x+2)2=1． 　　解：由已知，得：(x+2)2=1 　　　　直接开平方，得：x+2=±1 　　　　即 x+2=1，x+2=-1 　　　　所以，方程的两根 x1=-1，x2=-3.　 　　(2)6x2-7x+1=0(配方法) 　　解：移项，得：6x2-7x=-1 　　　　二次项系数化为 1，得：x2- x=- 　　　　配方，得：x2- x+( )2=- +( )2 　　　　(x- )2= 　　　　x- =± 　　　　x1= + = =1；x2=- + = = . 　　(3)5x+2=3x2(公式法) 　　思路点拨：用公式法解一元二次方程，首先应把它化为一般形式，然后代入公式即 可． 　　解：将方程化为一般形式 　　　　3x2-5x-2=0 　　　　a=3，b=-5，c=-2 　　　　b2-4ac=(-5)2-4×3×(-2)=49＞0 　　　　x= - 12 - 　　　　所以 x1=2，x2=- . 　　(4)(x-2)2=2x-4(因式分解法) 　　思路点拨：等号右侧移项到左侧得-2x+4 提取-2 因式，即-2(x-2)，再提取公因式 x-2， 便可达到分解因式；一边为两个一次式的乘积，另一边为 0 的形式 　　解：移项，得(x-2)2-2x+4=0 　　　　(x-2)2-2(x-2)=0 　　　　因式分解，得：(x-2)(x-2-2)=0 　　　　整理，得：(x-2)(x-4)=0 　　　　于是，得 x-2=0 或 x-4=0 　　　　x1=2，x2=4. 　　 5．关于 x 的方程 x2 -kx+k-2=0 的根的情况是( ) 　　A.有两个不相等的实数根　　　　 B.有两个相等的实数根 　　C.无实数根　　　　　　　　　　 D.不能确定 　　考点：一元二次方程根的判别式. 　　思路点拨：对于一元二次方程而言，当判别式△＞0 时方程有二个不相等实数根，当△＜ 0 时方程无实数根，当△=0 时方程有二个相等实数根，所以判定一元二次方程根的情况关键 是求“△”. 　　解：△=k2-4(k-2)=k2-4k+8=(k-2)2+4，所以无论 k 取任何数，△总是大于 0 的， 　　　　所以该方程有两个不相等实数根.应选 A. 　　举一反三： 　　【变式 1】若关于 x 的一元二次方程(a-2)x2-2ax+a+1=0 没有实数解，求 ax+3＞0 的解 集(用含 a 的式子表示)． 　　思路点拨：要求 ax+3＞0 的解集，就是求 ax＞-3 的解集，那么就转化为要判定 a 的值 是正、负或 0．因为一元二次方程(a-2)x2-2ax+a+1=0 没有实数根，即(-2a)2-4(a-2)(a+1)＜ 0 就可求出 a 的取值范围． 　　解：∵关于 x 的一元二次方程(a-2)x2-2ax+a+1=0 没有实数根． - 13 - 　　　　∴(-2a)2-4(a-2)(a+1)=4a2-4a2+4a+8＜0 　　　　a＜-2 　　　　∵ax+3＞0 即 ax＞-3 　　　　∴x＜- 　　　　∴所求不等式的解集为 x＜- . 类型三：二元一次方程组 　　 6．已知方程 是一个二元一次方程，求 m 和 n 的值. 　　思路点拨：二元一次方程必须是同时符合下列两个条件的整式方程：①方程中含有两个 未知数；②方程中含有未知数的项的次数都是 1. 　　解：由题意得：m+3=1，1-2n=1. 　　　　∴m=-2，n=0. 　　举一反三： 　　【变式 1】下列方程组中，是二元一次方程组的有哪些？ 　 　 (1) 　 (2) 　 (3) 　 (4) 　 (5) 　　思路点拨：由二元一次方程组的定义可知：①方程组中的每个方程必须都是一次方程；② 方程组中的未知数共有两个；③方程组中的两个方程必须都为整式方程. 　　解：方程组(1)中含有 3 个未知数；(2)中的 xy=2 是二元二次方程；(5)中的 +y=6 不 是整式方程. 　　　　所以(3)，(4)是二元一次方程组. - 14 - 　　 7．方程组 的解为(　　). 　　(A) 　　　　(B) 　　　　(C) 　　　　(D)以上答案均不对 　　思路点拨：未知数 x、y 的一对值必须同时满足已知方程组的每个方程，才是方程组的 解. 　　解：把 x=-2，y=2 代入方程①， 　　　　左边=3×(-2)+4×2=2=右边， 　　　　再代入方程②， 　　　　左边=2×(-2)-2=-6，右边=5. 　　　　∵左边≠右边. 　　　　∴(A)满足方程①但不满足方程②，故不是原方程组的解. 　　　　同理可得，(B)满足方程①又满足方程②，所以是原方程组的解； 　　　　而(C)满足方程②但不满足方程①，故不是方程组的解.∴答案选择 B. 　　举一反三： 　　【变式 1】已知 是方程 3x-ay-2a=3 的一个解，求 a 的值. 　　思路点拨：由 是方程 3x-ay-2a=3 的一个解，可以理解为 x，y 的值适合方程 3x-ay-2a=3，也就是说方程 3x-ay-2a=3 中的 x 取-2，y 取 时方程成立.这样就可以将 x=-2， y= 代入方程中，转化为关于 a 的一元一次方程，可求出 a 值. 　　解：∵ x=-2， y= 是方程 3x-ay-2a=3 的一个解， - 15 - 　　　　∴ 3(-2)-a( )-2a=3 　　　　∴ -6- -2a=3， ∴- a=9， ∴a=- . 　　【变式 2】(烟台)写出一个解为 的二元一次方程组________________. 　　思路点拨：此题为开放性试题，由二元一次方程组的解的定义，需同时满足每个方程， 答案不唯一. 　　解： 或 等等. 　　 8．解方程组. 　　(1) 　　思路点拨：用代入法解二元一次方程组时，要尽量选取一个未知数的系数的绝对值是 1 的方程去变形，此例中②式 y 的系数为-1，所以用含 x 的代数式表示 y，代入①中消去 y. 　　解：由②得 y=5x-3 ③ 　　　　把③代入①得 2x+3(5x-3)=-9， 　　　　17x=0， x=0. 　　　　把 x=0 代入③得 y=-3. 　　　　∴ 　　(2) 　　思路点拨：此方程组的两个方程中 y 的系数互为相反数，所以可把两个方程相加，消去 y，解出 x 的值；又发现两个方程中 x 的系数相等，所以可把两个方程相减，消去 x，解出 y 的值. - 16 - 　　解法一：①+②，得 6x=18，∴ x=3. 　　　　　　把 x=3 代入②，得 9-2y=5，∴ y=2. 　　　　　　∴ 　　解法二：①-②，得 4y=8，∴ y=2. 　　　　　　把 y=2 代入②，得 3x-2×2=5，∴ x=3. 　　　　　　∴ 　　(3) 　　思路点拨：此方程组中两个未知数的系数均不成整数倍，所以选择系数较简单的未知数 消元.将①×4， ②×3，使得 x 的系数相等，再相减消去 x. 　　解：①×4，得 12x+20y=100......③ 　　　　②×3 得 12x+9y=45.....④ 　　　　③-④，得 11y=55.∴ y=5. 　　　　把 y=5 代入②，得 4x+3×5=15，∴ x=0. 　　　　∴ 　　举一反三： 　　【变式 1】解方程组. 　　(1) 　　分析：这两个方程都需要整理成标准形式，这样有利于确定消去哪个未知数. 　　解：整理原方程组，得 　　　　 　　　　由④得，y=3x-4. ⑤ - 17 - 　　　　把⑤代入③，得 3x-2(3x-4)=2， 　　　　x=2. 　　　　把 x=2 代入⑤，得 y=3×2-4=2， 　　　　∴ 　　(2) 　　分析：此方程组中没有一个未知数的系数的绝对值是 1，所以考虑用加减消元法，选择 消去系数较简单的未知数 x，由①和②，①和③两次消元，得到关于 y，z 的二元一次方程 组，最后求 x. 　　解：①×3，得 6x+18y+9z=18......④ 　　　　②×2，得 6x+30y+14z=12......⑤ 　　　　⑤-④，得　12y+5z=-6.....⑥ 　　　　①×2，得 4x+12y+6z=12.......⑦ 　　　　⑦-③， 得 21y+2z=3......⑧ 　　　　由⑥和⑧组成方程组 　　　　解这个方程组，得 　　　　把 y= ， z=-2 代入①，得 2x+6× +3×(-2)=6， 　　　　∴ x=5. 　　　　∴ 类型四：分式方程 - 18 - 　　 9．下列方程中哪个是关于 x 的分式方程？ 　 　 A. 　 　 　 B. 　 　 　 C. 　 　 　 D. 　　思路点拨：根据分式方程的定义. 　　解：A 为整式方程；B 中虽含有分母，但分母中不含未知数 x；C 中含有分式，但分母中 不含未知数 x；根据定义，只有 D 是关于 x 的分式方程． 　　 10．解分式方程. 　　(1) 　　思路点拨：方程 是一个分式方程，根据方程的同解原理，可以把它化为一 个一元一次方程，两边同时乘以 x+1，得 3x-4=2(x+1)，但方程的同解原理要求，x+1≠0，∴ 解完方程以后要验根. 　　解：3x-4=2(x+1)，3x-4=2x+2 　　　　∴x=6， 　　　　检验：当 x=6 时，x+1=7≠0， 　　　　∴x=6 是原方程的解. 　　(2) 　　思路点拨：去分母时注意方程中每一项都要乘以各分母的最小公倍数，等号右边的数字 3 不要漏乘；还要注意验根. 　　解：去分母得， 　　　　 　　　　经检验，x=2 不是原方程的解， - 19 - 　　　　 原方程无解． 　　 11．已知方程 无解，求 m 的值． 　　思路点拨：此分式方程无解，说明去分母后得到的 x 的值使得分式无意义，即最简公分 母为 0． 　　解： 　　　　去分母得， 　　　　 　　　　 原方程无解， 或 　　　　当 时， ； 　　　　当 时， ． 　　　　 的值为 8 或 20． 　　举一反三： 　　【变式 1】关于 x 的方程 的解是非负数，求 a 与 b 的关系． 　　思路点拨：先求出方程的解，再令 ． 　　解：去分母得， 　　　　 　　　　 此分式方程的解是非负数， 　　　　 ． - 20 - 　　【变式 2】如果 ，试求 A、B 的值． 　　解法 1：(利用分式的加减法) 　　　　　 　　　　　 　　　　　 　　解法 2：去分母得， 　　　　　 　　　　　 类型五：方程及方程组的应用 　　 12．近年来，由于受国际石油市场的影响，汽油价格不断上涨，请你根据下面的 信息，帮小明计算今年 5 月份每升汽油的价格. 　　　　　　 - 21 - 　　解：设去年 5 月份汽油价格为 元/升，则今年 5 月份的汽油价格为 元/升， 　　　　根据题意，得 　　　　整理，得 . 　　　　解这个方程，得 . 　　　　经检验， 是原方程的解. 　　　　所以 . 　　答：今年 5 月份的汽油价格为 元/升. 　　 13．(上海市)2001 年以来，我国曾五次实施药品降价，累计降价的总金额为 269 亿元，五次药品降价的年份与相应降价金额如表所示，表中缺失了 2003 年、2007 年相关数 据.已知 2007 年药品降价金额是 2003 年药品降价金额的 6 倍，结合表中信息，求 2003 年和 2007 年的药品降价金额. 年份 2001 2003 2004 2005 2007 降价金额(亿元) 54 　 35 40 　 - 22 - 　　解：[解法一]设 2003 年和 2007 年的药品降价金额分别为 x 亿元、y 亿元. 　　　　　　　　根据题意，得 　　　　　　　　解方程组，得 　　　　　　　　答：2003 年和 2007 年的药品降价金额分别为 20 亿元和 120 亿元. 　　　　[解法二]设 2003 年的药品降价金额为 x 亿元， 　　　　　　　　则 2007 年的药品降价金额为 6x 亿元. 　　　　　　　　根据题意，得 54+x+35+40+6x=269. 　　　　　　　　解方程，得 x=20，所以 6x=120. 　　　　　　　　答：2003 年和 2007 年的药品降价金额分别为 20 亿元和 120 亿元. 　　 14．(浙江宁波)2007 年 5 月 19 日起，中国人民银行上调存款利率. 　　　　　　　　　　　　　　　　　　　人民币存款利率调整表 项 目 调整前年利率% 调整后年利率% 活期存款 0.72 0.72 一年期定期存款 2.79 3.06 储户的实得利息收益是扣除利息税后的所得利息，利息税率为 20%. 　　(1)小明于 2007 年 5 月 19 日把 3500 元的压岁钱按一年期定期存入银行，到期时他实得 利息收益是多少元? 　　(2)小明在这次利率调整前有一笔一年期定期存款，到期时按调整前的年利率 2.79%计 息，本金与实得利 　 　　息收益的和为 2555.8 元，问他这笔存款的本金是多少元? 　　(3)小明爸爸有一张在 2007 年 5 月 19 日前存人的 10000 元的一年期定期存款单，为获 取更大的利息收益， 　 　　想把这笔存款转存为利率调整后的一年期定期存款.问他是否应该转存?请说明理由. 　　约定： 　　①存款天数按整数天计算，一年按 360 天计算利息. 　　②比较利息大小是指从首次存入日开始的一年时间内.获得的利息比较.如果不转存，利 - 23 - 息按调整前的一年期定期利率计算；如果转存，转存前已存天数的利息按活期利率计算，转 存后，余下天数的利息按调整后的一年期定期利率计算(转存前后本金不变). 　　解：(1)3500×3.06%×80%=85.68(元)， 　　　　　 ∴到期时他实得利息收益是 85.68 元. 　　　　(2)设他这笔存款的本金是 x 元， 　 　　　　则 x(1+2.79%×80%)=2555.8， 　 　　　　解得 x=2500， 　 　　　　∴这笔存款的本金是 2500 元. 　　　　(3)设小明爸爸的这笔存款转存前已存了 x 天，由题意得 　 　　　　 　 　　　　解得 　 　　　　当他这笔存款转存前已存天数不超过 41 天时，他应该转存；否则不需转存. 中考题萃 一、选择题： 　　1.(浙江丽水)方程组 ，由②-①，得正确的方程是( ) 　　A.3x=10 　　　B.x=5　　　 C.3x=-5 　　　D.x=-5 　　2.(湖南株州)二元一次方程组 的解是( ) 　　A. 　　　B. 　　　 C. 　　　D. 　 　 3.( 山 东 淄 博 ) 若 方 程 组 的 解 是 则 方 程 组 的解是( ) - 24 - 　　A. 　　　B. 　　　C. 　　　D. 　　4.(四川达州)某商品原价 100 元，连续两次涨价 x%后售价为 120 元，下面所列方程正 确的是( ) 　　A.100(1-x%)2=120 　　　　B.100(1+x%)2=120 　　C.100(1+2x%)=120 　　　　D.100(1+x2%)=120 　　5.(湖北宜宾)某班共有学生 49 人.一天，该班某男生因事请假，当天的男生人数恰为女 生人数的一半.若 　　　设该班男生人数为 x，女生人数为 y，则下列方程组中，能正确计算出 x、y 的是( ) 　 　 A ． 　 　 　 B. 　 　 　 C. 　 　 　 D. 　　6.一副三角扳按如图方式摆放，且∠1 的度数比∠2 的度数大 50°，若设∠1=x°，∠2=y °，则可得到方 　　　程组为( ) 　　　　　　　　　　　　　　　　　　　　　　　 　 　 A. 　 　 　 B. 　 　 　 C. 　 　 　 D. 　　7.(河北省)炎炎夏日，甲安装队为 A 小区安装 66 台空调，乙安装队为 B 小区安装 60 台 空调，两队同时开工 - 25 - 　　　且恰好同时完工，甲队比乙队每天多安装 2 台．设乙队每天安装 x 台，根据题意，下 面所列方程中正确 　　　的是( ) 　　A． 　　　B． 　　　C． 　　　D． 　 　 8.( 山 东 ) 若 方 程 组 的 解 是 ， 则 方 程 组 的解是( ) 　　A. 　　　B. 　　　C. 　　　D. 　　9.(成都市)下列关于 的一元二次方程中，有两个不相等的实数根的方程是( ) 　 　 A ． 　 　 　 B ． 　 　 　 C ． 　　　 D． 　　10.(黑龙江伊春)为了奖励进步较大的学生，某班决定购买甲、乙、丙三种钢笔作为奖 品，其单价分别 　 　　为 4 元、5 元、6 元，购买这些钢笔需要花 60 元；经过协商，每种钢笔单价下降 l 元，结果只花了 48 　 　　元，那么甲种钢笔可能购买( ) 　　A.11 支 　　　B.9 支　　　 C.7 支 　　　D.5 支 二、填空题： 　　11.(四川宜宾)若方程组 的解是 ，那么 ________． 　　12.(广东省)已知 a、b 互为相反数，并且 3a-2b=5，则 a2＋b2=________. - 26 - 　　13.(北京)若分式 的值为 0，则 的值为____________. 　　14.(北京)若关于 x 的一元二次方程 没有实数根，则 k 的取值范围是 ____________. 　　15.(上海市)若方程 的两个实数根为 ， ，则 ____________． 三、解答题： 　　16.解方程： 　　17.(成都市)解方程： ． 　　18.(山东)解方程： . 　　19.(北京)解方程： . 　　20.(上海市)解方程： ． 　　21.(旅顺)已知关于 x 的方程 的一个解与方程 的解相同． 　　⑴求 k 的值； 　　⑵求方程 的另一个解. 　　22.(安徽省)据报道，我省农作物秸杆的资源巨大，但合理利用量十分有限，2006 年的 利用率只有 30%，大部分秸杆被直接焚烧了，假定我省每年产出的农作物秸杆总量不变，且 - 27 - 合理利用量的增长率相同，要使 2008 年的利用率提高到 60%，求每年的增长率.(取 ≈ 1.41) 　　23.(广东省)某文具厂加工一种学生画图工具 2500 套，在加工了 1000 套后，采用了新 技术，使每天的工作效率是原来的 1.5 倍，结果提前 5 天完成任务，求该文具厂原来每天加 工多少套这种学生画图工具. 　　24.(长沙)在社会主义新农村建设中，某乡镇决定对一段公路进行改造．已知这项工程 由甲工程队单独做需要 40 天完成；如果由乙工程队先单独做 10 天，那么剩下的工程还需要 两队合做 20 天才能完成． 　　(1)求乙工程队单独完成这项工程所需的天数； 　　(2)求两队合做完成这项工程所需的天数． 　　25.（南宁市）小李骑自行车从 A 地到 B 地，小明骑自行车从 B 地到 A 地，两人都匀速 前进.已知两人在上午 8 时同时出发，到上午 10 时，两人还相距 36 千米，到中午 12 时，两 人又相距 36 千米.求 A、B 两地间的路程. 　 　　　　　　　　　　　　　 　　26.(东莞市)在 2008 年春运期间，我国南方出现大范围冰雪灾害，导致某地电路断 电．该地供电局组织电工进行抢修．供电局距离抢修工地 15 千米．抢修车装载着所需材料 先从供电局出发，15 分钟后，电工乘吉普车从同一地点出发，结果两车同时到达抢修工 地．已知吉普车速度是抢修车速度的 1.5 倍，求这两种车的速度． 　　27.(沈阳)某工程队再我市实施棚户区改造过程中承包了一项拆迁工程.原计划每天拆 迁 1250m2，因为准备工作不足，第一天少拆迁了 20％.从第二天开始，该工程队加快了拆迁 速度，第三天拆迁了 1440m2.求：(1)该工程队第一天拆迁的面积；(2)若该工程队第二天、 - 28 - 第三天每天的拆迁面积比前一天增加的百分数相同，求这个百分数. 　　28.(海南)在“五一”黄金周期间，小明、小亮等同学随家长一同到热带海洋世界游玩， 下面是购买门票时，小明与他爸爸的对话(如图)，试根据图中的信息，解答下列问题. 　　(1)小明他们一共去了几个成人，几个学生? 　　(2)请你帮助小明算一算，用哪种方式购票更省钱?说明理由． 　　　　　　　　　　　　　 答案与解析： 一、选择题 　　1. B 2. A 3. A 4.B 5. D 6. D 7. D 8. C 9. D 10.D 二、填空题 　　11. 1 12. 2 13. 2 14. 15.2 三、解答题 　　16.解：去分母，得 　　　　　 去括号，得 　　　　　 移项合并，得 　　　　　 系数化为 1，得 x=2. 　　　　　 经检验 x=2 是原方程的根. - 29 - 　　　　　 ∴ 原方程的根为 x=2. 　　17.解：去分母，得 ． 　　　　　 去括号，得 ． 　　　　　 解得 ． 　　　　　 经检验 是原方程的解． 　　　　　 原方程的解是 ． 　　18.解：两边同乘以(x+1)(1-2x)，得(x-1)(1-2x)+2x(x+1)=0 　　　　　 整理，得 5x-1=0 　　　　　 解得 　　　　　 经检验， 是原方程的根. 　　19.解：因为 a=1，b=4，c=-1， 　　　　　 所以 . 　　　　　 代入公式，得 . 　　　　　 所以原方程的解为 . 　　20.解：去分母，得 ， 　　　　　 整理，得 ， 　　　　　 解方程，得 ． 　　　　　 经检验， 是增根， 是原方程的根， 原方程的根是 ． - 30 - 　　21.解：(1)∵ 　　　　　 　 ∴ 　　　　　 　 ∴ 　　　　　 　 经检验 是原方程的解 　　　　　 　 把 代入方程 　　　　　 　 解得 k=3. 　　　　　 (2)解 ，得 　　　　　 　 ，x2=1 　　　　　 　 ∴方程 的另一个解为 x=1 　　22.解：设我省每年产出的农作物秸杆总量为 a，合理利用量的增长率是 x，由题意得： 　　　　　 a·30%·(1＋x)2=a·60%，即(1＋x)2=2 　　　　　 ∴x1≈0.41，x2≈-2.41(不合题意舍去). 　　　　　 ∴x≈0.41. 　　　　　 即我省每年秸秆合理利用量的增长率约为 41%. 　　23.解：设该文具厂原来每天加工 x 套画图工具， 　　　　　 依题意有 　　　　　 解方程得 x=100 　　　　　 经检验 x=100 是原方程的根 　　　　　 答：该文具厂原来每天加工 100 套画图工具. - 31 - 　　24.(1)解：设乙工程队单独完成这项工程需要 天，根据题意得： 　　　　　　　 　　　　　　　解之得： 经检验： 是原方程的解． 　　　　　　　答：乙工程队单独完成这项工程所需的天数为 60 天． 　　　 (2)解：设两队合做完成这项工程所需的天数为 天，根据题意得： 　　　　　　　 　　　　　　　解之得： 　　　　　　　答：两队合做完成这项工程所需的天数为 24 天． 　　25.解：设 A、B 两地间的路程为 x 千米，根据题意，得 　　　　　 　　　　　 解得 　　　　　 答：A、B 两地间的路程为 108 千米. 　　26.解：设抢修车的速度为 千米/时，则吉普车的速度为 千米/时 由题意得 　　　　　 　　　　　 解得 　　　　　 经检验： 是原方程的解 　　　　　 ∴当 x=20 时， 1.5x=30 　　　　　 答：抢修车的的速度为 20 千米/时，吉普车的速度为 30 千米/时. 　　27.解：(1)1250(1-20%)=1000(m2) 　　　　　 　 所以，该工程队第一天拆迁的面积为 1000m2； 　　　　　 (2)设该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数是 x 　　　　　 　 则 1000(1+x)2=1440 - 32 - 　　　　　 　 解得 x1=0.2=20%，x2=-2.2(舍) 　　　　　 　 所以，该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数是 20%. 　　28.解：(1)设小明他们一共去了 x 个成人，则去了学生(12-x)人，依题意，得 　　　　　 　 35x+0.5×35(12-x)=350 x=8 　　　　　 　 答：小明他们一共去了 8 个成人，去了学生 4 人． 　　　　　 (2)若按 16 个游客购买团体票，需付门票款为 35×0.6×16=336(元) 　　　　　 　 ∵ 336＜350 ∴ 按 16 人的团体购票更省钱．