海南2103年中考数学卷 10页

‎2013年中考数学试题（海南省卷）‎ ‎（本试卷满分120分，考试时间100分钟）‎ 一、选择题（共14小题，每小题3分，满分42分）在下列各题的选项中，有且只有一个是正确的。‎ ‎1．（2013年海南省3分）﹣5的绝对值是【 】‎ A． B． C． D．‎ ‎【答案】C ‎2．（2013年海南省3分）若代数式x+3的值为2，则x等于【 】‎ A． B． C． D．‎ ‎【答案】B。‎ ‎3．（2013年海南省3分）下列计算正确的是【 】‎ A． B． C． D．‎ ‎【答案】D。‎ ‎4．（2013年海南省3分）某班5位学生参加中考体育测试的成绩（单位：分）分别是35、40、37、38、40．则这组数据的众数是【 】‎ A．37 B．‎40 C．38 D．35‎ ‎【答案】B。‎ ‎5．（2013年海南省3分）如图是由5个大小相同的正方体组成的几何体，它的俯视图为【 】‎ ‎ A． B． C． D．‎ ‎【答案】A。‎ ‎6．（2013年海南省3分）下列各数中，与的积为有理数的是【 】‎ A． B． C． D．‎ ‎【答案】C。‎ ‎7．（2013年海南省3分）“辽宁号”航母是中国海军航空母舰的首舰，标准排水量57000吨，满载排水量67500吨，数据67500用科学记数法表示为【 】‎ A．675×102 B．67.5×‎102 C．6.75×104 D．6.75×105‎ ‎【答案】C。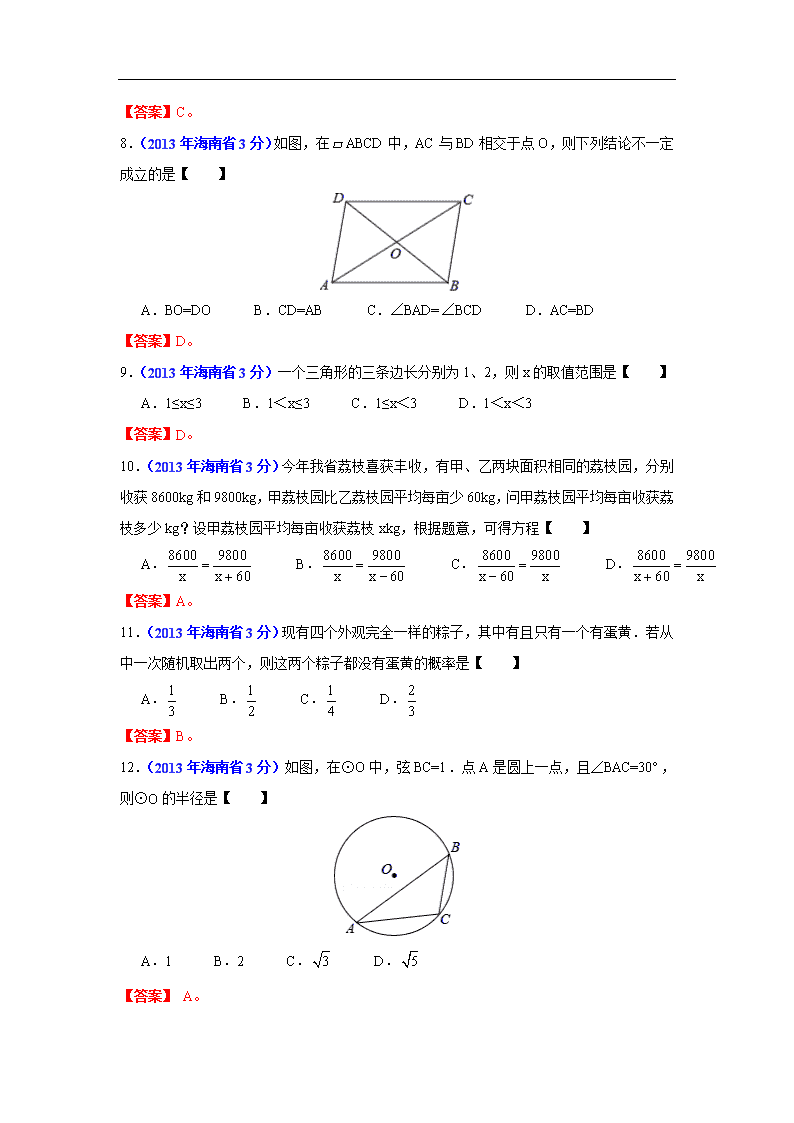‎ ‎8．（2013年海南省3分）如图，在ABCD中，AC与BD相交于点O，则下列结论不一定成立的是【 】‎ A．BO=DO B．CD=AB C．∠BAD=∠BCD D．AC=BD ‎【答案】D。‎ ‎9．（2013年海南省3分）一个三角形的三条边长分别为1、2，则x的取值范围是【 】‎ A．1≤x≤3 B．1＜x≤‎3 C．1≤x＜3 D．1＜x＜3‎ ‎【答案】D。‎ ‎10．（2013年海南省3分）今年我省荔枝喜获丰收，有甲、乙两块面积相同的荔枝园，分别收获‎8600kg和‎9800kg，甲荔枝园比乙荔枝园平均每亩少‎60kg，问甲荔枝园平均每亩收获荔枝多少kg？设甲荔枝园平均每亩收获荔枝xkg，根据题意，可得方程【 】‎ A． B． C． D．‎ ‎【答案】A。‎ ‎11．（2013年海南省3分）现有四个外观完全一样的粽子，其中有且只有一个有蛋黄．若从中一次随机取出两个，则这两个粽子都没有蛋黄的概率是【 】‎ A． B． C． D．‎ ‎【答案】B。‎ ‎12．（2013年海南省3分）如图，在⊙O中，弦BC=1．点A是圆上一点，且∠BAC=30°，则⊙O的半径是【 】‎ A．1 B．‎2 C． D．‎ ‎【答案】 A。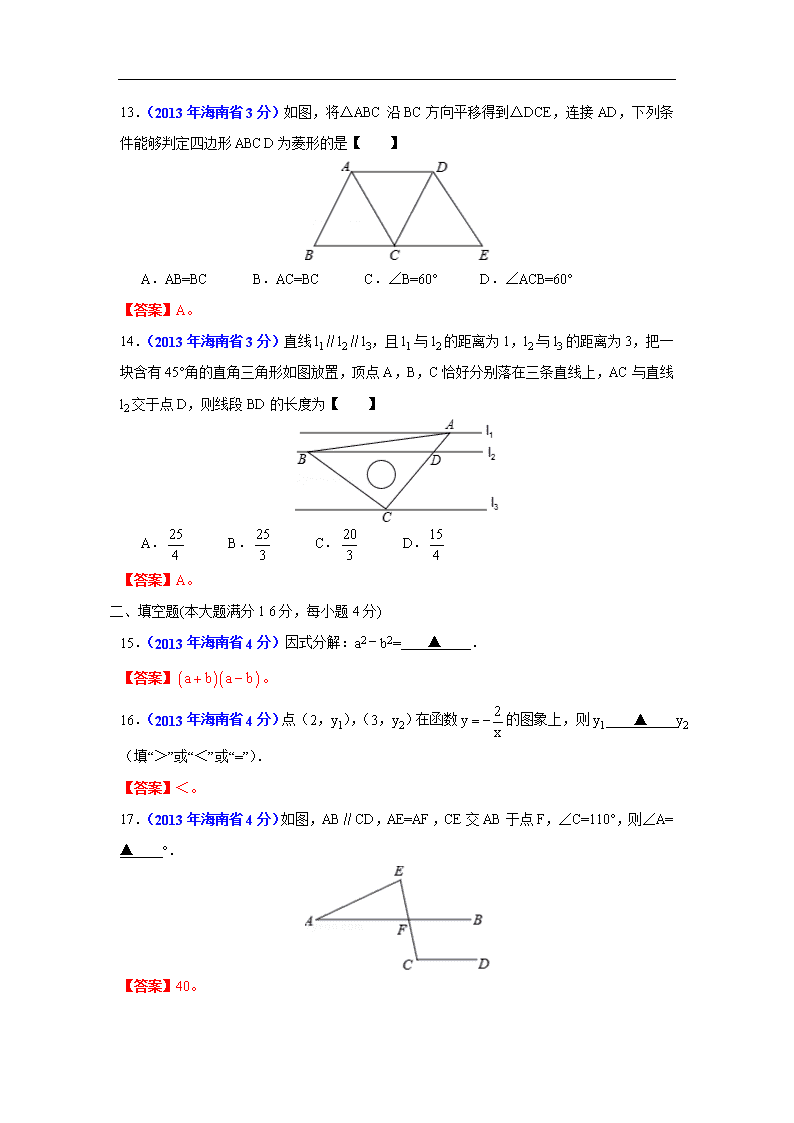‎ ‎13．（2013年海南省3分）如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件能够判定四边形ABCD为菱形的是【 】‎ A．AB=BC B．AC=BC C．∠B=60° D．∠ACB=60°‎ ‎【答案】A。‎ ‎14．（2013年海南省3分）直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3，把一块含有45°角的直角三角形如图放置，顶点A，B，C恰好分别落在三条直线上，AC与直线l2交于点D，则线段BD的长度为【 】‎ A． B． C． D．‎ ‎【答案】A。‎ 二、填空题(本大题满分1 6分，每小题4分)‎ ‎15．（2013年海南省4分）因式分解：a2﹣b2=　 ▲ 　．‎ ‎【答案】。‎ ‎16．（2013年海南省4分）点（2，y1），（3，y2）在函数的图象上，则y1　 ▲ 　y2（填“＞”或“＜”或“=”）．‎ ‎【答案】＜。‎ ‎17．（2013年海南省4分）如图，AB∥CD，AE=AF，CE交AB于点F，∠C=110°，则∠A=　 ▲ 　°．‎ ‎【答案】40。‎ ‎18．（2013年海南省4分）如图，在梯形ABCD中，AD∥BC，AB=CD=AD=5，∠B=60°，则BC=　 ▲ 　．‎ ‎【答案】10。‎ 三、解答题（共6小题，满分62分）‎ ‎19．（2013年海南省10分）计算：‎ ‎（1）（2013年海南省5分）计算：； ‎ ‎【答案】解：原式=。‎ ‎（2）（2013年海南省5分）计算：．‎ ‎【答案】解：原式=。‎ ‎20．（2013年海南省8分）据悉，2013年财政部核定海南省发行的60亿地方政府“债券资金”，全部用于交通等重大项目建设．以下是60亿“债券资金”分配统计图：‎ ‎（1）请将条形统计图补充完整；‎ ‎（2）在扇形统计图中，a=　 ▲ 　，b=　 ▲ 　（都精确到0.1）；‎ ‎（3）在扇形统计图中，“教育文化”对应的扇形圆心角的度数为　 ▲ 　°（精确到°1）‎ ‎【答案】解：（1）城乡“债券资金”为：60﹣22﹣10.7﹣6.3﹣3.3﹣5.4=12.3，将条形统计图补充完整如下：‎ ‎（2）36.7；20.5。‎ ‎（3）64．‎ ‎21．（2013年海南省9分）如图，在正方形网格中，△ABC各顶点都在格点上，点A，C的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：‎ ‎（1）画出△ABC关于y轴对称的△A1B‎1C1；‎ ‎（2）画出△ABC关于原点O对称的△A2B‎2C2；‎ ‎（3）点C1的坐标是　 ▲ 　；点C2的坐标是　 ▲ 　；过C、C1、C2三点的圆的圆弧的长是 ‎　 ▲ 　（保留π）．‎ ‎【答案】解：（1）△A1B‎1C1如图所示。‎ ‎ （2）△A2B‎2C2如图所示。‎ ‎（3）（1，4）；（1，﹣4）；。‎ ‎22．（2013年海南省8分）为迎接‎6月5日的“世界环境日”，某校团委开展“光盘行动”，倡议学生遏制浪费粮食行为．该校七年级（1）、（2）、（3）三个班共128人参加了活动．其中七（3）班48人参加，七（1）班参加的人数比七（2）班多10人，请问七（1）班和七（2）班各有多少人参加“光盘行动”？‎ ‎【答案】解：设七（2）班有x人参加“光盘行动”，则七（1）班有（x+10）人参加“光盘行动”，依题意有 ‎（x+10）+x+48=128，‎ 解得x=35，‎ 则x+10=45。‎ 答：七（1）班有45人参加“光盘行动”，七（2）班有35人参加“光盘行动”。‎ ‎23．（2013年海南省13分）（1）如图（1）点P是正方形ABCD的边CD上一点（点P与点C，D不重合），点E在BC的延长线上，且CE=CP，连接BP，DE．求证：△BCP≌△DCE；‎ ‎（2）直线EP交AD于F，连接BF，FC．点G是FC与BP的交点．‎ ‎①若CD=2PC时，求证：BP⊥CF；‎ ‎②若CD=n•PC（n是大于1的实数）时，记△BPF的面积为S1，△DPE的面积为S2．求证：S1=（n+1）S2．‎ ‎【答案】证明：（1）∵在△BCP与△DCE中，，‎ ‎∴△BCP≌△DCE（SAS）。‎ ‎（2）①∵CP=CE，∠PCE=90°，∴∠CPE=45°。∴∠FPD=∠CPE=45°。∴∠PFD=45°。∴FD=DP。‎ ‎∵CD=2PC，∴DP=CP。∴FD=CP。‎ ‎∵在△BCP与△CDF中，，‎ ‎∴△BCP≌△CDF（SAS）。‎ ‎∴∠FCD=∠CBP。‎ ‎∵∠CBP+∠BPC=90°，∴∠FCD+∠BPC=90°。‎ ‎∴∠PGC=90°，即BP⊥CF。‎ ‎②设CP=CE=1，则BC=CD=n，DP=CD﹣CP=n﹣1，‎ 易知△FDP为等腰直角三角形，∴FD=DP=n﹣1。‎ ‎，‎ ‎，‎ ‎∴S1=（n+1）S2。‎ ‎24．（2013年海南省14分）如图，二次函数的图象与x轴相交于点A（﹣3，0）、B（﹣1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y=kx﹣4k（k≠0）的图象过点P交x轴于点Q．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）当点P的坐标为（﹣4，m）时，求证：∠OPC=∠AQC；‎ ‎（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．连接AN，当△AMN的面积最大时，‎ ‎①求t的值；‎ ‎②直线PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．‎ ‎【答案】解：（1）∵二次函数的图象与x轴相交于点A（﹣3，0）、B（﹣1，0），‎ ‎∴设二次函数的解析式为：y=a（x+3）（x+1）。‎ ‎∵二次函数的图象经过点C（0，3），∴3=a×3×1，解得a=1。‎ ‎∴二次函数的解析式为：y=（x+3）（x+1），即y =x2+4x+3。‎ ‎ （2）证明：在二次函数解析式y=x2+4x+3中，当x=﹣4时，y=3，∴P（﹣4，3）。‎ ‎∵P（﹣4，3），C（0，3），∴PC=4，PC∥x轴。‎ ‎∵一次函数y=kx﹣4k（k≠0）的图象交x轴于点Q，当y=0时，x=4，∴Q（4，0），OQ=4。‎ ‎∴PC=OQ。‎ 又∵PC∥x轴，∴四边形POQC是平行四边形。‎ ‎∴∠OPC=∠AQC。‎ ‎（3）①在Rt△COQ中，OC=3，OQ=4，由勾股定理得：CQ=5．‎ 如答图1所示，过点N作ND⊥x轴于点D，则ND∥OC，‎ ‎∴△QND∽△QCO。‎ ‎∴，即，‎ 解得：。‎ 设S=S△AMN，则：‎ ‎。‎ 又∵AQ=7，点M的速度是每秒3个单位长度，‎ ‎∴点M到达终点的时间为t=，‎ ‎∴（0＜t≤）。‎ ‎∵＜0，＜，且x＜时，y随x的增大而增大，‎ ‎∴当t=时，△AMN的面积最大。‎ ‎②假设直线PQ能够垂直平分线段MN，则有QM=QN，且PQ⊥MN，PQ平分∠AQC。‎ 由QM=QN，得：7﹣3t=5﹣t，解得t=1。‎ 此时点M与点O重合，如答图2所示，‎ 设PQ与OC交于点E，由（2）可知，四边形POQC是平行四边形，‎ ‎∴OE=CE。‎ ‎∵点E到CQ的距离小于CE，‎ ‎∴点E到CQ的距离小于OE。‎ 而OE⊥x轴，‎ ‎∴PQ不是∠AQC的平分线，这与假设矛盾。‎ ‎∴直线PQ不能垂直平分线段MN。‎