北京市朝阳区中考数学模拟试题及答案 15页

‎2010年北京市朝阳区中考数学模拟试题 ‎ 一、选择题（共8道小题，每小题4分，共32分）‎ ‎1．－3的立方是（ ）‎ A．－27 B．－‎9 ‎ C．9 D．27‎ A B O ‎(第3题 )‎ ‎2．据统计，2008中国某小商品城市场全年成交额约为348.4亿元.近似数348.4亿元的有效数字的个数是( ) ‎ A．6个 B． 5个 C．4个 D．11个 ‎3．正方形网格中，如图放置，则的值为（ ）‎ A． B．‎2 ‎‎ ‎‎ ‎C． D． ‎ ‎4．已知甲、乙两组数据的平均数分别是，，方差分别是，，比较这两组数据，下列说法正确的是（ ）‎ A．乙组数据的波动较小 B．乙组数据较好 C．甲组数据的极差较大 D．甲组数据较好 ‎ ‎5．某等腰三角形的两条边长分别为‎3cm和‎6cm，则它的周长为（ ）‎ A．‎9cm B．‎12cm C．‎15cm D．‎12cm或‎15cm ‎6．下列四个三角形，与左图中的三角形相似的是（ ）‎ ‎（第6题）‎ A．‎ B．‎ C．‎ D．‎ ‎7. 函数与函数的图象交于A、B两点，设点A的坐标为，则边长分别为、的矩形面积和周长分别为（ ）‎ A. 4，12 B. 4，‎6 C. 8，12 D. 8，6‎ ‎8.如图，在Rt△ABC 中，，D、E是斜边BC上两点，且∠DAE=45°，将△‎ 绕点顺时针旋转90后，得到△，连接，下列结论：‎ ‎①△≌△； ②△∽△；　　‎ ‎③； ④‎ 其中一定正确的是 ‎ A．②④　　　　　　 B．①③‎ C．②③　　　　　　　 D．①④　　‎ 二、填空题（共4道小题，每小题4分，共16分）‎ ‎9. 分解因式 ．‎ ‎10. 函数中，自变量的取值范围是 ．‎ ‎11. 一个口袋里有4个白球，5个红球，6个黄球，每个球除颜色外都相同，搅匀后随机从袋中摸出一个球，这个球是白球的概率是 ‎ ‎12. 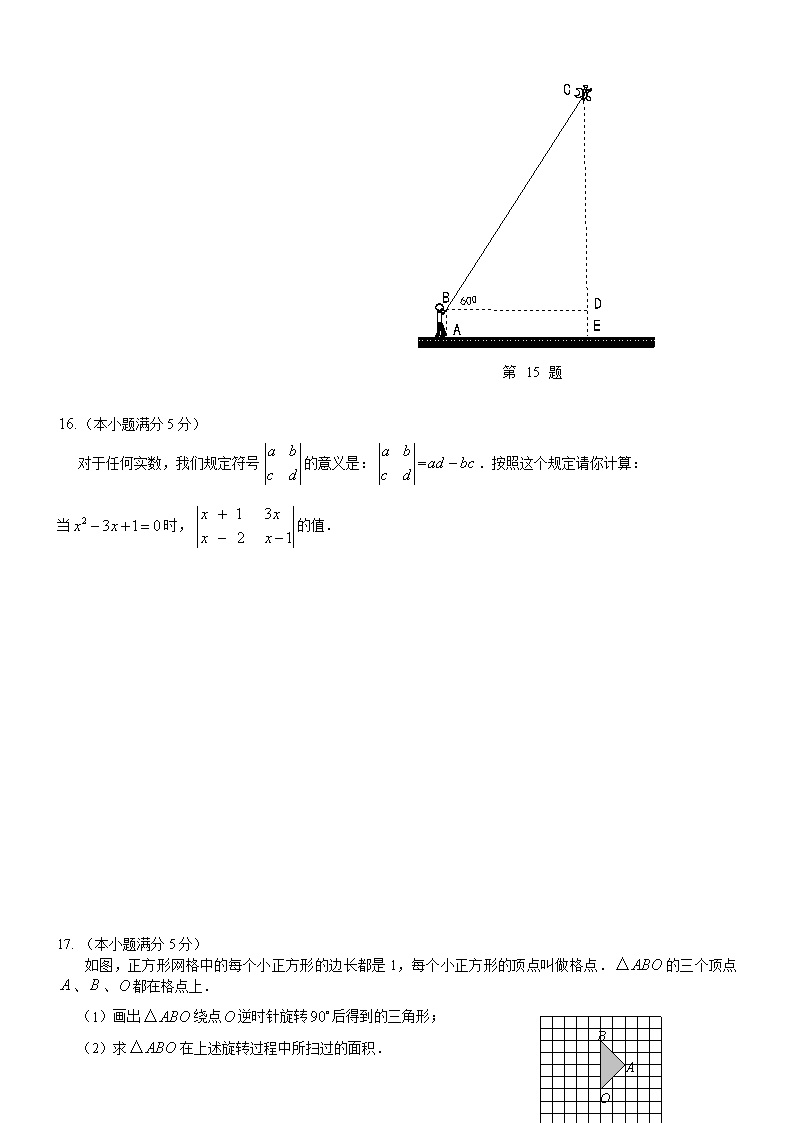如图，OA=OB，A点坐标是，OB与轴正方向夹角为，则B点坐标是 ．‎ ‎（第题图）‎ AB与轴交于点C，若以OC为轴，将沿OC翻折，B点落在第二象限内处，则的长度为 ．‎ ‎　　　　　　　　　　　　　　　　　　　　‎ 三、解答题（共13道小题，共 72 分）‎ ‎13．（本小题满分5分） 计算： .‎ ‎14．（本小题满分5分）解方程．‎ ‎15. （本小题满分5分）‎ 小明站在A处放风筝，风筝飞到C处时的线长为‎20米，这时测得∠CBD=60°，若牵引底端B离地面‎1.5米，求此时风筝离地面高度。(计算结果精确到‎0.1米，)‎ 第15题图 ‎（本小题满分5分）‎ 对于任何实数，我们规定符号的意义是：=．按照这个规定请你计算：‎ 当时， 的值．‎ ‎17. （本小题满分5分）‎ 如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．的三个顶点、、都在格点上．‎ ‎（第17题）‎ A B O ‎（1）画出绕点逆时针旋转后得到的三角形；‎ ‎（2）求在上述旋转过程中所扫过的面积．‎ ‎18．（本小题满分5分）‎ 如图，为半圆的直径，点C在半圆上，过点作的平行线交于点，交过点的直线于点，且.‎ ‎（1）求证：是半圆O的切线；‎ ‎（2）若，，求的长.‎ ‎19. （本小题满分5分）‎ 如图，在△ABC中，∠CAB、∠ABC的平分线交于点D，DE∥AC交BC于点E，DF∥BC交AC于点F．求证：四边形DECF为菱形．‎ ‎ ‎ ‎20．（本题满分5分）‎ 某校为了了解九年级学生体育测试成绩情况，以九年级（1）班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制成下两幅统计图（如图），请你结合图中所给信息解答下列问题：（说明：A级：90分—100分；B级：75分—89分；C级：60分—74分；D级：60分以下）‎ ‎（1）D级学生的人数占全班人数的百分比为 ；‎ ‎（2）扇形统计图中C级所在扇形圆心角度数为 ；‎ ‎（3）该班学生体育测试成绩的中位数落在等级 内；‎ ‎（4）若该校九年级学生共有500人，请你估计这次考试中A级和B级的学生共有多少人。‎ ‎25‎ ‎20‎ ‎15‎ ‎10‎ ‎5‎ ‎0‎ ‎13‎ ‎25‎ ‎10‎ ‎2‎ 人数 A B C D 等级 第20题图1‎ 第20题图2‎ ‎21．（本小题满分5分）‎ 一辆经营长途运输的货车在高速公路的处加满油后匀速行驶，下表记录的是货车一次加满油后油箱内余油量（升）与行驶时间（时）之间的关系：‎ 行驶时间（时）‎ ‎0‎ ‎1‎ ‎2‎ ‎2.5‎ 余油量（升）‎ ‎100‎ ‎80‎ ‎60‎ ‎50‎ ‎（1）请你认真分析上表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示与之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式；（不要求写出自变量的取值范围）‎ ‎（2）按照（1）中的变化规律，货车从处出发行驶4.2小时到达B处，求此时油箱内余油多少升？‎ ‎22．（本小题满分5分）‎ 定义为一次函数的特征数．‎ ‎（1）若特征数是的一次函数为正比例函数，求的值；‎ ‎（2）设点分别为抛物线与轴、轴的交点，其中，且的面积为4，为坐标原点，求图象过、两点的一次函数的特征数．‎ ‎23.（本题满分7分）‎ 已知二次函数的图象是C1．‎ ‎（1）求C1关于点R（1，0）中心对称的图象C2的函数解析式；‎ ‎（2）在（1）的条件下，设抛物线C1、C2与y轴的交点分别为A、B，当AB=18时，求的值．‎ ‎24.（本题满分7分）‎ ‎(1)已知：如图1，是⊙的内接正三角形，点为弧BC上一动点，求证：‎ ‎(2) 如图2，四边形是⊙的内接正方形，点为弧BC上一动点，求证: ‎ ‎(3) 如图3，六边形是⊙的内接正六边形，点为弧BC上一动点，请探究三者之间有何数量关系，并给予证明.‎ 图1‎ 图2‎ 图3‎ ‎ ‎ ‎25.（本题满分8分）‎ 如图，菱形OABC的顶点O在坐标原点，顶点B在x轴的正半轴上，OA边在直线 上，AB边在直线上。‎ ‎（1）直接写出O、A、B、C的坐标；‎ ‎（2）在OB上有一动点P，以O为圆心，OP为半径画弧，分别交边OA、OC于 M、N（M、N可以与A、C重合），作⊙Q与边AB、BC，弧都相切，⊙Q分别与边AB、BC相切于点D、E，设⊙Q的半径为 r，OP的长为y，求y与r之间的函数关系式，并写出自变量r的取值范围；‎ ‎（3）以O为圆心、OA为半径做扇形OAC，请问在菱形OABC中，除去扇形OAC后剩余部分内，是否可以截下一个圆，使得它与扇形OAC刚好围成一个圆锥. 若可以，求出这个圆的面积，若不可以，说明理由。‎ ‎（第25题图）‎ 参考答案及评分标准 ‎ 一、选择题（共8道小题，每小题4分，共32分） ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A C D A C B A ‎ D 二、填空题（共4道小题，每小题4分，共16分）‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 ‎ ‎ ‎ ‎ ‎,；‎ 三、解答题（共13道小题，共72分）‎ ‎13.解：原式= ……………………………………………………………4分 ‎=………………………………………………………………………………… 5分 ‎14.解：方程两边同乘，得 ‎． 3分 解这个方程，得 ‎． 4分 检验：当时，．‎ 所以是原方程的解． 5分 ‎15. 解：在Rt△BCD中，CD=BC×sin60°=20× …………………………………3分 又∵DE=AB=1.5‎ ‎∴CE=CD＋DE=(米)‎ 答：此时风筝离地面的高度约是‎18.8米.…………………………………………5分 ‎16.解： ‎ ‎………3分 D E ‎（第17题）‎ A B O ‎…………………5分 ‎ ‎17． 解：（1）画图正确（如图）．…………2分 ‎（2）所扫过的面积是：‎ ‎．…………5分 ‎18．（1）证明：∵为半圆的直径，‎ ‎∴ ‎ 又∵∥， ∴，‎ ‎∴.‎ ‎∵， ∴.‎ ‎∴半径OA⊥AD于点A，∴是半圆O的切线. …………………2分 ‎ （2）解：∵在⊙O中，于E， ∴.‎ ‎ 在中，，. …3分 ‎ ∵，‎ ‎∴∽：‎ ‎∴, ∴‎ ‎∴ ………………………………………………………………………5分 ‎19．证法一：连结CD ‎∵ DE∥AC，DF∥BC，‎ ‎∴ 四边形DECF为平行四边形，‎ ‎∵∠CAB、∠ABC的平分线交于点D ‎∴点D是△ABC的内心，‎ ‎∴ CD平分∠ACB，即∠FCD＝∠ECD，‎ ‎∵DF∥BC ‎∴∠FDC＝∠ECD，∴ ∠FCD＝∠FDC ‎ ‎∴ FC＝FD，‎ ‎∴ 平行四边形DECF为菱形． 5分 证法二：过D分别作DG⊥AB于G，DH⊥BC于H，DI⊥AC于I．‎ ‎∵AD、BD分别平分∠CAB、∠ABC，‎ ‎∴DI=DG，DG=DH．∴DH=DI．‎ ‎∵DE∥AC，DF∥BC，‎ ‎∴四边形DECF为平行四边形，‎ ‎∴S□DECF=CE·DH =CF·DI，‎ ‎∴CE=CF．‎ ‎∴平行四边形DECF为菱形．…………………5分 ‎20. （1）4％. …………………………………………………………………………… 1分 ‎（2）. ………………………………………………………………………… 2分 ‎（3）B级．……………………………………………………………………………… 3分 ‎（4）由题意可知，A级和B级学生的人数和占全班总人数的%，‎ ‎∴%.‎ ‎∴估计这次考试中A级和B级的学生共有380人.………………………5分 ‎21．解：（1）设与之间的关系为一次函数，其函数表达式为…………1分 将，代入上式得，‎ ‎ 解得 ‎ 3分 验证：当时，，符合一次函数；‎ 当时，，也符合一次函数．‎ 可用一次函数表示其变化规律，而不用反比例函数、二次函数表示其变化规律 与之间的关系是一次函数，其函数表达式为 4分 ‎（2）当时，由可得 即货车行驶到B处时油箱内余油‎16升．……………………………………… 5分 ‎22．解：（1）特征数为的一次函数为，‎ ‎，‎ ‎．………………………………………………………………………1分 ‎（2）抛物线与轴的交点为，与轴的交点为．‎ 若，则，∴（舍）；‎ 若，则，∴．‎ 综上，．‎ 抛物线为，它与轴的交点为，与轴的交点为，所求一次函数为或，‎ 特征数为或………………………………………………5分 ‎23. 解：（1）由，可知抛物线C1的顶点为M（－2，－1）．由图知点M（－2，－1）关于点R（1，0）中心对称的点为N（4，1），以N（4，1）为顶点，与抛物线C1关于点R（1，0）中心对称的图像C2也是抛物线，且C1与C2的开口方向相反，故抛物线C2的函数解析式为，‎ 即． …………………………………………………3分 ‎（2）令=0，得抛物线C1、C2与y轴的交点A、B的纵坐标分别为和.‎ ‎∴．‎ ‎ ∴．‎ 当时，有，得；‎ 当<时，有，得． ……………………………………7分 ‎24. (1)证明：延长至,使,连结CE.‎ 是等边三角形.‎ 又 ‎ .…………2分 ‎(2) 证明：过点作交于,‎ ‎,‎ 又，‎ 又.‎ ‎ …………………………………………………4分 ‎(3)答:‎ 证明：在上截取,连结,‎ ‎,‎ ‎.‎ 又，‎ ‎ …………………………………………………7分 ‎25.解：（1），，，；………………………… 2分 ‎ （2）连结QD、QE，则QD⊥AB，QE⊥BC.‎ ‎∵QD=QE，∴点Q在的平分线上.‎ 又∵OABC是菱形，∴点Q在OB上. ∴⊙Q与弧MN相切于点P.‎ 在Rt⊿QDB中，,‎ ‎∴QB=2QD=2r. ∴， .‎ 其中.………………………………………………… 5分 ‎ （3）可以. 理由：弧的长为.‎ 设截下的⊙G符合条件，其半径为R，则..‎ 由（2）知，此时，则⊙Q的半径，‎ 能截下一个圆，使得它与扇形OAC刚好围成一个圆锥，‎ 此圆的面积为.………………………………………………8分