2019届中考数学一轮复习 第31课时 函数与方程思想导学案（无答案） 5页

第31课时 函数与方程思想 班级： 姓名： ‎ 学习目标：1.探索实际生活中的数量关系和变化规律.‎ ‎2.利用函数的性质或方程理论解决有关实际问题.‎ 重难点：利用函数的性质或方程理论解决有关实际问题.‎ 学习过程 一．知识梳理 一次函数：‎ 一次函数 的图像与轴的交点坐标为 ，与轴的交点坐标为 ‎ 当时，随的增大而 ，图象一定经过第 象限；‎ 当时，随的 而减小，图象一定经过第 象限．‎ 二次函数：‎ 抛物线，当时，抛物线转化为一元二次方程 , ‎ 该方程的根是抛物线与 的交点横坐标。‎ 变式：抛物线，当时，抛物线转化为一元二次方程 ，‎ 该方程的根是抛物线与 的交点横坐标。‎ 二、典型例题 ‎1.函数与方程、不等式 ‎（1）如图，正比例函数与反比例函数相交于点，若，则的取值范围在数轴上表示正确的是（　　）‎ A． B． ‎ C． D．‎ ‎（2）如图，函数，．当时，x的范围是（ ）‎ ‎ A.． B． C． D．‎ ‎（3）如图，是二次函数图象的一部分，其对称轴为直线，若其与轴一交点为，则由图象可知，不等式的解集是 .‎ ‎（4）如图是二次函数的图象，且关于的一元二次方程没有实数根，则的取值范围是 ‎ 5‎ ‎2.函数的实际应用 ‎（中考指要例1）（2017湖州）湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了‎20000kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本=放养总费用+收购成本）． （1）设每天的放养费用是万元，收购成本为万元，求和的值； （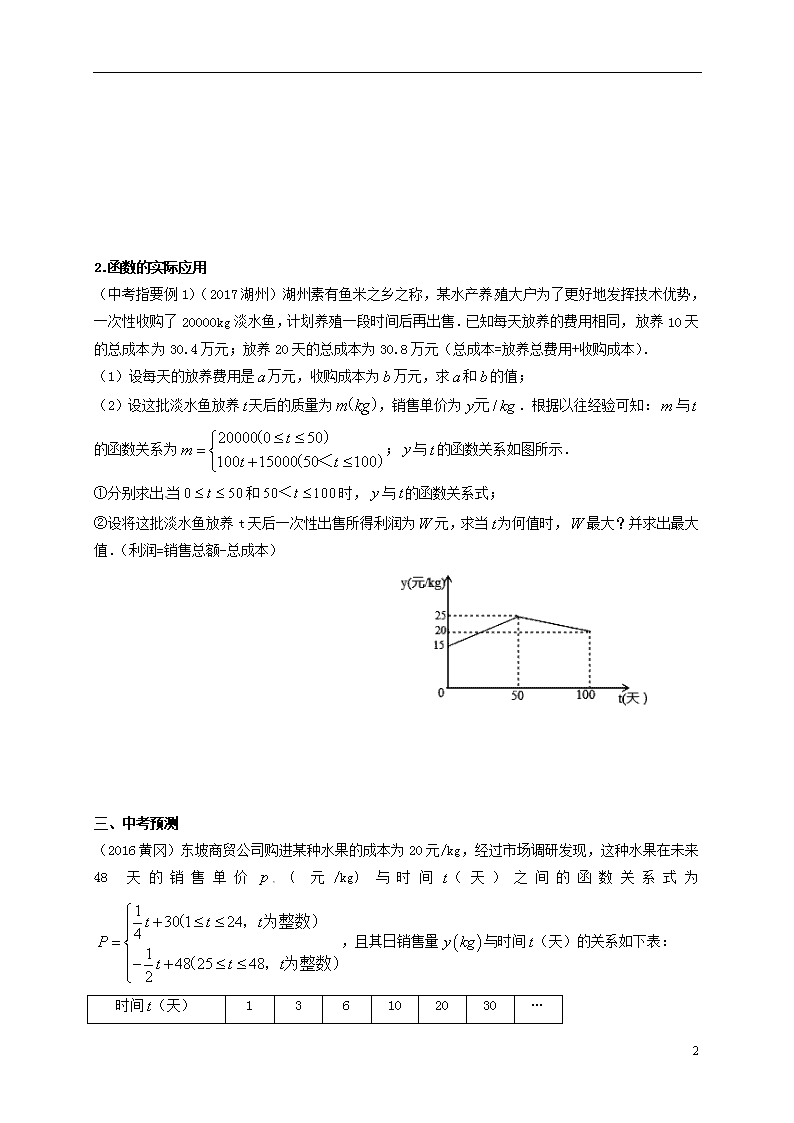2）设这批淡水鱼放养天后的质量为，销售单价为．根据以往经验可知：与的函数关系为；与的函数关系如图所示． ①分别求出当和时，与的函数关系式； ②设将这批淡水鱼放养t天后一次性出售所得利润为元，求当为何值时，最大？并求出最大值．（利润=销售总额-总成本）‎ 三、中考预测 ‎（2016黄冈）东坡商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价 (元/kg)与时间（天）之间的函数关系式为，且其日销售量与时间（天）的关系如下表：‎ 时间（天）‎ ‎1‎ ‎3‎ ‎6‎ ‎10‎ ‎20‎ ‎30‎ ‎…‎ 5‎ 日销售量 ‎118‎ ‎114‎ ‎108‎ ‎100‎ ‎80‎ ‎40‎ ‎…‎ ‎（1）已知与之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？‎ ‎（2）问哪一天的销售利润最大？最大日销售利润为多少？‎ ‎（3）在实际销售的前24天中，公司决定每销售‎1kg水果就捐赠元利润给“精准扶贫”对象。现发现：在前24天中，每天扣除捐赠后的日销售利润随时间的增大而增大，求的取值范围。‎ 四、反思总结 ‎1.本节课你复习了哪些内容？‎ ‎2.通过本节课的学习，你还有哪些困难？‎ 五、达标检测 ‎1.若函数的图象与轴有且只有一个交点，则的值为________．‎ ‎2.(2016·常州)已知一次函数和二次函数的自变量和对应函数值如表：‎ x ‎…‎ ‎－1‎ ‎0‎ ‎2‎ ‎4‎ ‎…‎ y1‎ ‎…‎ ‎0‎ ‎1‎ ‎3‎ ‎5‎ ‎…‎ x ‎…‎ ‎－1‎ ‎1‎ ‎3‎ ‎4‎ ‎…‎ y2‎ ‎…‎ ‎0‎ ‎－4‎ ‎0‎ ‎5‎ ‎…‎ 当时，自变量x的取值范围是(　　)‎ A． B． C． D．‎ ‎3.已知函数和.‎ ‎（1）若这两个函数的图像都经过点，求的值；‎ ‎（2)当取何值时，这两个函数的图像总有公共点？‎ 5‎ ‎4.如图，已知关于的二次函数的图像经过原点O，并且与轴交于点，对称轴为直线．‎ ‎（1）常数 ，点的坐标为 ；‎ ‎（2）若关于的一元二次方程（为常数）有两个不相等的实数根，求的取值范围； ‎ O y x A ‎（3）若关于的一元二次方程（为常数）在的范围内有解，求的取值范围．‎ ‎5.（2016高邮一模）小王经营的蛋品直销店中，某种鸭蛋的进价为40元/盒，售价为60元/盒，每月可卖出300盒．经市场调研发现：售价在60元/盒的基础上每涨1元每月要少卖10盒；售价每下降1元每月要多卖20盒．为了获得更大的利润，现将售价调整为元/盒（x＞0即售价上涨，x＜0即售价下降），每月销售量为y盒，月利润为w元．‎ ‎（1）①当x＞0时，y与x之间的函数关系式是______，②当x＜0时，y与x之间的函数关系式是______；‎ ‎（2）求售价定为多少元/盒时，才能使月利润w最大？月利润最大是多少？‎ ‎（3）为了使这种鸭蛋销售的月利润不少于6000元，售价应在什么范围内？‎ 5‎ ‎6.（中考指要P144）（2017扬州）农经公司以30元/千克的价格收购一批农产品进行销售，为了得到日销售量（千克）与销售价格（元/千克）之间的关系，经过市场调查获得部分数据如下表：‎ 销售价格（元/千克）‎ ‎30‎ ‎35‎ ‎40‎ ‎45‎ ‎50‎ 日销售量（千克）‎ ‎600‎ ‎450‎ ‎300‎ ‎150‎ ‎0‎ ‎（1）请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定与之间的函数表达式；‎ ‎（2）农经公司应该如何确定这批农产品的销售价格，才能使日销售利润最大？ （3）若农经公司每销售‎1千克这种农产品需支出元（）的相关费用，当时，农经公司的日获利的最大值为2430元，求的值．（日获利=日销售利润-日支出费用）‎ 5‎