中考数学专题练习——圆 5页

中考数学专题练习《圆》‎ ‎【知识归纳】‎ 1、 圆的有关的性质 ‎（1）圆既是轴对称图形又是中心对称图形。‎ ‎（2）垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。‎ ‎（3）圆周角定理：圆周角的度数等于它所对弧上的圆心角的一半，同弧或等弧所对的圆周 ‎ 角相等 ‎ 推论：①直径所对的圆周角是直角，90°的圆周角所对的弦是直径。‎ ‎ ② 圆内接四边形对角互补。‎ ‎2、与圆有关的位置关系 ‎（1）点与圆的位置关系（圆的半径为 r，点 p 到圆心的距离是d 点在圆外：d＞r 点在圆上：d = r 点在圆内：d＜r ‎（2）直线与圆的位置关系（圆的半径为 r，直线 l 到圆心的距离是d 直线与圆相交：d＜r 直线与圆相切：d = r 直线与圆相离：d＞r （3） 圆的切线（遇到切线连半径）‎ ‎ 切线的判定：经过半径的外端并且垂直于这条半径的直线是圆的切线 ‎ 切线的性质：圆的切线垂直于经过切点的半径 ‎ ‎ 圆的切线切线长及切线长定理：过圆外一点所画圆的两条切线长相等，圆心和这一点 ‎ ‎ 的连线平分两条切线的夹角。‎ ‎（4）三角形的内切圆（如右图）‎ ‎①∠BIC = ∠BAC + 90°‎ ‎ ②内切圆半径为 r，S△ABC = r（a+b+c）‎ ‎3、与圆有关的计算 ‎（1）弧长的计算 ‎ L= = ‎ ‎ （2）扇形面积 S扇 = πR² S扇 = ‎ （3） 圆锥的侧面积 S = =πrl 圆中常用辅助线的作法： 圆是初中几何部分的重要内容之一，与圆有关的大部分几何题型都需要添加辅助线来解决。只要添上合适的辅助线，不仅会使问题迎刃而解，而且还会有效地培养学生的解题能力与创造性思维能力。通过对实践教学中的归纳与总结，发现添加辅助线的方法有很多，就圆中常见作辅助线的方法归纳如下： 一、作弦心距（在与弦有关的计算或证明题时，常作辅助线的方法是作弦心距） 二、连半径（与半径和弦有关的简单计算、已知圆中有切线的有关计算和证明时，常作辅助线的方法是连半径） 三、既作弦心距又连半径（与半径和弦都有关的计算时，常作辅助线的方法是既作弦心距又连半径，利用勾股定理来解决） 四、连弦构造相似三角形或直角三角形（在圆中与弦或其他有关的计算或证明时，常作辅助线的方法是连弦，利用同弧所对的圆周角相等连弦构造相似三角形或利用直径所对的圆周角为直角这个性质连弦构造出直角三角形，从而将问题转化到相似三角形或直角三角形中去计算或证明） 五、作直径构造直角三角形（在圆中牵涉到三角函数的运算或与直径的计算与证明时，常作辅助线的方法是作直径，利用直径所对的圆周角是直角构造直角三角形，从而将问题转化到直角三角形中去解决）      总之，在解答几何问题时，辅助线添加是非常关键的，辅助线是沟通题设和结论的桥梁，也是解答几何问题的重要手段。然而，添加辅助线则是几何学习的一个难点。因此，能正确地添加辅助线，会使问题迎刃而解，这不仅调动了学习的积极性、学习兴趣，而且开发了智力，掌握了解题技能和技巧，提高了解题的效率。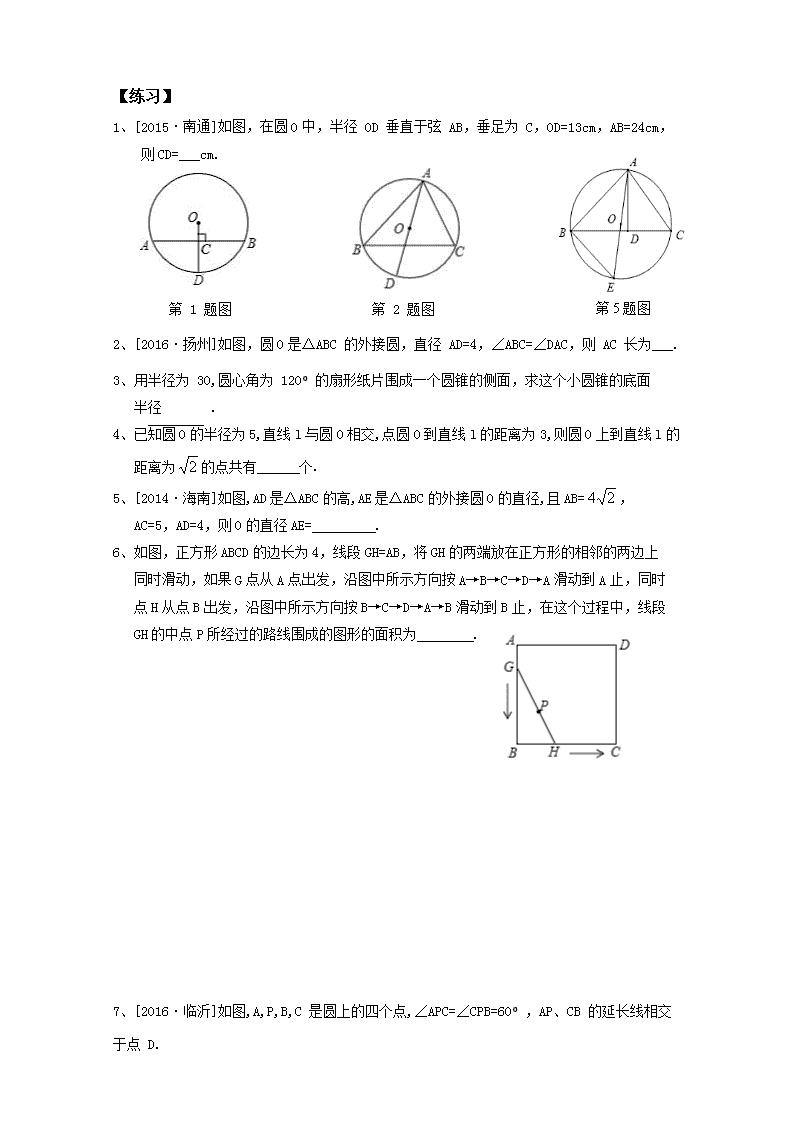 ‎ ‎【练习】‎ 1、 ‎[2015·南通]如图，在圆O中，半径 OD 垂直于弦 AB，垂足为 C，OD=13cm，AB=24cm， ‎ ‎ 则CD=___cm.‎ ‎ ‎ 第5题图 ‎ 第 1 题图 第 2 题图 2、 ‎[2016·扬州]如图，圆O是△ABC 的外接圆，直径 AD=4，∠ABC=∠DAC，则 AC 长为___. ‎ ‎3、用半径为 30,圆心角为 120∘ 的扇形纸片围成一个圆锥的侧面，求这个小圆锥的底面 ‎ 半径 ．‎ ‎4、已知圆O的半径为5,直线l与圆O相交,点圆O到直线l的距离为3,则圆O上到直线l的 ‎ ‎ 距离为的点共有 个.‎ 5、 ‎[2014·海南]如图,AD是△ABC的高,AE是△ABC的外接圆O的直径,且AB=， ‎ ‎ AC=5，AD=4，则O的直径AE= .‎ ‎6、如图，正方形ABCD的边长为4，线段GH=AB，将GH的两端放在正方形的相邻的两边上 ‎ ‎ 同时滑动，如果G点从A点出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时 ‎ ‎ 点H从点B出发，沿图中所示方向按B→C→D→A→B滑动到B止，在这个过程中，线段 ‎ GH的中点P所经过的路线围成的图形的面积为 .‎ ‎7、[2016·临沂]如图,A,P,B,C 是圆上的四个点,∠APC=∠CPB=60∘ ，AP、CB 的延长线相交于点 D.‎ ‎(1)求证：△ABC 是等边三角形；‎ ‎(2)若∠PAC=90∘ ,AB= ，求 PD 的长。‎ ‎8、[2011，徐州]如图，PA，PB是圆O的两条切线，切点分别为A、B,OP交AB于点C， ‎ ‎ OP=13，sin∠APC=‎ ‎ (1)求圆O的半径；‎ ‎ (2)求弦AB的长。‎ 9、 ‎[2016·威海]如图，在△BCE 中，点 A 是边 BE 上一点，以 AB 为直径的圆O与 CE 相 ‎ ‎ 切于点 D，AD∥ OC，点 F为 OC 与 圆O的交点，连接 AF.‎ ‎ (1)求证：CB 是 圆O的切线；‎ ‎ (2)若∠ECB=60° ，AB=6，求图中阴影部分的面积。‎