2020中考数学复习 第24课时 矩形、菱形、正方形（无答案） 3页

第24课时 矩形、菱形、正方形 ‎【课前热身】‎ ‎1. 矩形的两条对角线的一个交角为60 o，两条对角线的长度的和为‎8cm，则这个矩形的一条较短边为 cm.‎ ‎2.边长为‎５cm的菱形，一条对角线长是‎6cm，则另一条对角线的长是 .‎ ‎3. 若正方形的一条对角线的长为‎2cm，则这个正方形的面积为 ．‎ ‎4．在平面中，下列命题为真命题的是（　　）‎ A．四边相等的四边形是正方形　　B．对角线相等的四边形是菱形　‎ ‎　C．四个角相等的四边形是矩形　　D．对角线互相垂直的四边形是平行四边形 考点梳理 考点一 矩形的定义、性质和判定 1. 定义：有一个角是直角的平行四边形是矩形。‎ 2. 性质：‎ ‎（1）矩形的四个角都是直角；‎ ‎（2）矩形的对角线 ；‎ ‎(3)矩形既是轴对称图形，又是中心对称图形，它有 条对称轴；它的对称中心是 .‎ ‎3.判定：‎ ‎（1）有 的平行四边形是矩形；‎ ‎（2）有 的四边形是矩形；‎ ‎（3）对角线 平行四边形是矩形。‎ 考点二 菱形的定义、性质和判定 1. 定义：有一组邻边相等的平行四边形是菱形。‎ 2. 性质：（1）菱形的四边 ，对角线互相 ，并且每条对角线 ‎ ‎ （2）菱形既是轴对称图形，又是中心对称图形。‎ ‎3.判定：（1）有 的平行四边形是菱形；‎ ‎（2） 四边形是菱形；‎ ‎（3）对角线 的平行四边形是菱形。‎ 考点二 正方形的定义、性质和判定 1. 定义：有一个角是直角的菱形是正方形或有一组邻边相等的矩形是正方形。‎ 3‎ 1. 性质：（1）正方形四个角都是 ，四条边 ；‎ ‎ （2）正方形两条对角线 ，并且每条对角线平分一组对角。‎ ‎3.判定：（1）有一个角是直角的菱形是正方形；‎ ‎ （2）有一组邻边相等的矩形是正方形。‎ ‎【典型例题】‎ 例1.如图，在△ABC中，AB=AC，D为边BC上一点，以AB,BD为邻边作平行四边形ABDE，连接AD，EC．‎ ‎（1）求证：△ADC△ECD；‎ ‎（2）若BD=CD,求证四边形ADCE是矩形．‎ 例2.如图，已知⊿ABC，按如下步骤作图：①分别以A、C为圆心，以大于AC的长为半径在AC两边作弧，交于两点M、N；②连接MN，分别交AB、AC于点D、O；③过C作CE//AB交MN于点E，连接AE、CD。‎ ‎（1）求证：四边形ADCE是菱形；‎ ‎（2）当∠ACB=90°，BC=6，⊿ADC的周长为18时，求四边形ADCE的面积。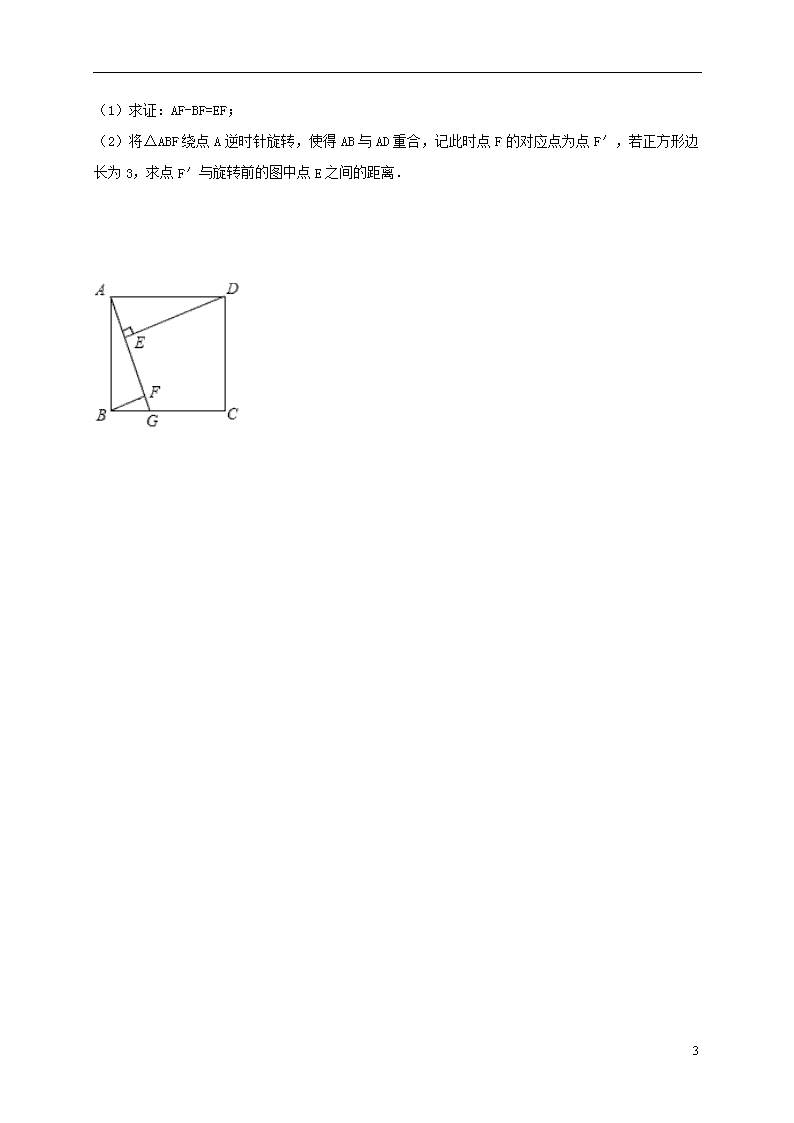‎ 例3.‎ 3‎ 如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于E，BF∥DE，交AG于F． （1）求证：AF-BF=EF； （2）将△ABF绕点A逆时针旋转，使得AB与AD重合，记此时点F的对应点为点F′，若正方形边长为3，求点F′与旋转前的图中点E之间的距离．‎ 3‎