中考数学压轴题12套1 9页

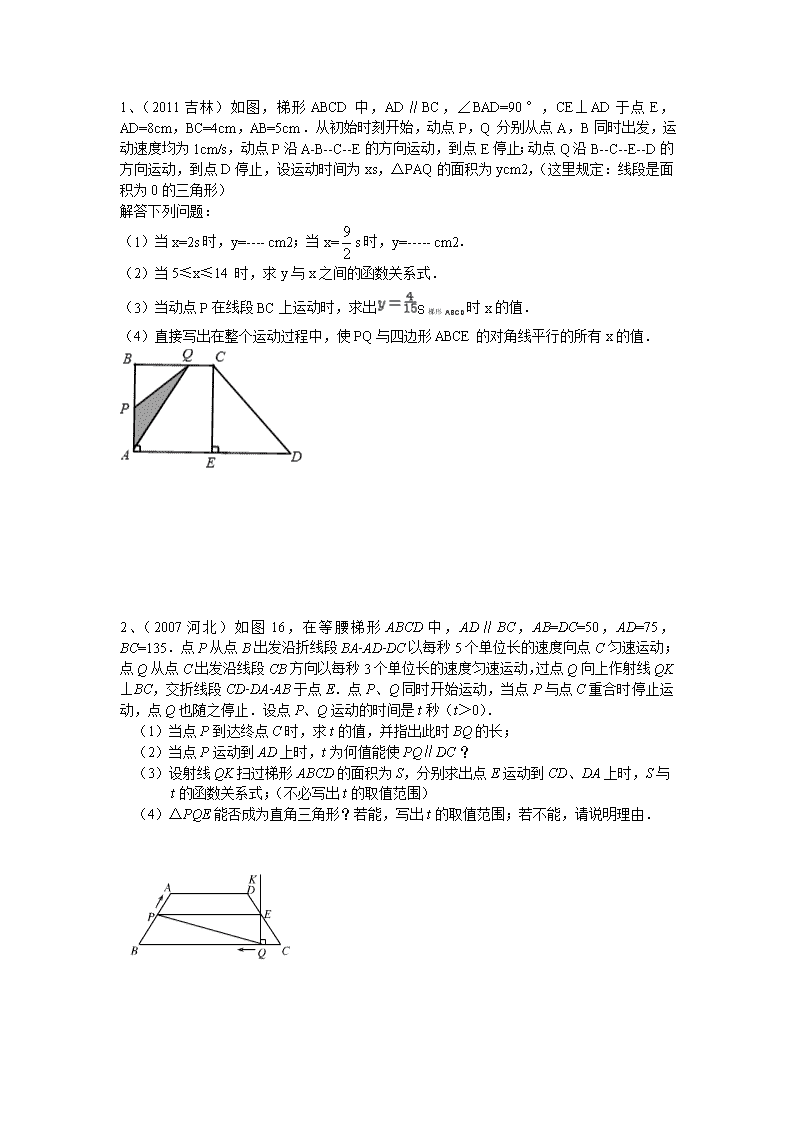
1、（2011 吉林）如图，梯形 ABCD 中，AD∥BC，∠BAD=90°，CE⊥AD 于点 E，AD=8cm， BC=4cm，AB=5cm．从初始时刻开始，动点 P，Q 分别从点 A，B 同时出发，运动速度均 为 1cm/s，动点 P 沿 A-B--C--E 的方向运动，到点 E 停止；动点 Q 沿 B--C--E--D 的方向运动， 到点 D 停止，设运动时间为 xs，△PAQ 的面积为 ycm2，（这里规定：线段是面积为 0 的三 角形） 解答下列问题： （1）当 x=2s 时，y=---- cm2；当 x= 2 9 s 时，y=----- cm2． （2）当 5≤x≤14 时，求 y 与 x 之间的函数关系式． （3）当动点 P 在线段 BC 上运动时，求出 S 梯形 ABCD 时 x 的值． （4）直接写出在整个运动过程中，使 PQ 与四边形 ABCE 的对角线平行的所有 x 的值． 2、（2007 河北）如图 16，在等腰梯形 ABCD 中，AD∥BC，AB=DC=50，AD=75，BC=135．点 P 从点 B 出发沿折线段 BA-AD-DC 以每秒 5 个单位长的速度向点 C 匀速运动；点 Q 从点 C 出发沿线段 CB 方向以每秒 3 个单位长的速度匀速运动，过点 Q 向上作射线 QK⊥BC，交折 线段 CD-DA-AB 于点 E．点 P、Q 同时开始运动，当点 P 与点 C 重合时停止运动，点 Q 也 随之停止．设点 P、Q 运动的时间是 t 秒（t＞0）． （1）当点 P 到达终点 C 时，求 t 的值，并指出此时 BQ 的长； （2）当点 P 运动到 AD 上时，t 为何值能使 PQ∥DC ？ （3）设射线 QK 扫过梯形 ABCD 的面积为 S，分别求出点 E 运动到 CD、DA 上时，S 与 t 的函数关系式；（不必写出 t 的取值范围） （4）△PQE 能否成为直角三角形？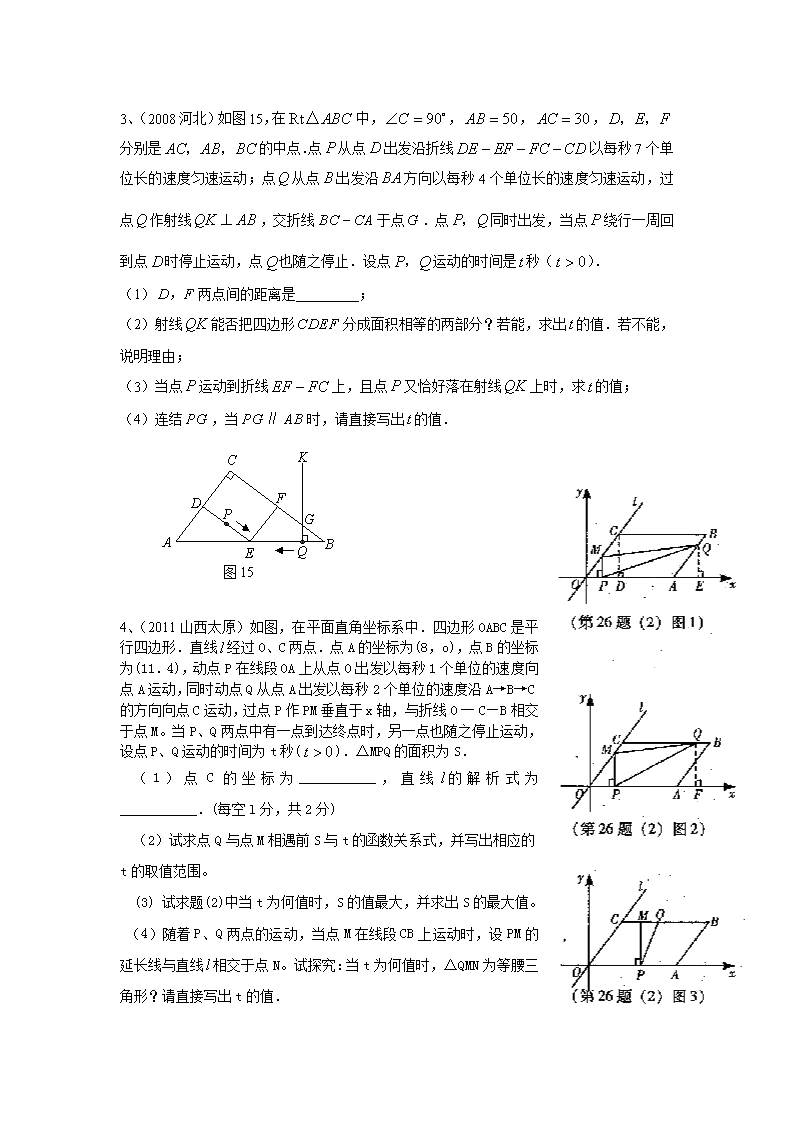若能，写出 t 的取值范围；若不能，请说明理由． 3、（2008 河北）如图 15，在 Rt ABC△ 中， 90C   ， 50AB  ， 30AC  ，D E F， ， 分别是 AC AB BC， ， 的中点．点 P 从点 D 出发沿折线 DE EF FC CD   以每秒 7 个单 位长的速度匀速运动；点 Q 从点 B 出发沿 BA 方向以每秒 4 个单位长的速度匀速运动，过 点Q 作射线QK AB ，交折线 BC CA 于点G ．点 P Q， 同时出发，当点 P 绕行一周回 到点 D 时停止运动，点Q 也随之停止．设点 P Q， 运动的时间是t 秒（ 0t  ）． （1） D F， 两点间的距离是 ； （2）射线 QK 能否把四边形 CDEF 分成面积相等的两部分？若能，求出t 的值．若不能， 说明理由； （3）当点 P 运动到折线 EF FC 上，且点 P 又恰好落在射线QK 上时，求t 的值； （4）连结 PG ，当 PG AB∥ 时，请直接．．写出t 的值． 4、（2011 山西太原）如图，在平面直角坐标系中．四边形 OABC 是平 行四边形．直线l 经过 O、C 两点．点 A 的坐标为(8，o)，点 B 的坐标 为(11．4)，动点 P 在线段 OA 上从点 O 出发以每秒 1 个单位的速度向 点 A 运动，同时动点 Q 从点 A 出发以每秒 2 个单位的速度沿 A→B→C 的方向向点 C 运动，过点 P 作 PM 垂直于 x 轴，与折线 O 一 C—B 相交 于点 M。当 P、Q 两点中有一点到达终点时，另一点也随之停止运动， 设点 P、Q 运动的时间为 t 秒( 0t  )．△MPQ 的面积为 S． （1）点 C 的坐标为___________，直线 l 的解析式为___________．(每 空 l 分，共 2 分) （2）试求点 Q 与点 M 相遇前 S 与 t 的函数关系式，并写出相应的 t 的取值范围。 (3) 试求题(2)中当 t 为何值时，S 的值最大，并求出 S 的最大值。 （4）随着 P、Q 两点的运动，当点 M 在线段 CB 上运动时，设 PM 的 延长线与直线l 相交于点 N。试探究：当 t 为何值时，△QMN 为等腰三 角形？请直接写出 t 的值． A E C D F G BQ K 图 15 P 5、（2011 四川重庆）如图，矩形 ABCD 中，AB=6，BC= 2 3 ，点 O 是 AB 的中点，点 P 在 AB 的延长线上，且 BP=3。一动点 E 从 O 点出发，以每秒 1 个单位长度的速度沿 OA 匀速运动， 到达 A 点后，立即以原速度沿 AO 返回；另一动点 F 从 P 点发发，以每秒 1 个单位长度的速 度沿射线 PA 匀速运动，点 E、F 同时出发，当两点相遇时停止运动，在点 E、F 的运动过程 中，以 EF 为边作等边△EFG，使△EFG 和矩形 ABCD 在射线 PA 的同侧。设运动的时间为 t 秒 （t≥0）。 （1）当等边△EFG 的边 FG 恰好经过点 C 时，求运动时间 t 的值； （2）在整个运动过程中，设等边△EFG 和矩形 ABCD 重叠部分的面积为 S，请直接写出 S 与 t 之间的函数关系式和相应的自变量 t 的取值范围； （3）设 EG 与矩形 ABCD 的对角线 AC 的交点为 H，是否存在这样的 t ,使△AOH 是等腰三角 形？若存大，求出对应的 t 的值；若不存在，请说明理由。 1、解：（1） 2；9、 （2） 当 5≤ x ≤9 时 y= S 梯形 ABCQ –S△ABP –S△PCQ = 2 1 (5+ x -4)×4 2 1 ×5( x -5) 2 1 (9- x )( x -4) 2 6572 1 2  xx 2 6572 1 2  xxy 当 9＜ x ≤13 时 y= 2 1 （ x -9+4）(14- x ) 352 19 2 1 2  xx 352 19 2 1 2  xxy 当 13＜ x ≤14 时 y= 2 1 ×8(14- x )=-4 x +56 即 y=-4 x +56 （3） 当动点 P 在线段 BC 上运动时， ∵ 15 4y S 梯形 ABCD 15 4 × 2 1 (4+8)×5 = 8 即 x ²-14 x +49 = 0 解得 x 1 = x 2 = 7 ∴当 x =7 时， 15 4y S 梯形 ABCD （4） 9 101 9 61 9 21x 说明：（1）自变量取值不含 9，13 可不扣分 2、解：（1）t =（50＋75＋50）÷5=35（秒）时，点 P 到达终点 C． ……………（1 分） 此时，QC=35×3=105，∴BQ 的长为 135－105=30． ………………（2 分） （2）如图 8，若 PQ∥DC，又 AD∥BC，则四边形 PQCD 为平行四边形，从而 PD=QC，由 QC=3t，BA+AP=5t 得 50＋75－5t=3t，解得 t= 125 8 ． 经检验，当 t= 125 8 时，有 PQ∥DC．………（4 分） （3）①当点 E 在 CD 上运动时，如图 9．分别过点 A、D 作 AF⊥BC 于点 F，DH⊥BC 于点 H，则四边形 ADHF 为矩形，且△ABF≌△DCH，从而 FH= AD=75，于是 BF=CH=30．∴DH=AF=40． 又 QC=3t，从而 QE=QC·tanC=3t· CH DH =4t． ∴S=S⊿QCE = 1 2 QE·QC=6t2； ………………………………………………………（6 分） ②当点 E 在 DA 上运动时，如图 8．过点 D 作 DH⊥BC 于点 H，由①知 DH=40，CH=30，又 QC=3t，从而 ED=QH=QC－CH=3t－30． ∴S= S 梯形 QCDE = 1 2 (ED＋QC)DH =120 t－600． …………………………（8 分） （4）△PQE 能成为直角三角形． ……………………………………………………（9 分） 当△PQE 为直角三角形时，t 的取值范围是 0＜t≤25 且 t≠ 155 8 或 t=35． …（12 分） （注：（4）问中没有答出 t≠ 155 8 或 t=35 者各扣 1 分，其余写法酌情给分） 下面是第（4）问的解法，仅供教师参考： ①当点 P 在 BA（包括点 A）上，即 0＜t≤10 时，如图 9．过点 P 作 PG⊥BC 于点 G ，则 PG=PB·sinB=4t，又有 QE=4t = PG，易得四边形 PGQE 为矩形，此时△PQE 总能成为 直角三角形． ②当点 P、E 都在 AD（不包括点 A 但包括点 D）上，即 10＜t≤25 时，如图 8． 由 QK⊥BC 和 AD∥BC 可知，此时，△PQE 为直角三角形，但点 P、E 不能重合，即 5t－50＋3t－30≠75，解得 t≠ 155 8 ． ③当点 P 在 DC 上（不包括点 D 但包括点 C）， 即 25＜t≤35 时，如图 10．由 ED＞25×3－30=45， 可知，点 P 在以 QE=40 为直径的圆的外部，故 ∠EPQ 不会是直角． 由∠PEQ＜∠DEQ，可知∠PEQ 一定是锐角． 对于∠PQE，∠PQE≤∠CQE，只有当点 P 与 C 重合，即 t=35 时，如图 11，∠PQE=90°，△PQE 为直角三角形． 综上所述，当△PQE 为直角三角形时，t 的取值范围是 0＜t≤25 且 t≠ 155 8 或 t=35． 3、解：（1）25．（2）能． 如图 5，连结 DF ，过点 F 作 FH AB 于点 H ，由四边形CDEF 为矩形，可知QK 过 DF 的中点O 时，QK 把矩形CDEF 分为面积相等的两部分（注：可利用全等三角形借助割补 法或用中心对称等方法说明）， 此时 12.5QH OF  ．由 20BF  ， HBF CBA△ ∽△ ，得 16HB  ． 故 12.5 16 174 8t   ． （3）①当点 P 在 EF 上 6(2 5)7 t≤ ≤ 时，如图 6． 4QB t ， 7DE EP t  ， 由 PQE BCA△ ∽△ ，得 7 20 25 4 50 30 t t  ． 214 41t  ． ②当点 P 在 FC 上 6(5 7 )7t≤ ≤ 时，如图 7． 已知 4QB t ，从而 5PB t ， 由 7 35PF t  ， 20BF  ，得5 7 35 20t t   ． 解得 17 2t  ． （4）如图 8， 213t  ；如图 9， 397 43t  ． （注：判断 PG AB∥ 可分为以下几种情形：当 60 2 7t ≤ 时，点 P 下行，点G 上行，可知其中存在 PG AB∥ 的时刻， 如图 8；此后，点G 继续上行到点 F 时， 4t  ，而点 P 却在 下行到点 E 再沿 EF 上行，发现点 P 在 EF 上运动时不存在 PG AB∥ ；当 65 7 7t≤ ≤ 时，点 P G， 均在 FC 上，也不 存在 PG AB∥ ；由于点 P 比点 G 先到达点C 并继续沿 CD 下行，所以在 67 87 t  中存在 PG AB∥ 的时刻，如图 9；当8 10t≤ ≤ 时，点 P G， 均 在CD 上，不存在 PG AB∥ ） 4、解：(1)(3,4)； 4 3y x (2)根据题意，得 OP=t，AQ=2t．分三种情况讨论： ①当 50 2t  时，如图 l，M 点的坐标是（ 4 3t t， ）． 过点 C 作 CD⊥x 轴于 D，过点 Q 作 QE⊥ x 轴于 E，可得△AEO∽△ODC ∴ AQ AE QE OC OD CD   ，∴ 2 AE QE= =5 3 4 t ，∴ 6 5 tAE  ， 8 5EQ t ∴Q 点的坐标是（ 6 88 5 5t t ， ），∴PE= 6 18 85 5t t t    A E C D F BQ K 图 6 P G A E C D F BQ K 图 7 P(G) A E C D F BQ K 图 8 P G H A E C D F BQ K 图 9 P G ∴S= 21 1 4 1 2 16(8 )2 2 3 5 15 3MP PE t t t t        ②当 5 32 t  时，如图 2，过点 q 作 QF⊥x 轴于 F， ∵ 2 5BQ t  ，∴OF=11 (2 5) 16 2t t    ∴Q 点的坐标是（16 2 4t ， ），∴PF=16 2 16 3t t t    ∴S= 21 1 4 32(16 3 ) 22 2 3 3MP PF t t t t         ③当点 Q 与点 M 相遇时，16 2t t  ，解得 16 3t  。 ③当 163 3t  时，如图 3，MQ=16 2 16 3t t t    ，MP=4. S= 1 1 4 (16 3 ) 6 322 2MP PF t t         (3)① 当 50 2t  时， 2 22 16 2 160( 20)15 3 15 3S t t t     ∵ 2 015a   ，抛物线开口向上，对称轴为直线 20t   ， ∴ 当 50 2t  时，S 随 t 的增大而增大。 ∴ 当 5 2t  时，S 有最大值，最大值为 85 6 ． ②当 5 32 t  时， 2 232 8 1282 2( )3 3 9S t t t       。∵ 2 0a    ，抛物线开口向 下． ∴当 8 3t  时，S 有最大值，最大值为128 9 ． ③当 163 3t  时， 6 32S t   ，∵ 6 0k    ．∴S 随 t 的增大而减小． 又∵当 3t  时，S=14．当 16 3t  时，S=0．∴ 0 14S  ． 综上所述，当 8 3t  时，S 有最大值，最大值为128 9 。 (4)当 60 13t  时，△QMN 为等腰三角形． 5、