中考数学试题汇编——压轴题06 20页

(第 24 题图) (第 24 题备用图)       ,13 ,6636 ,6 ba cba c 2010 年中考数学试题分类汇编 压轴题(六) 24、（茂名市本题满分 8 分）如图，在直角坐标系 x O y 中，正方形 OCBA 的顶点 A、C 分别在 y 轴、 x 轴上， 点 B 坐标为（6，6），抛物线 cbxaxy  2 经过点 A、B 两点，且 13  ba ． （1）求 a ，b ， c 的值； （3 分） （2）如果动点 E、F 同时分别从点 A、点 B 出发，分别沿 A→B、B→C 运动，速度都是每秒 1 个单位长度，当点 E 到达终点 B 时，点 E、F 随之 停止运动．设运动时间为t 秒， EBF 的面积为 S． ①试求出 S 与 t 之间的函数关系式，并求出 S 的最大值； （2 分） ②当 S 取得最大值时，在抛物线上是否存在点 R，使得以 E、B、R、F 为顶点的四边形是平行四边形？如果存在，求出点 R 的坐标；如果不存 在，请说明理由． （ 3 分） 解：（1）由已知 A（0，6）、B（6，6）在抛物线上， 得方程组： ······1 分 解得： ·············3 分 （2）①运动开始t 秒时，EB＝ t6 ，BF＝t ， S＝ ttttBFEB 32 1)6(2 1 2 1 2  ，··········4 分 因为 2 9)3(2 132 1 22  tttS ， 所以当 3t 时，S 有最大值 2 9 ．··················5 分 ②当 S 取得最大值时，由①知 3t ，所以 BF＝3，CF＝3，EB＝6-3＝3． 若存在某点 R，使得以 E、B、R、F 为顶点的四边形是平行四边形， 则 EBFREBFR //11 且 ，即可得 R1 为（9，3）、（3，3）；··················6 分 或者 BFERBFER //22 且 ，可得 R2 为（3，9）．·························7 分 （第 25 题备用图） 再将所求得的三个点代入 63 2 9 1 2  xxy ，可知只有点（9，3）在抛物线上，因此抛物线上存在点 R1（9，3），使得四边形 EBRF 为平行四边形．············8 分 25、（茂名市本题满分 8 分）已知⊙O1 的半径为 R，周长为 C． （1）在⊙O1 内任意作三条弦，其长分别是 1l 、 2l 、 3l ．求证： 1l + 2l + 3l < C； （3 分） （2）如图，在直角坐标系 x O y 中，设⊙O1 的圆心为 O1 )( RR， ． ①当直线l ： )0(  bbxy 与⊙O1 相切时，求b 的值；（2 分） ②当反比例函数 )0(  kx ky 的图象与⊙O1 有两个交点时， 求 k 的取值范围． （3 分） 解： （1）证明： Rl 21  ， Rl 22  ， Rl 23  ． 1l + 2l + 3l CRR  223  ，2 分 因此， 1l + 2l + 3l < C．··········································3 分 （2）解：①如图，根据题意可知⊙O1 与与 x 轴、 y 轴分别相切，设直线l 与⊙O1 相切于点 M，则 O1M⊥l， 过点 O1 作直线 NH⊥ x 轴，与l 交于点 N，与 x 轴交于点 H，又∵直线l 与 x 轴、 y 轴分别交于点 E（ b ，0）、 F（0，b ），∴OE＝OF＝b ，∴∠NEO＝45o，∴∠ENO1＝45o，在 Rt△O1MN 中，O1N＝O1M  sin45o＝ R2 ， ∴点 N 的坐标为 N（R， RR 2 ），················4 分 把点 N 坐标代入 bxy  得： bRRR 2 ，解得： Rb 2 ，··········5 分 ②如图，设经过点 O、O1 的直线交⊙O1 于点 A、D，则由已知，直线 OO1： xy  是圆与反比例函数图象 的对称轴，当反比例函数 x ky  的图象与⊙O1 直径 AD 相交时（点 A、D 除外），则反比例函数 x ky  的图象与 ⊙O1 有两个交点． 过点 A 作 AB⊥ x 轴交 x 轴于点 B，过 O1 作 O1C⊥ x 轴于点 C，OO1＝O1C  sin45o＝ R2 ，OA＝ RR 2 ， 所以 OB＝AB＝ OA sin45o＝  2 2)2( RR RR 2 2 ， 因 此 点 A 的 坐 标 是 A )2 2,2 2( RRRR  ， 将 点 A 的 坐 标 代 入 x ky  ， 解 得 ： 2)22 3( Rk  ．·····································6 分 同理可求得点 D 的坐标为 D )2 2,2 2( RRRR  ， 将点 D 的坐标代入 x ky  ，解得： 2)22 3( Rk  ······7 分 所 以 当 反 比 例 函 数 )0(  kx ky 的 图 象 与 ⊙ O1 有 两 个 交 点 时 ， k 的 取 值 范 围 是 ： 22 )22 3()22 3( RkR  ······················· 8 分 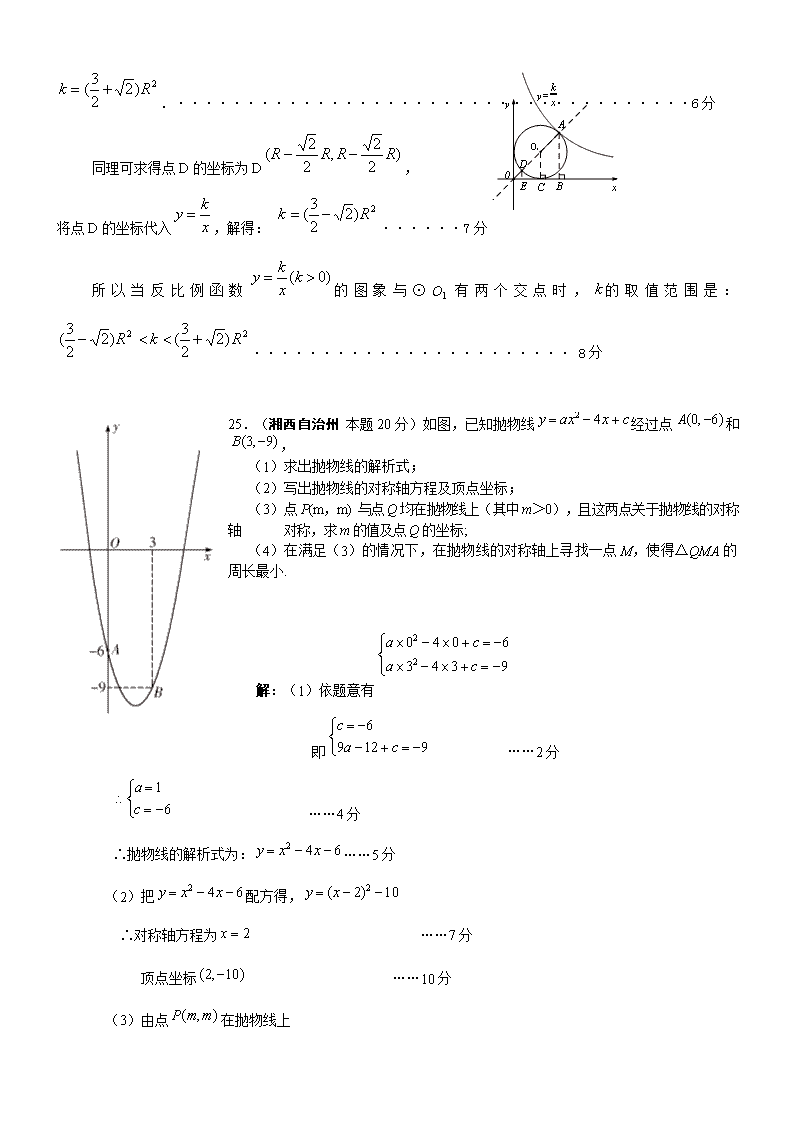25．（湘西自治州 本题 20 分）如图，已知抛物线 2 4y ax x c   经过点 (0, 6)A  和 (3, 9)B  ， （1）求出抛物线的解析式； （2）写出抛物线的对称轴方程及顶点坐标； （3）点 P(m，m) 与点 Q 均在抛物线上（其中 m＞0），且这两点关于抛物线的对称 轴 对称，求 m 的值及点 Q 的坐标; （4）在满足（3）的情况下，在抛物线的对称轴上寻找一点 M，使得△QMA 的 周长最小. 解：（1）依题意有 2 2 0 4 0 6 3 4 3 9 a c a c              即 6 9 12 9 c a c        ……2 分 1 6 a c    ……4 分 ∴抛物线的解析式为： 2 4 6y x x   ……5 分 （2）把 2 4 6y x x   配方得， 2( 2) 10y x   ∴对称轴方程为 2x  ……7 分 顶点坐标 (2, 10) ……10 分 （3）由点 ( , )P m m 在抛物线上 有 2 4 6m m m   ……12 分 即 2 5 6 0m m   ∴ 1 6m  或 2 1m   （舍去） ……13 分 ∴ (6,6)P ∵点 P 、 Q 均在抛物线上，且关于对称轴 2x  对称 ∴ ( 2,6)Q  ……15 分 （4）连接 ,AQ AP ，直线 AP 与对称轴 2x  相交于点 M 由于 ,P Q 两点关于对称轴对称，由轴对称性质可知，此时的交点 M ，能够使 得 △ QAM 的 周长最小. ……17 分 设直线 PA 的解析式 y kx b  ∴有 6 6 6 b k b       ∴ 2 6 k b     ∴直线 PA 的解析式为： 2 6y x  ……18 分 设点 (2, )M n 则有 2 2 6 2n      ……19 分 此时点 (2, 2)M  能够使得△ AMQ 的周长最小. ……20 分 26．（湘潭市 本题满分 10 分） 如图，直线 6y x   与 x 轴交于点 A，与 y 轴交于点 B，以线段 AB 为直径作⊙C，抛物线 cbxaxy  2 过 A、C、O 三点． (1) 求点 C 的坐标和抛物线的解析式； (2) 过点 B 作直线与 x 轴交于点 D，且 OB2=OA·OD，求证：DB 是⊙C 的切线； (3) 抛物线上是否存在一点 P， 使以 P、O、C、A 为顶点的四边形为直角梯形，如果存在，求出点 P 的坐 标；如果不存在，请说明理由． x y 解：（1）A（6，0），B（0，6） ……………………1 分 连结 OC,由于∠AOB=90 o，C 为 AB 的中点，则 ABOC 2 1 ， 所以点 O 在⊙C 上（没有说明不扣分）． 过 C 点作 CE⊥OA，垂足为 E，则 E 为 OA 中点,故点 C 的横坐标为 3． 又点 C 在直线 y=－x+6 上，故 C（3，3） ……………………2 分 抛物线过点 O，所以 c=0, 又抛物线过点 A、C，所以 3 9 3 0 36 6     a b a b ，解得： 1 , 23a b   所以抛物线解析式为 xxy 23 1 2  …………………3 分 （2）OA=OB=6 代入 OB2=OA·OD，得 OD=6 ……………………4 分 所以 OD=OB=OA，∠DBA=90o． ……………………5 分 又点 B 在圆上，故 DB 为⊙C 的切线 ……………………6 分 （通过证相似三角形得出亦可） （3）假设存在点 P 满足题意．因 C 为 AB 中点,O 在圆上,故∠OCA=90o, 要使以 P、O、C、A 为顶点的四边形为直角梯形， 则 ∠CAP=90o 或 ∠COP=90o, ……………………7 分 若∠CAP=90o,则 OC∥AP，因 OC 的方程为 y=x,设 AP 方程为 y=x+b． 又 AP 过点 A（6，0），则 b=－6, ……………………8 分 方程 y=x－6 与 xxy 23 1 2  联立解得： 1 1 6 0 x y   ， 2 2 3 9 x y   ， 故点 P1 坐标为（－3，－9） ……………………9 分 若∠COP=90o,则 OP∥AC，同理可求得点 P2（9，－9） (用抛物线的对称性求出亦可) 故存在点 P1 坐标为（－3，－9）和 P2（9，－9）满足题意．…………10 分 26 题图 28．(甘肃省 本小题满分 12 分)如图，抛物线与 x 轴交于 A（－1，0）、B（3，0）两点，与 y 轴交于点 C（0， －3），设抛物线的顶点为 D． （1）求该抛物线的解析式与顶点 D 的坐标； （2）以 B、C、D 为顶点的三角形是直角三角形吗？为什么？ （3）探究坐标轴上是否存在点 P，使得以 P、A、C 为顶点的三角形与△BCD 相似？若存在，请指出符合条件 的点 P 的位置，并直接写出点 P 的坐标；若不存在，请说明理由． 解： （1）设该抛物线的解析式为 cbxaxy  2 ， 由抛物线与 y 轴交于点 C（0，－3）,可知 3c . 即抛物线的解析式为 32  bxaxy ． ………………………1 分 把 A（－1，0）、B（3，0）代入, 得 3 0, 9 3 3 0. a b a b        解得 2,1  ba . ∴ 抛物线的解析式为 y = x2－2x－3． ……………………………………………3 分 ∴ 顶点 D 的坐标为  4,1  . ……………………………………………………4 分 说明：只要学生求对 2,1  ba ，不写“抛物线的解析式为 y = x2－2x－3”不扣分. （2）以 B、C、D 为顶点的三角形是直角三角形. ……………………………5 分 理由如下： 过点 D 分别作 x 轴、 y 轴的垂线，垂足分别为 E、F. 在 Rt△BOC 中，OB=3，OC=3，∴ 182 BC . …………………………6 分 在 Rt△CDF 中，DF=1，CF=OF-OC=4-3=1，∴ 22 CD . …………………………7 分 在 Rt△BDE 中，DE=4，BE=OB-OE=3-1=2，∴ 202 BD . …………………………8 分 ∴ 222 BDCDBC  ， 故△BCD 为直角三角形. …………………………9 分 （3）连接 AC，可知 Rt△COA∽ Rt△BCD，得符合条件的点为 O（0，0）． ………10 分 过 A 作 AP1⊥AC 交 y 轴正半轴于 P1，可知 Rt△CAP1 ∽ Rt△COA∽ Rt△BCD， 求得符合条件的点为 )3 1,0(1P ． …………………………………………11 分 过 C 作 CP2⊥AC 交 x 轴正半轴于 P2，可知 Rt△P2CA∽ Rt△COA∽ Rt△BCD， 求得符合条件的点为 P2（9，0）． …………………………………………12 分 ∴符合条件的点有三个：O（0，0）， )3 1,0(1P ，P2（9，0）. 26．（桂林市 本题满分 12 分）如图，过 A（8，0）、B（0，8 3 ）两点的直线与直线 xy 3 交于点 C．平 行于 y 轴的直线l 从原点 O 出发，以每秒 1 个单位长度的速度沿 x 轴向右平移，到 C 点时停止；l 分别交线 段 BC、OC 于点 D、E，以 DE 为边向左侧作等边△DEF，设△DEF 与△BCO 重叠部分的面积为 S（平方单 位），直线l 的运动时间为 t（秒）． （1）直接写出 C 点坐标和 t 的取值范围； （2）求 S 与 t 的函数关系式； （3）设直线l 与 x 轴交于点 P，是否存在这样的点 P，使得以 P、O、F 为顶点的三角形为等腰三角形，若存 在，请直接写出点 P 的坐标；若不存在，请说明理由． A 8 C O B 备用图1 8 3 y 3y x A 8P C E O D F B l 3y x y 8 3 解（1）C（4， 4 3 ） ……………………………2 分 t 的取值范围是：0≤t ≤4 ……………………………… 3 分 （2）∵D 点的坐标是（t ， 3 8 3t  ），E 的坐标是（t ， 3t ） ∴DE= 3 8 3t  - 3t =8 3 2 3t ……………………4 分 ∴等边△DEF 的 DE 边上的高为：12 3t ∴当点 F 在 BO 边上时：12 3t =t ，∴t =3 ……………………5 分 当 0≤t <3 时，重叠部分为等腰梯形，可求梯形上底为：8 3 2 3t - 2 3 3 t …7 分 S= 2 3(8 3 2 3 8 3 2 3 )2 3 t t t t    = 14(16 3 3 )2 3 t t = 27 3 8 33 t t  ………………………………8 分 当 3≤t ≤4 时，重叠部分为等边三角形 S= 1 (8 3 2 3 )(12 3 )2 t t  ………………… 9 分 = 23 3 24 3 48 3t t  ……………………10 分 （3）存在，P（ 24 7 ，0） ……………………12 分 说明：∵FO≥ 4 3 ，FP≥ 4 3 ，OP≤4 ∴以 P，O，F 以顶点的等腰三角形，腰只有可能是 FO，FP, 若 FO=FP 时， t =2（12-3t ），t = 24 7 ，∴P（ 24 7 ，0） A 8P C E O D F B l 3y x x y 8 3 30. (江西省南昌市) 课题：两个重叠的正多边形，其中的一个绕某一个顶点旋转所形成的有关问题． 实验与论证 设旋转角∠A1A0B1＝α（α＜∠A1A0B1），θ1，θ2，θ3，θ4，θ5，θ6 所表示的角如图所示． （1）用含α的式子表示：θ3＝_________，θ4＝_________，θ5＝_________； （2）图 1－图 4 中，连接 A0H 时，在不添加其他辅助线的情况下，是否存在与直线 A0H 垂直且被它平分的线 段？若存在，请选择期中的一个图给出证明；若不存在，请说明理由； 归纳与猜想 设正 n 边形 A0A1A2…An-1 与正 n 边形 A0B1B2…Bn-1 重合（其中，A1 与 B1 重合），现将正 n 边形 A0B1B2…Bn-1 绕顶点 A0 逆时针旋转α（ n  1800   ）． （3）设θn 与上述“θ3，θ4，…”的意义一样，请直接写出θn 的度数； （4）试猜想在正 n 边形且不添加其他辅助线的情形下，是否存在与直线 A0H 垂直且被它平分的线段？若存 在，请将这条线段用相应的顶点字母表示出来（不要求证明）；若不存在，请说明理由． 解：（1） 60 ，  ， 36 .······················································ 3 分 说明：每写对一个给 1 分. （2）存在.下面就所选图形的不同分别给出证明： 选图 1.图 1 中有直线 HAo 垂直平分 12 BA ，证明如下： 图 1 方法一： 证明：∵ 21 AAAo 与 210 BBA 是全等的等边三角形， ∴ 1020 BAAA  ， ∴ 210120 ABABAA  . 又∵  601020 HBAHAA . ∴ 2112 AHBBHA  . ∴ HBHA 12  .∴点 H 在线段 12 BA 的垂直平分线上. 又∵ 1020 BAAA  ，∴点 0A 在线段 12 BA 的垂直平分线上 ∴直线 HAo 垂直平分 12 BA ····················································· 8 分 方法二： 证明：∵ 21 AAAo 与 210 BBA 是全等的等边三角形， ∴ 1020 BAAA  ， ∴ 210120 ABABAA  . 又 HBAHAA 1020  . ∴ 2112 ABHBHA  ∴ 12 HBHA  . 在 HAA 20 与 HBA 10 中 ∵ 1020 BAAA  ， 12 HBHA  ， HBAHAA 1020  ∴ HAA 20 ≌ HBA 10 .∴ HABHAA 0102  ∴ HAo 是等腰三角形 102 BAA 的顶角平分线. ∴直线 HAo 垂直平分 12 BA . ·················································· 8 分 选图 2.图 2 中有直线 HAo 垂直平分 22 BA ，证明如下： 图 2 ∵ 2020 AABA  ∴ 220220 BAAABA  又∵  45320120 AAABBA ， ∴ 2222 BHAAHB  . ∴ 22 HAHB  .∴点 H 在线段 22 BA 的垂直平分线上. 又∵ 2020 AABA  ，∴点 0A 在线段 22 BA 的垂直平分线上 ∴直线 HAo 垂直平分 22 BA . ···································································· 8 分 说明：（ⅰ）在图 2 中选用方法二证明的，参照上面的方法二给分； （ⅱ）选择图 3 或图 4 给予证明的，参照上述证明过程评分. (3)当 n为奇数时，    nn 180 ， 当 n为偶数时，  n ···························································· 10 分 （4）存在.当 n为奇数时，直线 HAo 垂直平分 2 1 2 1  nn BA ， 当 n为偶数时，直线 HAo 垂直平分 22 nn BA .·································· 12 分 26．（山东省泰安市 本小题满分 10 分） 如图，△ABC 是等腰三角形，AB=AC，以 AC 为直径的⊙O 与 BC 交于点 D，DE⊥AB，垂足为 E，ED 的 延长线与 AC 的延长线交于点 F。 （1）求证：DE 是⊙O 的切线； （2）若⊙O 的半径为 2，BE=1，求 cosA 的值. 解：（1）证明：连结 AD、OD ∵AC 是直径 ∴AD⊥BC （2 分） ∵AB=AC ∴D 是 BC 的中点 又∵O 是 AC 的中点 ∴OD//AB （4 分） ∵DE⊥AB ∴OD⊥DE ∴DE 是⊙O 的切线 （6 分） （2）由（1）知 OD//AE ∴ AE OD FA FO  （8 分） ∴ BEAB OD ACFC OCFC   ∴ 14 2 4 2   FC FC 解得 FC=2 ∴AF=6 ∴cosA= 2 1 6 14  AF BEAB AF AE （10 分） 23．（深圳市本题 9 分）如图 10，以点 M（－1,0）为圆心的圆与 y 轴、x 轴分别交于点 A、B、C、D，直线 y＝ － 3 3 x－ 5 3 3 与⊙M 相切于点 H，交 x 轴于点 E，交 y 轴于点 F． （1）请直接写出 OE、⊙M 的半径 r、CH 的长；（3 分） （2）如图 11，弦 HQ 交 x 轴于点 P，且 DP:PH＝3:2，求 cos∠QHC 的值；（3 分） （3）如图 12，点 K 为线段 EC 上一动点（不与 E、C 重合），连接 BK 交⊙M 于点 T，弦 AT 交 x 轴于点 N．是 否存在一个常数 a，始终满足 MN·MK＝a，如果存在，请求出 a 的值；如果不存在，请说明理由．（3 分） 解： （1）、如图 4，OE=5， 2r  ，CH=2 （2）、如图 5，连接 QC、QD，则 90CQD   ， QHC QDC   易知 CHP DQP : ，故 DP DQ PH CH  ， 3 2 2 DQ ， 3DQ  ，由于 4CD  ， 3cos cos 4 QDQHC QDC CD       ； （3）、如图 6，连接 AK，AM，延长 AM， 与圆交于点 G，连接 TG，则 90GTA   2 4 90     3 4   ， 2 3 90    由于 3 90BKO    ，故， 2BKO   ； 而 1BKO   ，故 1 2   图 5 F F 图 6 1 xD A B H CE M O F 图 10 x y D A B H CE M O 图 11 P Q x y D A B H CE M O F 图 12 N K y F 图 4 在 AMK 和 NMA 中， 1 2   ； AMK NMA   故 AMK NMA : ； MN AM AM MK  ; 即： 2 4MN MK AM g 故存在常数 a ，始终满足 MN MK ag 常数 4a  25、（天津市 本小题 10 分） 在平面直角坐标系中，矩形 OACB 的顶点 O 在坐标原点，顶点 A、B 分别在 x 轴、 y 轴的正半轴上， 3OA  ， 4OB  ，D 为边 OB 的中点. （Ⅰ）若 E 为边 OA 上的一个动点，当△ CDE 的周长最小时，求点 E 的坐标； （Ⅱ）若 E 、 F 为边 OA 上的两个动点，且 2EF  ，当四边形CDEF 的周长最小时，求点 E 、 F 的坐标. 第（25）题 y B O D C A xE D y B O D C A x 温馨提示：如图，可以作点 D 关于 x 轴 的对称点 D ，连接 CD 与 x 轴交于 点 E，此时△ CDE 的周长是最小的.这样， 解：（Ⅰ）如图，作点 D 关于 x 轴的对称点 D，连接 CD 与 x 轴交于点 E，连接 DE . 若在边 OA 上任取点 E （与点 E 不重合），连接 CE 、 DE 、 D E  . 由 DE CE D E CE CD D E CE DE CE              ， 可知△ CDE 的周长最小. ∵ 在矩形OACB 中， 3OA  ， 4OB  ， D 为OB 的中点， ∴ 3BC  ， 2D O DO   ， 6D B  . ∵ OE∥BC， ∴ Rt△ D OE ∽Rt△ D BC ，有 OE D O BC D B   . ∴ 2 3 16 D O BCOE D B      . ∴ 点 E 的坐标为（1，0）. ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6 分 （Ⅱ）如图，作点 D 关于 x 轴的对称点 D，在 CB 边上截取 2CG  ，连接 D G 与 x 轴交于点 E ，在 EA 上截 取 2EF  . ∵ GC∥EF， GC EF ， ∴ 四边形GEFC 为平行四边形，有 GE CF . 又 DC 、 EF 的长为定值， ∴ 此时得到的点 E 、 F 使四边形 CDEF 的周长最小. ∵ OE∥BC， ∴ Rt△ D OE ∽Rt△ D BG , 有 OE D O BG D B   . ∴ ( ) 2 1 1 6 3 D O BG D O BC CGOE D B D B          . ∴ 1 723 3OF OE EF     . ∴ 点 E 的坐标为（ 1 3 ，0），点 F 的坐标为（ 7 3 ，0）. ．．．．．．．．．．．．．．．10 分 26、（天津市 本小题 10 分） 在平面直角坐标系中，已知抛物线 2y x bx c    与 x 轴交于点 A 、 B （点 A 在点 B 的左侧），与 y 轴的正 半轴交于点 C ，顶点为 E . y B O D C A xE D G F y B O D C A xE E D （Ⅰ）若 2b  ， 3c  ，求此时抛物线顶点 E 的坐标； （Ⅱ）将（Ⅰ ） 中 的抛 物 线 向 下 平移 ， 若 平 移 后， 在 四 边 形 ABEC 中 满 足 S△BCE = S△ABC，求此时直线 BC 的解析式； （ Ⅲ ） 将 （ Ⅰ ） 中 的 抛 物 线 作 适 当 的 平 移 ， 若 平 移 后 ， 在 四 边 形 A B E C 中 满 足 S△BCE = 2S△AOC，且顶点 E 恰好落在直线 4 3y x   上，求此时抛物线的解析式. 解：（Ⅰ）当 2b  ， 3c  时，抛物线的解析式为 2 2 3y x x    ，即 2( 1) 4y x    . ∴ 抛物线顶点 E 的坐标为（1，4）． ．．．．．．．．．．．．．．．．．2 分 （Ⅱ）将（Ⅰ）中的抛物线向下平移，则顶点 E 在对称轴 1x  上，有 2b  ， ∴ 抛物线的解析式为 2 2y x x c    （ 0c  ）． ∴ 此时，抛物线与 y 轴的交点为 0( )C c， ，顶点为 1( 1 )E c， ． ∵ 方程 2 2 0x x c    的两个根为 1 1 1x c   ， 2 1 1x c   ， ∴ 此时，抛物线与 x 轴的交点为 1 1 0( )A c  ， ， 1 1 0( )B c  ， ． 如图，过点 E 作 EF∥CB 与 x 轴交于点 F ，连接 CF ，则 S△BCE = S△BCF． ∵ S△BCE = S△ABC， ∴ S△BCF = S△ABC． ∴ 2 1BF AB c   ． 设对称轴 1x  与 x 轴交于点 D ， 则 1 3 12DF AB BF c    ． 由 EF∥CB，得 EFD CBO   ． ∴ Rt△EDF∽Rt△COB．有 ED CO DF OB  ． ∴ 1 3 1 1 1 c c c c      ．结合题意，解得 5 4c  ． ∴ 点 5 4 (0 )C ， ， 5 2 ( 0)B ， ． 26.( 大连市)如图 17，抛物线 F： 2 ( 0)y ax bx c a    与 y 轴相交于点 C，直线 1L 经过点 C 且平行于 x 轴， E y xFBDA O C 1x  将 1L 向上平移 t 个单位得到直线 2L ，设 1L 与抛物线 F 的交点为 C、D， 2L 与抛物线 F 的交点为 A、B，连接 AC、 BC （1）当 1 2a  ， 3 2b   ， 1c  ， 2t  时，探究△ABC 的形状，并说明理由； （2）若△ABC 为直角三角形，求 t 的值（用含 a 的式子表示）； （3）在（2）的条件下，若点 A 关于 y 轴的对称点 A’恰好在抛物线 F 的对称轴上，连接 A’C，BD，求四边形 A’CDB 的面积（用含 a 的式子表示） 2L O C A B D x 图 17 1L 解：（1）结论： ABC△ 是直角三角形.··························································1 分 由题意： 21 3 12 2y x x   令 21 3 1 32 2x x   解得 1 21 4x x  ， 点 A B、 的坐标分别为 ( 13) (4 3)A B ，、 ， 设 2l 与 y 轴相交于点 P ，在 Rt ACP△ 和 Rt BCP△ 中 2 2 5AC AP CP   2 2 2 2 2 20 4 ( 1) 5 BC BP CP AB AC BC AB           ABC△ 是直角三角形··············································································· 2 分 （2）由题意， 90ACB   ，设点 B 的坐标为 ( )m c t， 2c t am bm c     ················································································ 3 分 2t am bm   ························································································· 4 分 设 E 为 AB 的中点，则点 E 的坐标为 2 b c ta      ， ABC△ 为直角三角形 EC EB  ······························································································ 5 分 即 2 2 2 2 b bt ma a               ····································································6 分 2 2at am bm t    ················································································· 7 分 1 2 1 0t ta   ， （舍去）············································································8 分 （3）依题意，点 A与点 E 重合 A 在抛物线 F 的对称轴上， A 与 A关于 y 轴对称 2 2 2 b bA B AA PA a a              CD x ∥ 轴 2 2 2 b bCD PA A Ba a             A B CD ∥ 四边形 A CDB 是平行四边形·····································································9 分 在 Rt ABC△ 中 A C AA  A 与 A关于 y 轴对称 AC A C AA    ACA△ 为等边三角形············································································· 10 分 22 32 2( 30 ) 3A CDBS A B CP PA CP t t t        · · ·tan · ······························11 分 2 2 3 3a  ··································································································· 12 分 设直线 BC 的解析式为 y mx n  ，则 5 ,4 50 .2 n m n      解得 1 ,2 5.4 m n      ∴ 直线 BC 的解析式为 1 5 2 4y x   . ．．．．．．．．．．．．．．．．．．．．．．．．．6 分 （Ⅲ）根据题意，设抛物线的顶点为 ( )E h k， ，（ 0h  ， 0k  ） 则抛物线的解析式为 2( )y x h k    ， 此时，抛物线与 y 轴的交点为 2(0 )C h k ， ， 与 x 轴的交点为 0( )A h k ， ， 0( )B h k ， .（ 0k h  ） 过点 E 作 EF∥CB 与 x 轴交于点 F ，连接 CF ， 则 S△BCE = S△BCF. 由 S△BCE = 2S△AOC， ∴ S△BCF = 2S△AOC. 得 2 2( )BF AO k h   . 设该抛物线的对称轴与 x 轴交于点 D . 则 1 3 22DF AB BF k h    . 于是，由 Rt△EDF∽Rt△COB，有 ED CO DF OB  ． ∴ 2 3 2 k h k k h h k     ，即 22 5 2 0h kh k   ． 结合题意，解得 1 2h k ． ① ∵ 点 ( )E h k， 在直线 4 3y x   上，有 4 3k h   ． ② ∴ 由①②，结合题意，解得 1k  ． 有 1k  ， 1 2h  ． ∴ 抛物线的解析式为 2 3 4y x x    ． ．．．．．．．．．．．．．．．．．．．．．．．．．10 分 28．(徐州市 本题 10 分)如图，已知二次函数 y= 42 3 4 1 2  xx 的图象与 y 轴交于点 A，与 x 轴交于 B、C 两点， 其对称轴与 x 轴交于点 D，连接 AC． (1)点 A 的坐标为_______ ，点 C 的坐标为_______ ； (2)线段 AC 上是否存在点 E，使得△EDC 为等腰三角形?若存在，求出所有符合条件的点 E 的坐标；若不存在， 请说明理由； (3)点 P 为 x 轴上方的抛物线上的一个动点，连接 PA、PC，若所得△PAC 的面积为 S，则 S 取何值时，相应的 点 P 有且只有 2 个?