中考解直角三角形知识点整理复习 9页

中考解直角三角形 考点一、直角三角形的性质 ‎ ‎1、直角三角形的两个锐角互余：可表示如下：∠C=90°∠A+∠B=90°‎ ‎2、在直角三角形中，30°角所对的直角边等于斜边的一半。‎ ‎3、直角三角形斜边上的中线等于斜边的一半 ‎4、勾股定理： 如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2. 即直角三角形两直角边的平方和等于斜边的平方 勾：直角三角形较短的直角边 股：直角三角形较长的直角边 弦：斜边 勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a2＋b2＝c2，那么这个三角形是直角三角形。‎ 考点二、直角三角形的判定 ‎1、有一个角是直角的三角形是直角三角形、有两个角互余的三角形是直角三角形 ‎2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。‎ ‎3、勾股定理的逆定理：如果三角形的三边长a、b、c满足a2+b2=c2 ，那么这个三角形是直角三角形。（经典直角三角形：勾三、股四、弦五）‎ 用它判断三角形是否为直角三角形的一般步骤是：‎ ‎（1）确定最大边（不妨设为c）；‎ ‎（2）若c2＝a2＋b2，则△ABC是以∠C为直角的三角形；‎ 若a2＋b2＜c2，则此三角形为钝角三角形（其中c为最大边）；‎ 若a2＋b2＞c2，则此三角形为锐角三角形（其中c为最大边）‎ ‎4. 勾股定理的作用：‎ ‎ （1）已知直角三角形的两边求第三边。‎ ‎ （2）已知直角三角形的一边，求另两边的关系。‎ ‎（3）用于证明线段平方关系的问题。‎ ‎（4）利用勾股定理，作出长为的线段 考点三、锐角三角函数的概念 ‎ ‎1、如图，在△ABC中，∠C=90° ‎ ‎①锐角A的对边与斜边的比叫做∠A的正弦，记为sinA，即 ‎②锐角A的邻边与斜边的比叫做∠A的余弦，记为cosA，即 ‎③锐角A的对边与邻边的比叫做∠A的正切，记为tanA，即 ‎④锐角A的邻边与对边的比叫做∠A的余切，记为cotA，即 ‎2、锐角三角函数的概念 锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数 ‎3、一些特殊角的三角函数值 三角函数 ‎ 30°‎ ‎ 45°‎ ‎ 60°‎ sinα cosα tanα ‎1‎ cotα ‎1‎ ‎4、各锐角三角函数之间的关系 ‎（1）互余关系：sinA=cos(90°—A)，cosA=sin(90°—A) ；‎ ‎（2）平方关系：‎ ‎（3）倒数关系：tanAtan(90°—A)=1‎ ‎（4）商（弦切）关系：tanA=‎ ‎5、锐角三角函数的增减性 当角度在0°~90°之间变化时，‎ ‎（1）正弦值随着角度的增大（或减小）而增大（或减小）；（2）余弦值随着角度的增大（或减小）而减小（或增大）；（3）正切值随着角度的增大（或减小）而增大（或减小）；（4）余切值随着角度的增大（或减小）而减小（或增大）‎ 考点四、解直角三角形 ‎ ‎1、解直角三角形的概念 在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。‎ ‎2、解直角三角形的理论依据 在Rt△ABC中，∠C=90°，∠A，∠B，∠C所对的边分别为a，b，c ‎（1）三边之间的关系：（勾股定理）‎ ‎（2）锐角之间的关系：∠A+∠B=90°‎ ‎（3）边角之间的关系：正弦sin，余弦cos，正切tan ‎(4) 面积公式： （hc为c边上的高）‎ 考点五、解直角三角形 应用 ‎1、将实际问题转化到直角三角形中，用锐角三角函数、代数和几何知识综合求解 ‎2、仰角、俯角、坡面 知识点及应用举例：‎ ‎(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。‎ ‎ ‎ ‎(2)坡面的铅直高度和水平宽度的比叫做坡度(坡比)。用字母表示，即。坡度一般写成的形式，如等。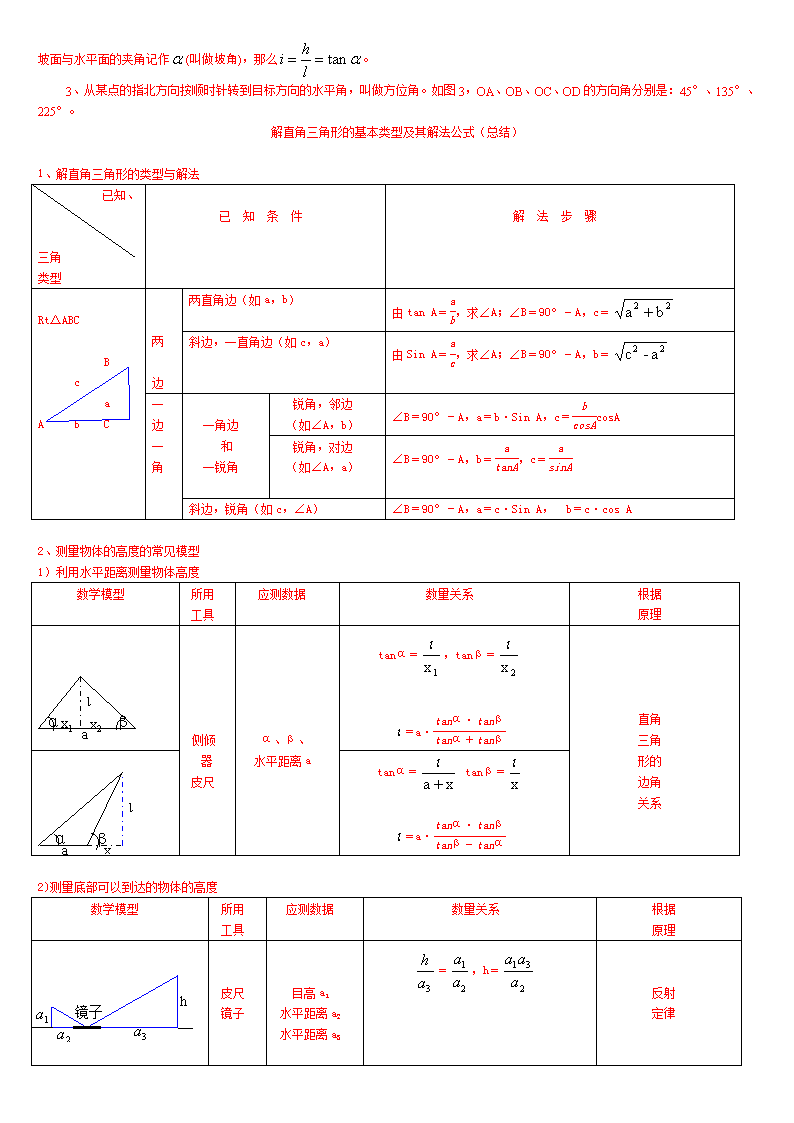 ‎ ‎ 把坡面与水平面的夹角记作(叫做坡角)，那么。‎ ‎3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。如图3，OA、OB、OC、OD的方向角分别是：45°、135°、225°。‎ 解直角三角形的基本类型及其解法公式（总结）‎ ‎1、解直角三角形的类型与解法 ‎ 已知、解法 三角 ‎ 类型 已 知 条 件 解 法 步 骤 ‎ ‎ Rt△ABC ‎ B ‎ c ‎ a A b C ‎ ‎ ‎ ‎ 两 边 两直角边（如a，b）‎ 由tan A＝，求∠A；∠B＝90°－A，c＝‎ 斜边，一直角边（如c，a）‎ 由Sin A＝，求∠A；∠B＝90°－A，b＝‎ 一 边 一 角 一角边 和 一锐角 锐角，邻边 ‎（如∠A，b）‎ ‎∠B＝90°－A，a＝b·Sin A，c＝cosA 锐角，对边 ‎（如∠A，a）‎ ‎∠B＝90°－A，b＝，c＝ 斜边，锐角（如c，∠A）‎ ‎∠B＝90°－A，a＝c·Sin A， b＝c·cos A ‎2、测量物体的高度的常见模型 ‎1）利用水平距离测量物体高度 数学模型 所用工具 应测数据 数量关系 根据 原理 ι x2‎ x1‎ a α β 侧倾器 皮尺 α、β、‎ 水平距离a tanα＝，tanβ＝‎ ‎＝a· 直角 三角 形的 边角 关系 ι a x β α tanα＝ tanβ＝‎ ‎＝a· ‎2)测量底部可以到达的物体的高度 数学模型 所用工具 应测数据 数量关系 根据 原理 h 镜子 皮尺 镜子 目高a1‎ 水平距离a2‎ 水平距离a3‎ ‎＝，h＝‎ 反射 定律 h 皮尺 标杆 标杆高a1‎ 标杆影长a2‎ 物体影长a3‎ ‎＝,h＝‎ 同一时刻物高与影长成正比 h α 皮尺 侧倾器 侧倾器高a1‎ 水平距离a2‎ 倾斜角α tanα＝,‎ h＝a1＋a2tanα 矩形的性质和直角三角形的边角关系 α β α h 仰角α 俯角β 水平距离a1‎ tanα＝, tanβ＝‎ h＝h1＋h2＝a1（tanα＋tanβ）‎ 矩形的性质和直角三角形的边角关系 ‎3）测量底部不可到达的物体的高度（1）‎ 数学模型 所用工具 应测数据 数量关系 根据 理论 x β α h 皮尺 侧倾器 仰角α 俯角β 高度a tanα＝ ，tanβ＝‎ h＝a＋h1＝a＋a＝a(1＋)‎ 矩形的性质和直角三角形的边角关系 β α a x h 俯角α 俯角β 高度 tanα＝, tanβ＝‎ ‎∴x＝＝ ∴h＝a－ 测量底部不可到达的物体的高度（2）‎ 数字模型 所用工具 应测距离 数量关系 根据 原理 β A α x h 仰角α，‎ 仰角β 水平距离a1‎ tanα＝ tanβ＝‎ ‎∴h1＝‎ 皮尺侧倾器 侧倾器高a2‎ h＝a2＋h1＝a2＋‎ 矩形的性质和直角三角形的边角关系 β α x a h 仰角α 仰角β 高度a tanα＝, tanβ＝ h＝ tanα＝, tanβ＝、h＝ β α x a h 仰角α 仰角β 高度a tanα＝, tanβ＝ h＝ 第三部分 真题分类汇编详解2007-2012‎ ‎（2007）19．（本小题满分6分）一艘轮船自西向东航行，在A处测得东偏北21.3°方向有一座小岛C，继续向东航行60海里到达B处，测得小岛C此时在轮船的东偏北63.5°方向上．之后，轮船继续向东航行多少海里，距离小岛C最近？（参考数据：sin21.3°≈，tan21.3°≈， sin63.5°≈，tan63.5°≈2）‎ ‎（2008）19．（本小题满分6分）在一次课题学习课上，同学们为教室窗户设计一个遮阳蓬，小明同学绘制的设计图如图所示，其中，表示窗户，且米，表示直角遮阳蓬，已知当地一年中在午时的太阳光与水平线的最小夹角为，最大夹角为．请你根据以上数据，帮助小明同学计算出遮阳蓬中的长是多少米？（结果保留两个有效数字）‎ C G E D B A F 第19题图 A Ｄ Ｃ B Ｄ ‎（参考数据：，，，）‎ ‎（2009）19．（本小题满分6分）在一次数学活动课上，老师带领同学们去测量一座古塔CD的高度．他们首先从A处安置测倾器，测得塔顶C的仰角，然后往塔的方向前进50米到达B处，此时测得仰角，已知测倾器高1.5米，请你根据以上数据计算出古塔CD的高度．‎ ‎（参考数据：，，，）‎ A ‎（2010）19．（本小题满分6分）小明家所在居民楼的对面有一座大厦AB，AB＝米．为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）‎ ‎（参考数据：）‎ 解：‎ D ‎37°‎ C ‎48°‎ B ‎ ‎ 第19题图 ‎40º ‎35º A D B C ‎（2011）19．(6分)某商场准备改善原有楼梯的安全性能，把倾斜角由 原来的40º减至35º．已知原楼梯AB长为5m，调整后的楼梯所占地 面CD有多长？‎ ‎(结果精确到0.1m．参考数据：sin40º≈0.64，cos40º≈0.77，sin35º≈0.57，tan35º≈0.70)‎ ‎（2012）20.（8分）‎ 附历年真题标准答案：‎ ‎（2007）19．（本小题满分6分）‎ B C D A 解：过C作AB的垂线，交直线AB于点D，得到Rt△ACD与Rt△BCD．‎ 设BD＝x海里，‎ 在Rt△BCD中，tan∠CBD＝，∴CD＝x ·tan63.5°．‎ 在Rt△ACD中，AD＝AB＋BD＝(60＋x)海里，tan∠A＝，‎ ‎∴CD＝( 60＋x ) ·tan21.3°． ∴x·tan63.5°＝(60＋x)·tan21.3°，即 ．解得，x＝15．‎ 答：轮船继续向东航行15海里，距离小岛C最近． …………………………6′‎ ‎（2008）19．（本小题满分6分）‎ 解：设CD为x ，在Rt△BCD中，， ‎ ‎∵，∴． 2′‎ C G E D B A F 第19题图 在Rt△ACD中，， ∵，∴． ‎ ‎∵，∴． ．‎ 答：CD长约为1.14米． 　 ‎ ‎（2009）19．（本小题满分6分）‎ 解：由题意知，，‎ ‎∴，设，‎ 在中，，则；‎ 在中，，则 ‎∵，∴． ，∴（米）．‎ 答：古塔的高度约是39米． 6分 B ‎37°‎ ‎48°‎ D C A 第19题图 ‎（2010）19．（本小题满分6分）‎ 解：设CD = x．在Rt△ACD中，，‎ 则，∴.‎ 在Rt△BCD中，tan48° = ，‎ 则，‎ ‎∴. ……………………4分 ‎∵AD＋BD = AB，∴．‎ 解得：x≈43．‎ 答：小明家所在居民楼与大厦的距离CD大约是43米． ………………… 6分 ‎（2011）19．（本小题满分6分）‎ ‎（2012）20.（8分）‎ 谢谢