中考数学易错题 4页

‎1.反比例函数：一般地，形如：（k为常数，k≠0）的函数称为反比例函数，其中x 是自变量，y 是x的函数，k是反比例系数．‎ 反比例函数有三种表示形式： 、 、 ‎ ‎2.反比例函数图象及画法：一般地，反比例函数（为常数，≠0）的图象是由两个分支组成的，是双曲线．这两个分支分别位于第一、三象限或第二、四象限．‎ 双曲线两个分支关于原点对称，由于反比例函数中，自变量x≠0，函数值y≠0，所以它的图象与 x轴和y轴都没有交点，即双曲线的两个分支无限地接近坐标轴，但永远不与坐标轴相交．‎ 反比例函数图象既是以直线 和直线 为对称轴的轴对称图形；又是是以 为对称中心的中心对称图形。过原点任意画一条直线，与两个分支交于两点，则这两个交点是关于 对称的，即若一个交点是，则另一个交点是 ．‎ 画反比例函数的图象的基本步骤为： ① 列表；描点；③ 连线．‎ ‎3.反比例函数性质：‎ ‎（1）反比例函数图象的位置和函数值的增减性都是由比例系数k来确定的： ‎ ‎① 当 k＞0时， x，y 同号，图象在第一、三象限，在每一个象限内，‎ 由左至右呈下降趋势，y 随x的增大而减小； ‎ ‎② 当 k＜0时， x，y 异号，图象在第二、四象限，在每一个象限内，‎ 由左向右呈上升趋势，y 随x的增大而增大． ‎ ‎（2）描述函数值的增减情况时，必须指出“在同一象限内”，‎ 否则，若笼统地说：“当k＞0时，y 随x的增大而减小”，就会出现与事实不符的错误，‎ 如函数，当x时，y；当 x=2 时，y=3 ．显然不是y随x的增大而减小．‎ ‎4.求反比例函数关系式的基本方法,是待定系数法。‎ 过反比例函数图象上的任意一点作 x 轴的垂线，那么这点与垂足、坐标系原点构成的三角形的面积是一个定值，即。过反比例函数图象上的任意一点作 x 轴、Y 轴的垂线，那么这点与坐标轴构成的矩形的面积是一个定值，即 ‎【例1】当m取什么值时，函数是反比例函数？‎ ‎【例2】已知函数y＝y1＋y2，y1与x成正比例，y2与x成反比例，且当x＝1时，y＝4；当x＝2时，y＝5．‎ ‎（1）求y与x的函数关系式；‎ ‎（2）当x＝－2时，求函数y的值．‎ ‎【例3】下列函数中，是反比例函数的是 （ ）‎ ‎ A． B． C． D．‎ ‎【例4】若y与－2x成反比例函数关系，x与成正比例，则y与z的关系 （ ）‎ A．成正比例函数 B．成反比例函数 C．成一次函数 D．不能确定 ‎【例5】面积为8的△ABC，一边长x，这边上的高为y，则y与x的变化规律用图象表示大致是 （ ）‎ ‎ A． B． C． D．‎ ‎【例6】已知点（2，5）在反比例函数y=的图象上，则下列各点在该函数图象上的是（ ）‎ A．（2，—5） B．（—5，—2） ‎ C．（—3，4） D．（4，—3）‎ ‎【例7】在同一直角坐标平面内，如果直线与反比例函数的图象没有交点，那么和的关系一定是（ ）‎ A <0，>0 B >0，<0‎ ‎ C 、同号 D 、异号 ‎【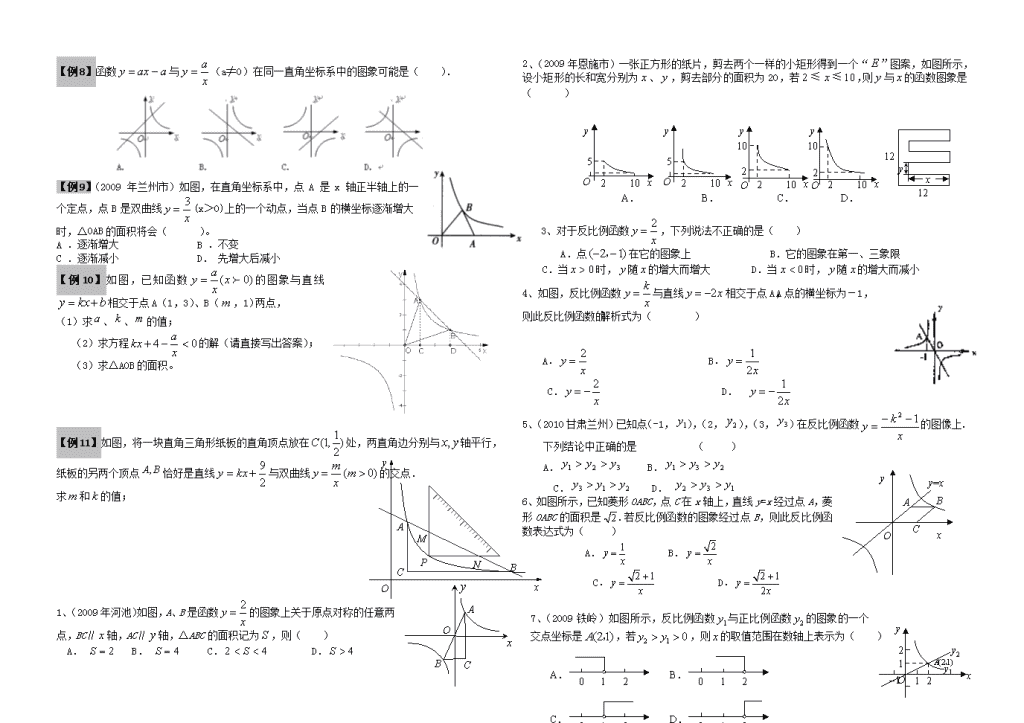例8】函数与（a≠0）在同一直角坐标系中的图象可能是（ ）．‎ ‎【例9】（2009 年兰州市）如图，在直角坐标系中，点 A 是 x 轴正半轴上的一个定点，点 B 是双曲线(x＞0)上的一个动点，当点 B 的横坐标逐渐增大时，△OAB的面积将会（ ）。‎ A ．逐渐增大 B ．不变 C ．逐渐减小 D． 先增大后减小 ‎【例10】如图，已知函数的图象与直线相交于点A（1，3）、B（，1）两点，‎ ‎（1）求、、的值；‎ ‎（2）求方程的解（请直接写出答案）；‎ ‎（3）求△AOB的面积。‎ y ‎ x ‎ O N M C ‎ A ‎ B P ‎【例11】如图，将一块直角三角形纸板的直角顶点放在处，两直角边分别与轴平行，纸板的另两个顶点恰好是直线与双曲线的交点．‎ 求和的值；‎ O B C A ‎1、（2009年河池）如图，A、B是函数的图象上关于原点对称的任意两点，BC∥轴，AC∥轴，△ABC的面积记为，则（ ）‎ ‎ A． B． C． D．‎ ‎2、（2009年恩施市）一张正方形的纸片，剪去两个一样的小矩形得到一个“”图案，如图所示，设小矩形的长和宽分别为、，剪去部分的面积为20，若，则与的函数图象是（　　　）‎ ‎2‎ ‎10‎ ‎5‎ O x y ‎2‎ ‎10‎ ‎5‎ O x y ‎2‎ ‎10‎ ‎10‎ O x y ‎2‎ ‎10‎ ‎10‎ O x y y x ‎12‎ ‎2‎ ‎2‎ A． 　　 B． 　 C． D．‎ ‎12‎ ‎3、对于反比例函数，下列说法不正确的是（ ）‎ A．点在它的图象上 B．它的图象在第一、三象限 C．当时，随的增大而增大 D．当时，随的增大而减小 ‎4、如图，反比例函数与直线相交于点A，A点的横坐标为－1，则此反比例函数的解析式为（　　　　）‎ A．　　　　 B．　　　‎ C．　　　　　 D．　‎ ‎5、（2010甘肃兰州）已知点（-1，），（2，），（3，）在反比例函数的图像上. 下列结论中正确的是 （ ）‎ ‎ A． B． ‎O A B C x y y=x ‎ C． D． ‎ ‎6、如图所示，已知菱形OABC，点C在x轴上，直线y=x经过点A，菱形OABC的面积是.若反比例函数的图象经过点B，则此反比例函数表达式为（ ）‎ A． B． ‎ C． D．‎ ‎7、（2009铁岭）如图所示，反比例函数与正比例函数的图象的一个交点坐标是，若，则的取值范围在数轴上表示为（ ）‎ y ‎1‎ ‎2‎ ‎2‎ ‎1‎ y2‎ y1‎ x O ‎1‎ ‎2‎ ‎0‎ A．‎ ‎1‎ ‎2‎ ‎0‎ B．‎ ‎1‎ ‎2‎ ‎0‎ C．‎ ‎1‎ ‎2‎ ‎0‎ D．‎ ‎8、（2010内蒙赤峰）已知反比例函数，当－4≤x≤－1时，y的最大值是___________.‎ ‎9、（2010陕西西安）已知都在反比例函数的图象上。若，则的值为 。‎ ‎10、（2010广西南宁）如图所示，点、、在轴上，且,分别过点、、作轴的平行线，与分比例函数的图像分别 交于点、、，分别过点、、作轴的平行线，分别与 轴交于点、、，连接、、,那么图中阴影部分的面积之和为 ． ‎ y x C B A D O ‎11、如图所示，在直角坐标系中，点是反比例函数的图象上一点，轴的正半轴于点，是的中点；一次函数的图象经过、两点，并将轴于点若 ‎（1）求反比例函数和一次函数的解析式；‎ ‎（2）观察图象，请指出在轴的右侧，当时，的取值范围．‎ ‎12、（2010广东湛江）病人按规定的剂量服用某种药物，测得服药后2小时，每毫升血液中的含量达到归大值为4毫克。已知服药后，2小时前每毫升血液中的含量y（毫克）与时间x（小时）成正比例；2小时后y与x成反比例（如图所示）。根据以上信息解答下列问题：‎ ‎(1).求当时，y与x的函数关系式；‎ ‎(2).求当时，y与x的函数关系式；‎ ‎(3).若每毫升血液中的含量不低于2毫克时治疗有效，则服药一次，治疗疾病的有效时间是多长？‎ ‎13、(2010江苏苏州) 如图，四边形OABC是面积为4的正方形，函数(x＞0)的图象经过点B．‎ ‎ (1)求k的值；‎ ‎ (2)将正方形OABC分别沿直线AB、BC翻折，得到正方形MABC′、MA′BC．设线段MC′、NA′分别与函数(x＞0)的图象交于点E、F，求线段EF所在直线的解析式．‎ 分式难题、易错题 ‎1. 从质量为m kg的一捆钢筋中截取一段长为5米的钢筋，称出这段钢筋的质量为n kg，则这捆钢筋的总长度为＿＿＿＿＿＿米 ‎2. 若值为整数，则x的整数值有＿＿＿个，分别是＿＿＿＿＿＿‎ ‎3. 下列各式中，与分式的值相等的是 （ ）‎ ‎ ‎ ‎4. 若把分式中的x，y的值都扩大2倍，则原分式的值 （ ）‎ A.不变 B.扩大2倍 C.扩大4倍 D.扩大8倍 ‎5. 已知 ，求的值 ‎6. 若m等于它的倒数，则分式的值为 （ ）‎ A.-2 B.4 C.-2或4 D.‎ ‎7. 化简： ‎ ‎8. 若x=2005 ， y=2006 ，则=＿＿＿＿＿‎ ‎9. 已知：x= ，y= ，则=＿＿＿＿＿‎ ‎10. 已知，，，则a、b、c的大小关系是＿＿＿＿＿‎ ‎11. 已知 ， ，求的值 ‎12. 关于x的方程的解为负数，则a的取值范围是＿＿＿＿＿‎ ‎13 .如果分式方程无解，那么m的值为＿＿＿＿＿‎ ‎14. 某地要筑一水坝，需要在规定日期内完成，如果由甲队去做，恰好如期完成；如果由乙队去做，则需超过规定日期三天。现由甲、乙两队合作2天后，余下的工程由乙队独做，恰好在规定日期完成，求规定的日期x （有两种不同的方法做）‎ ‎15. 若分式的值为0，则x的值为＿＿＿＿＿‎ ‎16. 若，则＿＿＿＿＿‎ ‎17. 已知实数x满足，则代数式的值为＿＿＿＿＿‎ ‎18. 计算：‎ ‎19. 甲乙两位采购员同去一家饲料公司购买两次饲料，第一次饲料的价格为a元/千克，第二次饲料的价格为b元/千克，且a≠b。两位采购员的购货方式不同，其中甲每次购买1000千克的饲料，而乙每次用800元钱购买饲料.‎ ‎ （1）甲、乙所购买的饲料的平均单价分别是多少？‎ ‎ （2）谁的购货方式更合算？请说明理由.‎