中考圆专题讲练5圆与相似一——求线段的长 4页

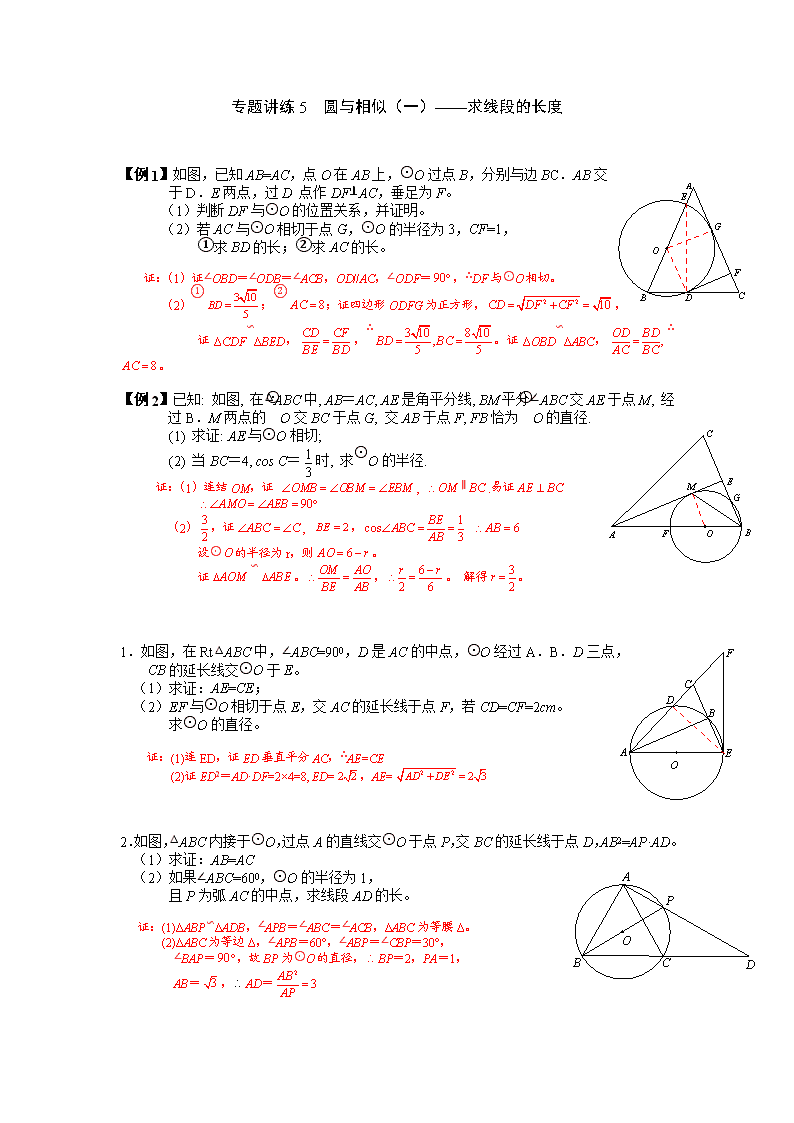
专题讲练5 圆与相似（一）——求线段的长度 ‎【例1】如图，已知AB=AC，点O在AB上，⊙O过点B，分别与边BC．AB交 于D．E两点，过D 点作DF⊥AC，垂足为F。‎ ‎（1）判断DF与⊙O的位置关系，并证明。‎ ‎（2）若AC与⊙O相切于点G，⊙O的半径为3，CF=1，‎ ‎①求BD的长；②求AC的长。‎ ‎ ‎ 证：（1）证∠OBD＝∠ODB＝∠ACB，OD//AC，∠ODF＝，∴DF与⊙O相切。‎ ‎（2）①；②；证四边形ODFG为正方形，，‎ 证ΔCDF∽ΔBED，，∴。证ΔOBD∽ΔABC，∴。‎ ‎【例2】已知: 如图, 在△ABC中, AB＝AC, AE是角平分线, BM平分∠ABC交AE于点M, 经过B．M两点的⊙O交BC于点G, 交AB于点F, FB恰为⊙O的直径.‎ ‎ (1) 求证: AE与⊙O相切;‎ ‎ (2) 当BC＝4, cos C＝时, 求⊙O的半径.‎ 证：（1）连结OM，证 , ∥.易证 ‎（2），证, ， ‎ 设⊙的半径为r，则。‎ 证∽。，。 解得。‎ ‎1．如图，在Rt△ABC中，∠ABC=900，D是AC的中点，⊙O经过A．B．D三点，‎ CB的延长线交⊙O于E。‎ ‎（1）求证：AE=CE；‎ ‎（2）EF与⊙O相切于点E，交AC的延长线于点F，若CD=CF=2cm。‎ 求⊙O的直径。‎ 证：(1)连ED，证ED垂直平分AC，∴AE=CE ‎(2)证ED2＝AD·DF=2×4=8, ED=，AE=‎ ‎2．如图，△ABC内接于⊙O，过点A的直线交⊙O于点P，交BC的延长线于点D，AB2=AP·AD。‎ ‎（1）求证：AB=AC ‎（2）如果∠ABC=600，⊙O的半径为1，‎ 且P为弧AC的中点，求线段AD的长。‎ ‎ ‎ 证：(1)ΔABP∽ΔADB，∠APB＝∠ABC＝∠ACB，ΔABC为等腰Δ。‎ ‎(2)ΔABC为等边Δ，∠APB＝60°，∠ABP＝∠CBP＝30°，‎ ‎∠BAP＝，故BP为⊙O的直径，BP＝2，PA＝1，‎ AB＝，AD＝‎ ‎3．如图，直线MN交⊙O于A．B两点，AC是直径。AD平分∠CAM，交⊙O于D，过D作DE⊥MN于E点。‎ ‎（1）求证：DE是⊙O的切线 ‎（2）若DE=6cm，AE=3cm，求⊙O的半径。‎ ‎ ‎ 证：（1）连OD．DC，证∠DAE＝∠OAD＝∠ODA，OD//AE；‎ ‎（2）；易求，证ΔADE∽ΔACD，‎ ‎，∴AC＝15，‎ K ‎4．如图，已知⊙O的直径AB=4。过B点作⊙O的切线MN，D．C是⊙O上的两点，连接AD．BD．CD和BC。‎ ‎（1）求证：∠CBN=∠CDB；‎ ‎（2）若DC是∠ADB的平分线，且∠DAB=150，求DC的长。‎ ‎ ‎ ‎ 证：（1）连AC，∠CDB＝∠CAB，∠CAB+∠CBA＝，∠CBN+∠CBA＝，‎ ‎　∴‎ ‎（2）作CK⊥AD于K，证＝∠CAB＝∠CBA，∠CAD＝，，‎ ‎，证CK＝DK，,∴‎ ‎5．如图，AB为⊙O的直径，PQ与⊙O相切于点T，过A点作AC⊥PQ于C点，交⊙O于D点。‎ ‎（1）求证：AT平分∠BAC ‎（2）若AD=2，TC=，求⊙O的半径。‎ 证：（1）连OT，OT//AC，∠OAT＝∠OTA＝∠TAC ‎（2）连BD，BD//TC，OT⊥BD，BD＝2CT＝，‎ AB＝，R＝2‎ ‎6．如图，AB．BC．CD分别与⊙O相切于E、F、G三点，且AB∥CD，连接OB．OC，‎ 延长CO交⊙O于点M，过点M作MN∥OB交CD于N点。‎ ‎（1）求证：MN是⊙O的切线。‎ ‎（2）当OB=6cm，OC=8cm时，求⊙O的半径及MN的长。‎ ‎ ‎ ‎ 证：（1）证∠ABC+∠BCD＝，∠ABO＝∠CBO，∠BCO＝∠DCO ‎∠CBO+∠BCO＝＝∠BOM＝∠CMN ‎（2）连OF，，‎ 证ΔCOB∽ΔCMN，‎ 即 ‎7．如图，已知⊙O是△ABC的外接圆，AB是⊙O的直径，D是AB延长线上的一点，AE⊥CD交DC的延长线于E，CF⊥AB于点F，且CE=CF。‎ ‎（1）求证：DE是⊙O的切线。‎ ‎（2）若AB=6，BD=3，求AE和BC的长。‎ ‎ 证：（1）连OC，‎ ‎∴∥，∴‎ ‎（2），，‎ 证ΔAEC∽ΔACB，,∴‎ ‎ ‎ ‎8．如图，AB．AC分别是⊙O的直径和弦，点D为劣弧AC上一点，DE⊥AB于点H，‎ 交⊙O于点E，交AC于点F。点P为ED延长线上一点，连PC。‎ ‎（1）若PC与⊙O相切，判断△PCF的形状，并证明。‎ ‎（2）若D为弧AC的中点，且，DH=8，求⊙O的半径。‎ 证：（1）连OC，∠OCA＝∠OAC，∠OCA+∠PCF＝，∠PFC+∠OAC＝，‎ ‎∠PCF＝∠PFC，‎ ‎（2）设，则，证，则，‎ ‎9．如图，AB为⊙O的直径，点D为⊙O上一点，CD=BD。过D点作DE⊥AC，垂足为E点，延长DE交 BA的延长线于 P点。‎ ‎（1）求证：DE为⊙O的切线。‎ ‎（2）若AB=6，AD=，求PE的长。‎ ‎ 证：（1） 证，∠ODE＝∠DEC＝‎ ‎（2）证ΔAED∽ΔADB，，‎ ΔPEA∽ΔPDO，‎ ‎10．如图，已知⊙O的半径为‎6cm，射线PM经过点O，OP=‎10cm，射线PN与⊙O相切于点Q，A．B两点同时从点P出发，点A以‎5cm/s的速度沿射线PM方向运动，点B以‎4cm/s的速度沿射线PN方向运动，设运动时间为ts。‎ ‎（1）求PQ的长。‎ ‎（2）当t为何值时，直线AB与⊙O相切？‎ ‎ 证：（1）PQ＝‎‎8cm ‎（2）或，分两种情况：‎ ‎①直线AB与⊙O第一次相切时，设切点为F，则PA＝5t,PB＝4t，‎ ‎，又∠P公共，‎ ‎∴ΔPAB∽ΔPOQ，，易证四边形OFBQ为正方形，QB＝8－4t＝OQ＝6，‎ ‎②直线AB与⊙O第二次相切时，同理可得，QB＝4t-8=OQ=6，‎ ‎11．如图在Rt△ABC中，BC=9，CA=12，∠ABC的平分线BD交AC于点D，过D点作DE⊥DB交AB于点E。‎ ‎（1）设⊙O是△BDE的外接圆，求证：AC是⊙O的切线。‎ ‎（2）设⊙O交BC于点F，连结EF，求的值。‎ ‎ 证： (1)证∠DBC=∠DBO=∠ODB,OD//BC, ∴∠ODA＝∠C＝90°。‎ ‎(2)9；证∠EFB＝90°＝∠C，EF//AC，ΔBEF∽ΔBAC，‎ 易求AB=15，设EF＝4x，BF＝3x,则EB＝5x，OD＝‎ 证ΔOAD∽ΔBAC，，∴，EF＝4x＝9‎ ‎12．如图，BC为⊙O的直径，点F在⊙O上，∠FCA=∠FOC，CD=AD，AB交⊙O点E.‎ ‎（1）求证：CA为⊙O的切线；‎ ‎（2）若EF=1.5，CF=2，BE=4，求⊙O的半径.‎ 证：(1) 略 (2) 连CE, ∵△BCF∽△BCD, ‎ ‎∴①证，△BEF∽△BAD, ∴②‎ 又AD=CD, 由①、②可得, ∴BC=, ∴R=.‎