中考数学专题复习几何证明压轴题含答案解析 6页

几何证明压轴题（中考）‎ ‎1、如图，在梯形ABCD中，AB∥CD，∠BCD=90°,且AB=1，BC=2，tan∠ADC=2.‎ (1) 求证：DC=BC;‎ (2) E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论；‎ (3) 在（2）的条件下，当BE：CE=1：2，∠BEC=135°时，求sin∠BFE的值. ‎ ‎[解析] （1）过A作DC的垂线AM交DC于M,‎ 则AM=BC=2.‎ 又tan∠ADC=2,所以.即DC=BC.‎ ‎(2)等腰三角形.‎ 证明：因为.‎ 所以，△DEC≌△BFC 所以，.‎ 所以，‎ 即△ECF是等腰直角三角形.‎ ‎（3）设,则，所以.‎ 因为，又，所以.‎ 所以 所以.‎ ‎2、已知：如图，在□ABCD 中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．‎ ‎（1）求证：△ADE≌△CBF；‎ ‎（2）若四边形 BEDF是菱形，则四边形AGBD是什么特殊四边形？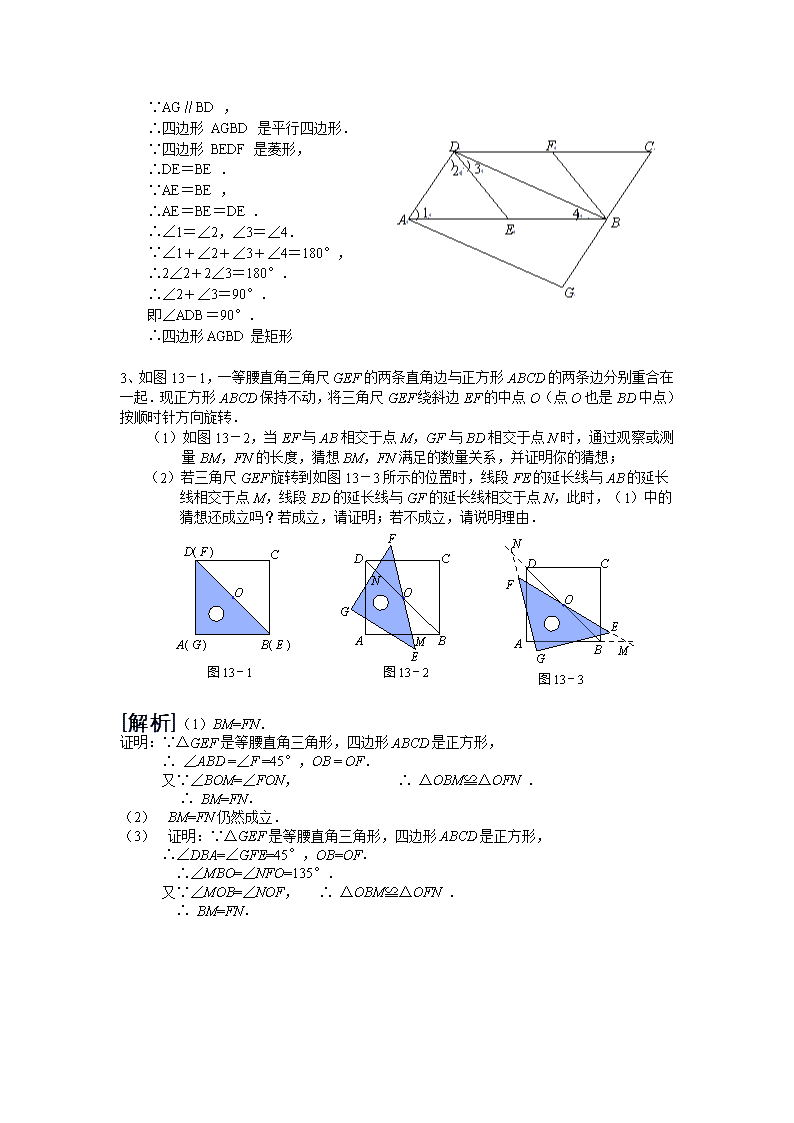并证明你的结论．‎ ‎[解析] （1）∵四边形ABCD是平行四边形，‎ ‎∴∠1＝∠C，AD＝CB，AB＝CD ． ‎ ‎∵点E 、F分别是AB、CD的中点，‎ ‎∴AE＝AB ，CF＝CD ．‎ ‎∴AE＝CF ‎∴△ADE≌△CBF ． ‎ ‎（2）当四边形BEDF是菱形时，‎ 四边形 AGBD是矩形．‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC ．‎ ‎∵AG∥BD ，‎ ‎∴四边形 AGBD 是平行四边形． ‎ ‎∵四边形 BEDF 是菱形，‎ ‎∴DE＝BE ．‎ ‎∵AE＝BE ，‎ ‎∴AE＝BE＝DE ．‎ ‎∴∠1＝∠2，∠3＝∠4．‎ ‎∵∠1＋∠2＋∠3＋∠4＝180°，‎ ‎∴2∠2＋2∠3＝180°．‎ ‎∴∠2＋∠3＝90°．‎ 即∠ADB＝90°． ‎ ‎∴四边形AGBD是矩形 ‎3、如图13－1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．‎ ‎（1）如图13－2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；‎ 图13－1‎ A( G )‎ B( E )‎ C O D( F )‎ 图13－2‎ E A B D G F O M N C ‎（2）若三角尺GEF旋转到如图13－3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．‎ 图13－3‎ A B D G E F O M N C ‎[解析]（1）BM=FN． ‎ 证明：∵△GEF是等腰直角三角形，四边形ABCD是正方形，‎ ‎∴ ∠ABD =∠F =45°，OB = OF．‎ 又∵∠BOM=∠FON， ∴ △OBM≌△OFN ．‎ ‎∴ BM=FN． ‎ （1） BM=FN仍然成立． ‎ （2） 证明：∵△GEF是等腰直角三角形，四边形ABCD是正方形，‎ ‎∴∠DBA=∠GFE=45°，OB=OF．‎ ‎∴∠MBO=∠NFO=135°．‎ 又∵∠MOB=∠NOF， ∴ △OBM≌△OFN ．‎ ‎∴ BM=FN． ‎ ‎4、如图，已知⊙O的直径AB垂直于弦CD于E，连结AD、BD、OC、OD，且OD＝5。‎ ‎ （1）若，求CD的长；‎ ‎ （2）若 ∠ADO：∠EDO＝4：1，求扇形OAC（阴影部分）的面积（结果保留）。‎ ‎[解析] （1）因为AB是⊙O的直径，OD＝5‎ ‎ 所以∠ADB＝90°，AB＝10 ‎ ‎ 在Rt△ABD中，‎ ‎ 又，所以，所以 ‎ ‎ ‎ 因为∠ADB＝90°，AB⊥CD ‎ 所以 ‎ 所以 ‎ 所以 ‎ 所以 ‎ ‎ （2）因为AB是⊙O的直径，AB⊥CD ‎ 所以 ‎ 所以∠BAD＝∠CDB，∠AOC＝∠AOD ‎ 因为AO＝DO，所以∠BAD＝∠ADO ‎ 所以∠CDB＝∠ADO ‎ 设∠ADO＝4x，则∠CDB＝4x ‎ 由∠ADO：∠EDO＝4：1，则∠EDO＝x ‎ 因为∠ADO＋∠EDO＋∠EDB＝90°‎ ‎ 所以 ‎ 所以x＝10°‎ ‎ 所以∠AOD＝180°－（∠OAD＋∠ADO）＝100°‎ ‎ 所以∠AOC＝∠AOD＝100°‎ ‎ ‎ ‎5、如图，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G. ‎（1）求证：点F是BD中点；‎ ‎（2）求证：CG是⊙O的切线；‎ ‎（3）若FB=FE=2，求⊙O的半径．‎ ‎[解析] (1)证明：∵CH⊥AB，DB⊥AB，∴△AEH∽AFB，△ACE∽△ADF ‎∴，∵HE＝EC，∴BF＝FD ‎ ‎(2)方法一：连接CB、OC，‎ ‎∵AB是直径，∴∠ACB＝90°∵F是BD中点，‎ ‎∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO ‎∴∠OCF=90°,∴CG是⊙O的切线---------6′‎ 方法二：可证明△OCF≌△OBF(参照方法一标准得分)‎ ‎ (3)解：由FC=FB=FE得：∠FCE=∠FEC ‎ 可证得：FA＝FG，且AB＝BG 由切割线定理得：（2＋FG）2＝BG×AG=2BG2 在Rt△BGF中，由勾股定理得：BG2＝FG2－BF2　 由、得：FG2-4FG-12=0‎ 解之得：FG1＝6，FG2＝－2（舍去）‎ ‎∴AB＝BG＝‎ ‎∴⊙O半径为2‎ ‎6、如图，已知O为原点，点A的坐标为（4，3），‎ ‎⊙A的半径为2．过A作直线平行于轴，点P在直线上运动．‎ ‎（１）当点P在⊙O上时，请你直接写出它的坐标；‎ ‎（２）设点P的横坐标为12，试判断直线OP与⊙A的位置关系，并说明理由.‎ ‎[解析]‎ 解: ⑴点P的坐标是（2,3）或（6,3）‎ ⑵作AC⊥OP,C为垂足.‎ ‎∵∠ACP=∠OBP=,∠1=∠1‎ ‎∴△ACP∽△OBP ‎ ‎∴ ‎ ‎ 在中,,又AP=12-4=8, ∴‎ ‎∴AC=≈1.94 ‎ ‎∵1.94<2‎ ‎∴OP与⊙A相交. ‎ ‎7、如图，延长⊙O的半径OA到B，使OA=AB，‎ DE是圆的一条切线，E是切点，过点B作DE的垂线，‎ C A B D O E 垂足为点C.‎ 求证：∠ACB=∠OAC.‎ ‎[解析]‎ 证明：连结OE、AE，并过点A作AF⊥DE于点F， （3分）‎ ‎∵DE是圆的一条切线，E是切点，‎ ‎∴OE⊥DC，‎ 又∵BC⊥DE,‎ ‎∴OE∥AF∥BC. ‎ ‎ ∴∠1=∠ACB，∠2=∠3.‎ ‎∵OA=OE，‎ ‎∴∠4=∠3. ‎ ‎∴∠4=∠2. ‎ 又∵点A是OB的中点，‎ ‎∴点F是EC的中点. ‎ ‎∴AE=AC. ‎ ‎∴∠1=∠2. ‎ ‎∴∠4=∠2=∠1. ‎ ‎ 即∠ACB=∠OAC.‎ ‎8、如图１，一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上，梯子与地面的倾斜角α为．‎ ⑴求AO与BO的长；‎ ⑵若梯子顶端A沿NO下滑，同时底端B沿OM向右滑行.‎ ‎①如图2，设A点下滑到C点，B点向右滑行到D点，并且AC:BD=2:3，试计算梯子顶端A沿NO下滑多少米；‎ ‎②如图３，当A点下滑到A’点，B点向右滑行到B’点时，梯子AB的中点P也随之运动到P’点．若∠POP’＝ ，试求AA’的长．‎ ‎[解析]‎ ⑴中,∠O=,∠α=‎ ‎∴,∠OAB=，又ＡＢ＝4米，‎ ‎ ∴米.‎ 米. -------------- (3分)‎ ⑵设在中,‎ ‎ ‎ ‎ 根据勾股定理:‎ ‎∴ ------------- (5分) ‎ ‎∴‎ ‎∵　　∴‎ ‎ ∴ ------------- (7分)‎ AC=2x=‎ 即梯子顶端A沿NO下滑了米. ---- (8分)‎ ⑶∵点P和点分别是的斜边AB与的斜边的中点 ‎∴， ------------- (9分)‎ ‎∴------- (10分)‎ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴ ----------------------- (11分)‎ ‎∴----- (12分)‎ ‎∴米. -------- (13分)‎