南京市中考模拟数学测试卷玄武一模及答案 12页

‎2016年南京市中考模拟数学测试卷（玄武一模）‎ 全卷满分120分．考试时间为120分钟．‎ 一、选择题（本大题共6小题，每小题2分，共12分．）‎ ‎1．下列运算正确的是 A．a3＋a3＝a6‎ B．2(a＋1)＝2a＋1‎ C．(ab)2＝a2b2‎ D．a6÷a3＝a2‎ ‎2．下列各数中，是无理数的是 A．cos30°‎ B．(－π)0‎ C．－ D． ‎3．计算2－1×8－的结果是 A．－21‎ B．－1‎ C．9‎ D．11‎ ‎4．体积为80的正方体的棱长在 A．3到4之间 B．4到5之间 C．5到6之间 D．6到7之间 ‎5．如图，将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的，长度不变，AB、BC的长度也不变，则∠ABC的度数大小由60°变为 A．°‎ B．°‎ C．°‎ D．°‎ A B A B C C ‎（第5题）‎ ‎ ‎y x O A B C P Q ‎（第6题）‎ ‎6．如图，正方形OABC的边长为6，A，C分别位于x轴、y轴上，点P在AB上，CP交OB于点Q，函数y＝的图象经过点Q，若S△BPQ＝S△OQC，则k的值为 A．－12‎ B．12‎ C．16‎ D．18‎ 二、填空题（本大题共10小题，每小题2分，共20分．）‎ O A B ‎（第12题）‎ ‎7．使式子1＋有意义的x的取值范围是 ▲ ．‎ ‎8．计算：－＝ ▲ ．‎ ‎9．有一组数据：1，3，3，4，4，这组数据的方差为 ▲ ．‎ ‎10．设x1，x2是方程x2＋4x＋3＝0的两根，则x1＋x2＝ ▲ ．‎ ‎11．今年清明假期全国铁路发送旅客约41 000 000人次，将41 000 000用科学记数法表示为 ▲ ．‎ ‎12．如图，已知⊙O的半径为13，弦AB长为24，则点O到AB的距离是 ▲ ．‎ ‎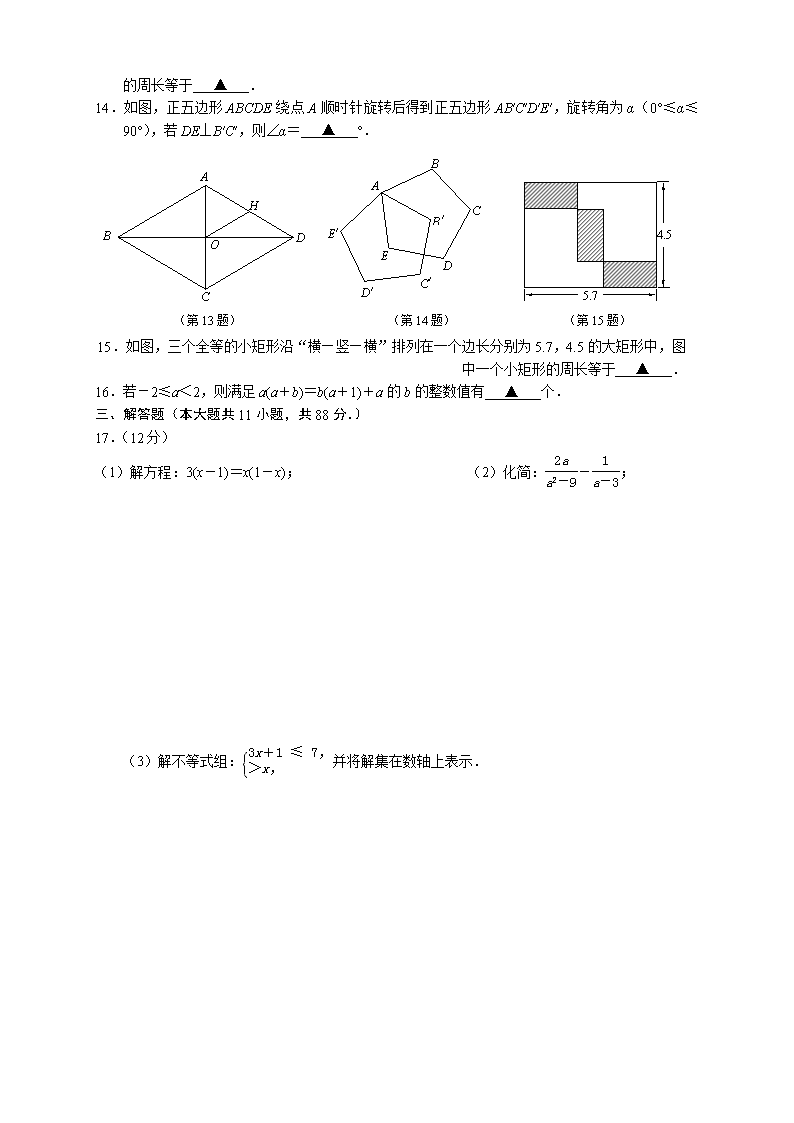13．如图，菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，OH＝8，则菱形ABCD的周长等于 ▲ ．‎ ‎14．如图，正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′，旋转角为α（0°≤α≤90°），若DE⊥B′C′，则∠α＝ ▲ °．‎ A B C D O H ‎（第13题）‎ ‎ A B C D E B′‎ C′‎ D′‎ E′‎ ‎（第14题）‎ ‎‎4.5‎ ‎5.7‎ ‎（第15题）‎ ‎15．如图，三个全等的小矩形沿“横—竖—横”排列在一个边长分别为5.7，4.5的大矩形中，图中一个小矩形的周长等于　 ▲ 　．‎ ‎16．若－2≤a＜2，则满足a(a＋b)＝b(a＋1)＋a的b的整数值有 ▲ 个．‎ 三、解答题（本大题共11小题，共88分．）‎ ‎17．（12分）‎ ‎（1）解方程：3(x－1)＝x(1－x)； （2）化简：－；‎ ‎（3）解不等式组：并将解集在数轴上表示．‎ ‎18．（7分）如图，□ABCD的对角线AC、BD相交于点O，AE＝CF．‎ ‎（1）求证：△BOE≌△DOF；‎ ‎（2）若BD＝EF，连接DE、BF，判断四边形EBFD的形状，并说明理由.‎ O C B A D F E ‎（第18题）‎ ‎19．（7分）从甲、乙、丙3名同学中随机抽取一名同学参与问卷调查，求下列事件的概率：‎ ‎（1）抽取1名，恰好是甲；‎ ‎（2）抽取2名，甲在其中．‎ ‎20．（7分）元宵节那天，李老师给他的微信好友群发了一个小调查：“‎ 元宵节，你选择吃大汤圆，还是小元宵呢？”12小时内好友回复的相关数据如下图：‎ ‎200‎ 人数 回复 的人 大汤圆 小元宵 项目 ‎80‎ ‎150‎ 不超过 ‎0.5小时 ‎0.5小时 ‎~1小时 ‎1小时 ‎~5小时 ‎5小时 ‎~12小时 ‎50%‎ ‎30%‎ ‎15%‎ 回复人数及选择情况条形统计图 好友回复时间扇形统计图 ‎（第20题）‎ ‎0‎ ‎（1）回复时间为5小时~12小时的人数为 ▲ ；‎ ‎（2）既选择大汤圆，又选择小元宵的人数为 ▲ ；‎ ‎（3）12小时后，又有40个好友回复了，如果重新制作“好友回复时间扇形统计图”，加入“12小时后”这一项，求该项所在扇形的圆心角度数．‎ ‎21．（7分）如图，点P、M、Q在半径为1的⊙O上，根据已学知识和图中数据（0.97、0.26为近似数），解答下列问题：‎ ‎（1）sin60°＝ ▲ ；cos75°＝ ▲ ；‎ ‎（2）若MH⊥x轴，垂足为H，MH交OP于点N，求MN的长．（结果精确到0.01，参考数据：≈1.414，≈1.732）‎ ‎75°‎ ‎60°‎ ‎15°‎ x O P Q M N H ‎0.97‎ ‎1‎ ‎0.26‎ ‎0.97‎ ‎0.26‎ ‎1‎ y ‎（第21题）‎ ‎22．（8分）二次函数y＝ax2＋bx＋c的图象经过点（0，3），（3，6），（－2，11）．‎ ‎（1）求该二次函数的关系式；‎ ‎（2）证明：无论x取何值，函数值y总不等于1；‎ ‎（3）如何平移该函数图象使得函数值y能等于1？‎ ‎23．（7分）如图，已知△ABC，△DCE是两个全等的等腰三角形，底边BC、CE在同一直线上，且AB＝，BC＝1．BD与AC交于点P．‎ ‎（1）求证：△BDE∽△DEC；‎ ‎（2）求△DPC的周长．‎ A B C D E P ‎（第23题）‎ ‎24．（8分）如图，AB是⊙O的直径，点D、E在⊙O上，连接AE、ED、DA，连接BD并延长至点C，使得∠DAC＝∠AED．‎ A B C D E F O ‎（第24题）‎ ‎（1）求证：AC是⊙O的切线；‎ ‎（2）若点E是的中点，AE与BC交于点F，‎ ‎①求证：CA＝CF；‎ ‎②当BD＝5，CD＝4时，DF＝ ▲ ．‎ ‎25．（7分）随着“互联网＋”时代的到来，一种新型打车方式受到大众欢迎．该打车方式的计价规则如图①所示，若车辆以平均速度v km/h行驶了s km，则打车费用为（ps＋60q·）元（不足9元按9元计价）．小明某天用该打车方式出行，按上述计价规则，其打车费用y（元）与行驶里程x（km）的函数关系也可由如图②表示．‎ x(km)‎ O ‎6‎ ‎9‎ ‎12‎ ‎8‎ y(元)‎ ‎（第25题）‎ ‎0元起步费 p元 / 公里 q元 / 1分钟 ‎9元最低消费 ‎＋‎ ‎＋‎ 计价规则 ‎①‎ ‎②‎ ‎（1）当x≥6时，求y与x的函数关系式；‎ ‎（2）若p＝1，q＝0.5，求该车行驶的平均速度．‎ ‎26．（8分）某日王老师佩戴运动手环进行快走锻炼，两次锻炼后数据如下表．与第一次锻炼相比，王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．设王老师第二次锻炼时平均步长减少的百分率为x（0＜x＜0.5）．‎ 项目 第一次锻炼 第二次锻炼 步数（步）‎ ‎10000‎ ‎① ▲ ‎ 平均步长（米/步）‎ ‎0.6‎ ‎② ▲ ‎ 距离（米）‎ ‎6000‎ ‎7020‎ 注：步数×平均步长＝距离．‎ ‎（1）根据题意完成表格填空；‎ ‎（2）求x；‎ ‎（3）王老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求王老师这500米的平均步长．‎ ‎27．（10分）如图①，现有长度分别为a、b、1的三条线段．‎ a b ‎1‎ ‎①‎ ‎ ‎a b a＋b ‎②‎ ‎【加、减】图②所示为长为a＋b的线段，请用尺规作出长为a－b的线段．‎ ‎【乘】在图③中，OA＝a，OC＝b，点B在OA上，OB＝1，AD∥BC，交射线OC于点D．‎ 求证：线段OD的长为ab．‎ O A C B D ‎③‎ ‎【除】请用尺规作出长度为的线段．‎ ‎【开方】任意两个有理数的和、差、积、商（除数不为0）仍然是有理数，而开方运算则打开了通向无理数的一扇门．请用两种不同的方法，画出长度为 的线段．‎ 注：本题作（画）图不写作（画）法，需标明相应线段长度．‎ 数学试题参考答案及评分标准 说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．‎ 一、选择题（本大题共6小题，每小题2分，共12分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 答案 C A B B D C 二、填空题（本大题共10小题，每小题2分，共20分）‎ ‎7． x≠1 8． 9． 1.2 10．－4 11．4.1×107 ‎ ‎12．5 13．64 14． 54° 15． 6.8 16．7‎ 三、解答题（本大题共11小题，共88分）‎ ‎17．（本题12分）‎ ‎（1）（本题4分）‎ 解：3(x－1) ＝－x(x－1)‎ ‎3(x－1)＋x(x－1)＝0‎ ‎(x－1) (x＋3)＝0‎ x1＝1，x2＝－3． 4分 ‎（2）（本题4分）‎ 解：－＝－＝＝＝．‎ ‎8分 ‎（3）（本题4分） 解：解不等式①，得x≤2，‎ 解不等式②，得x＜－1，‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎－1‎ ‎－2‎ ‎－3‎ 不等式组的解集为x＜－1． 12分 ‎18．（本题7分）‎ ‎（1）证明：∵四边形ABCD为平行四边形 ‎ ∴BO＝DO，AO＝CO．‎ ‎ ∵AE＝CF，‎ ‎ ∴AO－AE＝CO－CF，即EO＝FO．‎ ‎ 在△BOE与△DOF中 ‎∴△BOE≌△DOF． 4分 ‎（2）四边形EBFD为矩形．‎ ‎ ∵EO＝FO，BO＝DO，‎ ‎ ∴四边形EBFD为平行四边形．‎ ‎ ∵BD＝EF，‎ ‎ ∴四边形EBFD为矩形． 7分 ‎19．（本题7分）‎ 解：（1）从甲、乙、丙3名同学中随机抽取1名同学参与问卷调查，恰好是甲的概率是．‎ ‎ 3分 ‎（2）从甲、乙、丙3名同学中随机抽取2名同学参与问卷调查，所有可能出现的结果有：（甲，乙）、（甲，丙）、（乙，丙），共有3种，它们出现的可能性相同．所有的结果中，满足“甲在其中”（记为事件A）的结果只有2种，所以P(A)＝． 7分 ‎20．（本题7分）‎ ‎（1）10； 2分 ‎（2）30； 4分 ‎（3）解：×360°＝60°．答：“12小时后”这一项所在扇形的圆心角度数为60°．‎ ‎ 7分 ‎21．（本题7分）‎ ‎75°‎ ‎60°‎ ‎15°‎ x O P Q M N H ‎0.97‎ ‎1‎ ‎0.26‎ ‎0.97‎ ‎0.26‎ ‎1‎ y A 解：（1）；0.26； ‎ ‎（2）在Rt△MHO中，sin∠MOH＝，‎ 即MH＝MO·sin∠MOH＝1×＝．‎ ‎∴OH＝＝．‎ 设PA⊥x轴，垂足为A，‎ ‎∵∠NHO＝∠PAO＝90°，‎ ‎∴NH∥PA，‎ ‎∴＝，即＝，‎ ‎∴NH≈0.134．‎ ‎∴MN＝MH－MN≈0.73． 7分 ‎22．（本题8分）‎ ‎（1）解：由题意得：，解得： ‎∴该函数的函数关系式为：y＝x2－2x＋3． 3分 ‎（2）证明：∵y＝x2－2x＋3＝(x－1)2＋2，‎ ‎∴当x＝1时，y取最小值2，‎ ‎∴无论x取何值，函数值y总不等于1． 6分 ‎（3）将该函数图象向下平移的距离大于等于1个单位长度． 8分 ‎23．（本题7分）‎ ‎（1）证明：∵△ABC，△DCE是两个全等的等腰三角形，且底边BC、CE在同一直线上，‎ ‎∴AB＝AC＝DC＝DE＝，BC＝CE＝1，‎ ‎∴BE＝2BC＝2．‎ ‎∵＝，＝，‎ ‎∴＝．‎ 又∵∠BED＝∠DEC，‎ ‎∴△BED∽△DEC． 4分 ‎（2）解： ∵△ABC，△DCE是两个全等的等腰三角形，且底边BC、CE在同一直线上，‎ ‎∴∠ACB＝∠DEC，‎ ‎∴AC∥DE．‎ ‎∴＝＝．‎ ‎∴PC＝，PD＝1，‎ ‎∴△DPC的周长＝PC＋PD＋DC＝＋1＋＝＋1． 7分 ‎24．（本题8分）‎ ‎（1）证明：∵AB是⊙O的直径，‎ ‎ ∴∠ADB＝90°．‎ ‎ ∴∠ABC＋∠DAB＝90°．‎ ‎ ∵∠DAC＝∠AED，∠AED＝∠ABC，‎ ‎ ∴∠DAC ＋∠DAB＝90°，‎ ‎ ∴ AC是⊙O的切线． 3分 ‎（2）①证明：∵点E是的中点，‎ ‎∴＝，‎ ‎∴∠BAE＝∠DAE．‎ ‎∵∠DAC ＋∠DAB＝90°，∠ABC＋∠DAB＝90°，‎ ‎∴∠DAC＝∠ABC．‎ ‎∵∠CFA＝∠ABC＋∠BAE，∠CAF＝∠DAC＋∠DAE，‎ ‎∴∠CFA＝∠CAF．‎ ‎∴ CA＝CF． 6分 ‎②DF＝2． 8分 ‎25．（本题7分）‎ 解：（1）当x≥6时，设y与x之间的函数关系式为y＝kx＋b．‎ 根据题意，当x＝6时，y＝9；当x＝8时，y＝12．‎ 所以解得 所以，y与x之间的函数关系式为y＝1.5x． 4分 ‎（2）根据图象可得，当x＝8时，y＝12，‎ 又因为p＝1，q＝0.5，‎ 可得12＝1·8＋60·0.5·，‎ 解得v＝60．经检验，v＝60是原方程的根．‎ 所以该车行驶的平均速度为60 km/h． 7分 ‎26．（本题8分）‎ ‎（1）① 10000(1＋3x)；② 0.6(1－x)． ‎ ‎（2）解： 由题意：10000(1＋3x)× 0.6(1－x)＝7020‎ ‎ 解得：x1＝＞0.5（舍去），x2＝0.1．‎ ‎∴ x＝0.1． 6分 ‎（3）解：10000＋10000(1＋0.1×3)＝23000，‎ ‎500÷（24000－23000）＝0.5．‎ 答：王老师这500米的平均步长为0.5米 8分 ‎27．（本题10分）‎ ‎【加、减】如图①，线段AB长为a－b． 2分 b a－b A B a ‎①‎ ‎②‎ O A C B D a b ‎1‎ ‎【乘】证明：∵AD∥BC，∴＝，即＝．∴OD＝ab． 5分 ‎【除】如图②，OA＝a，OC＝b，点B在OC上，OB＝1，BD∥AC，交OA于点D．‎ 则OD＝． 7分 ‎【开方】图③和图④中的MN均为．‎ a b ‎1‎ N ‎③‎ ‎④‎ M O a b ‎1‎ M N O ‎ 10分