中考数学总复习训练多边形与平面镶嵌含解析20170711352 19页

多边形与平面镶嵌 一、选择题 ‎1．一个多边形的内角和是900°，则这个多边形的边数是（　　）‎ A．6 B．‎7 ‎C．8 D．9‎ ‎2．若一个多边形的内角和为1080°，则这个多边形的边数为（　　）‎ A．6 B．‎7 ‎C．8 D．9‎ ‎3．正十边形的每个外角等于（　　）‎ A．18° B．36° C．45° D．60°‎ ‎4．正六边形的每个内角都是（　　）‎ A．60° B．80° C．100° D．120°‎ ‎5．一个多边形的内角和与外角和相等，则这个多边形是（　　）‎ A．四边形 B．五边形 C．六边形 D．八边形 ‎6．如果一个多边形的内角和是其外角和的一半，那么这个多边形是（　　）‎ A．六边形 B．五边形 C．四边形 D．三角形 ‎7．一个正多边形的每个外角都等于36°，那么它是（　　）‎ A．正六边形 B．正八边形 C．正十边形 D．正十二边形 ‎8．只用下列图形中的一种，能够进行平面镶嵌的是（　　）‎ A．正十边形 B．正八边形 C．正六边形 D．正五边形 ‎9．下列图形中，单独选用一种图形不能进行平面镶嵌的是（　　）‎ A．正三角形 B．正六边形 C．正方形 D．正五边形 ‎10．一个多边形截取一个角后，形成另一个多边形的内角和是1620°，则原来多边形的边数是（　　）‎ A．10 B．‎11 ‎C．12 D．以上都有可能 ‎11．如图，过正五边形ABCDE的顶点A作直线l∥BE，则∠1的度数为（　　）‎ A．30° B．36° C．38° D．45°‎ ‎12．如图，甲、乙两人想在正五边形ABCDE内部找一点P，使得四边形ABPE为平行四边形，其作法如下：‎ ‎（甲） 连接BD、CE，两线段相交于P点，则P即为所求 ‎（乙） 先取CD的中点M，再以A为圆心，AB长为半径画弧，交AM于P点，则P即为所求．‎ 对于甲、乙两人的作法，下列判断何者正确？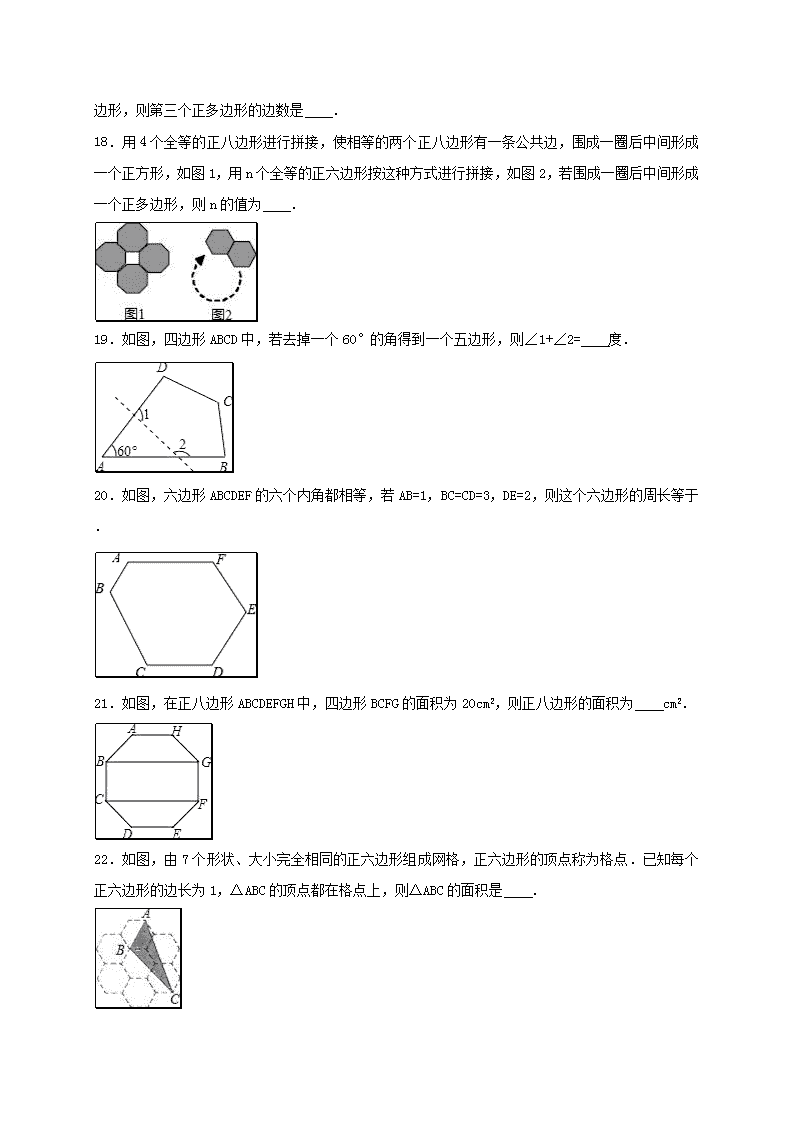（　　）‎ A．两人皆正确 B．两人皆错误 C．甲正确，乙错误 D．甲错误，乙正确 ‎13．如图，小红做了一个实验，将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，所转过的度数是（　　）‎ A．60° B．72° C．108° D．120°‎ ‎　‎ 二、填空题 ‎14．正n边形的一个外角的度数为60°，则n的值为　　．‎ ‎15．如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角．若∠A=120°，则∠1+∠2+∠3+∠4=　　．‎ ‎16．△OAB是以正多边形相邻的两个顶点A，B与它的中心O为顶点的三角形，若△OAB的一个内角为70°，则该正多边形的边数为　　．‎ ‎17．一幅图案在某个顶点处由三个边长相等的正多边形镶嵌而成．其中的两个分别是正方形和正六边形，则第三个正多边形的边数是　　．‎ ‎18．用4个全等的正八边形进行拼接，使相等的两个正八边形有一条公共边，围成一圈后中间形成一个正方形，如图1，用n个全等的正六边形按这种方式进行拼接，如图2，若围成一圈后中间形成一个正多边形，则n的值为　　．‎ ‎19．如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=　　度．‎ ‎20．如图，六边形ABCDEF的六个内角都相等，若AB=1，BC=CD=3，DE=2，则这个六边形的周长等于　　．‎ ‎21．如图，在正八边形ABCDEFGH中，四边形BCFG的面积为‎20cm2，则正八边形的面积为　　cm2．‎ ‎22．如图，由7个形状、大小完全相同的正六边形组成网格，正六边形的顶点称为格点．已知每个正六边形的边长为1，△ABC的顶点都在格点上，则△ABC的面积是　　．‎ ‎23．如图，正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置．若正六边形的边长为‎2cm，则正六边形的中心O运动的路程为　　cm．‎ ‎24．如图，将正六边形绕其对称中心O旋转后，恰好能与原来的正六边形重合，那么旋转的角度至少是　　度．‎ ‎　‎ 多边形与平面镶嵌 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．一个多边形的内角和是900°，则这个多边形的边数是（　　）‎ A．6 B．‎7 ‎C．8 D．9‎ ‎【考点】多边形内角与外角．‎ ‎【专题】计算题．‎ ‎【分析】本题根据多边形的内角和定理和多边形的内角和等于900°，列出方程，解出即可．‎ ‎【解答】解：设这个多边形的边数为n，‎ 则有（n﹣2）180°=900°，‎ 解得：n=7，‎ ‎∴这个多边形的边数为7．‎ 故选：B．‎ ‎【点评】本题主要考查多边形的内角和定理，解题的关键是根据已知等量关系列出方程从而解决问题．‎ ‎　‎ ‎2．若一个多边形的内角和为1080°，则这个多边形的边数为（　　）‎ A．6 B．‎7 ‎C．8 D．9‎ ‎【考点】多边形内角与外角．‎ ‎【分析】首先设这个多边形的边数为n，由n边形的内角和等于180°（n﹣2），即可得方程180（n﹣2）=1080，解此方程即可求得答案．‎ ‎【解答】解：设这个多边形的边数为n，‎ 根据题意得：180（n﹣2）=1080，‎ 解得：n=8．‎ 故选C．‎ ‎【点评】此题考查了多边形的内角和公式．此题比较简单，注意熟记公式是准确求解此题的关键，注意方程思想的应用．‎ ‎　‎ ‎3．正十边形的每个外角等于（　　）‎ A．18° B．36° C．45° D．60°‎ ‎【考点】多边形内角与外角．‎ ‎【专题】常规题型．‎ ‎【分析】根据正多边形的每一个外角等于多边形的外角和除以边数，计算即可得解．‎ ‎【解答】解：360°÷10=36°，‎ 所以，正十边形的每个外角等于36°．‎ 故选：B．‎ ‎【点评】本题考查了正多边形的外角和、边数、外角度数之间的关系，熟记正多边形三者之间的关系是解题的关键．‎ ‎　‎ ‎4．正六边形的每个内角都是（　　）‎ A．60° B．80° C．100° D．120°‎ ‎【考点】多边形内角与外角．‎ ‎【专题】常规题型．‎ ‎【分析】先利用多边形的内角和公式（n﹣2）•180°求出正六边形的内角和，然后除以6即可；‎ 或：先利用多边形的外角和除以正多边形的边数，求出每一个外角的度数，再根据相邻的内角与外角是邻补角列式计算．‎ ‎【解答】解：（6﹣2）•180°=720°，‎ 所以，正六边形的每个内角都是720°÷6=120°，‎ 或：360°÷6=60°，‎ ‎180°﹣60°=120°．‎ 故选D．‎ ‎【点评】本题考查了多边形的内角与外角，利用正多边形的外角度数、边数、外角和三者之间的关系求解是此类题目常用的方法，而且求解比较简便．‎ ‎　‎ ‎5．一个多边形的内角和与外角和相等，则这个多边形是（　　）‎ A．四边形 B．五边形 C．六边形 D．八边形 ‎【考点】多边形内角与外角．‎ ‎【分析】首先设此多边形是n边形，由多边形的外角和为360°，即可得方程180（n﹣2）=360，解此方程即可求得答案．‎ ‎【解答】解：设此多边形是n边形，‎ ‎∵多边形的外角和为360°，‎ ‎∴180（n﹣2）=360，‎ 解得：n=4．‎ ‎∴这个多边形是四边形．‎ 故选A．‎ ‎【点评】此题考查了多边形的内角和与外角和的知识．此题难度不大，注意多边形的外角和为360°，n边形的内角和等于180°（n﹣2）．‎ ‎　‎ ‎6．如果一个多边形的内角和是其外角和的一半，那么这个多边形是（　　）‎ A．六边形 B．五边形 C．四边形 D．三角形 ‎【考点】多边形内角与外角．‎ ‎【专题】应用题．‎ ‎【分析】任何多边形的外角和是360度，内角和等于外角和的一半则内角和是180度，可知此多边形为三角形．‎ ‎【解答】解：根据题意，得 ‎（n﹣2）•180°=180°，‎ 解得：n=3．‎ 故选D．‎ ‎【点评】本题主要考查了已知多边形的内角和求边数，可以转化为方程的问题来解决，难度适中．‎ ‎　‎ ‎7．一个正多边形的每个外角都等于36°，那么它是（　　）‎ A．正六边形 B．正八边形 C．正十边形 D．正十二边形 ‎【考点】多边形内角与外角．‎ ‎【分析】利用多边形的外角和360°，除以外角的度数，即可求得边数．‎ ‎【解答】解：360÷36=10．‎ 故选C．‎ ‎【点评】本题考查了多边形的外角和定理，理解任何多边形的外角和都是360度是关键．‎ ‎　‎ ‎8．只用下列图形中的一种，能够进行平面镶嵌的是（　　）‎ A．正十边形 B．正八边形 C．正六边形 D．正五边形 ‎【考点】平面镶嵌（密铺）．‎ ‎【分析】根据密铺的知识，找到一个内角能整除周角360°的正多边形即可．‎ ‎【解答】解：A、正十边形每个内角是180°﹣360°÷10=144°，不能整除360°，不能单独进行镶嵌，不符合题意；‎ B、正八边形每个内角是180°﹣360°÷8=135°，不能整除360°，不能单独进行镶嵌，不符合题意；‎ C、正六边形的每个内角是120°，能整除360°，能整除360°，可以单独进行镶嵌，符合题意；‎ D、正五边形每个内角是180°﹣360°÷5=108°，不能整除360°，不能单独进行镶嵌，不符合题意；‎ 故选：C．‎ ‎【点评】本题考查了平面密铺的知识，注意几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．‎ ‎　‎ ‎9．下列图形中，单独选用一种图形不能进行平面镶嵌的是（　　）‎ A．正三角形 B．正六边形 C．正方形 D．正五边形 ‎【考点】平面镶嵌（密铺）．‎ ‎【分析】几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．360°为正多边形一个内角的整数倍才能单独镶嵌．‎ ‎【解答】解：A、正三角形的一个内角度数为180﹣360÷3=60°，是360°的约数，能镶嵌平面，不符合题意；‎ B、正六边形的一个内角度数为180﹣360÷6=120°，是360°的约数，能镶嵌平面，不符合题意；‎ C、正方形的一个内角度数为180﹣360÷4=90°，是360°的约数，能镶嵌平面，不符合题意；‎ D、正五边形的一个内角度数为180﹣360÷5=108°，不是360°的约数，不能镶嵌平面，符合题意．‎ 故选：D．‎ ‎【点评】本题考查了平面密铺的知识，注意掌握只用一种正多边形镶嵌，只有正三角形，正四边形，正六边形三种正多边形能镶嵌成一个平面图案．‎ ‎　‎ ‎10．一个多边形截取一个角后，形成另一个多边形的内角和是1620°，则原来多边形的边数是（　　）‎ A．10 B．‎11 ‎C．12 D．以上都有可能 ‎【考点】多边形内角与外角．‎ ‎【专题】压轴题．‎ ‎【分析】首先计算截取一个角后多边形的边数，然后分三种情况讨论．因为截取一个角可能会多出一个角，也可能角的个数不变，也可能少一个角，从而得出结果．‎ ‎【解答】解：∵内角和是1620°的多边形是边形，‎ 又∵多边形截去一个角有三种情况．一种是从两个角的顶点截取，这样就少了一条边，即原多边形为12边形；‎ 另一种是从两个边的任意位置截，那样就多了一条边，即原多边形为10边形；‎ 还有一种就是从一个边的任意位置和一个角顶点截，那样原多边形边数不变，还是11边形．‎ 综上原来多边形的边数可能为10、11、12边形，‎ 故选D．‎ ‎【点评】本题主要考查了多边形的内角和定理及多边形截去一个角有三种情况．‎ ‎　‎ ‎11．如图，过正五边形ABCDE的顶点A作直线l∥BE，则∠1的度数为（　　）‎ A．30° B．36° C．38° D．45°‎ ‎【考点】平行线的性质；等腰三角形的性质；多边形内角与外角．‎ ‎【分析】首先根据多边形内角和计算公式计算出每一个内角的度数，再根据等腰三角形的性质计算出∠AEB，然后根据平行线的性质可得答案．‎ ‎【解答】解：∵ABCDE是正五边形，‎ ‎∴∠BAE=（5﹣2）×180°÷5=108°，‎ ‎∴∠AEB=（180°﹣108°）÷2=36°，‎ ‎∵l∥BE，‎ ‎∴∠1=36°，‎ 故选：B．‎ ‎【点评】此题主要考查了正多边形的内角和定理，以及三角形内角和定理，平行线的性质，关键是掌握多边形内角和定理：（n﹣2）．180° （n≥3）且n为整数．‎ ‎　‎ ‎12．如图，甲、乙两人想在正五边形ABCDE内部找一点P，使得四边形ABPE为平行四边形，其作法如下：‎ ‎（甲） 连接BD、CE，两线段相交于P点，则P即为所求 ‎（乙） 先取CD的中点M，再以A为圆心，AB长为半径画弧，交AM于P点，则P即为所求．‎ 对于甲、乙两人的作法，下列判断何者正确？（　　）‎ A．两人皆正确 B．两人皆错误 C．甲正确，乙错误 D．甲错误，乙正确 ‎【考点】平行四边形的判定．‎ ‎【分析】求出五边形的每个角的度数，求出∠ABP、∠AEP、∠BPE的度数，根据平行四边形的判定判断即可．‎ ‎【解答】‎ 解：甲正确，乙错误，‎ 理由是：如图，∵正五边形的每个内角的度数是=108°，AB=BC=CD=DE=AE，‎ ‎∴∠DEC=∠DCE=×（180°﹣108°）=36°，‎ 同理∠CBD=∠CDB=36°，‎ ‎∴∠ABP=∠AEP=108°﹣36°=72°，‎ ‎∴∠BPE=360°﹣108°﹣72°﹣72°=108°=∠A，‎ ‎∴四边形ABPE是平行四边形，即甲正确；‎ ‎∵∠BAE=108°，‎ ‎∴∠BAM=∠EAM=54°，‎ ‎∵AB=AE=AP，‎ ‎∴∠ABP=∠APB=×（180°﹣54°）=63°，∠AEP=∠APE=63°，‎ ‎∴∠BPE=360°﹣108°﹣63°﹣63°≠108°，‎ 即∠ABP=∠AEP，∠BAE≠∠BPE，‎ ‎∴四边形ABPE不是平行四边形，即乙错误；‎ 故选C．‎ ‎【点评】本题考查了正五边形的内角和定理，等腰三角形的性质，三角形的内角和定理，平行四边形的判定的应用，注意：有两组对角分别相等的四边形是平行四边形．‎ ‎　‎ ‎13．如图，小红做了一个实验，将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，所转过的度数是（　　）‎ A．60° B．72° C．108° D．120°‎ ‎【考点】旋转的性质；正多边形和圆．‎ ‎【分析】由六边形ABCDEF是正六边形，即可求得∠AFE的度数，又由邻补角的定义，求得∠E′FE的度数，由将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，可得∠EFE′是旋转角，继而求得答案．‎ ‎【解答】解：∵六边形ABCDEF是正六边形，‎ ‎∴∠AFE==120°，‎ ‎∴∠EFE′=180°﹣∠AFE=180°﹣120°=60°，‎ ‎∵将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，‎ ‎∴∠EFE′是旋转角，‎ ‎∴所转过的度数是60°．‎ 故选A．‎ ‎【点评】此题考查了正六边形的性质、旋转的性质以及旋转角的定义．此题难度不大，注意找到旋转角是解此题的关键．‎ ‎　‎ 二、填空题 ‎14．正n边形的一个外角的度数为60°，则n的值为　6　．‎ ‎【考点】多边形内角与外角．‎ ‎【专题】探究型．‎ ‎【分析】先根据正n边形的一个外角的度数为60°求出其内角的度数，再根据多边形的内角和公式解答即可．‎ ‎【解答】解：∵正n边形的一个外角的度数为60°，‎ ‎∴其内角的度数为：180°﹣60°=120°，‎ ‎∴=120°，解得n=6．‎ 故答案为：6．‎ ‎【点评】本题考查的是多边形的内角与外角，熟知多边形的内角和公式是解答此题的关键．‎ ‎　‎ ‎15．如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角．若∠A=120°，则∠1+∠2+∠3+∠4=　300°　．‎ ‎【考点】多边形内角与外角．‎ ‎【专题】数形结合．‎ ‎【分析】根据题意先求出∠5的度数，然后根据多边形的外角和为360°即可求出∠1+∠2+∠3+∠4的值．‎ ‎【解答】解：由题意得，∠5=180°﹣∠EAB=60°，‎ 又∵多边形的外角和为360°，‎ ‎∴∠1+∠2+∠3+∠4=360°﹣∠5=300°．‎ 故答案为：300°．‎ ‎【点评】本题考查了多边形的外角和等于360°的性质以及邻补角的和等于180°的性质，是基础题，比较简单．‎ ‎　‎ ‎16．△OAB是以正多边形相邻的两个顶点A，B与它的中心O为顶点的三角形，若△OAB的一个内角为70°，则该正多边形的边数为　9　．‎ ‎【考点】正多边形和圆．‎ ‎【分析】分∠OAB=70°和∠AOB=70°两种情况进行讨论即可求解．‎ ‎【解答】解：当∠OAB=70°时，∠AOB=40°，则多边形的边数是：360÷40=9；‎ 当∠AOB=70°时，360÷70结果不是整数，故不符合条件．‎ 故答案是：9．‎ ‎【点评】此题主要考查正多边形的计算问题，属于常规题．‎ ‎　‎ ‎17．一幅图案在某个顶点处由三个边长相等的正多边形镶嵌而成．其中的两个分别是正方形和正六边形，则第三个正多边形的边数是　12　．‎ ‎【考点】平面镶嵌（密铺）．‎ ‎【分析】正多边形的组合能否进行平面镶嵌，关键是看位于同一顶点处的几个角之和能否为360°．若能，则说明可以进行平面镶嵌；反之，则说明不能进行平面镶嵌．‎ ‎【解答】解：∵正方形的一个内角度数为180°﹣360°÷4=90°，正六边形的一个内角度数为180°﹣360°÷6=120°，‎ ‎∴需要的多边形的一个内角度数为360°﹣90°﹣120°=150°，‎ ‎∴需要的多边形的一个外角度数为180°﹣150°=30°，‎ ‎∴第三个正多边形的边数为360÷30=12．‎ 故答案为：12．‎ ‎【点评】此题主要考查了平面镶嵌，关键是掌握多边形镶嵌成平面图形的条件：同一顶点处的几个内角之和为360°；正多边形的边数为360÷一个外角的度数．‎ ‎　‎ ‎18．用4个全等的正八边形进行拼接，使相等的两个正八边形有一条公共边，围成一圈后中间形成一个正方形，如图1，用n个全等的正六边形按这种方式进行拼接，如图2，若围成一圈后中间形成一个正多边形，则n的值为　6　．‎ ‎【考点】平面镶嵌（密铺）．‎ ‎【专题】应用题；压轴题．‎ ‎【分析】根据正六边形的一个内角为120°，可求出正六边形密铺时需要的正多边形的内角，继而可求出这个正多边形的边数．‎ ‎【解答】解：两个正六边形结合，一个公共点处组成的角度为240°，‎ 故如果要密铺，则需要一个内角为120°的正多边形，‎ 而正六边形的内角为120°，‎ 故答案为：6．‎ ‎【点评】此题考查了平面密铺的知识，解答本题关键是求出在密铺条件下需要的正多边形的一个内角的度数，有一定难度．‎ ‎　‎ ‎19．如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=　240　度．‎ ‎【考点】多边形内角与外角．‎ ‎【专题】压轴题；数形结合．‎ ‎【分析】利用四边形的内角和得到∠B+∠C+∠D的度数，进而让五边形的内角和减去∠B+∠C+∠D的度数即为所求的度数．‎ ‎【解答】解：∵四边形的内角和为（4﹣2）×180°=360°，‎ ‎∴∠B+∠C+∠D=360°﹣60°=300°，‎ ‎∵五边形的内角和为（5﹣2）×180°=540°，‎ ‎∴∠1+∠2=540°﹣300°=240°，‎ 故答案为：240．‎ ‎【点评】考查多边形的内角和知识；求得∠B+∠C+∠D的度数是解决本题的突破点．‎ ‎　‎ ‎20．如图，六边形ABCDEF的六个内角都相等，若AB=1，BC=CD=3，DE=2，则这个六边形的周长等于　15　．‎ ‎【考点】等腰梯形的性质；多边形内角与外角；平行四边形的性质．‎ ‎【专题】计算题．‎ ‎【分析】凸六边形ABCDEF，并不是一规则的六边形，但六个角都是120°，所以通过适当的向外作延长线，可得到等边三角形，进而求解．‎ ‎【解答】解：如图，分别作直线AB、CD、EF的延长线和反向延长线使它们交于点G、H、P．‎ ‎∵六边形ABCDEF的六个角都是120°，‎ ‎∴六边形ABCDEF的每一个外角的度数都是60°．‎ ‎∴△AHF、△BGC、△DPE、△GHP都是等边三角形．‎ ‎∴GC=BC=3，DP=DE=2．‎ ‎∴GH=GP=GC+CD+DP=3+3+2=8，FA=HA=GH﹣AB﹣BG=8﹣1﹣3=4，EF=PH﹣HF﹣EP=8﹣4﹣2=2．‎ ‎∴六边形的周长为1+3+3+2+4+2=15．‎ 故答案为：15．‎ ‎【点评】本题考查了等边三角形的性质及判定定理；解题中巧妙地构造了等边三角形，从而求得周长．是非常完美的解题方法，注意学习并掌握．‎ ‎　‎ ‎21．如图，在正八边形ABCDEFGH中，四边形BCFG的面积为‎20cm2，则正八边形的面积为　‎40　cm2．‎ ‎【考点】正多边形和圆．‎ ‎【专题】压轴题．‎ ‎【分析】根据正八边形的性质得出正八边形每个内角以及表示出四边形ABGH面积进而求出答案即可．‎ ‎【解答】解：连接HE，AD，‎ 在正八边形ABCDEFGH中，可得：HE⊥BG于点M，AD⊥BG于点N，‎ ‎∵正八边形每个内角为： =135°，‎ ‎∴∠HGM=45°，‎ ‎∴MH=MG，‎ 设MH=MG=x，‎ 则HG=AH=AB=GF=x，‎ ‎∴BG×GF=2（+1）x2=20，‎ 四边形ABGH面积=（AH+BG）×HM=（+1）x2=10，‎ ‎∴正八边形的面积为：10×2+20=40（cm2）．‎ 故答案为：40．‎ ‎【点评】此题主要考查了正八边形的性质以及勾股定理等知识，根据已知得出四边形ABGH面积是解题关键．‎ ‎　‎ ‎22．如图，由7个形状、大小完全相同的正六边形组成网格，正六边形的顶点称为格点．已知每个正六边形的边长为1，△ABC的顶点都在格点上，则△ABC的面积是　2　．‎ ‎【考点】正多边形和圆．‎ ‎【专题】压轴题．‎ ‎【分析】延长AB，然后作出过点C与格点所在的直线，一定交于格点E，根据S△ABC=S△AEC﹣S△BEC即可求解．‎ ‎【解答】解：延长AB，然后作出过点C与格点所在的直线，一定交于格点E．‎ 正六边形的边长为1，则半径是1，则CE=4，‎ 中间间隔一个顶点的两个顶点之间的距离是：，则△BCE的边EC上的高是：，‎ ‎△ACE边EC上的高是：，‎ 则S△ABC=S△AEC﹣S△BEC=×4×（﹣）=2．‎ 故答案是：2．‎ ‎【点评】本题考查了正多边形的计算，正确理解S△ABC=S△AEC﹣S△BEC是关键．‎ ‎　‎ ‎23．如图，正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置．若正六边形的边长为‎2cm，则正六边形的中心O运动的路程为　4π　cm．‎ ‎【考点】正多边形和圆；弧长的计算；旋转的性质．‎ ‎【分析】每次滚动正六边形的中心就以正六边形的半径为半径旋转60°，然后计算出弧长，最后乘以六即可得到答案．‎ ‎【解答】解：根据题意得：每次滚动正六边形的中心就以正六边形的半径为半径旋转60°，‎ 正六边形的中心O运动的路程∵正六边形的边长为‎2cm，‎ ‎∴运动的路径为： =；‎ ‎∵从图1运动到图2共重复进行了六次上述的移动，‎ ‎∴正六边形的中心O运动的路程6×=4πcm 故答案为：4π．‎ ‎【点评】本题考查了正多边形和圆的、弧长的计算及旋转的性质，解题的关键是弄清正六边形的中心运动的路径．‎ ‎　‎ ‎24．如图，将正六边形绕其对称中心O旋转后，恰好能与原来的正六边形重合，那么旋转的角度至少是　60　度．‎ ‎【考点】旋转对称图形．‎ ‎【分析】本题考查旋转对称图形的概念，旋转的最小度数是解决本题的关键．‎ ‎【解答】解：将正六边形绕其对称中心O旋转后，恰好能与原来的正六边形重合，那么旋转的角度至少是=60度．‎ ‎【点评】根据旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．‎