中考数学一轮复习 专题练习7 平面几何基础2 浙教版 27页

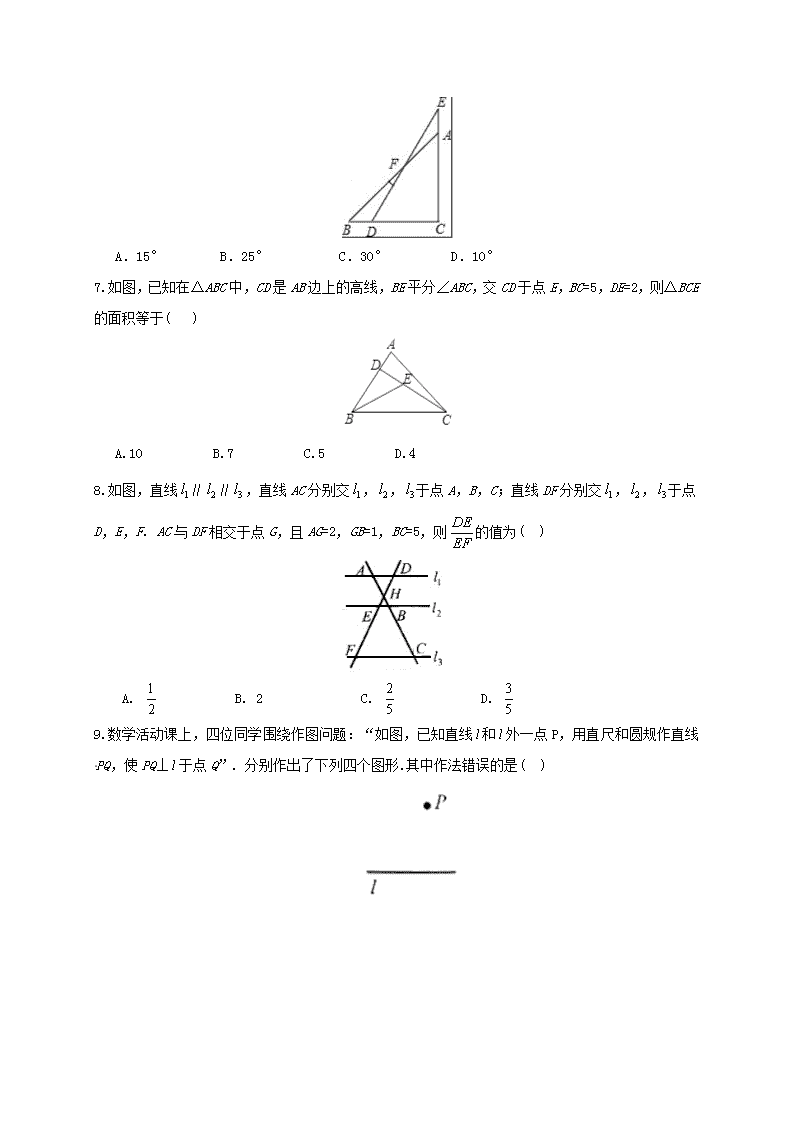
平面几何基础（2）‎ 班级 姓名 学号 ‎ 一、选择题 ‎1.下列图形中，既是轴对称图形，又是中心对称图形的是（ ） ‎ ‎ A. 等边三角形 B. 平行四边形 ‎ ‎ C. 等腰梯形 D. 圆 ‎2.下列命题中的真命题是（ ）‎ A. 关于中心对称的两个图形全等 B. 全等的两个图形是中心对称图形 ‎ C. 中心对称图形都是轴对称图形 D. 轴对称图形都是中心对称图形 ‎3.边长为的正六边形的面积等于（ ） ‎ A． B． C． D．‎ ‎4.下列图形中，既可以看作是轴对称图形，又可以看作是中心对称图形的为（ ）‎ A. B. C. D. ‎ ‎5.如图，AB、CD相交于点O，∠1=80°，如果DE∥AB，那么∠D的度数为（ ）‎ A. 80° B. 90° C. 100° D. 110°‎ ‎6.如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（ ）‎ A．15° B．25° C．30° D．10°‎ ‎7.如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于( )‎ A.10 B‎.7 C.5 D.4‎ ‎8.如图，直线∥∥，直线AC分别交，，于点A，B，C；直线DF分别交，，于点D，E，F. AC与DF相交于点G，且AG=2，GB=1，BC=5，则的值为( )‎ A. B. ‎2 C. D. ‎ ‎9.数学活动课上，四位同学围绕作图问题：“如图，已知直线和外一点P，用直尺和圆规作直线PQ，使PQ⊥于点Q”. 分别作出了下列四个图形.其中作法错误的是( )‎ A.B.C. D. 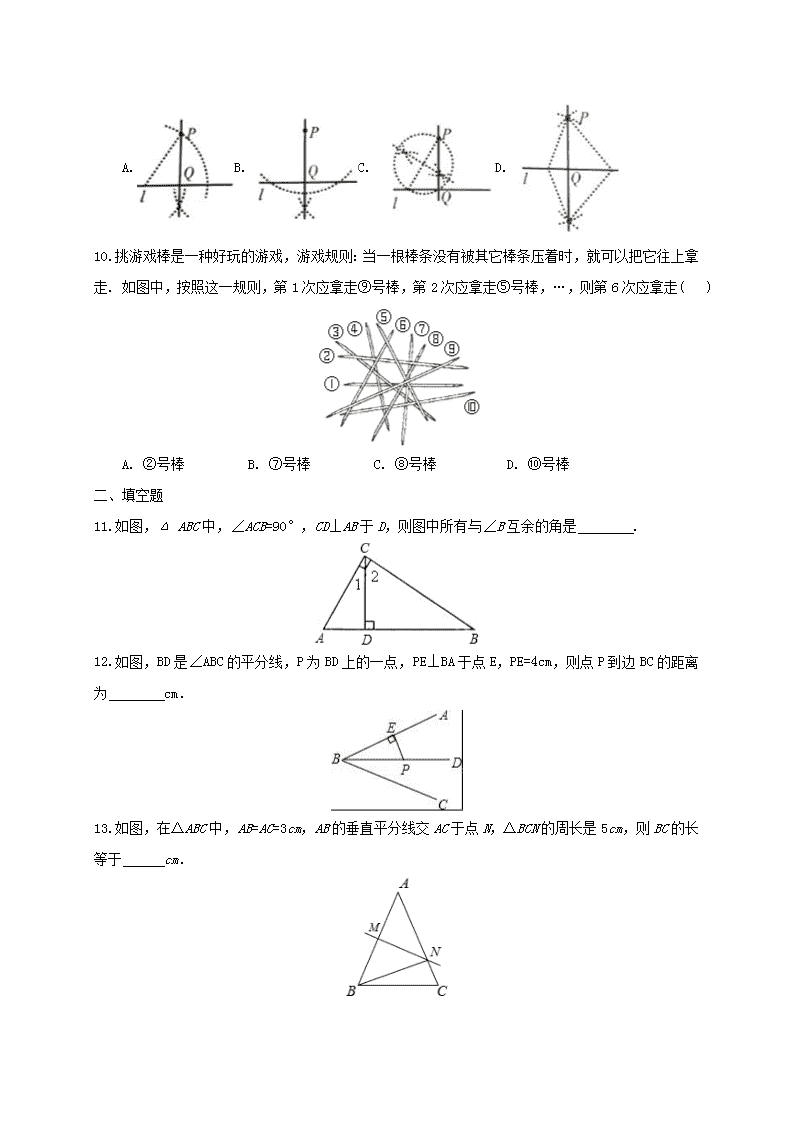‎ ‎10.挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走. 如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走( )‎ A. ②号棒 B. ⑦号棒 C. ⑧号棒 D. ⑩号棒 二、填空题 ‎11.如图，Δ ABC中，∠ACB=90°，CD⊥AB于D，则图中所有与∠B互余的角是 .‎ ‎12.如图，BD是∠ABC的平分线，P为BD上的一点，PE⊥BA于点E，PE=‎4cm，则点P到边BC的距离为　 　cm．‎ ‎13.如图，在△ABC中，AB=AC=‎3cm，AB的垂直平分线交AC于点N，△BCN的周长是‎5cm，则BC的长等于　 cm．‎ ‎14.如图，直线是一组等距离的平行线，过直线上的点A作两条射线，分别与直线，相交于点B，E，C，F. 若BC=2，则EF的长是 ‎ ‎15.如图，直线a∥b，△ABC是等边三角形，点A在直线a上，边BC在直线b上，把△ABC沿BC方向平移BC的一半得到△A′B′C′（如图①）；继续以上的平移得到图②，再继续以上的平移得到图③，…；请问在第100个图形中等边三角形的个数是 　．‎ 三、解答题 ‎ 16.在平面直角坐标系中，已知ABC的三个顶点的坐标分别为A（－1,1）， B （-3,1）， C（-1,4）．‎ （1） 画出△ABC关于y轴对称的；‎ （2） 将△ABC绕着点B顺时针旋转90°后得到△A2BC2，请在图中画出△A2BC2，并求出线段BC旋转过程中所扫过的面积（结果保留）.‎ ‎ ‎ ‎17.“综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度 ‎（1）用记号(a，b，c)(a≤b≤c)表示一个满足条件的三角形，如(2，3，3)表示边长分别为2，3，3个单位长度的一个三角形，请列举出所有满足条件的三角形；‎ ‎（2）用直尺和圆规作出三边满足aDE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点；‎ ‎（3）已知点C是线段AB上的一定点，其位置如图3所示，请在BC上画一点D，使C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画出一种情形即可）；‎ ‎（4）如图4，已知点M，N是线段AB的勾股分割点，MN>AM≥BN，△AMC，△MND和△NBM均是等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究，和的数量关系，并说明理由.‎ 答案详解 一、选择题 ‎【答案】A。‎ ‎【考点】命题与定理，中心对称图形，轴对称图形。‎ ‎【分析】根据轴对称图形与中心对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合；中心对称图形是图形沿对称中心旋转180度后与原图重合。因此，‎ A、关于中心对称的两个图形全等，故正确；‎ B、全等的两个图形不一定是中心对称图形，故错误；‎ C、中心对称图形不一定是轴对称图形，故错误；‎ D、轴对称图形不一定是中心对称图形，故错误。‎ 故选A。‎ ‎3.边长为的正六边形的面积等于（ ） ‎ A． B． C． D．‎ ‎【答案】C。‎ ‎【考点】正多边形。‎ ‎【分析】边长为的正六边形的面积=6×边长为的等边三角形的面积=6×××（×sin60°）=。故选C。‎ ‎4.下列图形中，既可以看作是轴对称图形，又可以看作是中心对称图形的为（ ）‎ A. B. C. D. ‎ ‎【答案】B。‎ ‎【考点】中心对称图形，轴对称图形。‎ ‎【分析】 根据轴对称图形与中心对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合；中心对称图形是图形沿对称中心旋转180度后与原图重合。因此，‎ A、是轴对称图形，不是中心对称图形，不符合题意；‎ B、是轴对称图形，也是中心对称图形，符合题意；‎ C、是轴对称图形，不是中心对称图形，不符合题意；‎ D、不是轴对称图形，也不是中心对称图形，不符合题意。‎ ‎ 故选B。‎ ‎5.如图，AB、CD相交于点O，∠1=80°，如果DE∥AB，那么∠D的度数为（ ）‎ A. 80° B. 90° C. 100° D. 110°‎ ‎【答案】B。‎ ‎【考点】平行线的性质，对顶角的性质。‎ ‎【分析】∵∠1=80°，∴∠BOD=∠1=80°。‎ ‎∵DE∥AB，∴∠D=180－∠BOD=100°。‎ 故选B。‎ ‎6.如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（ ）‎ A．15° B．25° C．30° D．10°‎ ‎【答案】A。‎ ‎【考点】三角形的外角性质，三角形内角和定理。‎ ‎【分析】∵Rt△CDE中，∠C=90°，∠E=30°，∴∠BDF=∠C+∠E=90°+30°=120°。‎ ‎∵△BDF中，∠B=45°，∠BDF=120°，∴∠BFD=180°﹣45°﹣120°=15°。‎ 故选A。　‎ ‎7.如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于( )‎ A.10 B‎.7 C.5 D.4‎ ‎【答案】C.‎ ‎【考点】角平分线的性质；三角形面积的计算.‎ ‎【分析】如答图，过点作于点，‎ ‎∵CD是AB边上的高线，∴.‎ ‎∵BE平分∠ABC，DE=2，∴.‎ ‎∵BC=5，∴.‎ 故选C.‎ ‎8.如图，直线∥∥，直线AC分别交，，于点A，B，C；直线DF分别交，，于点D，E，F. AC与DF相交于点G，且AG=2，GB=1，BC=5，则的值为( )‎ A. B. ‎2 C. D. ‎ ‎【答案】D.‎ ‎【考点】平行线分线段成比例的性质.‎ ‎【分析】∵AG=2，GB=1，BC=5，∴.‎ ‎∵直线∥∥，∴.‎ 故选D.‎ ‎9.数学活动课上，四位同学围绕作图问题：“如图，已知直线和外一点P，用直尺和圆规作直线PQ，使PQ⊥于点Q”. 分别作出了下列四个图形.其中作法错误的是( )‎ A. B. C. D. ‎ ‎【答案】A.‎ ‎【考点】尺规作图.‎ ‎【分析】根据垂线的作法，选项A错误. 故选A.‎ ‎10.挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走. 如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走( )‎ A. ②号棒 B. ⑦号棒 C. ⑧号棒 D. ⑩号棒 ‎【答案】D.‎ ‎【考点】探索规律题（图形变化类）.‎ ‎【分析】当一根棒条没有被其它棒条压着时，就可以把它往上拿走. 如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，第3次应拿走⑥号棒，第4次应拿走②号棒，第5次应拿走⑧号棒，第6次应拿走⑩号棒，故选D.‎ 二、填空题 ‎11.如图，ΔABC中，∠ACB=90°，CD⊥AB于D，则图中所有与∠B互余的角是 .‎ ‎【答案】∠A和∠2。‎ ‎【考点】直角三角形两锐角的关系，余角定义。‎ ‎【分析】利用“直角三角形两锐角之和为90°”的性质来解题：‎ ‎∵∠ACB=90°，∴∠A+∠B=90°。‎ 又∵CD⊥AB于D，∴∠2+∠B=90°。根据互余定义，与∠B互余的角为∠A和∠2。‎ ‎12.如图，BD是∠ABC的平分线，P为BD上的一点，PE⊥BA于点E，PE=‎4cm，则点P到边BC的距离为　 　cm．‎ ‎【答案】4。‎ ‎【考点】角平分线的性质。‎ ‎【分析】∵BD是∠ABC的平分线，PE⊥AB于点E，PE=‎4cm，‎ ‎∴根据角平分线上的点到角的两边相等垢性质，点P到BC的距离=PE=‎4cm。　‎ ‎13.如图，在△ABC中，AB=AC=‎3cm，AB的垂直平分线交AC于点N，△BCN的周长是‎5cm，则BC的长等于　 cm．‎ ‎【答案】2。‎ ‎【考点】线段垂直平分线的性质。‎ ‎【分析】∵AB的垂直平分线交AC于点N，∴NA=NB。‎ 又∵△BCN的周长是‎5cm，∴BC+BN+NC=‎5cm。∴BC+AN+NC=‎5cm。‎ 而AC=AN+NC=‎3cm，∴BC=‎2cm。‎ ‎14.如图，直线是一组等距离的平行线，过直线上的点A作两条射线，分别与直线，相交于点B，E，C，F. 若BC=2，则EF的长是 ‎ ‎【答案】5.‎ ‎【考点】平行线分线段成比例的性质；相似三角形的判定和性质.‎ ‎【分析】∵直线是一组等距离的平行线，∴，即.‎ 又∵∥，∴. ∴.‎ ‎∵BC=2，∴.‎ ‎15.如图，直线a∥b，△ABC是等边三角形，点A在直线a上，边BC在直线b上，把△ABC沿BC方向平移BC的一半得到△A′B′C′（如图①）；继续以上的平移得到图②，再继续以上的平移得到图③，…；请问在第100个图形中等边三角形的个数是　301　．‎ ‎【解析】如图①‎ ‎∵△ABC是等边三角形，‎ ‎∴AB=BC=AC，‎ ‎∵A′B′∥AB，BB′=B′C=BC，‎ ‎∴B′O=AB，CO=AC，‎ ‎∴△B′OC是等边三角形，同理阴影的三角形都是等边三角形．‎ 又观察图可得，第1个图形中大等边三角形有2个，小等边三角形有2个，‎ 第2个图形中大等边三角形有3个，小等边三角形有4个，‎ 第3个图形中大等边三角形有4个，小等边三角形有6个，…‎ 依次可得第n个图形中大等边三角形有n+1个，小等边三角形有2n个．‎ 故第100个图形中等边三角形的个数是：100+1+2×100=301．‎ 故答案为：301．‎ 三、 解答题 ‎16.在平面直角坐标系中，已知ABC的三个顶点的坐标分别为A（－1,1），B（-3,1），C（-1,4）．‎ （1） 画出△ABC关于y轴对称的；‎ （2） 将△ABC绕着点B顺时针旋转90°后得到△A2BC2，请在图中画出△A2BC2，并求出线段BC旋转过程中所扫过的面积（结果保留）.‎ ‎【解析】‎ ‎（1）如图所示，画出△ABC关于y轴对称的△A1B‎1C1；‎ ‎（2）如图所示，画出△ABC绕着点B顺时针旋转90°后得到△A2BC2，‎ 线段BC旋转过程中所扫过得面积S==．‎ ‎17.“综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度 ‎（1）用记号(a，b，c)(a≤b≤c)表示一个满足条件的三角形，如(2，3，3)表示边长分别为2，3，3个单位长度的一个三角形，请列举出所有满足条件的三角形；‎ ‎（2）用直尺和圆规作出三边满足aDE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点；‎ ‎（3）已知点C是线段AB上的一定点，其位置如图3所示，请在BC上画一点D，使C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画出一种情形即可）；‎ ‎（4）如图4，已知点M，N是线段AB的勾股分割点，MN>AM≥BN，△AMC，△MND和△NBM均是等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究，和的数量关系，并说明理由.‎ ‎【答案】解：（1）∵点M，N是线段AB的勾股分割点， AM=2，MN=3，‎ ‎∴若MN为斜边，则，即，解得.‎ 若BN为斜边，则，即，解得.‎ ‎∴BN的长为或.‎ ‎（2）证明：∵点D，E是线段BC的勾股分割点，且EC>DE≥BD，‎ ‎∴.‎ ‎∵在△ABC中，FG是中位线，AD，AE分别交FG于点M，N，‎ ‎∴FM、MN、NG分别是△ABD、△ADE、△AEC的中位线.‎ ‎∴BD=2FM，DE=2MN，EC=2NG.‎ ‎∴，即.‎ ‎∴.‎ ‎∴点M，N是线段FG的勾股分割点.‎ ‎（3）如答图1，C，D是线段AB的勾股分割点.‎ ‎（4）.理由如下：‎ 设，，，‎ ‎∵是的中点，∴.‎ ‎∵△，△均为等边三角形，∴.‎ ‎∵，∴△≌△.∴.∴.‎ ‎∵，∴△∽△.‎ ‎∴.∴.‎ ‎∵点，是线段的勾股分割点，∴.∴，‎ 又∵.∴. ‎ 在△和△中，，，，‎ ‎∴△≌△.‎ ‎∴.‎ ‎∵，∴.‎ ‎∴.‎ ‎∵，，‎ ‎∴.‎