中考数学考前冲刺最后一讲开放型问题解题指导 19页

‎ 2010中考数学考前冲刺最后一讲------开放型问题解题指导 2010-6-11‎ 一、课标下复习指南 传统的解答题和证明题，其条件和结论都是由题目明确给出的，我们的工作就是由因导果或执果索因．而探究性问题一般没有明确的条件或结论，没有固定的形式和方法，要求我们认真收集和处理问题的信息，通过观察、分析、综合、归纳、概括、猜想和论证等深层次的探索活动，认真研究才能得到问题的解答．开放性、操作性、探索性和综合性是探究性问题的明显特征．这类题目形式新颖，格调清新，涉及的基础知识和基本技能十分广泛，解题过程中有较多的创造性和探索性，解答方法灵活多变，既需要扎实的基础知识和基本技能，具备一定的数学能力，又需要思维的创造性和具有良好的个性品质．‎ 二、例题分析 ‎1．探究规律 对于探究规律的问题，需要认真审题，对题目提供的素材要进行观察、分析、综合，既要从素材的单个元素(如某个式子、图形)的各部分观察其相互关系，也要从素材的一系列元素(如一系列的式子、图形)之间观察其运动变化规律(如什么变化了，什么没有变等等)．其中更多地用到归纳与类比的方法，把具体与抽象、静止与运动结合起来，先猜想出结论，然后再从理论上加以证明．‎ 例1 观察下列各式：，…想一想，什么样的两数之积等于这两数之和?设n表示正整数，用关于n的等式表示这个规律．‎ 分析 所给各式中的两个数中，一个是分数，一个是整数，且分数的分子比分母大1，分子与整数相等，因此得到规律：‎ ‎(n为正整数)‎ 这个规律是否正确呢?可将等式左右两边分别化简，即能得出结论．请同学们自己完成．‎ 说明 对于“数字规律”的观察，要善于发现其中的变量与不变量，以及变量与项数之间的关系，将规律用代数式表示出来．‎ 对于所猜规律是否正确要有检验的意识，如在本题中把规律表示成 ‎(n为正整数)就是错误的，这是由于n＝1时，用上式表示的等式不符合已知中的第一项“1”这种情形．‎ 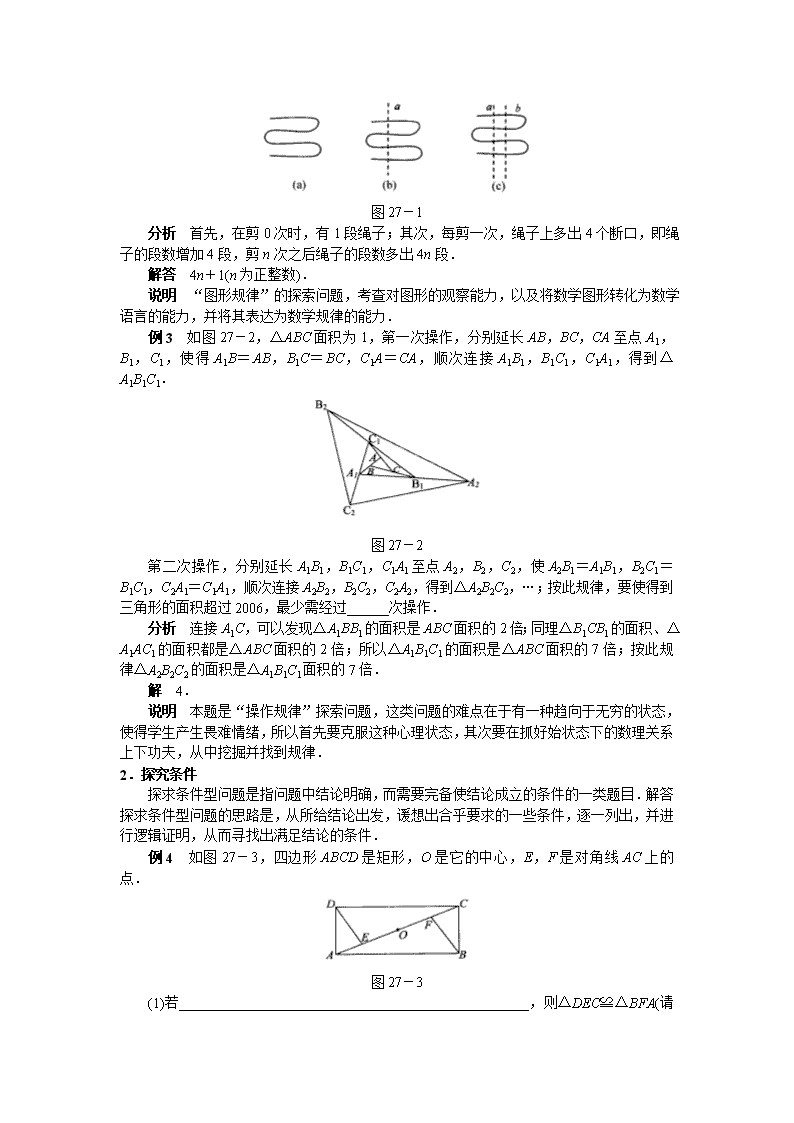例2 一根绳子，弯曲成如图27－1(a)所示的形状，当用剪刀像图(b)那样沿虚线a把绳子剪断时，绳子被剪为5段；当用剪刀像图(c)那样沿虚线b(b∥a)把绳子再剪一次时，绳子被剪为9段，当用剪刀在虚线a，b之间把绳子再剪(n－2)次(剪刀的方向与a平行)，这样一共剪n次时，绳子的段数是____________ (用含n的代数式表示)．‎ 图27－1‎ 分析 首先，在剪0次时，有1段绳子；其次，每剪一次，绳子上多出4个断口，即绳子的段数增加4段，剪n次之后绳子的段数多出4n段．‎ 解答 4n＋1(n为正整数)．‎ 说明 “图形规律”的探索问题，考查对图形的观察能力，以及将数学图形转化为数学语言的能力，并将其表达为数学规律的能力．‎ 例3 如图27－2，△ABC面积为1，第一次操作，分别延长AB，BC，CA至点A1，B1，C1，使得A1B＝AB，B1C＝BC，C1A＝CA，顺次连接A1B1，B1C1，C1A1，得到△A1B1C1．‎ 图27－2‎ 第二次操作，分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1＝A1B1，B2C1＝B1C1，C2A1＝C1A1，顺次连接A2B2，B2C2，C2A2，得到△A2B2C2，…；按此规律，要使得到三角形的面积超过2006，最少需经过______次操作．‎ 分析 连接A1C，可以发现△A1BB1的面积是ABC面积的2倍；同理△B1CB1的面积、△A1AC1的面积都是△ABC面积的2倍；所以△A1B1C1的面积是△ABC面积的7倍；按此规律△A2B2C2的面积是△A1B1C1面积的7倍．‎ 解 4．‎ 说明 本题是“操作规律”探索问题，这类问题的难点在于有一种趋向于无穷的状态，使得学生产生畏难情绪，所以首先要克服这种心理状态，其次要在抓好始状态下的数理关系上下功夫，从中挖掘并找到规律．‎ ‎2．探究条件 探求条件型问题是指问题中结论明确，而需要完备使结论成立的条件的一类题目．解答探求条件型问题的思路是，从所给结论出发，谖想出合乎要求的一些条件，逐一列出，并进行逻辑证明，从而寻找出满足结论的条件．‎ 例4 如图27－3，四边形ABCD是矩形，O是它的中心，E，F是对角线AC上的点．‎ 图27－3‎ ‎(1)若__________________________________________________，则△DEC≌△BFA ‎(请你填上能使结论成立的一个条件)；‎ ‎(2)证明你的结论．‎ 解 (1)AE＝CF；(OE＝OF；DE⊥AC，BF⊥AC；DE∥BF等等)‎ ‎(2)以AE＝CF为例．∵四边形ABCD是矩形，∴AB＝CD，AB∥CD，∠DCE＝∠BAF．‎ 又∵AE＝CF．∴AC－AE＝AC－CF．∴AF＝CE，∴△DEC≌△BAF．‎ 说明 这是一道探索条件、补充条件的开放型试题，解决这类问题的一般方法是：从结论出发，执果寻因，逆向推理，探寻出使结论成立的条件；有时也采取把可能产生结论的条件一一列出，逐个分析考察．‎ 例5 在平面直角坐标系中，等腰三角形ABC的顶点A的坐标为(2，2)．‎ ‎(1)若底边BC在x蚰上，请写出一组满足条件的点B，点C的坐标：____________；设点B，点C的坐标分别为(m，0)，(n，0)，你认为m，n应满足怎样的条件?‎ ‎(2)若底边BC的两个端嬴分别在x轴，y轴上，请写出一组满足条件的点B，点C的坐标：________________________；设点B，点C的坐标分别为(m，0)，(0，n)，你认为m，n应满足怎样的条件?‎ 分析 可以通过等腰三角形的作法来探求符合题意的条件：由于AB＝AC，故点B和点C在以A为圆心的同一个圆上．(1)如图27－4(a)，作AE⊥x轴于E，以大于AE的长度为半径画弧，与x轴的交点即为符合题意的点B和点C．易知E(2，0)为线段BC的中点，故CE＝EB，即n－2＝2－m；(2)类似于(1)作⊙A，与两条坐标轴分别交于B1，B2，C1，C2，显然当A，B，C三点不共线时这样确定的点B，C均符合题意．‎ 图27－4‎ 解 (1)如：点B(0，0)，点C(4，0)；m＋n＝4且m≠n．‎ ‎(2)如：点B(1，0)，点C(0，1)，或点B(3，0)，点C(0，1)；m＝n，且m，n不为0和4；或m＋n＝4．‎ 例6 如图27－5，AB，AC分别是⊙O的直径和弦，D为劣弧上一点，DE⊥AB于点H，交⊙O于点E，交AC于点F，P为ED的延长线一点．‎ 图27－5‎ ‎(1)当△PCF满足什么条件时，PC与⊙O相切?为什么?‎ ‎(2)点D在劣弧的什么位置时，才能使AD2＝DE·DF?为什么?‎ 分析 (1)连接OC．要使PC与⊙O相切，则只需∠PCO＝90°即可．由∠OCA＝∠OAC，∠PFC＝∠AFH，即可寻找出△PCF所要满足的条件；(2)要使AD2＝DE·DF，即，也就是要使△DAF∽△DEA，这样问题就较容易解决了．‎ 解 (1)当PC＝PF(或∠PCF＝∠PFC，或△PCF是等边三角形)时，PC与⊙O相切．证明：连接OC．∵PC＝PF，∴∠PCF＝∠PFC．‎ ‎∴∠PCO＝∠PCF＋∠OCA＝∠PFC＋∠OAC＝∠AFH＋∠AHF＝90°．‎ ‎∴PC与⊙O相切．‎ ‎(2)当点D是的中点时，AD2＝DE·DF．‎ 连接AE，∵＝，∴∠DAF＝∠DEA．‎ 又∴∠ADF＝∠EDA．∴△DAF∽△DEA．‎ ‎，∴AD2＝DE·DF．‎ 说明 本题是探索条件开放题，在解决这类问题时，我们常从要获得的结论出发来探求该结论成立的条件．如第(1)小题中，若要PC与⊙O相切，则我们需要怎样的条件；第(2)小题也是如此．‎ ‎3．探究结论 探求结论型问题是指由给定的已知条件探求相应的结论的一类问题．比如结论开放，不确定或不唯一，需要探求多个结论的问题；又如探求条件在一定范围内变化，图形在一定范围内运动，结论的不变性问题；再如探究图形的位置关系，数值的大小关系，猜想新结论等问题．解答这类问题的思路是：从所给条件(包括图形特征)出发，进行探索、归纳，大胆猜想出结论，然后对猜想的结论进行推理、证明．‎ 对于结论开放的探索性问题，答案不唯一．寻找结论的关键是抓住命题的条件及其特点(尤其是利用特殊几何图形的判定和性质)，寻找相等关系、特殊图形、两图形的关系等．‎ 例7 已知：如图27－6(a)，Rt△ABC≌Rt△ADE，∠ABC＝∠ADE＝90°，试以图中标有字母的点为端点，连接两条线段，如果你所连接的两条线段满足相等、垂直或平行关系中的一种，那么请你把它写出来并证明．‎ 图27－6(a)‎ 解 可以写出的结论有：CD＝BE，DB∥CE，AF⊥BD，AF⊥CE等．‎ ‎(1)如图27－6(b)，连接CD，BE，得CD＝BE．‎ 图27－6(b)‎ 证明：∵△ABC≌△ADE，‎ ‎∴AB＝AD，AC＝AE．‎ 又∠CAB＝∠EAD，∴∠CAD＝∠EAB．‎ ‎∴△ADC≌△ABE．∴CD＝BE．‎ ‎(2)如图27－6(c)，连接DB，CE，得DB∥CE．‎ 图27－6(c)‎ 证明：∵△ABC≌△ADE，∴AD＝AB．‎ ‎∴∠ADB＝∠ABD．‎ ‎∵∠ABC＝∠ADE，∴∠BDF＝∠FBD．‎ 由AC＝AE可得∠ACE＝∠AEC．‎ ‎∵∠ACB＝∠AED，∴∠FCE＝∠FEC．‎ ‎∵∠BDF＋∠FBD＝∠FCE＋∠FEC，‎ ‎∴∠FCE＝∠DBF．‎ ‎∴DB∥CE．‎ ‎(3)如图27－6(d)，连接DB，AF，得AF⊥BD．‎ 图27－6(d)‎ ‎∵△ABC≌△ADE，‎ ‎∴AD＝AB，∠ABC＝∠ADE＝90°．‎ 又∵AF＝AF，∴△ADF≌△ABF．‎ ‎∴∠DAF＝∠BAF．∴AF⊥BD．‎ ‎(4)如图27－6(e)，连接CE、AF，得AF⊥CE．‎ 图27－6(e)‎ 同(3)得∠DAF＝∠BAF．‎ 可得∠CAF＝∠EAF．‎ ‎∴AF⊥BD．‎ 例8 已知：在Rt△ABC中，∠ABC＝90°，D是AC的中点，⊙O经过A，D，B三点，CB的延长线交⊙O于点E(如图27－7(a))．‎ 在满足上述条件的情况下，当∠CAB 的大小变化时，图形也随着改变(如图(b))，在这个变化过程中，有些线段总保持着相等的关系．‎ ‎(1)观察上述图形，连接图(b)中已标明字母的某两点，得到一条新线段，证明它与线段CE相等；‎ 图27－7‎ ‎(2)在图27－7(b)中，过点E作⊙O的切线，交AC的延长线于点F．‎ ‎①若CF＝CD，求sin∠CAB的值；‎ ‎②若(n＞0)，试用含n的代数式表示sin∠CAB(直接写出结果)．‎ 解 (1)连接AE．求证：AE＝CE．‎ 证法一：如图27－8(a)，连接OD．‎ 图27－8‎ ‎∵∠ABC＝90°，CB的延长线交⊙O于点E，‎ ‎∴∠ABE＝90°．‎ ‎∴AE是⊙O的直径．‎ ‎∵D是AC的中点，O是AE的中点，‎ ‎∵‎ ‎∴AE＝CE．‎ 证法二：如图27－8(b)，连接DE．同证法一，得AE是⊙O的直径．‎ ‎∴∠ADE＝90°．‎ ‎∵D是AC的中点，‎ ‎∴DE是线段AC的垂直平分线．‎ ‎∴AE＝CE．‎ ‎(2)①根据题意画出图形．如图27－8(c)，连接DE．∵AE是⊙O的直径，EF是⊙O的切线，‎ ‎∴∠ADE＝∠AEF＝90°．‎ ‎∴Rt△ADE∽Rt△EDF．‎ 设AD＝k(k＞0)，则 DF＝2k．‎ 在Rt△CDE中，∵CE2＝CD2＋DE2＝3k2，‎ ‎∵∠CAB＝∠DEC，‎ ‎②‎ 说明 解决探究结论性问题，要注意充分挖掘题设的信息，顺向推理，或联想类比从而获得结论．‎ ‎4．存在性问题 探求存在性问题是指在一定条件下，判断某种数学对象是否存在的问题，它有结论存在和结论不存在两种情形．解答这类问题，一般先对结论作肯定存在的假设，然后由此肯定的假设出发，结合已知条件进行推理论证，若导出矛盾，则否定先前假设；若推出合理的结论，则说明假设正确，由此得出问题的结论．‎ 例9 如图27－9(a)，梯形ABCD中，AD∥BC，∠ABC＝90°，AD＝9，BC＝12，AB＝a，在线段BC上任取一点P(P不与B，C重合)，连接DP，作射线PE⊥DP，PE与直线AB交于点E．‎ 图27－9(a)‎ ‎(1)试确定CP＝3时，点E的位置；‎ ‎(2)若设CP＝x(x＞0)，BE＝y(y＞0)，试写出y关于自变量x的函数关系式；‎ ‎(3)若在线段BC上能找到不同的两点P1，P2，使按上述作法得到的点E都与点A重合，试求出此时a的取值范围．‎ 图27－9(b)‎ 解 (1)作DF⊥BC，F为垂足．‎ 当CP＝3时，四边形ADFB是矩形，则CF＝3．‎ ‎∴点P与点F重合．‎ 又∵BF⊥FD，‎ ‎∴此时点E与点B重合．‎ ‎(2)(i)当点P在BF上(不与B，F重合)时，(见图27－9(a))‎ ‎∵∠EPB＋∠DPF＝90°，∠EPB＋∠PEB＝90°，‎ ‎∴∠DPF＝∠PEB．‎ ‎∴Rt△PEB∽△Rt△DPF．‎ ‎ ①‎ 又∵BE＝y，BP＝12－x，FP＝x－3，FD＝a，代入①式，得 ‎，整理，‎ 得 ②‎ ‎(ii)当点P在CF上(不与C，F重合)时，(见图27－9(b))同理可求得．由FP＝3－x得 ‎(3)解法一：当点E与A重合时，y＝EB＝a，此时点P在线段BF上．由②式得15x＋36)．‎ 整理得x2－15x＋36＋a2＝0． ③‎ ‎∵在线段BC上能找到两个不同的点P1与P2满足条件，‎ ‎∴方程③有两个不相等的正实根．‎ ‎∴D＝(－15)2－4×(36＋a2)＞0．‎ 解得 又∵a＞0，‎ 解法二：当点E与A重合时，‎ ‎∵∠APD＝90°，‎ ‎∴点P在以AD为直径的圆上．设圆心为M，则M为AD的中点．‎ ‎∵在线段BC上能找到两个不同的点P1与P2满足条件，‎ ‎∴线段BC与⊙M相交．即圆心M到BC的距离d满足 ④‎ 又∵AD∥BC， ∴d＝a．‎ ‎∴由④式得 例10 已知：如图27－10(a)，以Rt△ABC的直角边AB为直径作⊙O，与斜边AC交于点D，过点D作⊙O的切线交BC边于点E．‎ 图27－10(a)‎ ‎(1)求证：EB＝EC＝ED；‎ ‎(2)试问在线段DC上是否存在点F，满足BC2＝4DF·DC?若存在，作出点F，并予以证明；若不存在，请说明理由．‎ 分析 (1)可知ED，EB均与⊙O相切，故ED＝EB．连接BD，可以构造Rt△BDC；或者连接OD，得OD⊥DE，然后得到EB，EC，ED的关系；(2)首先，BC2＝4DF·DCDE2＝DF·DC△DEF∽△DCE(很典型的图形)∠DEF＝∠C；其次，要使点F在线段CD上，则需∠DEF≤∠DEC．即需要∠C≤∠DEC∠C≤180°－2∠C0°＜∠C≤60°．‎ 解 (1)略；‎ ‎(2)在△DEC中，由于ED＝EC，‎ ‎∴∠C＝∠CDE．‎ ‎∴∠DEC＝180°－2∠C．‎ ‎①当∠DEC＞∠C时，有180°－2∠C＞∠C，即0°＜∠C＜60°时(如图27－10(a))，在线段DC上存在点F满足条件，即在∠DEC内，以ED为一边，作∠DEF，使∠DEF＝‎ ‎∠C，且EF交DC于点F，则点F即为所求．‎ ‎②当∠DEC＝∠C时(如图27－10(b))，△DEC为等边三角形，即∠DEC＝∠C＝60°．此时，C点即为满足条件的F点，于是DF＝DC＝DE，仍有BC2＝4DE2＝4DF·DC．‎ 图27－10(b)‎ ‎③当∠DEC＜∠C时(如图27－10(c))，有180°－2∠C＜∠C，即60°＜∠C＜90°，所作的∠DEF＞∠DEC，此时点F在DC的延长线上，故线段DC上不存在满足条件的点F．‎ 图27－10(c)‎ 说明 对于第(2)问的上述解答中，将BC用2DE替换后，可与等式右边的系数4约去，从而得到常规的等积式，想到构造相似三角形；亦可在连接BD后，由△BCD∽△ACB得出BC2＝CD·CA，从而BC2＝4DF·DC可变形为CD·CA＝4DF·DC，即CA＝4DF，即要探究在线段DC上是否存在点F，满足CA＝4DF．同学们可以自己解决．‎ 例11 已知：如图27－11(a)，在Rt△ACB中，∠C＝90°，AC＝4cm，BC＝3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t(s)(0＜t＜2)，解答下列问题：‎ 图27－11(a)‎ ‎(1)当t为何值时，PQ∥BC?‎ ‎(2)设△AQP的面积为y(cm2)，求y与t之间的函数关系式；‎ ‎(3)是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在，求出此时t的值．若不存在，说明理由；‎ ‎(4)如图27－11(b)，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形?若存在，求出此时菱形的边长；若不存在，说明理由．‎ 图27－11(b)‎ 解 (1)在Rt△ABC中，AB＝5．‎ 由题意知AP＝5－t，AQ＝2t．‎ 若PQ∥BC，则△APQ∽△ABC．‎ 解得 ‎(2)过点P作PH⊥AC于H，如图27－11(c)．‎ 图27－11(c)‎ ‎∵△APH∽△ABC，∴‎ 解得 ‎(3)若PQ把△ABC周长平分，‎ 则AP＋AQ＝BP＋BC＋CQ．‎ ‎∴(5－t)＋2t＝t＋3＋(4－2t)．‎ 解得t＝1．‎ 若PQ把△ABC面积平分，‎ 则，即 ‎∵t＝1代入上述方程不成立，‎ ‎∴不存在这一时刻t，使线段PQ把Rt△ACB的周长和面积同时平分．‎ ‎(4)过点P作PM⊥AC于M，PN⊥BC于N，如图27－11(d)．‎ 图27－11(d)‎ 若四边形PQP′C是菱形，那么PQ＝PC．‎ ‎∵PM⊥AC于M，∴QM＝CM．‎ ‎∵PN⊥BC于N，易知△PBN∽△ABC．‎ ‎．解得 ‎ 解得 ‎∴当时，四边形PQP′C是菱形．‎ 此时 在Rt△PMC中，‎ ‎∴菱形PQP′C的边长为．‎ 说明 探索点在运动中，对应形成几何图形的问题，实质上是一类利用数形结合思想寻求关于运动时间t的方程的解的问题．‎ 三、课标下新题展示 例12 点A，B分别是两条平行线m，n上任意两点，在直线n上找一点C，使BC＝k·AB．连接AC，在直线AC上任取一点E，作∠BEF＝∠ABC，EF交直线m于点F．‎ ‎(1)如图27－12(a)，当k＝1时，探究线段EF与EB的关系，并加以说明；‎ 说明 ①如果你经过反复探索没有解决问题，请写出探索过程(要求至少写三步)；‎ ‎②在完成①之后，可以自己添加条件(添加的条件限定为∠ABC为特殊角)，在图27－12(b)中补全图形，完成证明．‎ ‎(2)如图27－12(c)，若∠ABC＝90°，k≠1，探究线段EF与EB的关系，并说明理由．‎ ‎(a) (b) (c)‎ 图27－12‎ 解 (1)EF＝EB．‎ 证明：如图27－12(d)，以E为圆心，EA为半径画弧交直线m于点M，连接EM．‎ 图27－12(d)‎ ‎∴EM＝EA，∴∠EMA＝∠EAM．‎ ‎∵BC＝k·AB，k＝1，‎ ‎∴BC＝AB．‎ ‎∴∠CAB＝∠ACB．‎ ‎∵m∥n，∴∠MAC＝∠ACB，∠FAB＝∠ABC．‎ ‎∴∠MAC＝∠CAB．‎ ‎∴∠CAB＝∠EMA．‎ ‎∵∠BEF＝∠ABC，∴∠BEF＝∠FAB．‎ ‎∵∠AHF＝∠EHB，∴∠AFE＝∠ABE．‎ ‎∴△AEB≌△MEF．‎ ‎∴EF＝EB．‎ 探索思路：如图27－12(a)，∵BC＝k·AB，k＝1，∴BC＝AB．‎ ‎∴∠CAB＝∠ACB．‎ ‎∵m∥n，∴∠MAC＝∠ACB．‎ 添加条件：∠ABC＝90°．‎ 证明：如图27－12(e)，在直线m上截取AM＝AB，连接ME．‎ 图27－6(e)‎ ‎∵BC＝k·AB，k＝1，∴BC＝AB．‎ ‎∵∠ABC＝90°，∴∠CAB＝∠ACB＝45°．‎ ‎∵m∥n，∴∠MAE＝∠ACB＝∠CAB＝45°，∠FAB＝90°．‎ ‎∵AE＝AE，∴△MAE≌△BAE．‎ ‎∴EM＝EB，∠AME＝∠ABE．‎ ‎∵∠BEF＝∠ABC＝90°，‎ ‎∴∠FAB＋∠BEF＝180°．‎ ‎∴∠ABE＋∠EFA＝180°，又∵∠AME＋∠EMF＝180°，∴∠EMF＝∠EFA．‎ ‎∴EM＝EF．∴EF＝EB．‎ ‎(2)‎ 说明：如图27－12(f)，过点E作EM⊥m，EN⊥AB，垂足为M，N．‎ 图27－12(f)‎ ‎∴∠EMF＝∠ENA＝∠ENB＝90°．‎ ‎∵m∥n，∠ABC＝90°，‎ ‎∴∠MAB＝90°．‎ ‎∴四边形MENA为矩形．‎ ‎∴ME＝NA，∠MEN＝90°．‎ ‎∵∠BEF＝∠ABC＝90°．∴∠MEF＝∠NEB．‎ ‎∴△MEF∽△NEB．‎ 在Rt△ANE和Rt△ABC中，‎ 四、课标考试达标题 ‎(一)填空题 ‎1．观察下列各式：‎ ‎(x－1)(x＋1)＝x2－1，(x－1)(x2＋x＋1)＝x3－1，(x－1)(x3＋x2＋x＋1)＝x4－1，…，根据前面的规律，得(x－1)(xn＋xn－1＋…＋x＋1)＝______(n为正整数)．‎ ‎2．按下列图形的排列规律(其中是△三角形，□是正方形，○是圆)，□○△□□○△□○△□□○△□…，若第一个图形是正方形，则第2010个图形是______(填图形名称)．‎ ‎3．写出满足下列条件的一个一次函数：______，‎ ‎①y随x的增大而减小；②它的图象经过点(1，－2)．‎ ‎4．(1)如图27－13(a)，∠ABC＝∠DCB，请补充一个条件：______，使△ABC≌△DCB．(2)如图27－13(b)，∠1＝∠2，请补充一个条件：______，使△ABC∽△ADE．‎ 图27－13‎ ‎5．如图27－14，已知△ABC的面积S△ABC＝1，在图(a)中，若，则 在图(b)中，若则 在图(c)中，若则 ‎…‎ 按此规律，则若则则______．‎ 图27－14‎ ‎(二)解答题 ‎6．如图27－15，已知在梯形ABCD中，AD∥BC，AB＝DC，对角线AC和BD相交于点O，E是BC边上一个动点(点E不与B，C两点重合)，EF∥BD)交AC于点F，EG∥AC交BD于点G．‎ 图27－15‎ ‎(1)求证：四边形EFOG的周长等于2OB；‎ ‎(2)请你将上述题目的条件“梯形ABCD中，AD∥BC，AB＝DC”改为另一种四边形，其他条件不变，使得结论“四边形EFOG的周长等于2OB”仍成立，并将改编后的题目画出图形，写出已知、求证，不必证明．‎ ‎7．图27－16，平面直角坐标系内有两条直线l1，l2，直线l1的解析式为．如果将坐标纸折叠，使直线l1与l2重合，此时点(－2，0)与点(0，2)也重合．‎ 图27－16‎ ‎(1)求直线l2的解析式；‎ ‎(2)设直线l1与l2相交于点M．问：是否存在这样的直线l：y＝x＋t，使得如果将坐标纸沿直线l折叠，点M恰好落在x轴上?若存在，求出直线l的解析式；若不存在，请说明理由．‎ ‎8．如图27－17，∠ABM为直角，C为线段BA的中点，D是射线BM上的一个动点(不与点B重合)，连接AD，作BE⊥AD，垂足为E，连接CE，过点E作EF⊥CE，交BD于 F．‎ 图27－17‎ ‎(1)求证：BF＝FD；‎ ‎(2)∠A在什么范围内变化时，四边形ACFE是梯形?并说明理由；‎ ‎(3)∠A在什么范围内变化时，线段DE上存在点G，满足条件?并说明理由．‎ ‎9．如图27－18(a)、(b)、(c)，在△ABC中，分别以AB，AC为边，向△ABC外作正三角形、正四边形、正五边形，BE，CD相交于点O．‎ 图27－18‎ ‎(1)①如图27－18(a)，求证：△ADC≌△ABE；‎ ‎②探究：图27－18(a)中，∠BOC＝______；‎ 图27－18(b)中，∠BOC＝______；‎ 图27－18(c)中，∠BOC＝______；‎ ‎(2)如图27－18(d)，已知：AB，AD是以AB为边向△ABC外所作正n边形的一组邻边；AC，AE是以AC为边向△ABC外所作正n边形的一组邻边．BE，CD的延长相交于点O．‎ 图27－18(d)‎ ‎①猜想：图27－18(d)中，∠BOC＝______；‎ ‎(用含n的式子表示)‎ ‎②根据图27－18(d)证明你的猜想．‎ ‎2010中考数学考前冲刺最后一讲------开放型问题解题指导 参考答案 ‎ ‎ ‎1．xn＋1－1． 2．正方形．‎ ‎3．答案不唯一，满足k＜0且k＋b＝－2均可．‎ ‎4．答案不唯一．(1)如图(a)中∠A＝∠D，或AB＝DC；(2)图(b)中∠D＝∠B，或等．‎ ‎5．‎ ‎6．(1)证明：∵四边形ABCD是梯形，AD∥BC，AB＝CD，‎ ‎∴∠ABC＝∠DCB．‎ 又∵BC＝CB，AB＝DC，∴△ABC≌△DCB．‎ ‎∴∠1＝∠2．‎ 又∵GE∥AC，∴∠2＝∠3．∴∠1＝∠3．‎ ‎∴EG＝BG．‎ ‎∵EG∥OC，EF∥OB，‎ ‎∴四边形EGOF是平行四边形．‎ ‎∴EG＝OF，EF＝OG．‎ ‎∴四边形EGOF的周长＝2(OG＋GE)‎ ‎＝2(OG＋GB)＝2OB．‎ ‎(2)方法1：如答图27－1乙，已知矩形ABCD中，对角线AC，BD相交于点O，E为BC上一个动点(点E不与B，C两点重合)，EF∥BD，交AC于点F，EG∥AC交BD于点G．‎ 求证：四边形EFOG的周长等于2OB．图略．‎ 方法2：如图丙，已知正方形ABCD中，……其余略．‎ 答图27－1‎ ‎7．解：(1)直线l1与y轴交点的坐标为(0，1)．由题意，直线l1与l2关于直线y＝－x对称，直线l2与x轴交点的坐标为(－1，0)．‎ 又∵直线l1与直线y＝－x的交点为(－3，3)，‎ ‎∴直线l2过点(－1，0)和(－3，3)．‎ 设直线l2的解析式为y＝kx＋b．则有 解得 所求直线l2的解析式为 ‎(2)∵直线l与直线y＝－x互相垂直，且点M(－3，3)在直线y＝－x上，‎ ‎∴如果将坐标纸沿直线l折叠，要使点M落在x轴上，那么点M必须与坐标原点O重合，此时直线l过线段OM的中点 将代入y＝x＋t，解得t＝3．‎ ‎∴直线l的解析式为y＝x＋3．‎ ‎8．解：(1)Rt△AEB中，∵AC＝BC，‎ ‎∴CB＝CE．∴∠CEB＝∠CBE．‎ 答图27－2‎ ‎∵∠CEF＝∠CBF＝90°，‎ ‎∴∠BEF＝∠EBF．∴EF＝BF．‎ ‎∵∠BEF＋∠FED＝90°，‎ ‎∠EBD＋∠EDB＝90°，‎ ‎∴∠FED＝∠EDF．∴EF＝FD．‎ ‎∴BF＝FD．‎ ‎(2)由(1)得BF＝FD，而BC＝CA，‎ ‎∴CF∥AD，即AE∥CF．‎ 若AC∥EF，则 AC＝EF，∴BC＝BF．‎ ‎∴BA＝BD，∠A＝45°．‎ ‎∴当0°＜∠A＜45°或45°＜∠A＜90°时，四边形ACFE为梯形．‎ ‎(3)作GH⊥BD，垂足为H，则GH∥AB．‎ ‎∵‎ 又F为BD的中点，∴H为DF的中点．‎ ‎∴GH为DF的中垂线．‎ ‎∴∠GDF＝∠GFD．‎ ‎∵点G在ED上，∴∠EFD≥∠GFD．‎ ‎∵∠EFD＋∠FDE＋∠DEF＝180°，‎ ‎∴∠GFD＋∠FDE＋∠DEF≤180°．‎ ‎∴3∠EDF≤180°．‎ ‎∴∠EDF≤60°．‎ 又∠A＋∠EDF＝90°，‎ ‎∴30°≤∠A＜90°．‎ ‎∴当30°≤∠A＜90°时，DE上存在点G，满足条件 ‎9．解：(1)证法一：‎ ‎∵△ABD与△ACE均为等边三角形，‎ ‎∴AD＝AB，AC＝AE，且∠BAD＝∠CAE＝60°．‎ 答图27－3‎ ‎∴∠BAD＋∠BAC＝∠CAE＋∠BAC，‎ 即∠DAC＝∠BA E．‎ ‎∴△ADC△ABE．‎ 证法二：∵△ABD与△ACE均为等边三角形，‎ ‎∴AD＝AB，AC＝AE，‎ 且∠BAD＝∠CAE＝60°．‎ ‎∴△ADC可由△ABE绕着点A按顺时针方向旋转60°得到．‎ ‎∴△ABE≌△ADC．‎ ‎②120°，90°，72°．‎ ‎(2)①‎ ‎②证法一：依题意，知∠BAD和∠CAE都是正n边形的内角，AB＝AD，AE＝AC，‎ ‎∴∠BAD－∠DAE＝∠CAE－∠DAE，‎ 即∠BAE＝∠DAC．‎ ‎∴△ABE≌△ADC．‎ ‎∴∠ABE＝∠ADC．∵∠ADC＋∠ODA＝180°，‎ ‎∴∠ABO＋∠ODA＝180°．‎ ‎∴∠ABO＋∠ODA＋∠DAB＋∠BOC＝360°．‎ ‎∴∠BOC＋∠DAB＝180°．‎ ‎∴∠BOC＝180°－∠DAB＝‎ 证法二：延长BA交CO于F，‎ 证∠BOC＝∠DAF＝180°－∠BAD．‎ 证法三：连接CE．证∠BOC＝180°－∠CAE ‎ ‎