中考数学规律探索型几何类问题解决浅见 13页

⑴ 1+8=? 1+8+16=? ⑵ ⑶ 1+8+16+24=? …… 中考数学规律探索型（几何类）问题解决浅见 长旺中学 明道银 中考数学规律探索型问题的解决体现了新课程下数学中考 命题的新尝试，是近几年来中考的热点、重点和难点，需要敏锐 的观察力、严密的逻辑推理能力和一定的计算能力。为培养这方 面的能力，本人以几何图形的问题为例，从哪些方面来观察思考， 观察发现规律，并利用规律从特殊到一般和从一般到特殊的办法 来解决几何类规律探索型问题。 一、 规律明显 数数看看定有发现 例 1、如图，每一幅图中有若干个大小不同的菱形，第 1 幅 图中有 1 个，第 2 幅图中有 3 个，第 3 幅图中有 5 个，则第 n 幅 图中共有 个。 解析：方法 ：一数。在数字中发现。在开始的几幅图中把所 要的问题分别数字记载，如 1、3、5、7 、… ，发现奇数规律 排列，猜想最终结果为 2n-1 ；二看。发现图形规律和结果数字 规律。直接由图序排列发现大小菱形逐次各自多 1，得出所要的 结果是：1、1+2、1+2+2、1+2+2+2、… ，再发现是 1 加上若干 个 2 组成，2 的多少与序列号少 1，于是得 1+2（n-1）即 2n-1 。 例 2、观察下列图形及图形所对应的算式，根据你发现的规律 计算 1+8+16+24+……+8n（n 是正整数）的结果为 （ ）。 … … 第 1 幅 第 2 幅 第 3 幅 第 n 幅 解析：是图形规律与数字规律结合的问题，与上述比较多了 个数字条件规律，探究数字规律结果。 方法：在开始的几幅图中发现图形及图形所对应的算式之间 的关系，即：图形中小正方形的个数是图形所对应的算式的数值 结果；然后可直接由图形的规律发现结果或在数字形式（原式或 变形式或运算结果）发现结果。如在图形的规律发现结果为 3、5、 7、…、的平方；在原式数字形式发现结果为 1 加上若干个含 8 的 倍数的项的和，于是变形为 1+8（1+2+3+ … + n ）;在运算结果数 字规律 9、25、47、81 …中发现为 3、5、7、… 、的平方。 归纳方法：这类给定的图形或数字规律及寻找的数字规律容 易发现，通过一看二数三变的方法即可解决问题。 练习 1、用正三角形、正四边形和正六四边形按如图所示的 规律拼图案，即从第二个图案开始，每个图案中正三角形的个数 都比上一个图案中正三角形的个数多 4 个．则第 n 个图案中正三 角形的个数为 。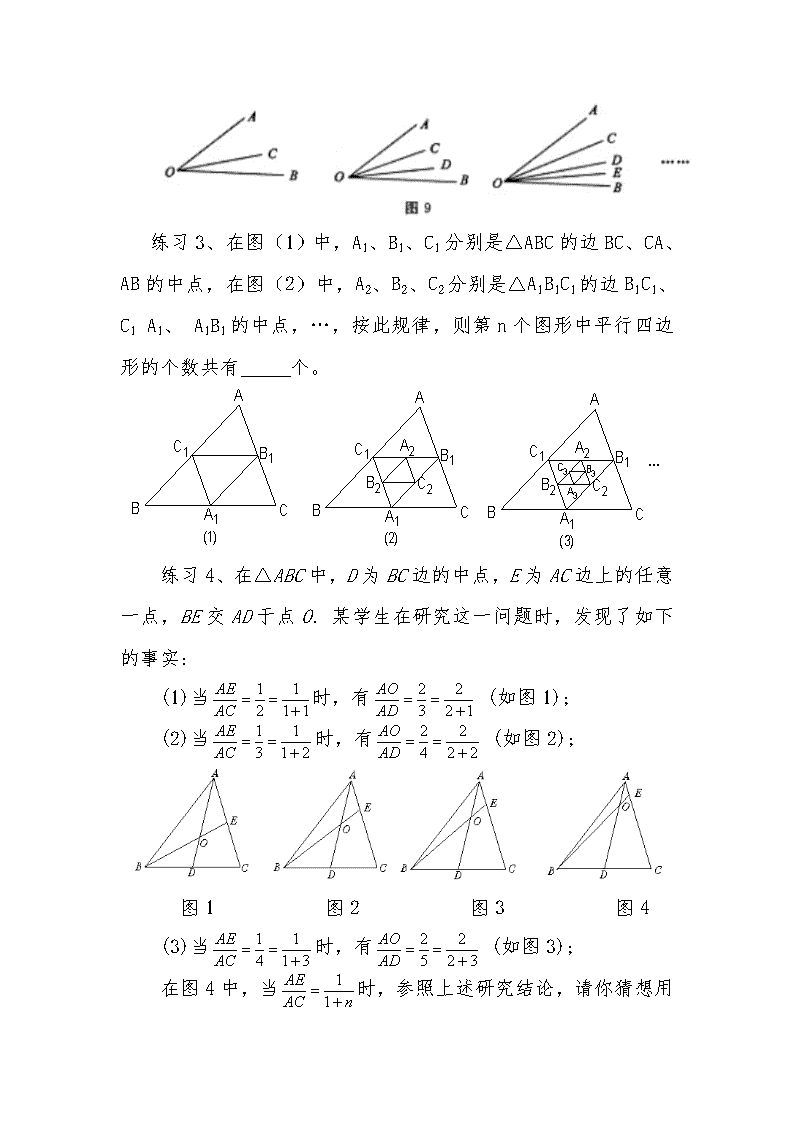 … 第一个图案 第二个图案 第三个图案 练习 2、、如图 9，在锐角 AOB 内部，画 1 条射线，可得 3 个锐角；画 2 条不同射线，可得 6 个锐角；画 3 条不同射线，可 得 10 个锐角；……照此规律，画 n 条不同射线，可得锐角 个． (3) (2) (1) C 3 B 3 A 3 A 2 C 1 B 1 A 1 C B A C 2 B 2 B 2 C 2 A B C A 1 B 1 C 1 A 2 C 1 B 1 A 1 C B A … 练习 3、在图（1）中，A1、B1、C1 分别是△ABC 的边 BC、CA、 AB 的中点，在图（2）中，A2、B2、C2 分别是△A1B1C1 的边 B1C1、 C1 A1、 A1B1 的中点，…，按此规律，则第 n 个图形中平行四边形 的个数共有 个。 练习 4、在△ABC 中，D 为 BC 边的中点，E 为 AC 边上的任意 一点，BE 交 AD 于点 O．某学生在研究这一问题时，发现了如下 的事实： (1)当 11 1 2 1  AC AE 时，有 12 2 3 2  AD AO (如图 1)； (2)当 21 1 3 1  AC AE 时，有 22 2 4 2  AD AO (如图 2)； 图 1 图 2 图 3 图 4 (3)当 31 1 4 1  AC AE 时，有 32 2 5 2  AD AO (如图 3)； 在图 4 中，当 nAC AE  1 1 时，参照上述研究结论，请你猜想用 B A C D A1 A2 A B C A1 A2 A3 B1 B2 B3 n 表示 AD AO 的一般结论，并给出证明(其中 n 是正整数)。 说明：证明时按照几何的探究思路和方法。 练习 5、如图，△ABC 的面积为 1，分别取 AC、BC 两边的中点 A1、B1，则四边形 A1ABB1 的面积为3 4 ，再分别取 A1C、B1C 的中点 A2、 B2，A2C、B2C 的中点 A3、B3，依次取下去…．利用这一图形，能直 观地计算出3 4 ＋3 42 ＋3 43 ＋…＋3 4n ＝________． 二、 规律隐含 算算数量待发现 例 3、如图，在△ABC 中，∠A＝ ．∠ABC 与∠ACD 的平分 线交于点 A1，得∠A1；∠A1BC 与∠A1CD 的平分线相交于点 A2， 得∠A2； ……；∠A2009BC 与∠A2009CD 的平分线相交于点 A2010， 得∠A2010，则∠A2010＝ ． 解析：（一） ∵∠A1 = ∠A1CD - ∠A1BD ，∠A1BC = 1 2 ∠ABC ∠A1CD = 1 2 ∠ACD = 1 2 （∠A +∠ABC ） ∴∠A1 = 1 2 ∠A 又∵∠A2 = ∠A2CD - ∠A2BD ，∠A2CD = 1 4 ∠ACD = 1 4 （∠A +∠ABC ） ，∠A2BC = 1 4 ∠ABC ∴∠A2 = 1 4 ∠A 同理，得∠A3 = 1 8 ∠A ；∠A4 = 1 16 ∠A ；∠A5 = 1 32 ∠A ∴∠An = 1 2 ∠A ∴∠A2010 = 1 2 ∠A 归纳方法：利用三角形的内角和或外角和的性质及角平分 线性质，采取从特殊到一般解决问题的数学思想，逐次探究出∠ A1 ；∠A2 ；∠A3 ；… ；∠An 的结果，发现一定的数量规律，猜 测结论。 解析：（二） ∵∠An = ∠AnCD - ∠AnBD ，∠AnBD = 1 2 ∠ABC ∠AnCD = 1 2 ∠ACD = 1 2 （∠A +∠ABC ） ∴∠An = 1 2 ∠A ∴∠A2010 = 1 2 ∠A 归纳方法：利用三角形的内角和或外角和的性质及角平分 线性质，采取从一般到特殊解决问题的数学思想，先探究出一般 情况下的的结果： ∠AnBD = 1 2 ∠ABC n 2010 n 2010 n nn n ∠AnCD = 1 2 ∠ACD = 1 2 （∠A +∠ABC ） 再利用外角和的性质探究出一般情况下的的结果： ∠An = ∠AnCD - ∠AnBD 最后进行代入计算，即得规律性的结果。 练习 1．如图，n+1 个上底、两腰长皆为 1，下底长为 2 的等 腰梯形的下底均在同一直线上，设四边形 P1M1N1N2 面积为 S1，四 边形 P2M2N2N3 的面积为 S2，……，四边形 PnMnNnNn+1 的面积记为 Sn， 通过逐一计算 S1，S2，…，可得 Sn = . A N1 N2 N3 N4 N5 P4P1 P2 P3 M1 M2 M3 M4 … 练习 2、如图，已知 Rt△ABC 中，AC=3，BC= 4，过直角顶点 C 作 CA1⊥AB，垂足为 A1，再过 A1 作 A1C1⊥BC，垂足为 C1，过 C1 作 C1A2⊥AB，垂足为 A2，再过 A2 作 A2C2⊥BC，垂足为 C2，…，这 样一直做下去，得到了一组线段 CA1，A1C1，C1A2，A2C2，…，AnCn， 则 AnCn＝ 。 A B C A1 A2 A3 A4 A5 C1C2C3C4C5 nn 练习 3、如图，如果以正方形 ABCD 的对角线 AC 为边作第二 个正方形 ACEF，再以对角线 AE 为边作第三个正方形 AEGH，如 此下去，…，已知正方形 ABCD 的面积 1s 为 1，按上述方法所作的 正方形的面积依次为 2s ， 3s … ns （n 为正整数），那么第 8 个正方 形的面积 ＝ . 练习 4、如图， 30AOB  ∠ ，过OA上到点O 的距离为 1，3，5，7，… 的点作OA 的垂线，分别与OB 相交，得到图所示的阴影梯形，它 们的面积依次记为 1 2 3S S S， ， ，…．则 2009S  三、 坐标规律 数形贯穿 庞杂难发现 例 4、如图， P1 是反比例函数 )0( ＞kx ky  在第一象限 图像上的一点，点 A1 的坐标为(2，0)，若△P1O A1 、△ P2 A1 A2 、…、 △Pn An-1 An 均为等边三角形，则 An 点 的坐标 是 ． O A B 1 3 5 7 9 11 13 15 … S1 S2 S3 S4 ns 解答思路：1、在等边三角形△P1O A1 中，易得点 P1（1 ，√3） 从而求的其反比例函数 xy 3 2、在等边三角形△Pn An-1 An 中，记 An 的坐标为（an ,0）过 点 Pn 做 PnH⊥x 轴于点 H， 则 PnH = 1 2 √3An-1 An = 1 2 √3（an - an-1 ） OH = OAn-1 + 1 2 An-1 An = an-1+ 1 2 （an - an-1 ）= 1 2 （an +an-1 ） 3、写出点 Pn 的坐标为〔 1 2（an +an-1 ） ， 1 2 √3（an - an-1 ）〕 代入其反比例函数 xy 3 得 an - an-1 = 4 4、作赋值计算 ∵a0 = 0 ；a1 = 2 2 2 2 22 2 ∴a1 = 4 ；a2 = 8 ；a3 = 12 ；a4 = 16 ； A5 = 20 ；a6 = 24；… ∴a1 = 2= 2√1 ；a2 = 2√2 ；a3 = 2√3 ； a4 = 2 √4；A5 = 2√5 ；a6 = 2√6；…… ； ∴an = 2√n ∴An 点的坐标是(2√n , 0 ) 归纳方法：这个问题如果采取从特殊到一般办法来解决，至少 要求得 A2、A3、A4、这三个点的坐标，方可发现一些规律，这样虽然 思维量小些，但运算量大；于是采取从一般到特殊的办法来解决，虽 然思维量大一些，但运算量小，能准确得出最终规律。但是要根据问 题的情形而定。 练习 1、如图，在平面直角坐标系中，有若干个整数点，其 顺序按图中“”方向排列，如（1，0），（2，0），（2，1），（3， 2），（3，1），（3，0）根据这个规律探索可得，第100个点的坐 标为 。 2 2 练习 2、如图，在直角坐标系中，四边形 ABCD 是正方形，A （1，-1）、B（-1，-1）、C（-1，1）、D（1， 1）.曲线 AA 1 A 2 A3… 叫做“正方形的渐开线”，其中 AA 1 、A 1 A 2 、A 2 A 3 …的圆心依次是 点 B、C、D、A 循环，则点 A 2010 的坐标是 。 练习 3、如图 15，△P1OA1，△P2A1A2，△P3A2A3……△PnAn－1An 都是等腰直角三角形，点 P1、P2、P3……Pn 都在函数 xy 4 (x > 0) 的图象上，斜边 OA1、A1A2、A2A3……An－1An 都在 x 轴上。则点 An 的坐标是 。 练习 4、如图 7 所示，P1（x1，y1）、P2（x2，y2），……Pn（xn， yn）在函数 y= x 9（x＞0）的图象上，△OP1A1，△P2A1A2，△P3A2A3…… △PnAn－1An……都是等腰直角三角形，斜边 OA1，A1A2……An-1An，都 在 x 轴上，则 y1+y2+…yn= 。 练习 5、如图 11，若第一个正方形 OABC 的顶点 B，第二个正 方形 ADEF 的顶点 E，….第 n 个正 方形的顶点 P 都在函数 1y x  （ 0x  ）的图象上，则点 P 的坐标是（ ， ）. 练习 6、如图 15，点 A 1 、A 2 、A 3 、……、A 1n 、A n 为 x 轴的 正半轴上的点，O A 1 = A 1 A 2 = A 2 A 3 =……=A 1n A n =1，分别以 A 1 、 A 2 、A 3 、……、A 1n 、A n 为直角顶点作 Rt△OA 1 B 1 、Rt△A1A 2 B 2 、 Rt△A 2 A 3 B 3 、……、Rt△A 1n A n B n ，它们的面积分别记为 S 1 、 S 2 、S 3 、……、S n ，且 S 1 =1；双曲线恰好经过点 B 1 、B 2 、B 3 、……、 B n 。（1）求双曲线和直线 A 1 B 2 对应的函数解析式； （2）填空：S 10 =___________，S n =_____________； （3）若直线 B 1 O 交双曲线于另一点 P，有三位同学在研究直 线 A 1 B 2 、直线 A 2 B 3 、……、直线 A 1n B n 这系列直线时，有如下 发现： ①小明说：“我发现直线 A 1 B 2 经过 P 点” ②小亮说：“我发现直线 A 1 B 2 和直线 A 2 B 3 都经过 P 点” ③小王说：“我发现直线 A 1 B 2 和直线 A 2 B 3 、……、直线 A 1n B n 都经过 P 点” 请问：上述三位同学的发现，谁的发现更准确？并给予说明。 练习 7、正方形 A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的 方式放置．点 A1，A2，A3，…和点 C1，C2，C3，…分别在直线 y kx b  (k ＞0)和 x 轴上，已知点 B1(1，1)，B2(3，2)，则 Bn 的坐标是 ． 练习 8、如图所示，已知：点 (0 0)A ， ， ( 3 0)B ， ， (01)C ， 在 ABC△ 内依次作等边三角形，使一边在 x 轴上，另一个顶点在 BC 边上，作出的等边三角形分别是第 1 个 1 1AA B△ ，第 2 个 1 2 2B A B△ ，第 3 个 2 3 3B A B△ ，…，则第 n 个等边三角 形的边长等于 ． 练习 9、如图，在直角坐标系中，一直线 l 经过点 ( 3,1)M 与 x 轴，y 轴分别交于 A、B 两点，且 MA＝MB，则△ABO 的内切圆 1o 的半径 1r ＝ ；若 2o 与 1o 、l 、y 轴分别相切， 3o 与 2o 、l 、y 轴分别相切，…，按此规律，则 20080 的半径 2008r ＝ 练习 10、二次函数 22 3y x 的图象如图 12 所示，点 0A 位于坐标原点， 点 1A ， 2A ， 3A ，…， 2008A 在 y 轴的正半轴上，点 1B ， 2B ， 3B ，…， 2008B y xO C1 B2 A2 C3 B1 A3 B3 A1 C2 O y x(A) A1 C1 1 2B A2 A3 B3B2B1 0 x y A B M O O O 在二次函数 22 3y x 位于第一象限的图象上，若△ 0 1 1A B A ,△ 1 2 2A B A ，△ 2 3 3A B A ，…，△ 2007 2008 2008A B A 都为等边三角形，则△ 2007 2008 2008A B A 的边 长＝ . 练 习 11 、 对 于 每 个 非 零 自 然 数 n ， 抛 物 线     2 2 1 1 1 1 ny x xn n n n     与 x 轴交于 nA 、 nB 两点，以 n nA B 表示这两 点间的距离，则 1 1 2 2A B A B  … 2009 2009A B 的值是（ ） A． 2009 2008 B． 2008 2009 C． 2010 2009 D． 2009 2010