贵阳市中考数学试题及答案解析 15页

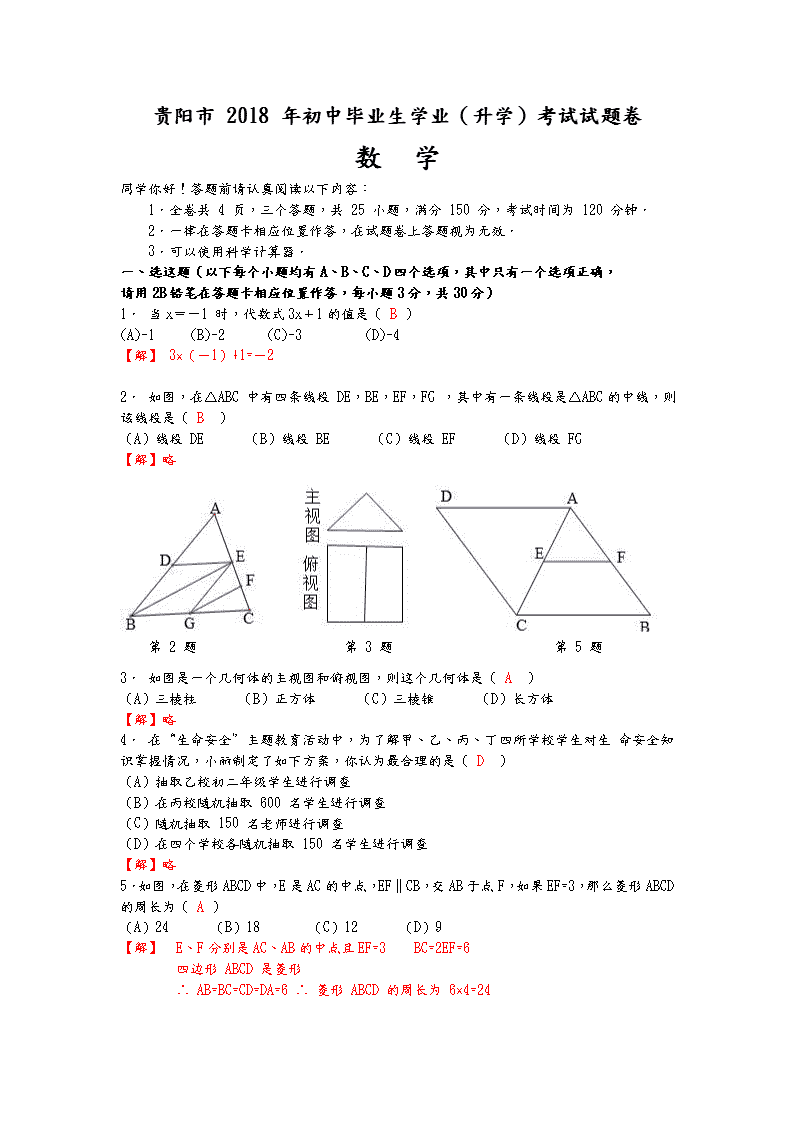
贵阳市 2018 年初中毕业生学业（升学）考试试题卷 数 学 同学你好！答题前请认真阅读以下内容：‎ ‎1．全卷共 4 页，三个答题，共 25 小题，满分 150 分，考试时间为 120 分钟．‎ ‎2．一律在答题卡相应位置作答，在试题卷上答题视为无效．‎ ‎3．可以使用科学计算器．‎ 一、选这题（以下每个小题均有A、B、C、D四个选项，其中只有一个选项正确，‎ 请用2B铅笔在答题卡相应位置作答，每小题3分，共30分）‎ ‎1． 当x＝－1 时，代数式3x＋1的值是（ B ）‎ ‎(A)-1 (B)-2 (C)-3 (D)-4‎ ‎【解】 3×（－1）+1=－2‎ ‎2． 如图，在△ABC 中有四条线段 DE，BE，EF，FG ，其中有一条线段是△ABC的中线，则该线段是（ B ）‎ ‎（A）线段 DE （B）线段 BE （C）线段 EF （D）线段 FG ‎【解】略 ‎ ‎ 第 2 题 第 3 题 第 5 题 ‎3． 如图是一个几何体的主视图和俯视图，则这个几何体是（ A ）‎ ‎（A）三棱柱 （B）正方体 （C）三棱锥 （D）长方体 ‎【解】略 ‎4． 在“生命安全”主题教育活动中，为了解甲、乙、丙、丁四所学校学生对生 命安全知识掌握情况，小丽制定了如下方案，你认为最合理的是（ D ）‎ ‎（A）抽取乙校初二年级学生进行调查 ‎ ‎（B）在丙校随机抽取 600 名学生进行调查 ‎（C）随机抽取 150 名老师进行调查 ‎（D）在四个学校各随机抽取 150 名学生进行调查 ‎【解】略 ‎5．如图，在菱形ABCD中，E是AC的中点，EF∥CB，交AB于点F，如果EF=3，那么菱形ABCD的周长为（ A ）‎ ‎（A）24 （B）18 （C）12 （D）9‎ ‎【解】QE、F分别是AC、AB的中点且EF=3 BC=2EF=6‎ 四边形 ABCD 是菱形 ‎∴ AB=BC=CD=DA=6 ∴ 菱形 ABCD 的周长为 6×4=24‎ ‎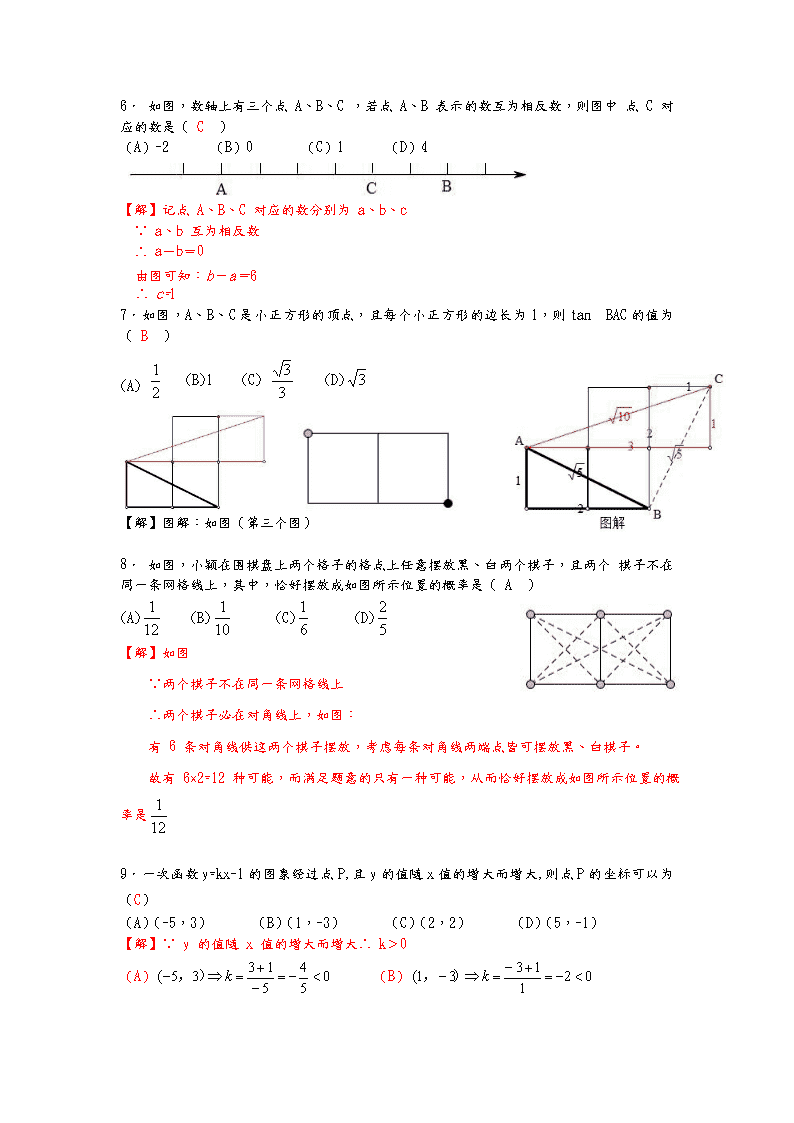6． 如图，数轴上有三个点 A、B、C ，若点 A、B 表示的数互为相反数，则图中 点 C 对应的数是（ C ）‎ ‎（A）-2 （B）0 （C）1 （D）4‎ ‎【解】记点 A、B、C 对应的数分别为 a、b、c Q∵ a、b 互为相反数 ∴ a－b＝0‎ 由图可知： b－ a＝6‎ ‎∴ c=1‎ ‎7．如图，A、B、C是小正方形的顶点，且每个小正方形的边长为1，则tanÐBAC的值为（ B ）‎ (A) ‎ (B)1 (C) (D)‎ ‎ ‎ ‎【解】图解：如图（第三个图）‎ ‎8． 如图，小颖在围棋盘上两个格子的格点上任意摆放黑、白两个棋子，且两个 棋子不在同一条网格线上，其中，恰好摆放成如图所示位置的概率是（ A ）‎ ‎(A) (B) (C) (D)‎ ‎【解】如图 ‎∵两个棋子不在同一条网格线上 ‎∴两个棋子必在对角线上，如图：‎ 有 6 条对角线供这两个棋子摆放，考虑每条对角线两端点皆可摆放黑、白棋子。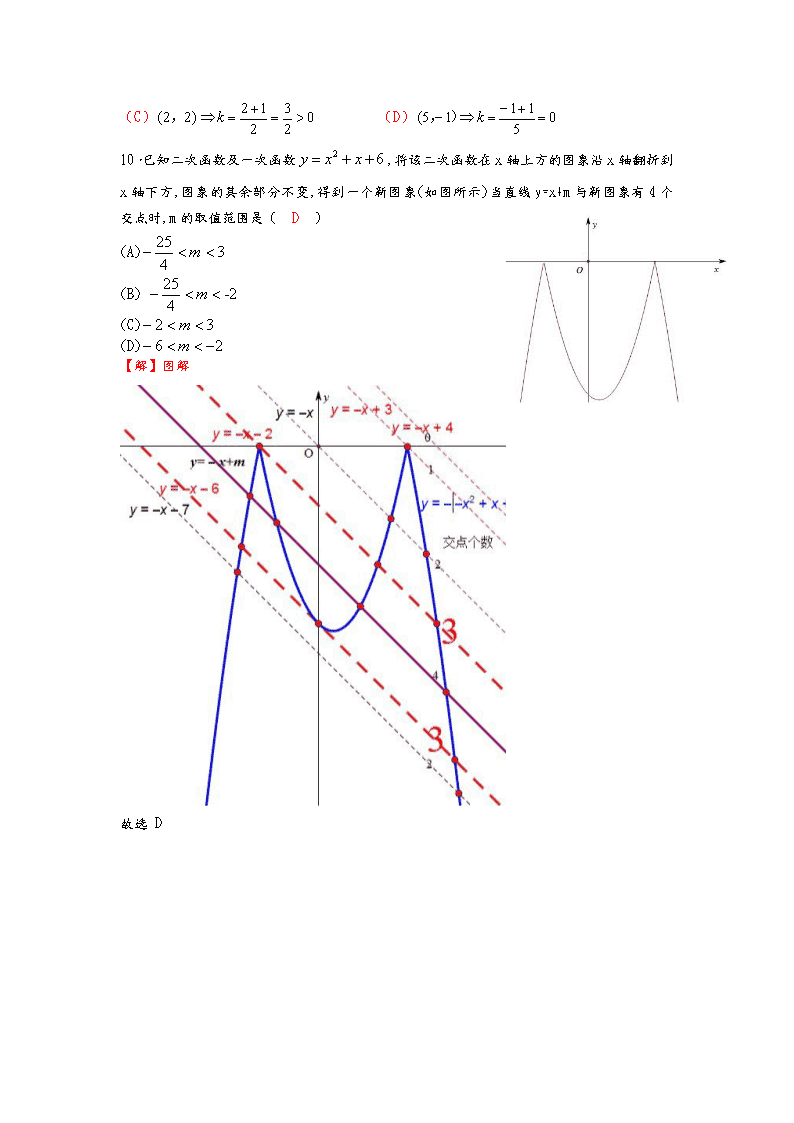‎ 故有 6×2=12 种可能，而满足题意的只有一种可能，从而恰好摆放成如图所示位置的概率是 ‎9．一次函数y=kx-1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为（C）‎ ‎（A）（-5，3） （B）（1，-3） （C）（2，2） （D）（5，-1）‎ ‎【解】∵ y 的值随 x 值的增大而增大∴ k＞0‎ （A） ‎ （B）‎ ‎（C） （D）‎ ‎10．已知二次函数及一次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示)当直线y=x+m与新图象有4个交点时,m的取值范围是（ D ）‎ ‎(A)‎ ‎(B) ‎ ‎(C)‎ ‎(D)‎ ‎【解】图解 故选 D 二、填空题（每小题 4 分，共 20 分）‎ ‎11．某班 50 名学生在 2018 年适应性考试中，数学成绩在 100～110 分这个分数段的频率为 0.2，则该班在这个分数段的学生为 10 人．‎ ‎【解】 频数=总数×频率＝50*0.2＝10‎ ‎12.如图,过x轴上任意一点P作y轴的平行线,分别与反比例函数(x>0)的图象交于A点和B点,若C为y轴上任意一点,连接AC,BC,则△ABC的面积为 9/2 .‎ ‎13.如图,点M,N分别是正五边形ABCDE的两边AB,BC上的点,且AM=BN,点O是正五边形的中心,则∠MON的度数是 72 度 ‎ ‎ ‎12题【解】如图 ‎ ‎ ‎13【解】略 ‎14．已知关于x的不等式组无解,则a的取值范围是 a≥2 ‎ ‎【解】‎ 解不等式5-3x≥-1得：x≤2‎ 解不等式a-x<0得：x>a ‎ ‎ ‎（1）当a<2时，有解a2时无解，a=2时有解。我们认为，当a=2时，不能满足a-x<0，所以值得讨论。‎ ‎15.如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB,AC边上,则对角线EG长的最小值为 ‎【解】∵四边形 DEFG 是矩形 ‎∴DG∥EF，ADG ∽ABC ‎∴ ，即 ‎∴‎ 在Rt△EDG中 三、解答题（本大题 10 个小题，共 100 分）‎ ‎17．（本题满分 10 分）在 6·26 国际禁毒日到来之际，贵阳市教育局为了普及禁 毒知识，提高禁毒意识，举办了“关爱生命，拒绝毒品”的知识竞赛．某校初一、‎ 初二年级分别有 300 人，现从中各随机抽取 20 名同学的测试成绩进行调查分析，‎ 成绩如下：‎ 初一 ‎68‎ ‎88‎ ‎100‎ ‎100‎ ‎79‎ ‎94‎ ‎89‎ ‎85‎ ‎100‎ ‎88‎ ‎100‎ ‎90‎ ‎98‎ ‎97‎ ‎77‎ ‎94‎ ‎96‎ ‎100‎ ‎92‎ ‎67‎ 初二 ‎69‎ ‎97‎ ‎96‎ ‎89‎ ‎98‎ ‎100‎ ‎99‎ ‎100‎ ‎95‎ ‎100‎ ‎99‎ ‎69‎ ‎97‎ ‎100‎ ‎99‎ ‎94‎ ‎79‎ ‎99‎ ‎98‎ ‎79‎ ‎(1)根据上述数据,将下列表格补充完整：‎ 整理、描述数据:‎ 分数段 ‎60≤x≤69‎ ‎70≤x≤79‎ ‎80≤x≤89‎ ‎90≤x≤100‎ 初一人数 ‎2‎ ‎2‎ ‎4‎ ‎12‎ 初二人数 ‎2‎ ‎2‎ ‎1‎ ‎15‎ 分析数据:样本数据的平均数、中位数、满分率如下表 年级 平均数 中位数 满分率 初一 ‎90.1‎ ‎93‎ ‎25%‎ 初二 ‎92.8‎ ‎▲‎ ‎20%‎ 得出结论:‎ ‎(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 ▲ 人；‎ ‎(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.‎ ‎【解】(1)97.5‎ ‎（2）估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共135人；‎ ‎（3）你认为哪个年级掌握禁毒知识的总体水平较好，说明理由.‎ 初二年级总体掌握禁毒知识水平较好，因为平均数和中位数都高于初一年级 ‎17.(本题满分8分)‎ 如图,将边长为m的正方形纸板沿虚线剪成两个小正方形和两个矩形.拿掉边长为n的小正方形纸板后,再将剩下的三块拼成一个新矩形.‎ ‎(1)用含m或n的代数式表示拼成的矩形周长；‎ ‎(2)当m=7,m=4时,求拼成的矩形面积.‎ ‎【解】(1)‎ 解法一：拼图如图：周长=2[（m+n)+(m-n)]=2(2m)=4m 解法二：原图计算，拼图前后周长不变，且拿掉边长为n的正方形后，n仅发生位置变化，边长为4m ‎【解】(2)‎ 解法一：原图：‎ 解法二：拼图：‎ ‎18.(本题满分8分)‎ 如图①,在Rt△ABC中,以下是小亮探索与之间关系的方法:‎ 根据你掌握的三角函数知识,在图②的锐角△ABC中,探索之间的关系,并写出探索过程.‎ ‎【解】作CM⊥AB于点M，作AN⊥BC于点N,如图所示：‎ 在 Rt△AMC中：‎ 在 Rt△BMC中：‎ 在 Rt△ANC 中：‎ 在 Rt△ANB中：‎ ‎19．（本题满分10分）某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．‎ ‎（1）求甲、乙两种树苗每棵的价格各是多少元？‎ ‎（2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵．此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？‎ ‎【解】（1）设甲种树苗每棵的价格是x元，则乙种树苗每棵的价格是x+10元。‎ 得方程：‎ 解得：，乙种树苗的价格为30+10=40元/棵。‎ 答：甲种树苗人格为30元/棵，乙种树苗价格为40元/棵。‎ ‎【解】（2）设可购买乙种树苗y棵，则可购买甲种树苗为（50-y）棵。‎ 根据（1）的结果可知，甲种树苗的现价格为30×（1-10%）=27元/棵 得不等式：‎ 解得：‎ 答：他们量多可以购买乙种树苗11棵 ‎20.(本题满分10分)如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称。‎ ‎(1)求证:△AEF是等边三角形；‎ ‎(2)若AB=2,求△AFD的面积.‎ 解2：由（1）知：△AEF为等边三角形 又AB与AG关于AE对称,AE与AF关于AG对称 ‎∴△BAG为等边三角形，∠B=60°‎ ‎∵AE⊥BC，AB=2，‎ 在Rt△EAD中，∠AED=60°,∠EDA=30°,‎ FD=FE=AE=‎ 过点F作△AFD的高FH，则FH=‎ AD=2HD=‎ 证明（1）‎ ‎∵四边形ABCD是平行四边形 ‎∴AD∥BC ‎∵AE⊥BC ‎∴AE⊥AD 即∠EAD＝90°‎ 在Rt△EAD中 ‎∵F是ED的中点 ‎∵AE与AF关于AG对称 ‎∴AE=AF ‎∴AE=AF=EF ‎∴AEF是等边三角形 ‎21．（本题满分10分）图①是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字1，2，3，4，图②是一个正六边形棋盘．现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子掷出后，看骰子向上三个面（除底面外）的数字之和是几，就从图②中的A点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处开始，按第一次的方法跳动．‎ ‎（1）随机掷一次骰子，则棋子跳动到点C处的概率是；‎ ‎（2）随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点C处的概率．‎ 图1 图2‎ ‎【解】随机掷一次骰子，骰子向上三个面（除底面外）的数字之和可以是 6、7、8、9.‎ ‎（1）随机掷一次骰子，满足棋子跳动到点 C 处的数字是 8‎ 所以，随机掷一次骰子，则棋子跳动到点 C 处的概率是 ‎（2）随机掷两次骰子，棋子最终跳动到点C处的数字是14，列表如下：‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎6‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎7‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎8‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎9‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ 树状图如下：‎ 所以，随机掷两次骰子，棋子最终跳动到点 C 处的概率是 ‎22.(本题满分10分)‎ 六盘水市梅花山国际滑雪场自建成以来,吸引了大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:m)与滑行时间x(单位:s)之间的关系可以近似地用二次函数来表示,现测得一组数据,如下表所示 滑行时间x/s ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ 滑行距离y/m ‎0‎ ‎4‎ ‎12‎ ‎24‎ ‎…‎ ‎(1)根据表中数据求出二次函数的表达式,现测量出滑雪者的出发点与终点的距离大约840米,他需要多少时间才能到达终点?‎ ‎(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向下平移5个单位,求平移后所得函数的表达式.‎ 解(1)：设函数的表达式为，将数组代入函数得：‎ ‎ 解得 得函数表达式： ‎ 当y=840时，。解得 因为x>0，所以x=20‎ 答：函数表达式为 ,他需要20s才能到达终点 解（2）：画图略 由（1）知 向左平移2各单位得：‎ 向上平移5个单位得：‎ ‎23.(本题满分10分)‎ 如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB，垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E.设△OPE的内心为M,连接OM,PM.‎ ‎(1)求∠OMP的度数 ‎(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.‎ ‎【解】（1）‎ ‎∵PE⊥OC ‎∴∠PEO＝90°‎ ‎∴∠EPO+∠EOP＝90° ‎∵M是△OPE的内心 ‎∴∠EOM=POM，∠EPM=∠OPM ‎∴∠POM+∠OPM=(∠EPO+∠EOP)=45°‎ 在△POM中，∠OMP=180°-(∠POM+∠OPM)=180°-45°=135°‎ ‎（2）连接CM，作过O、M、C三点的外接圆，即⊙N，连接NC、NO，在⊙N的优弧上任取一点H，连接HC、HO.如图所示：‎ 由题意知：OP=OC，∠POM=∠COM，OM=OM ‎∴△POM≌△COM ‎∴∠OMP=∠OMC=135‎ 在⊙N的内接四边形CMOH中，∠H=180°-∠OMC=180°-135°=45°‎ ‎∴∠N=2×45°=90°‎ 由题意知：‎ 在等腰直角三角形CNO中，NC=NO 由勾股定理得：,‎ 当点P在弧BC上运动时，点M在弧OC上运动 ‎∵弧BC与弧AC关于OC对称 ‎∴当点P在弧CA上运动时，点M所在弧上的运动路径长与当点P在弧BC 上运动时，点M在上运动的路径长相等 ‎∴当点P在半圆上从点B运动到点A时，求内心M所经过的路径长为：‎ ‎24.(本题满分12分)‎ 如图,在矩形ABCD中,AB=2,AD=,P是BC边上的一点,且BP=2CP.‎ ‎(1)用尺规在图①中作出CD边上的中点E,连接AE,BE(保留作图痕迹,不写作法)；‎ ‎(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由；‎ ‎(3)如图③,在(2)的条件下,连接EP并延长交AB的延长线于点F,连接AP.不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?‎ 如果能，说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向、旋转角或平移方向和平移距离)；如果不能,也请说明理由.‎ ‎(图①) (图②) (图③)‎ ‎【解】（1）作图略 ‎（2）EB平分∠AEC 理由如下：‎ ‎∵AB=DC=2，CE=DC/2=1，BC=AD=‎ ‎∴‎ ‎∴∠BEC=60°,BE=AE=2EC=2,△ABE是等边三角形 ‎∴∠AEB=60°‎ ‎∴EB平分∠AEC ‎（3）△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形 只需证明△PFB、△PAB、△PEA全等，再通过翻转、旋转即可 ‎25.(本题满分12分)‎ 如图,在平面直角坐标系xoy中,点A是反比例函数(x>0,m>1)图象上一点,点A的横坐标为m,点B(0，-m)是y轴负半轴上的一点，连接AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC.过点A作AE平行于x轴,过点D作y轴的平行线交AE于点E.‎ ‎(1)当m=3时,求点A的坐标；‎ ‎(2)DE= ▲ :设点D的坐标为(x,y),求y关于x的函数关系式和自变量的取值范围；‎ ‎(3)连接BD,过点A作BD的平行线,与(2)中的函数图象交于点F,当m为何值时,以A,B,D,F为顶点的四边形是平行四边形?‎ 解（1）：‎ ‎∵点A的横坐标为m ‎∴当m=3时，，‎ ‎∴点A（3，6）‎ ‎（2）作AF⊥y轴于点F，则∠CFA＝90°，由题意知：A(m,m2-m)，B(0，-m)‎ Q∵CA⊥AB ==> ∠CAB＝90°‎ 又∵∠CAB=∠CFA=90°‎ ‎∴∠ABC+∠FAB＝∠FAB+∠CAF＝90° ==> ∠ABC＝∠CAF ‎∴Rt△AFC∽Rt△BFA 得CF=1‎ ‎∵AD=AC，∠E=∠AFC=90°，∠CAF=∠DAE ‎∴Rt△AFC≌Rt△AED ‎∴AE=AF=m，DE=CF=1‎ ‎∴‎ ‎∴‎ 消去m得 ‎ x>2‎ 答：DE=1，，x>2‎ ‎（3）x＞2，A(m,m2-m)，B(0，-m)，D(2m，m2-m-1)‎ 方法一：利用平行四边形对角线互相平分以及中点坐标公式 当AB为对角线时 得：，代入 得：‎ 解得：（均小于2，舍去）‎ 考虑到二次函数图像不完整，只有x>2部分，故此情况不用写 当AD为对角线时：‎ 得：，代入 得：‎ 解得：‎ 当m=2时，以A、B、D、F为顶点的四边形是平行四边形 方法二：坐标平移法（对边相等+点平移方向相同）‎ 得：，代入 得：‎ 解得：‎ 或：‎ 得：，代入 得：‎ 解得：（均小于2，舍去）‎ 考虑到二次函数图像不完整，只有x>2部分，故此情况不用写 ‎∴当m=2时，以A、B、D、F为顶点的四边形是平行四边形