乐山市中考数学试卷含答案解析 40页

四川省乐山市2017年中考数学试卷 一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项符合题目要求．‎ ‎1．（3分）﹣2的倒数是（　　）‎ A．﹣ B． C．2 D．﹣2‎ ‎2．（3分）随着经济发展，人民的生活水平不断提高，旅游业快速增长，2016年国民出境旅游超过120 000 000人次，将120 000 000用科学记数法表示为（　　）‎ A．1.2×109 B．12×107 C．0.12×109 D．1.2×108‎ ‎3．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎4．（3分）含30°角的直角三角板与直线l1、l2的位置关系如图所示，已知l1∥l2，∠ACD=∠A，则∠1=（　　）‎ A．70° B．60° C．40° D．30°‎ ‎5．（3分）下列说法正确的是（　　）‎ A．打开电视，它正在播广告是必然事件 B．要考察一个班级中的学生对建立生物角的看法适合用抽样调查 C．在抽样调查过程中，样本容量越大，对总体的估计就越准确 D．甲、乙两人射中环数的方差分别为S甲2=2，S乙2=4，说明乙的射击成绩比甲稳定 ‎6．（3分）若a2﹣ab=0（b≠0），则=（　　）‎ A．0 B． C．0或 D．1或 2‎ ‎7．（3分）如图是“明清影视城”的一扇圆弧形门，小红到影视城游玩，他了解到这扇门的相关数据：这扇圆弧形门所在的圆与水平地面是相切的，AB=CD=0.25米，BD=1.5米，且AB、CD与水平地面都是垂直的．根据以上数据，请你帮小红计算出这扇圆弧形门的最高点离地面的距离是（　　）‎ A．2米 B．2.5米 C．2.4米 D．2.1米 ‎8．（3分）已知x+=3，则下列三个等式：①x2+=7，②x﹣，③2x2﹣6x=﹣2中，正确的个数有（　　）‎ A．0个 B．1个 C．2个 D．3个 ‎9．（3分）已知二次函数y=x2﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（　　）‎ A． B． C．或 D．或 ‎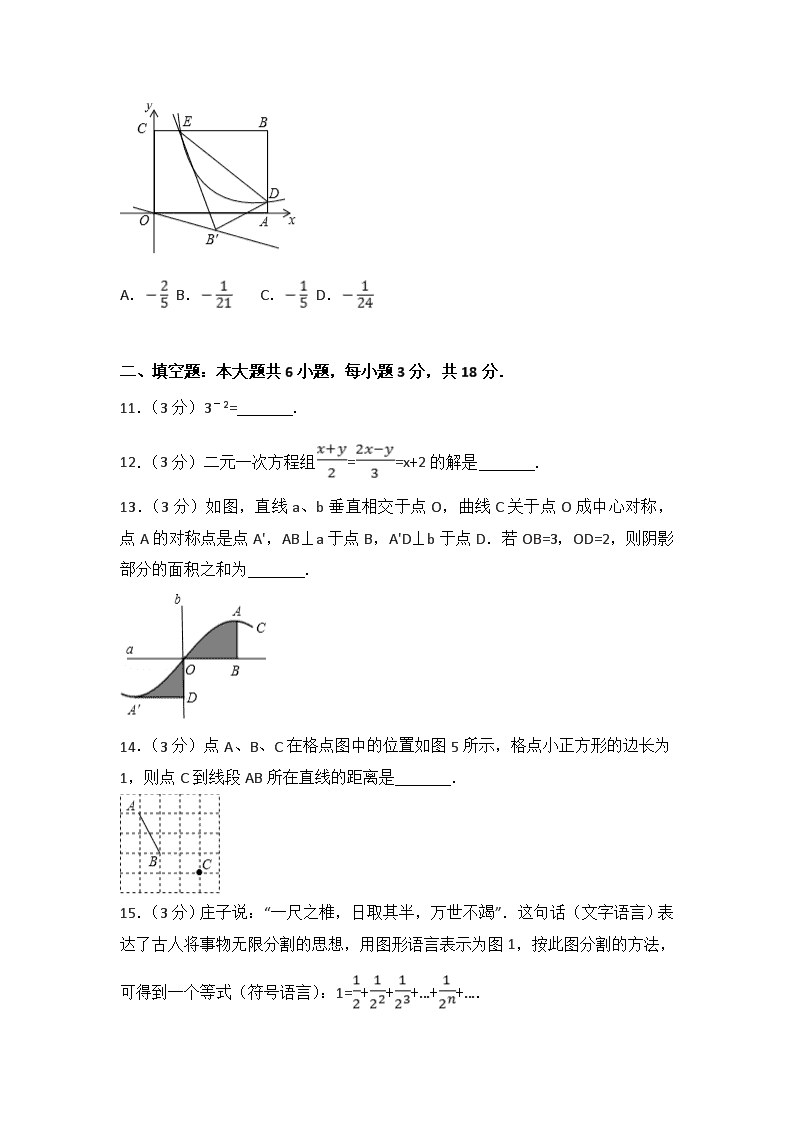10．（3分）如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数y=的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（　　）‎ A． B． C． D． ‎　‎ 二、填空题：本大题共6小题，每小题3分，共18分．‎ ‎11．（3分）3﹣2=　 　．‎ ‎12．（3分）二元一次方程组==x+2的解是　 　．‎ ‎13．（3分）如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D．若OB=3，OD=2，则阴影部分的面积之和为　 　．‎ ‎14．（3分）点A、B、C在格点图中的位置如图5所示，格点小正方形的边长为1，则点C到线段AB所在直线的距离是　 　．‎ ‎15．（3分）庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言）：1=+++…++…．‎ 图2也是一种无限分割：在△ABC中，∠C=90°，∠B=30°，过点C作CC1⊥AB于点C1，再过点C1作C1C2⊥BC于点C2，又过点C2作C2C3⊥AB于点C3，如此无限继续下去，则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、…．假设AC=2，这些三角形的面积和可以得到一个等式是　 　．‎ ‎16．（3分）对于函数y=xn+xm，我们定义y'=nxn﹣1+mxm﹣1（m、n为常数）．‎ 例如y=x4+x2，则y'=4x3+2x．‎ 已知：y=x3+（m﹣1）x2+m2x．‎ ‎（1）若方程y′=0有两个相等实数根，则m的值为　 　；‎ ‎（2）若方程y′=m﹣有两个正数根，则m的取值范围为　 　．‎ ‎　‎ 三、本大题共3小题，每小题9分，共27分.‎ ‎17．（9分）计算：2sni60°+|1﹣|+20170﹣．‎ ‎18．（9分）求不等式组的所有整数解．‎ ‎19．（9分）如图，延长▱ABCD的边AD到F，使DF=DC，延长CB到点E，使BE=BA，分别连结点A、E和C、F．求证：AE=CF．‎ ‎　‎ 四、本大题共3小题，每小题10分，共30分．‎ ‎20．（10分）化简：（﹣）÷．‎ ‎21．（10分）为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：‎ 组别 分数段（分）‎ 频数 频率 A组 ‎60≤x＜70‎ ‎30‎ ‎0.1‎ B组 ‎70≤x＜80‎ ‎90‎ n C组 ‎80≤x＜90‎ m ‎0.4‎ D组 ‎90≤x＜100‎ ‎60‎ ‎0.2‎ ‎（1）在表中：m=　 　，n=　 　；‎ ‎（2）补全频数分布直方图；‎ ‎（3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在　 　组；‎ ‎（4）4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明．‎ ‎22．（10分）如图，在水平地面上有一幢房屋BC与一棵树DE，在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°，∠CAD=60°，在屋顶C处测得∠DCA=90°．若房屋的高BC=6米，求树高DE的长度．‎ ‎　‎ 五、本大题共2小题，每小题10分，共20分.‎ ‎23．（10分）某公司从2014年开始投入技术改进资金，经技术改进后，其产品的成本不断降低，具体数据如下表：‎ 年 度 ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ 投入技改资金x（万元）‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ 产品成本y（万元/件）‎ ‎7.2‎ ‎6‎ ‎4.5‎ ‎4‎ ‎（1）请你认真分析表中数据，从一次函数和反比例函数中确定哪一个函数能表示其变化规律，给出理由，并求出其解析式；‎ ‎（2）按照这种变化规律，若2017年已投入资金5万元．‎ ‎①预计生产成本每件比2016年降低多少万元？‎ ‎②若打算在2017年把每件产品成本降低到3.2万元，则还需要投入技改资金多少万元？（结果精确到0.01万元）．‎ ‎24．（10分）如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连结PC交AB于点E，且∠ACP=60°，PA=PD．‎ ‎（1）试判断PD与⊙O的位置关系，并说明理由；‎ ‎（2）若点C是弧AB的中点，已知AB=4，求CE•CP的值．‎ ‎　‎ 六、本大题共2小题，第25题12分，第26题13分，共25分.‎ ‎25．（12分）在四边形ABCD中，∠B+∠D=180°，对角线AC平分∠BAD．‎ ‎（1）如图1，若∠DAB=120°，且∠B=90°，试探究边AD、AB与对角线AC的数量关系并说明理由．‎ ‎（2）如图2，若将（1）中的条件“∠B=90°”去掉，（1）中的结论是否成立？请说明理由．‎ ‎（3）如图3，若∠DAB=90°，探究边AD、AB与对角线AC的数量关系并说明理由．‎ ‎26．（13分）如图1，抛物线C1：y=x2+ax与C2：y=﹣x2+bx相交于点O、C，C1与C2分别交x轴于点B、A，且B为线段AO的中点．‎ ‎（1）求 的值；‎ ‎（2）若OC⊥AC，求△OAC的面积；‎ ‎（3）抛物线C2的对称轴为l，顶点为M，在（2）的条件下：‎ ‎①点P为抛物线C2对称轴l上一动点，当△PAC的周长最小时，求点P的坐标；‎ ‎②如图2，点E在抛物线C2上点O与点M之间运动，四边形OBCE的面积是否存在最大值？若存在，求出面积的最大值和点E的坐标；若不存在，请说明理由．‎ ‎　‎ ‎2017年四川省乐山市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项符合题目要求．‎ ‎1．（3分）（2017•乐山）﹣2的倒数是（　　）‎ A．﹣ B． C．2 D．﹣2‎ ‎【考点】17：倒数．‎ ‎【分析】根据乘积是1的两个数叫做互为倒数解答．‎ ‎【解答】解：∵（﹣2）×（﹣）=1，‎ ‎∴﹣2的倒数是﹣．‎ 故选A．‎ ‎【点评】本题考查了倒数的定义，是基础题，熟记概念是解题的关键．‎ ‎　‎ ‎2．（3分）（2017•乐山）随着经济发展，人民的生活水平不断提高，旅游业快速增长，2016年国民出境旅游超过120 000 000人次，将120 000 000用科学记数法表示为（　　）‎ A．1.2×109 B．12×107 C．0.12×109 D．1.2×108‎ ‎【考点】1I：科学记数法—表示较大的数．‎ ‎【专题】17 ：推理填空题．‎ ‎【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．‎ ‎【解答】解：120 000 000=1.2×108．‎ 故选：D．‎ ‎【点评】此题主要考查了用科学记数法表示较大的数，一般形式为a×10n ‎，其中1≤|a|＜10，确定a与n的值是解题的关键．‎ ‎　‎ ‎3．（3分）（2017•乐山）下列图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎【考点】R5：中心对称图形；P3：轴对称图形．‎ ‎【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．‎ ‎【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；‎ B、不是轴对称图形，是中心对称图形，故本选项错误；‎ C、既不是轴对称图形，也不是中心对称图形，故本选项错误；‎ D、既是轴对称图形又是中心对称图形，故本选项正确．‎ 故选D．‎ ‎【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．‎ ‎　‎ ‎4．（3分）（2017•乐山）含30°角的直角三角板与直线l1、l2的位置关系如图所示，已知l1∥l2，∠ACD=∠A，则∠1=（　　）‎ A．70° B．60° C．40° D．30°‎ ‎【考点】JA：平行线的性质．‎ ‎【分析】先根据三角形外角性质得到∠CDB的度数，再根据平行线的性质，即可得到∠1的度数．‎ ‎【解答】解：∵∠ACD=∠A=30°，‎ ‎∴∠CDB=∠A+∠ACD=60°，‎ ‎∵l1∥l2，‎ ‎∴∠1=∠CDB=60°，‎ 故选：B．‎ ‎【点评】本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．‎ ‎　‎ ‎5．（3分）（2017•乐山）下列说法正确的是（　　）‎ A．打开电视，它正在播广告是必然事件 B．要考察一个班级中的学生对建立生物角的看法适合用抽样调查 C．在抽样调查过程中，样本容量越大，对总体的估计就越准确 D．甲、乙两人射中环数的方差分别为S甲2=2，S乙2=4，说明乙的射击成绩比甲稳定 ‎【考点】X1：随机事件；V2：全面调查与抽样调查；V3：总体、个体、样本、样本容量；W7：方差．‎ ‎【分析】根据随机事件的概念、全面调查和抽样调查的关系、方差的性质判断即可．‎ ‎【解答】解：A、打开电视，它正在播广告是随机事件，A错误；‎ B、要考察一个班级中的学生对建立生物角的看法适合用全面调查，B错误；‎ C、在抽样调查过程中，样本容量越大，对总体的估计就越准确，C正确；‎ D、甲、乙两人射中环数的方差分别为S甲2=2，S乙2=4，说明甲的射击成绩比乙稳定，D错误；‎ 故选：C．‎ ‎【点评】本题考查的是随机事件、全面调查和抽样调查、方差，掌握随机事件的概念、全面调查和抽样调查的关系、方差的性质是解题的关键．‎ ‎　‎ ‎6．（3分）（2017•乐山）若a2﹣ab=0（b≠0），则=（　　）‎ A．0 B． C．0或 D．1或 2‎ ‎【考点】64：分式的值．‎ ‎【分析】首先求出a=0或a=b，进而求出分式的值．‎ ‎【解答】解：∵a2﹣ab=0（b≠0），‎ ‎∴a=0或a=b，‎ 当a=0时，=0．‎ 当a=b时，=，‎ 故选C．‎ ‎【点评】本题主要考查了分式的值，解题的关键是要注意题目有两个答案，容易漏掉值为0的情况．‎ ‎　‎ ‎7．（3分）（2017•乐山）如图是“明清影视城”的一扇圆弧形门，小红到影视城游玩，他了解到这扇门的相关数据：这扇圆弧形门所在的圆与水平地面是相切的，AB=CD=0.25米，BD=1.5米，且AB、CD与水平地面都是垂直的．根据以上数据，请你帮小红计算出这扇圆弧形门的最高点离地面的距离是（　　）‎ A．2米 B．2.5米 C．2.4米 D．2.1米 ‎【考点】M3：垂径定理的应用．‎ ‎【分析】连接OF，交AC于点E，设圆O的半径为R米，根据勾股定理列出方程，解方程即可．‎ ‎【解答】解：连接OF，交AC于点E，‎ ‎∵BD是⊙O的切线，‎ ‎∴OF⊥BD，‎ ‎∵四边形ABDC是矩形，‎ ‎∴AD∥BD，‎ ‎∴OE⊥AC，EF=AB，‎ 设圆O的半径为R，在Rt△AOE中，AE===0.75米，‎ OE=R﹣AB=R﹣0.25，‎ ‎∵AE2+OE2=OA2，‎ ‎∴0.752+（R﹣0.25）2=R2，‎ 解得R=1.25．‎ ‎1.25×2=2.5（米）．‎ 答：这扇圆弧形门的最高点离地面的距离是2.5米．‎ 故选：B．‎ ‎【点评】本题考查的是垂径定理的应用，掌握平分弦（不是直径）的直径垂直于弦是解题的关键，注意勾股定理的灵活运用．‎ ‎　‎ ‎8．（3分）（2017•乐山）已知x+=3，则下列三个等式：①x2+=7，②x﹣，③2x2﹣6x=﹣2中，正确的个数有（　　）‎ A．0个 B．1个 C．2个 D．3个 ‎【考点】4C：完全平方公式；6C：分式的混合运算．‎ ‎【分析】将x+=3两边同时平方，然后通过恒等变形可对①作出判断，由x﹣=±可对②作出判断，方程2x2﹣6x=﹣2两边同时除以2x，然后再通过恒等变形可对③作出判断．‎ ‎【解答】解：∵x+=3，‎ ‎∴（x+）2=9，整理得：x2+=7，故①正确．‎ x﹣=±=±，故②错误．‎ 方程2x2﹣6x=﹣2两边同时除以2x得：x﹣3=﹣，整理得：x+=3，故③正确．‎ 故选：C．‎ ‎【点评】本题主要考查的是完全平方公式的应用，熟练掌握完全平方公式是解题的关键．‎ ‎　‎ ‎9．（3分）（2017•乐山）已知二次函数y=x2﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（　　）‎ A． B． C．或 D．或 ‎【考点】H7：二次函数的最值．‎ ‎【分析】将二次函数配方成顶点式，分m＜﹣1、m＞2和﹣1≤m≤2三种情况，根据y的最小值为﹣2，结合二次函数的性质求解可得．‎ ‎【解答】解：y=x2﹣2mx=（x﹣m）2﹣m2，‎ ‎①若m＜﹣1，当x=﹣1时，y=1+2m=﹣2，‎ 解得：m=﹣；‎ ‎②若m＞2，当x=2时，y=4﹣4m=﹣2，‎ 解得：m=＜2（舍）；‎ ‎③若﹣1≤m≤2，当x=m时，y=﹣m2=﹣2，‎ 解得：m=或m=﹣＜﹣1（舍），‎ ‎∴m的值为﹣或，‎ 故选：D．‎ ‎【点评】本题主要考查二次函数的最值，根据二次函数的增减性分类讨论是解题的关键．‎ ‎　‎ ‎10．（3分）（2017•乐山）如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数y=的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（　　）‎ A． B． C． D． ‎【考点】G8：反比例函数与一次函数的交点问题；PB：翻折变换（折叠问题）．‎ ‎【分析】根据矩形的性质得到，CB∥x轴，AB∥y轴，于是得到D（6，1），E（，4），根据勾股定理得到ED==，连接BB′，交ED于F，过B′作B′G⊥BC于G，根据轴对称的性质得到BF=B′F，BB′⊥ED求得BB′=，设EG=x，则BG=﹣x根据勾股定理即可得到结论．‎ ‎【解答】解：∵矩形OABC，‎ ‎∴CB∥x轴，AB∥y轴，‎ ‎∵点B坐标为（6，4），‎ ‎∴D的横坐标为6，E的纵坐标为4，‎ ‎∵D，E在反比例函数y=的图象上，‎ ‎∴D（6，1），E（，4），‎ ‎∴BE=6﹣=，BD=4﹣1=3，‎ ‎∴ED==，‎ 连接BB′，交ED于F，过B′作B′G⊥BC于G，‎ ‎∵B，B′关于ED对称，‎ ‎∴BF=B′F，BB′⊥ED，‎ ‎∴BF•ED=BE•BD，‎ 即BF=3×，‎ ‎∴BF=，‎ ‎∴BB′=，‎ 设EG=x，则BG=﹣x，‎ ‎∵BB′2﹣BG2=B′G2=EB′2﹣GE2，‎ ‎∴（）2﹣（﹣x）2=（）2﹣x2，‎ ‎∴x=，‎ ‎∴EG=，‎ ‎∴CG=，‎ ‎∴B′G=，‎ ‎∴B′（，﹣），‎ ‎∴k=﹣．‎ 故选B．‎ ‎【点评】本题考查了翻折变换（折叠问题），矩形的性质，勾股定理，熟练掌握折叠的性质是解题的关键．‎ ‎　‎ 二、填空题：本大题共6小题，每小题3分，共18分．‎ ‎11．（3分）（2017•乐山）3﹣2=　　．‎ ‎【考点】6F：负整数指数幂．‎ ‎【专题】11 ：计算题．‎ ‎【分析】根据幂的负整数指数运算法则计算．‎ ‎【解答】解：原式==．‎ 故答案为：．‎ ‎【点评】本题考查的是幂的负整数指数运算，先把底数化成其倒数，然后将负整数指数幂当成正的进行计算．‎ ‎　‎ ‎12．（3分）（2017•乐山）二元一次方程组==x+2的解是　　．‎ ‎【考点】98：解二元一次方程组．‎ ‎【分析】根据二元一次方程组的解法即可求出答案．‎ ‎【解答】解：原方程可化为：，‎ 化简为，‎ 解得：．‎ 故答案为：；‎ ‎【点评】本题考查二元一次方程的解法，解题的关键是将原方程化为方程组，本题属于基础题型．‎ ‎　‎ ‎13．（3分）（2017•乐山）如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D．若OB=3，OD=2，则阴影部分的面积之和为　6　．‎ ‎【考点】R4：中心对称．‎ ‎【分析】根据中心对称图形的概念，以及长方形的面积公式即可解答．‎ ‎【解答】解：∵直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D，OB=3，OD=2，‎ ‎∴AB=2，‎ ‎∴阴影部分的面积之和为3×2=6．‎ 故答案为：6．‎ ‎【点评】此题主要考查了长方形的面积及中心对称图形的概念：在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．‎ ‎　‎ ‎14．（3分）（2017•乐山）点A、B、C在格点图中的位置如图5所示，格点小正方形的边长为1，则点C到线段AB所在直线的距离是　　．‎ ‎【考点】KQ：勾股定理．‎ ‎【分析】连接AC，BC，设点C到线段AB所在直线的距离是h，利用勾股定理求出AB的长，利用三角形的面积公式即可得出结论．‎ ‎【解答】解：连接AC，BC，设点C到线段AB所在直线的距离是h，‎ ‎∵S△ABC=3×3﹣×2×1﹣×2×1﹣×3×3﹣1=9﹣1﹣1﹣﹣1=，AB==，‎ ‎∴×h=，‎ ‎∴h=．‎ 故答案为：．‎ ‎【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．‎ ‎　‎ ‎15．（3分）（2017•乐山）庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言）：1=+++…++…．‎ 图2也是一种无限分割：在△ABC中，∠C=90°，∠B=30°，过点C作CC1⊥AB于点C1，再过点C1作C1C2⊥BC于点C2，又过点C2作C2C3⊥AB于点C3，如此无限继续下去，则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、…．假设AC=2，这些三角形的面积和可以得到一个等式是　2=　．‎ ‎【考点】38：规律型：图形的变化类．‎ ‎【分析】先根据AC=2，∠B=30°，CC1⊥AB，求得S△ACC1=；进而得到=×，=×（）2，=×（）3，根据规律可知=×（）n﹣1，再根据S△ABC=AC×BC=×2×2=2，即可得到等式．‎ ‎【解答】解：如图2，∵AC=2，∠B=30°，CC1⊥AB，‎ ‎∴Rt△ACC1中，∠ACC1=30°，且BC=2，‎ ‎∴AC1=AC=1，CC1=AC1=，‎ ‎∴S△ACC1=•AC1•CC1=×1×=；‎ ‎∵C1C2⊥BC，‎ ‎∴∠CC1C2=∠ACC1=30°，‎ ‎∴CC2=CC1=，C1C2=CC2=，‎ ‎∴=•CC2•C1C2=××=×，‎ 同理可得，‎ =×（）2，‎ =×（）3，‎ ‎…‎ ‎∴=×（）n﹣1，‎ 又∵S△ABC=AC×BC=×2×2=2，‎ ‎∴2=+×+×（）2+×（）3+…+×（）n﹣1+…‎ ‎∴2=．‎ 故答案为：2=．‎ ‎【点评】本题主要考查了图形的变化类问题，解决问题的关键是找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．探寻规律要认真观察、仔细思考，善用联想来解决这类问题．‎ ‎　‎ ‎16．（3分）（2017•乐山）对于函数y=xn+xm，我们定义y'=nxn﹣1+mxm﹣1（m、n为常数）．‎ 例如y=x4+x2，则y'=4x3+2x．‎ 已知：y=x3+（m﹣1）x2+m2x．‎ ‎（1）若方程y′=0有两个相等实数根，则m的值为　　；‎ ‎（2）若方程y′=m﹣有两个正数根，则m的取值范围为　且　．‎ ‎【考点】HA：抛物线与x轴的交点；AA：根的判别式；AB：根与系数的关系．‎ ‎【专题】23 ：新定义．‎ ‎【分析】根据新定义得到y′=x3+（m﹣1）x2+m2=x2﹣2（m﹣1）x+m2，‎ ‎（1）由判别式等于0，解方程即可；‎ ‎（2）根据根与系数的关系列不等式组即可得到结论．‎ ‎【解答】解：根据题意得y′=x2﹣2（m﹣1）x+m2，‎ ‎（1）∵方程x2﹣2（m﹣1）x+m2=0有两个相等实数根，‎ ‎∴△=[﹣2（m﹣1）]2﹣4m2=0，‎ 解得：m=，‎ 故答案为：；‎ ‎（2）y′=m﹣，即x2+2（m﹣1）x+m2=m﹣，‎ 化简得：x2+2（m﹣1）x+m2﹣m+=0，‎ ‎∵方程有两个正数根，‎ ‎∴，‎ 解得：且．‎ 故答案为：且．‎ ‎【点评】本题考查了抛物线与x轴的交点，根的判别式，根与系数的关系，正确的理解题意是解题的关键．‎ ‎　‎ 三、本大题共3小题，每小题9分，共27分.‎ ‎17．（9分）（2017•乐山）计算：2sni60°+|1﹣|+20170﹣．‎ ‎【考点】2C：实数的运算；6E：零指数幂．‎ ‎【专题】11 ：计算题．‎ ‎【分析】首先计算乘方、开方和乘法，然后从左向右依次计算，求出算式的值是多少即可．‎ ‎【解答】解：2sni60°+|1﹣|+20170﹣ ‎=2×+﹣1+1﹣3 ‎=﹣ ‎【点评】‎ 此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．‎ ‎　‎ ‎18．（9分）（2017•乐山）求不等式组的所有整数解．‎ ‎【考点】CC：一元一次不等式组的整数解．‎ ‎【分析】先求出不等式组的解集，再求出不等式组的整数解即可．‎ ‎【解答】解： 解不等式①得：x＞1，‎ 解不等式②得：x≤4，‎ 所以，不等式组的解集为1＜x≤4，‎ 故不等式组的整数解为2，3，4．‎ ‎【点评】本题考查了解一元一次不等式组和不等式组的整数解，能根据不等式的解集找出不等式组的解集是解此题的关键．‎ ‎　‎ ‎19．（9分）（2017•乐山）如图，延长▱ABCD的边AD到F，使DF=DC，延长CB到点E，使BE=BA，分别连结点A、E和C、F．求证：AE=CF．‎ ‎【考点】L5：平行四边形的性质．‎ ‎【分析】根据平行四边形的性质可得AD=BC，AD∥BC，再证出BE=DF，得出AF=EC，进而可得四边形AECF是平行四边形，从而可得AE=CF．‎ ‎【解答】证明：∵四边形ABCD是平行四边形，‎ ‎∴AD=BC，AD∥BC，‎ ‎∴AF∥EC，‎ ‎∵DF=DC，BE=BA，‎ ‎∴BE=DF，‎ ‎∴AF=EC，‎ ‎∴四边形AECF是平行四边形，‎ ‎∴AE=CF．‎ ‎【点评】此题主要考查了平行四边形的性质和判定，关键是掌握平行四边形对边平行且相等，一组对边平行且相等的四边形是平行四边形．‎ ‎　‎ 四、本大题共3小题，每小题10分，共30分．‎ ‎20．（10分）（2017•乐山）化简：（﹣）÷．‎ ‎【考点】6C：分式的混合运算．‎ ‎【分析】根据分式的减法和除法可以解答本题．‎ ‎【解答】解：（﹣）÷ ‎= ‎= ‎= ‎= ‎=．‎ ‎【点评】本题考查分式的混合运算，解答本题的关键是明确分式的混合运算的计算方法．‎ ‎　‎ ‎21．（10分）（2017•乐山）为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：‎ 组别 分数段（分）‎ 频数 频率 A组 ‎60≤x＜70‎ ‎30‎ ‎0.1‎ B组 ‎70≤x＜80‎ ‎90‎ n C组 ‎80≤x＜90‎ m ‎0.4‎ D组 ‎90≤x＜100‎ ‎60‎ ‎0.2‎ ‎（1）在表中：m=　120　，n=　0.3　；‎ ‎（2）补全频数分布直方图；‎ ‎（3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在　C　组；‎ ‎（4）4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明．‎ ‎【考点】X6：列表法与树状图法；V7：频数（率）分布表；V8：频数（率）分布直方图；W4：中位数．‎ ‎【分析】（1）先根据A组频数及其频率求得总人数，再根据频率=频数÷总人数可得m、n的值；‎ ‎（2）根据（1）中所求结果即可补全频数分布直方图；‎ ‎（3）根据中位数的定义即可求解；‎ ‎（4）画树状图列出所有等可能结果，再找到抽中A、C的结果，根据概率公式求解可得．‎ ‎【解答】解：（1）∵本次调查的总人数为30÷0.1=300（人），‎ ‎∴m=300×0.4=120，n=90÷300=0.3，‎ 故答案为：120，0.3；‎ ‎（2）补全频数分布直方图如下：‎ ‎（3）由于共有300个数据，则其中位数为第150、151个数据的平均数，‎ 而第150、151个数据的平均数均落在C组，‎ ‎∴据此推断他的成绩在C组，‎ 故答案为：C；‎ ‎（4）画树状图如下：‎ 由树状图可知，共有12种等可能结果，其中抽中A﹑C两组同学的有2种结果，‎ ‎∴抽中A﹑C两组同学的概率为=．‎ ‎【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题，也考查列表法或画树状图法求概率．‎ ‎　‎ ‎22．（10分）（2017•乐山）如图，在水平地面上有一幢房屋BC与一棵树DE，在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°，∠CAD=60°，在屋顶C处测得∠DCA=90°．若房屋的高BC=6米，求树高DE的长度．‎ ‎【考点】TA：解直角三角形的应用﹣仰角俯角问题．‎ ‎【分析】首先解直角三角形求得表示出AC，AD的长，进而利用直角三角函数，求出答案．‎ ‎【解答】解：如图3，在Rt△ABC中，∠CAB=45°，BC=6m，‎ ‎∴（m）；‎ 在Rt△ACD中，∠CAD=60°，‎ ‎∴（m）；‎ 在Rt△DEA中，∠EAD=60°，，‎ 答：树DE的高为米．‎ ‎【点评】此题主要考查了解直角三角形的应用，熟练应用锐角三角函数关系是解题关键．‎ ‎　‎ 五、本大题共2小题，每小题10分，共20分.‎ ‎23．（10分）（2017•乐山）某公司从2014年开始投入技术改进资金，经技术改进后，其产品的成本不断降低，具体数据如下表：‎ 年 度 ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ 投入技改资金x（万元）‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ 产品成本y（万元/件）‎ ‎7.2‎ ‎6‎ ‎4.5‎ ‎4‎ ‎（1）请你认真分析表中数据，从一次函数和反比例函数中确定哪一个函数能表示其变化规律，给出理由，并求出其解析式；‎ ‎（2）按照这种变化规律，若2017年已投入资金5万元．‎ ‎①预计生产成本每件比2016年降低多少万元？‎ ‎②若打算在2017年把每件产品成本降低到3.2万元，则还需要投入技改资金多少万元？（结果精确到0.01万元）．‎ ‎【考点】GA：反比例函数的应用．‎ ‎【分析】（1）根据实际题意和数据特点分情况求解，根据排除法可知其为反比例函数，利用待定系数法求解即可；‎ ‎（2）①直接把x=5万元代入函数解析式即可求解；‎ ‎②直接把y=3.2万元代入函数解析式即可求解；‎ ‎【解答】解：（1）设其为一次函数，解析式为y=kx+b，‎ 当x=2.5时，y=7.2；当x=3时，y=6，‎ ‎∴，‎ 解得k=﹣2.4，b=13.2‎ ‎∴一次函数解析式为y=﹣2.4x+13.2‎ 把x=4时，y=4.5代入此函数解析式，‎ 左边≠右边．‎ ‎∴其不是一次函数．‎ 同理．其也不是二次函数．‎ 设其为反比例函数．解析式为y=．‎ 当x=2.5时，y=7.2，可得：7.2=，‎ 解得k=18‎ ‎∴反比例函数是y=．‎ 验证：当x=3时，y==6，符合反比例函数．‎ 同理可验证x=4时，y=4.5，x=4.5时，y=4成立．‎ 可用反比例函数y=表示其变化规律．‎ ‎（2）①当x=5万元时，y=3.6．‎ ‎4﹣3.6=0.4（万元），‎ ‎∴生产成本每件比2009年降低0.4万元．‎ ‎②当y=3.2万元时，3.2=，‎ ‎∴x=5.625，‎ ‎∴5.625﹣4.5=1.125≈1.13（万元）‎ ‎∴还约需投入1.13万元．‎ ‎【点评】本题主要考查了反比例函数的应用．解题的关键是根据实际意义列出函数关系式，从实际意义中找到对应的变量的值，利用待定系数法求出函数解析式，再根据自变量的值求算对应的函数值．要注意用排除法确定函数的类型．‎ ‎　‎ ‎24．（10分）（2017•乐山）如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连结PC交AB于点E，且∠ACP=60°，PA=PD．‎ ‎（1）试判断PD与⊙O的位置关系，并说明理由；‎ ‎（2）若点C是弧AB的中点，已知AB=4，求CE•CP的值．‎ ‎【考点】S9：相似三角形的判定与性质；M4：圆心角、弧、弦的关系；MB：直线与圆的位置关系．‎ ‎【分析】（1）连结OP，根据圆周角定理可得∠AOP=2∠ACP=120°，然后计算出∠PAD和∠D的度数，进而可得∠OPD=90°，从而证明PD是⊙O的切线；‎ ‎（2）连结BC，首先求出∠CAB=∠ABC=∠APC=45°，然后可得AC长，再证明△CAE∽△CPA，进而可得，然后可得CE•CP的值．‎ ‎【解答】解：（1）如图，PD是⊙O的切线．‎ 证明如下：‎ 连结OP，‎ ‎∵∠ACP=60°，‎ ‎∴∠AOP=120°，‎ ‎∵OA=OP，‎ ‎∴∠OAP=∠OPA=30°，‎ ‎∵PA=PD，‎ ‎∴∠PAO=∠D=30°，‎ ‎∴∠OPD=90°，‎ ‎∴PD是⊙O的切线．‎ ‎（2）连结BC，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ACB=90°，‎ 又∵C为弧AB的中点，‎ ‎∴∠CAB=∠ABC=∠APC=45°，‎ ‎∵AB=4，．‎ ‎∵∠C=∠C，∠CAB=∠APC，‎ ‎∴△CAE∽△CPA，‎ ‎∴，‎ ‎∴CP•CE=CA2=（2）2=8．‎ ‎【点评】此题主要考查了切线的判定和相似三角形的性质和判定，关键是掌握切线的判定定理和相似三角形的判定与性质定理．‎ ‎　‎ 六、本大题共2小题，第25题12分，第26题13分，共25分.‎ ‎25．（12分）（2017•乐山）在四边形ABCD中，∠B+∠D=180°，对角线AC平分∠BAD．‎ ‎（1）如图1，若∠DAB=120°，且∠B=90°，试探究边AD、AB与对角线AC的数量关系并说明理由．‎ ‎（2）如图2，若将（1）中的条件“∠B=90°”去掉，（1）中的结论是否成立？请说明理由．‎ ‎（3）如图3，若∠DAB=90°，探究边AD、AB与对角线AC的数量关系并说明理由．‎ ‎【考点】LO：四边形综合题．‎ ‎【分析】（1）结论：AC=AD+AB，只要证明AD=AC，AB=AC即可解决问题；‎ ‎（2）（1）中的结论成立．以C为顶点，AC为一边作∠ACE=60°，∠ACE的另一边交AB延长线于点E，只要证明△DAC≌△BEC即可解决问题；‎ ‎（3）结论：．过点C作CE⊥AC交AB的延长线于点E，只要证明△ACE是等腰直角三角形，△DAC≌△BEC即可解决问题；‎ ‎【解答】解：（1）AC=AD+AB．‎ 理由如下：如图1中，‎ 在四边形ABCD中，∠D+∠B=180°，∠B=90°，‎ ‎∴∠D=90°，‎ ‎∵∠DAB=120°，AC平分∠DAB，‎ ‎∴∠DAC=∠BAC=60°，‎ ‎∵∠B=90°，‎ ‎∴，同理．‎ ‎∴AC=AD+AB．‎ ‎（2）（1）中的结论成立，理由如下：以C为顶点，AC为一边作∠ACE=60°，∠ACE的另一边交AB延长线于点E，‎ ‎∵∠BAC=60°，‎ ‎∴△AEC为等边三角形，‎ ‎∴AC=AE=CE，‎ ‎∵∠D+∠B=180°，∠DAB=120°，‎ ‎∴∠DCB=60°，‎ ‎∴∠DCA=∠BCE，‎ ‎∵∠D+∠ABC=180°，∠ABC+∠EBC=180°，‎ ‎∴∠D=∠CBE，∵CA=CB，‎ ‎∴△DAC≌△BEC，‎ ‎∴AD=BE，‎ ‎∴AC=AD+AB．‎ ‎（3）结论：．理由如下：‎ 过点C作CE⊥AC交AB的延长线于点E，∵∠D+∠B=180°，∠DAB=90°，‎ ‎∴DCB=90°，‎ ‎∵∠ACE=90°，‎ ‎∴∠DCA=∠BCE，‎ 又∵AC平分∠DAB，‎ ‎∴∠CAB=45°，‎ ‎∴∠E=45°．‎ ‎∴AC=CE．‎ 又∵∠D+∠B=180°，∠D=∠CBE，‎ ‎∴△CDA≌△CBE，‎ ‎∴AD=BE，‎ ‎∴AD+AB=AE．‎ 在Rt△ACE中，∠CAB=45°，‎ ‎∴，‎ ‎∴．‎ ‎【点评】本题考查四边形综合题、等边三角形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．‎ ‎　‎ ‎26．（13分）（2017•乐山）如图1，抛物线C1：y=x2+ax与C2：y=﹣x2+bx相交于点O、C，C1与C2分别交x轴于点B、A，且B为线段AO的中点．‎ ‎（1）求 的值；‎ ‎（2）若OC⊥AC，求△OAC的面积；‎ ‎（3）抛物线C2的对称轴为l，顶点为M，在（2）的条件下：‎ ‎①点P为抛物线C2对称轴l上一动点，当△PAC的周长最小时，求点P的坐标；‎ ‎②如图2，点E在抛物线C2上点O与点M之间运动，四边形OBCE的面积是否存在最大值？若存在，求出面积的最大值和点E的坐标；若不存在，请说明理由．‎ ‎【考点】HF：二次函数综合题．‎ ‎【分析】（1）由两抛物线解析式可分别用a和b表示出A、B两点的坐标，利用B为OA的中点可得到a和b之间的关系式；‎ ‎（2）由抛物线解析式可先求得C点坐标，过C作CD⊥x轴于点D，可证得△OCD∽△CAD，由相似三角形的性质可得到关于a的方程，可求得OA和CD的长，可求得△OAC的面积；‎ ‎（3）①连接OC与l的交点即为满足条件的点P，可求得OC的解析式，则可求得P点坐标；‎ ‎②设出E点坐标，则可表示出△EOB的面积，过点E作x轴的平行线交直线BC于点N，可先求得BC的解析式，则可表示出EN的长，进一步可表示出△EBC的面积，则可表示出四边形OBCE的面积，利用二次函数的性质可求得其最大值，及E点的坐标．‎ ‎【解答】解：‎ ‎（1）在y=x2+ax中，当y=0时，x2+ax=0，x1=0，x2=﹣a，‎ ‎∴B（﹣a，0），‎ 在y=﹣x2+bx中，当y=0时，﹣x2+bx=0，x1=0，x2=b，‎ ‎∴A（0，b），‎ ‎∵B为OA的中点，‎ ‎∴b=﹣2a，‎ ‎∴；‎ ‎（2）联立两抛物线解析式可得，消去y整理可得2x2+3ax=0，解得x1=0，，‎ 当时，，‎ ‎∴，‎ 过C作CD⊥x轴于点D，如图1，‎ ‎∴，‎ ‎∵∠OCA=90°，‎ ‎∴△OCD∽△CAD，‎ ‎∴，‎ ‎∴CD2=AD•OD，即，‎ ‎∴a1=0（舍去），（舍去），，‎ ‎∴，，‎ ‎∴；‎ ‎（3）①抛物线，‎ ‎∴其对称轴，‎ 点A关于l2的对称点为O（0，0），，‎ 则P为直线OC与l2的交点，‎ 设OC的解析式为y=kx，‎ ‎∴，得，‎ ‎∴OC的解析式为，‎ 当时，，‎ ‎∴；‎ ‎②设，‎ 则，‎ 而，，‎ 设直线BC的解析式为y=kx+b，‎ 由，解得，‎ ‎∴直线BC的解析式为，‎ 过点E作x轴的平行线交直线BC于点N，如图2，‎ 则，即x=，‎ ‎∴EN=，‎ ‎∴ ‎∴S四边形OBCE=S△OBE+S△EBC==，‎ ‎∵，‎ ‎∴当时，，‎ 当时，，‎ ‎∴，．‎ ‎【点评】本题为二次函数的综合应用，涉及待定系数法、相似三角形的判定和性质、轴对称的性质、三角形的面积、二次函数的性质及方程思想等知识．在（1）中分别表示出A、B的坐标是解题的关键，在（2）中求得C点坐标，利用相似三角形的性质求得a的值是解题的关键，在（3）①中确定出P点的位置是解题的关键，在（3）②中用E点坐标分别表示出△OBE和△‎ EBC的面积是解题的关键．本题考查知识点较多，综合性较强，计算量较大，难度较大．‎ ‎　‎