2008年海南省中考数学考试 7页

海南省2008年初中毕业生学业考试 数 学 科 试 题 ‎（考试时间100分钟，满分110分）‎ 特别提醒：‎ ‎1.选择题用2B铅笔填涂，其余答案一律用黑色笔填写在答题卡上，写在试题卷上无效.‎ ‎2.答题前请认真阅读试题及有关说明.‎ ‎3.请合理安排好答题时间.‎ 一、 选择题（本大题满分20分，每小题2分）‎ 在下列各题的四个备选答案中，只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑.‎ 1. 在0，-2，1，这四个数中，最小的数是（ ）‎ A. 0 B. ‎-2 ‎‎ C. 1 D. ‎ ‎2. 数据26000用科学记数法表示为2.6×10n，则n的值是（ ）‎ A. 2 B. ‎3 C. 4 D. 5‎ ‎3. 下列运算，正确的是（ ）‎ A. B. C. D. ‎ 4. 观察下列几何体，主视图、左视图和俯视图都是矩形的是（ ）‎ A B D C ‎ ‎ ‎5. 如图1，AB、CD相交于点O，∠1=80°，如果DE∥AB，那么∠D的度数为（ ）‎ A. 80° B. 90° C. 100° D. 110°‎ F E D B C ‎60°‎ 图2‎ A A B C O E ‎1‎ D 图1‎ ‎6. 如图2所示，Rt△ABC∽Rt△DEF，则cosE的值等于（ ）‎ A. B. C. D. ‎ ‎7. 不等式组的解集是（ ）‎ A. x＞-1 B. x≤‎1 C. x＜-1 D. -1＜x≤1‎ A B O C 图3‎ ‎45°‎ 8. 如图3，AB是⊙O的直径，AC是⊙O的切线，A为切点，‎ 连接BC，若∠ABC=45°，则下列结论正确的是（ ）‎ A. AC＞AB B. AC=AB ‎ C. AC＜AB D. AC=BC ‎9. 如图4，直线l1和l2的交点坐标为（ ）‎ A.(4,-2) B. (2,-4) C. (-4,2) D. (3,-1)‎ ‎90‎ ‎85‎ ‎80‎ ‎75‎ ‎70‎ ‎65‎ ‎60‎ ‎55‎ 分数 测验1‎ 测验2‎ 测验3‎ 测验4‎ 测验5‎ 测验6‎ 图5‎ 图4‎ O y x ‎2‎ ‎2‎ l1‎ l2‎ ‎10.图5是小敏同学6次数学测验的成绩统计表，则该同学6次成绩的中位数是（ ）‎ A. 60分 B. 70分 C.75分 D. 80分 二、填空题（本大题满分24分，每小题3分）‎ 11.计算： .‎ ‎12.方程的解是 .‎ ‎13.反比例函数的图象经过点(-2,1)，则k的值为 .‎ ‎14.随机掷一枚质地均匀的普通硬币两次,出现两次正面都朝上的概率是 .‎ ‎15.用同样大小的黑色棋子按图6所示的方式摆图形，按照这样的规律摆下去，则第n个图形需棋子 枚（用含n的代数式表示）.‎ 第1个图 第2个图 第3个图 ‎…‎ 图6‎ ‎16. 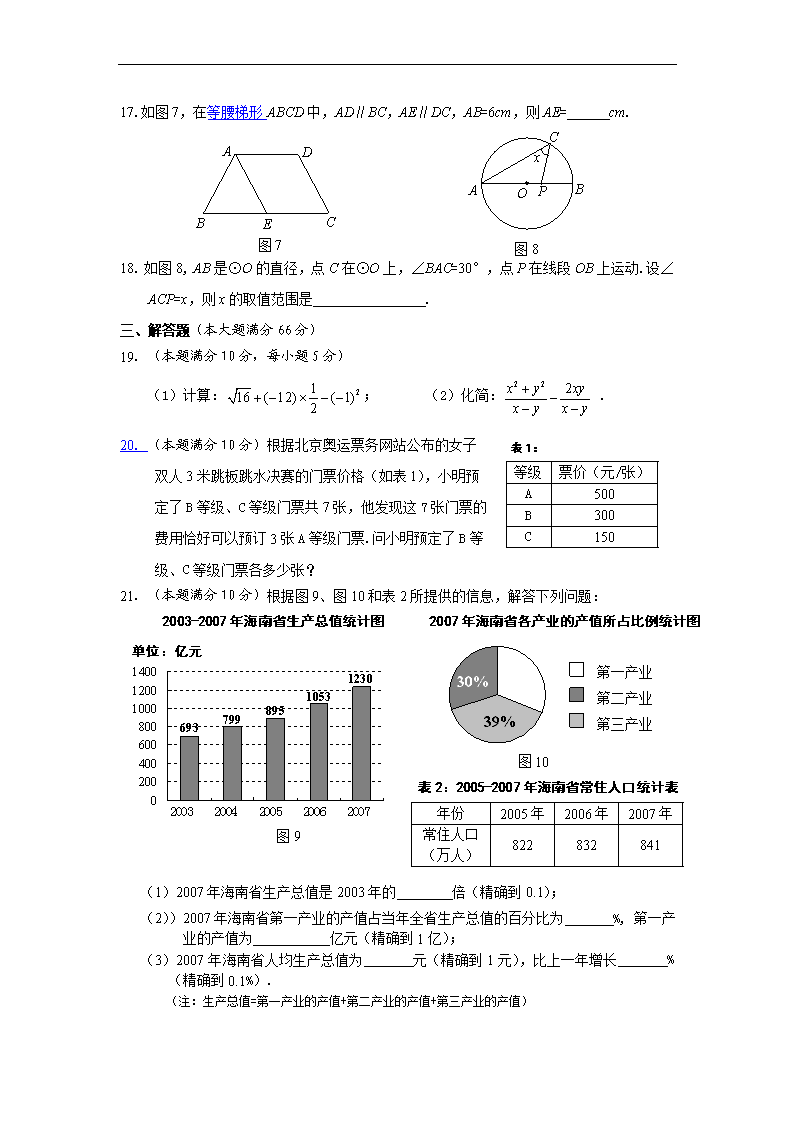已知在△ABC和△A1B‎1C1中，AB=A1B1，∠A=∠A1，要使△ABC≌△A1B‎1C1，还需添加一个条件，这个条件可以是 .‎ 图8‎ A B O C x P ‎17.如图7，在等腰梯形ABCD中，AD∥BC，AE∥DC，AB=‎6cm，则AE= cm.‎ A B C 图7‎ E D ‎18. 如图8, AB是⊙O的直径，点C在⊙O上，∠BAC=30°，点P在线段OB上运动.设∠ACP=x，则x的取值范围是 .‎ 三、解答题（本大题满分66分）‎ ‎19. （本题满分10分，每小题5分）‎ ‎（1）计算：； （2）化简： . ‎ 表1：‎ 等级 票价（元/张）‎ A ‎500‎ B ‎300‎ C ‎150‎ 20. （本题满分10分）根据北京奥运票务网站公布的女子 双人‎3米跳板跳水决赛的门票价格（如表1），小明预 定了B等级、C等级门票共7张，他发现这7张门票的 费用恰好可以预订3张A等级门票.问小明预定了B等 级、C等级门票各多少张？‎ ‎21. （本题满分10分）根据图9、图10和表2所提供的信息，解答下列问题：‎ ‎2003-2007年海南省生产总值统计图 单位：亿元 图9‎ ‎2003年 ‎2004年 ‎2005年 ‎2006年 ‎2007年 ‎2007年海南省各产业的产值所占比例统计图 ‎39%‎ ‎30%‎ 第一产业 第二产业 第三产业 图10‎ 表2：2005-2007年海南省常住人口统计表 年份 ‎2005年 ‎2006年 ‎2007年 常住人口 ‎（万人）‎ ‎822‎ ‎832‎ ‎841‎ ‎（1）2007年海南省生产总值是2003年的 倍（精确到0.1）；‎ ‎（2））2007年海南省第一产业的产值占当年全省生产总值的百分比为 %, 第一产业的产值为 亿元（精确到1亿）；‎ ‎（3）2007年海南省人均生产总值为 元（精确到1元），比上一年增长 %（精确到0.1%）.‎ ‎（注：生产总值=第一产业的产值+第二产业的产值+第三产业的产值）‎ O y x P A B C ‎•‎ B1‎ A1‎ C1‎ ‎1‎ ‎1‎ 图11‎ ‎22. （本题满分10分）如图11，在平面直角坐标系中，△ABC和△A1B‎1C1关于点E成中心对称.‎ ‎（1）画出对称中心E，并写出点E、A、C的坐标；‎ ‎（2）P(a,b)是△ABC的边AC上一点，△ABC经 平移后点P的对应点为P2(a+6, b+2)，请画出 上述平移后的△A2B‎2C2，并写出点A2、C2的坐 标；‎ ‎（3）判断△A2B‎2C2和△A1B‎1C1的位置关系（直接写 出结果）.‎ ‎23．（本题满分12分）如图12，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB.‎ ‎（1）求证：① PE=PD ； ② PE⊥PD；‎ ‎（2）设AP=x, △PBE的面积为y.‎ ‎① 求出y关于x的函数关系式，并写出x的取值范围；‎ A B C O D E x y x=2‎ 图13‎ ‎② 当x取何值时，y取得最大值，并求出这个最大值.‎ ‎ ‎ A B C P D E 图12‎ ‎24. （本题满分14分）如图13，已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C，直线y=-2x-1经过抛物线上一点B(-2,m)，且与y轴、直线x=2分别交于点D、E.‎ ‎（1）求m的值及该抛物线对应的函数关系式；‎ ‎（2）求证：① CB=CE ；② D是BE的中点；‎ ‎（3）若P(x，y)是该抛物线上的一个动点，是否存在这样的点P,使得PB=PE,若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由.‎ 海南省2008年初中毕业生学业考试 数学科试题参考答案及评分标准 一、选择题（本题满分20分，每小题2分）‎ ‎1． B 2．C 3．D 4．B 5．C 6．A 7．D 8．B 9．A 10. C 二、填空题（本题满分24分，每小题3分）‎ ‎11. 12. , 13. -2 14. 15. 3n+1 ‎ ‎16. 答案不唯一（如：∠B=∠B1，∠C=∠C1，AC=A‎1C1） 17. 6 18. 30°≤x≤90°‎ 三、解答题（本题满分66分）‎ 19．（1）原式= ‎4-6-1‎ ………（3分） （2）原式 ………（7分）‎ ‎ =-3 ………（5分） ………（9分）‎ ‎ =x-y. ………（10分）‎ ‎20. 设小明预订了B等级，C等级门票分别为x张和y张. ……………………（1分）‎ 依题意，得 ………………………………（6分）‎ 解这个方程组得 ………………………………（9分）‎ ‎·‎ E O y x P A B C ‎•‎ A2‎ B2‎ C2‎ B1‎ A1‎ C1‎ ‎1‎ ‎1‎ 答：小明预订了B等级门票3张，C等级门票4张. …………………………（10分）‎ 21．（1）1.8；（2）31，381；（3）14625，15.6 ……（10分）‎ ‎22．（1）如图，E(-3，-1)，A(-3，2)，C(-2，0)；……（4分）‎ ‎（2）如图，A2(3，4)，C2(4，2)； ………（8分）‎ ‎（3）△A2B‎2C2与△A1B‎1C1关于原点O成中心对称.（10分）‎ 23. （1）证法一：‎ ‎① ∵ 四边形ABCD是正方形，AC为对角线，‎ ‎∴ BC=DC, ∠BCP=∠DCP=45°. ………………………………（1分）‎ ‎∵ PC=PC，‎ ‎∴ △PBC≌△PDC （SAS）. ………………………………（2分）‎ ‎∴ PB= PD， ∠PBC=∠PDC. ………………………………（3分）‎ 又∵ PB= PE ，‎ ‎∴ PE=PD. ………………………………（4分）‎ ‎ ② （i）当点E在线段BC上(E与B、C不重合)时，‎ ‎∵ PB=PE，‎ ‎∴ ∠PBE=∠PEB，‎ ‎∴ ∠PEB=∠PDC，‎ ‎∴ ∠PEB+∠PEC=∠PDC+∠PEC=180°，‎ ‎∴ ∠DPE=360°-(∠BCD+∠PDC+∠PEC)=90°，‎ ‎∴ PE⊥PD. ………………………………（6分）‎ A B C D P E ‎1‎ ‎2‎ H ‎（ii）当点E与点C重合时，点P恰好在AC中点处，此时，PE⊥PD.‎ ‎（iii）当点E在BC的延长线上时，如图.‎ ‎∵ ∠PEC=∠PDC，∠1=∠2，‎ ‎∴ ∠DPE=∠DCE=90°，‎ ‎∴ PE⊥PD.‎ 综合（i）（ii）（iii）, PE⊥PD. ………（7分）‎ A B C P D E F ‎（2）① 过点P作PF⊥BC，垂足为F，则BF=FE.‎ ‎∵ AP=x，AC=，‎ ‎∴ PC=- x，PF=FC=.‎ ‎ BF=FE=1-FC=1-()=.‎ ‎∴ S△PBE=BF·PF=(). …………………（9分）‎ 即 (0＜x＜). ………………………………（10分）‎ ‎② . ………………………………（11分）‎ ‎∵ ＜0，‎ ‎∴ 当时，y最大值. ………………………………（12分）‎ ‎（1）证法二：A B C P D E F G ‎1‎ ‎2‎ ‎3‎ ① 过点P作GF∥AB，分别交AD、BC于G、F. 如图所示.‎ ‎∵ 四边形ABCD是正方形，‎ ‎∴ 四边形ABFG和四边形GFCD都是矩形，‎ ‎△AGP和△PFC都是等腰直角三角形.‎ ‎ ∴ GD=FC=FP，GP=AG=BF，∠PGD=∠PFE=90°.‎ ‎ 又∵ PB=PE，‎ ‎ ∴ BF=FE，‎ ‎ ∴ GP=FE，‎ ‎∴ △EFP≌△PGD （SAS）. ………………………………（3分）‎ ‎∴ PE=PD. ………………………………（4分）‎ ‎② ∴ ∠1=∠2.‎ ‎∴ ∠1+∠3=∠2+∠3=90°.‎ ‎∴ ∠DPE=90°.‎ ‎∴ PE⊥PD. ………………………………（7分）‎ ‎（2）①∵ AP=x，‎ ‎ ∴ BF=PG=，PF=1-. ………………………………（8分）‎ ‎∴ S△PBE=BF·PF=(). …………………（9分）‎ 即 (0＜x＜). ………………………………（10分）‎ ‎② . ………………………………（11分）‎ ‎∵ ＜0，‎ ‎∴ 当时，y最大值. ………………………………（12分）‎ ‎(注：用其它方法求解参照以上标准给分.)‎ 24.（1）∵ 点B(-2,m)在直线y=-2x-1上，‎ ‎∴ m=-2×(-2)-1=3. ………………………………（2分）‎ ‎∴ B(-2,3)‎ ‎∵ 抛物线经过原点O和点A，对称轴为x=2，‎ ‎∴ 点A的坐标为(4,0) . ‎ 设所求的抛物线对应函数关系式为y=a(x-0)(x-4). ……………………（3分）‎ 将点B(-2,3)代入上式，得3=a(-2-0)(-2-4)，∴ .‎ ‎∴ 所求的抛物线对应的函数关系式为，即. （6分）‎ ‎ （2）①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1) E(2,-5).‎ ‎ 过点B作BG∥x轴，与y轴交于F、直线x=2交于G，‎ A B C O D E x y x=2‎ G F H ‎ 则BG⊥直线x=2，BG=4.‎ ‎ 在Rt△BGC中，BC=.‎ ‎∵ CE=5，‎ ‎∴ CB=CE=5. ……………………（9分）‎ ‎②过点E作EH∥x轴，交y轴于H，‎ 则点H的坐标为H(0,-5).‎ 又点F、D的坐标为F(0,3)、D(0,-1)，‎ ‎∴ FD=DH=4，BF=EH=2，∠BFD=∠EHD=90°.‎ ‎ ∴ △DFB≌△DHE （SAS），‎ ‎∴ BD=DE.‎ 即D是BE的中点. ………………………………（11分）‎ ‎ （3） 存在. ………………………………（12分）‎ ‎ 由于PB=PE，∴ 点P在直线CD上，‎ ‎∴ 符合条件的点P是直线CD与该抛物线的交点.‎ ‎ 设直线CD对应的函数关系式为y=kx+b.‎ ‎ 将D(0,-1) C(2,0)代入，得. 解得 .‎ ‎ ∴ 直线CD对应的函数关系式为y=x-1.‎ ‎∵ 动点P的坐标为(x，)，‎ ‎∴ x-1=. ………………………………（13分）‎ 解得 ，. ∴ ，.‎ ‎∴ 符合条件的点P的坐标为(，)或(，).…（14分）‎ ‎(注：用其它方法求解参照以上标准给分.)‎