中考数学专题复习试卷分类汇编解析版直角三角形与勾股定理 36页

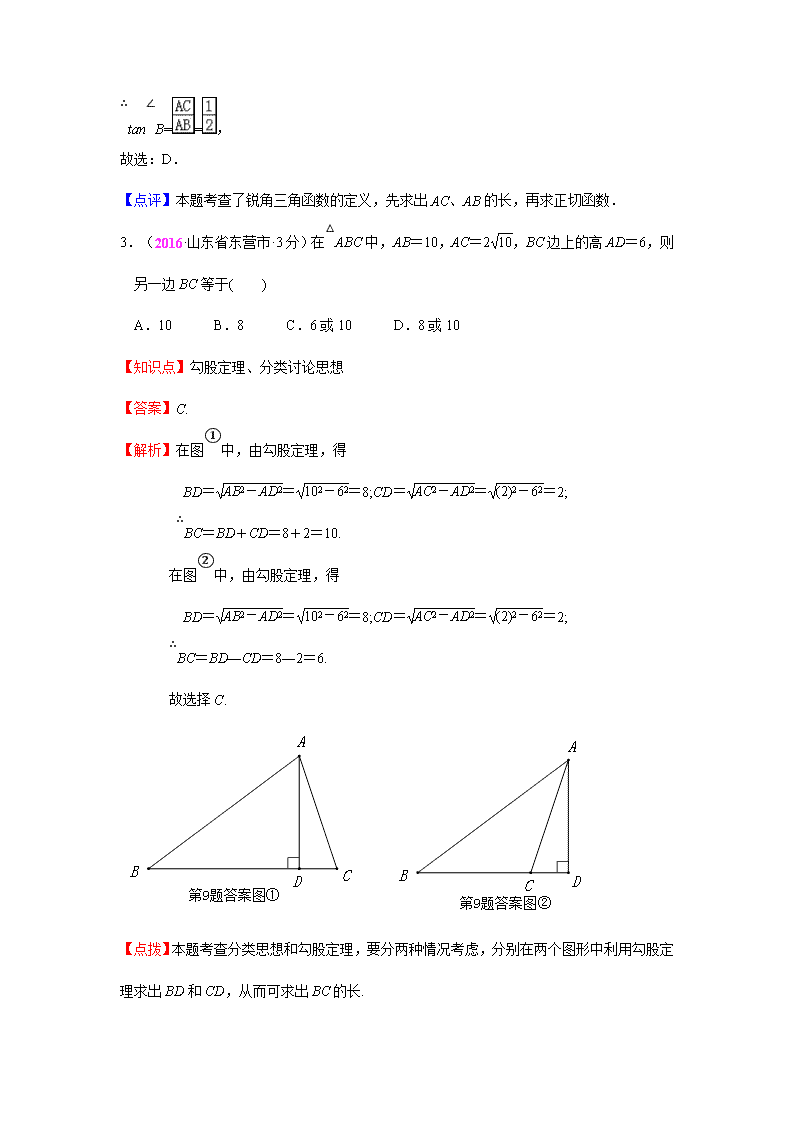
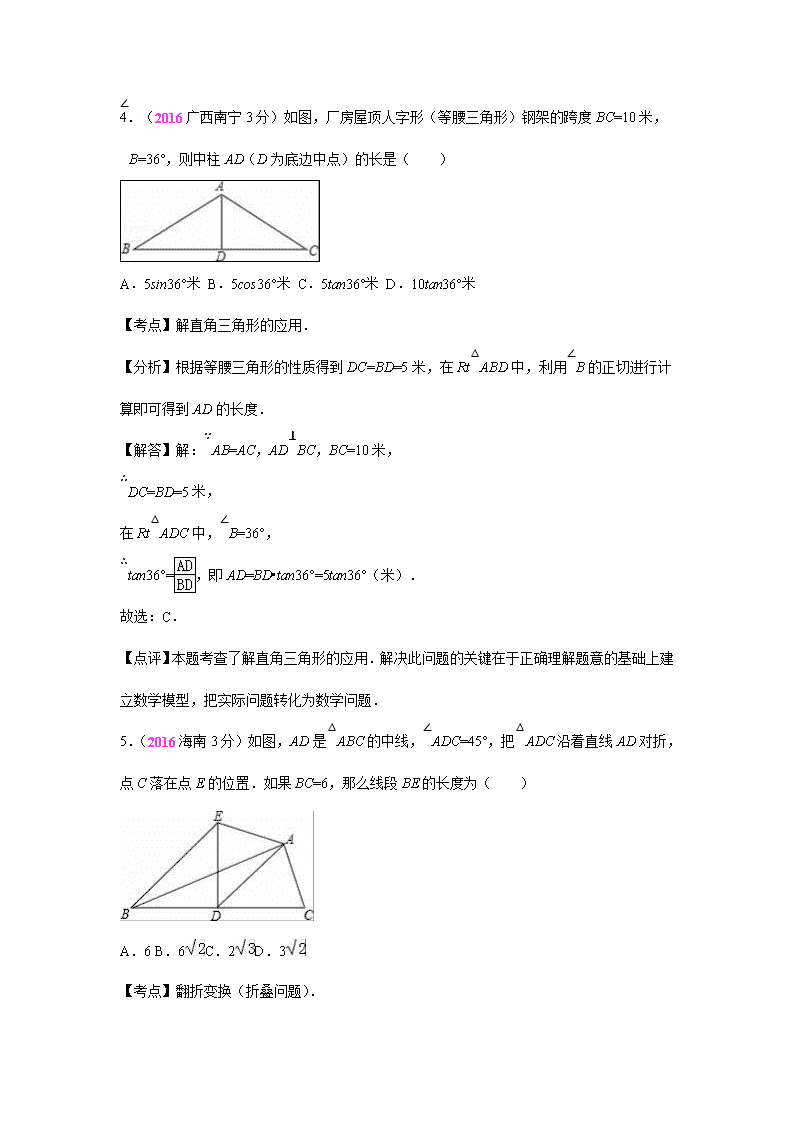
直角三角形与勾股定理 一、 ‎ 选择题 ‎1.（2016·广西百色·3分）如图，△ABC中，∠C=90°，∠A=30°，AB=12，则BC=（　　）‎ A．6 B．6C．6D．12‎ ‎【考点】含30度角的直角三角形．‎ ‎【分析】根据30°所对的直角边等于斜边的一半求解．‎ ‎【解答】解：∵∠C=90°，∠A=30°，AB=12，‎ ‎∴BC=12sin30°=12×=6，‎ 故答选A．‎ ‎2.（2016·贵州安顺·3分）如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是（　　）‎ A．2B． C． D．‎ ‎【分析】根据勾股定理，可得AC、AB的长，根据正切函数的定义，可得答案．‎ ‎【解答】解：如图：，‎ 由勾股定理，得 AC=，AB=2，BC=，‎ ‎∴△ABC为直角三角形，‎ ‎∴tan∠B==，‎ 故选：D．‎ ‎【点评】本题考查了锐角三角函数的定义，先求出AC、AB的长，再求正切函数．‎ ‎3．（2016·山东省东营市·3分）在△ABC中，AB＝10，AC＝2，BC边上的高AD＝6，则另一边BC等于( )‎ A．10　　　B．8　　　C．6或10　　　D．8或10‎ ‎【知识点】勾股定理、分类讨论思想 ‎【答案】C.‎ ‎【解析】在图①中，由勾股定理，得 BD＝＝＝8;CD＝＝＝2;‎ ‎∴BC＝BD＋CD＝8＋2＝10. ‎ 在图②中，由勾股定理，得 BD＝＝＝8;CD＝＝＝2;‎ ‎∴BC＝BD―CD＝8―2＝6.‎ 故选择C.‎ ‎【点拨】本题考查分类思想和勾股定理，要分两种情况考虑，分别在两个图形中利用勾股定理求出BD和CD，从而可求出BC的长.‎ ‎4．（2016广西南宁3分）如图，厂房屋顶人字形（等腰三角形）钢架的跨度BC=‎10米，∠B=36°，则中柱AD（D为底边中点）的长是（　　）‎ A．5sin36°米 B．5cos36°米 C．5tan36°米 D．10tan36°米 ‎【考点】解直角三角形的应用．‎ ‎【分析】根据等腰三角形的性质得到DC=BD=‎5米，在Rt△ABD中，利用∠B的正切进行计算即可得到AD的长度．‎ ‎【解答】解：∵AB=AC，AD⊥BC，BC=‎10米，‎ ‎∴DC=BD=‎5米，‎ 在Rt△ADC中，∠B=36°，‎ ‎∴tan36°=，即AD=BD•tan36°=5tan36°（米）．‎ 故选：C．‎ ‎【点评】本题考查了解直角三角形的应用．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．‎ ‎5．（2016海南3分）如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（　　）‎ A．6 B．6C．2D．3‎ ‎【考点】翻折变换（折叠问题）．‎ ‎【分析】根据折叠的性质判定△EDB是等腰直角三角形，然后再求BE．‎ ‎【解答】解：根据折叠的性质知，CD=ED，∠CDA=∠ADE=45°，‎ ‎∴∠CDE=∠BDE=90°，‎ ‎∵BD=CD，BC=6，‎ ‎∴BD=ED=3，‎ 即△EDB是等腰直角三角形，‎ ‎∴BE=BD=×3=3，‎ 故选D．‎ ‎【点评】本题考查了翻折变换，还考查的知识点有两个：1、折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；2、等腰直角三角形的性质求解．‎ ‎6. （2016·陕西·3分）如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（　　）‎ A．7 B．8 C．9 D．10‎ ‎【考点】三角形中位线定理；等腰三角形的判定与性质；勾股定理．‎ ‎【分析】根据三角形中位线定理求出DE，得到DF∥BM，再证明EC=EF=AC，由此即可解决问题．‎ ‎【解答】解：在RT△ABC中，∵∠ABC=90°，AB=8，BC=6，‎ ‎∴AC===10，‎ ‎∵DE是△ABC的中位线，‎ ‎∴DF∥BM，DE=BC=3，‎ ‎∴∠EFC=∠FCM，‎ ‎∵∠FCE=∠FCM，‎ ‎∴∠EFC=∠ECF，‎ ‎∴EC=EF=AC=5，‎ ‎∴DF=DE+EF=3+5=8．‎ 故选B．‎ ‎7. （2016·四川眉山·3分）把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是（　　）‎ A． B．6 C． D．‎ ‎【分析】由边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，利用勾股定理的知识求出BC′的长，再根据等腰直角三角形的性质，勾股定理可求BO，OD′，从而可求四边形ABOD′的周长．‎ ‎【解答】解：连接BC′，‎ ‎∵旋转角∠BAB′=45°，∠BAD′=45°，‎ ‎∴B在对角线AC′上，‎ ‎∵B′C′=AB′=3，‎ 在Rt△AB′C′中，AC′==3，‎ ‎∴B′C=3﹣3，‎ 在等腰Rt△OBC′中，OB=BC′=3﹣3，‎ 在直角三角形OBC′中，OC=（3﹣3）=6﹣3，‎ ‎∴OD′=3﹣OC′=3﹣3，‎ ‎∴四边形ABOD′的周长是：2AD′+OB+OD′=6+3﹣3+3﹣3=6．‎ 故选：A．‎ ‎【点评】本题考查了旋转的性质、正方形的性质以及等腰直角三角形的性质．此题难度适中，注意连接BC′构造等腰Rt△OBC′是解题的关键，注意旋转中的对应关系．‎ ‎8. （2016·四川南充）如图，在Rt△ABC中，∠A=30°，BC=1，点D，E分别是直角边BC，AC的中点，则DE的长为（　　） ‎ ‎ ‎ A．1 B．2 C． D．1+‎ ‎【分析】由“30度角所对的直角边等于斜边的一半”求得AB=2BC=2．然后根据三角形中位线定理求得DE=AB． ‎ ‎【解答】解：如图，∵在Rt△ABC中，∠C=90°，∠A=30°， ‎ ‎∴AB=2BC=2． ‎ 又∵点D、E分别是AC、BC的中点， ‎ ‎∴DE是△ACB的中位线， ‎ ‎∴DE=AB=1． ‎ 故选：A． ‎ ‎【点评】此题考查的是三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半． ‎ ‎9．（2016·四川内江）已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三边的距离之和为( )‎ A． B． C． D．不能确定 ‎[答案]B ‎[考点]勾股定理，三角形面积公式，应用数学知识解决问题的能力。‎ ‎[解析]如图，△ABC是等边三角形，AB＝3，点P是三角形内任意一点，过点P分别向三边AB，BC，CA作垂线，垂足依次为D，E，F，过点A作AH⊥BC于H．则 BH＝，AH＝＝．‎ 连接PA，PB，PC，则S△PAB＋S△PBC＋S△PCA＝S△ABC．‎ ‎∴AB·PD＋BC·PE＋CA·PF＝BC·AH．‎ ‎∴PD＋PE＋PF＝AH＝．‎ 故选B．‎ P B A D E F 答案图 C H ‎10．（2016·四川宜宾）如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为（　　）‎ A． B．2C．3 D．2‎ ‎【考点】旋转的性质．‎ ‎【分析】通过勾股定理计算出AB长度，利用旋转性质求出各对应线段长度，利用勾股定理求出B、D两点间的距离．‎ ‎【解答】解：∵在△ABC中，∠C=90°，AC=4，BC=3，‎ ‎∴AB=5，‎ ‎∵将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，‎ ‎∴AE=4，DE=3，‎ ‎∴BE=1，‎ 在Rt△BED中，‎ BD==．‎ 故选：A．‎ ‎11.（2016·黑龙江龙东·3分）若点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，则△ABC的面积为（　　）‎ A．2+B． C．2+或2﹣D．4+2或2﹣‎ ‎【考点】三角形的外接圆与外心；等腰三角形的性质．‎ ‎【分析】根据题意可以画出相应的图形，然后根据不同情况，求出相应的边的长度，从而可以求出不同情况下△ABC的面积，本题得以解决．‎ ‎【解答】解：由题意可得，如右图所示，‎ 存在两种情况，‎ 当△ABC为△A1BC时，连接OB、OC，‎ ‎∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，‎ ‎∴△OBC为等边三角形，OB=OC=BC=2，OA1⊥BC于点D，‎ ‎∴CD=1，OD=，‎ ‎∴=2﹣，‎ 当△ABC为△A2BC时，连接OB、OC，‎ ‎∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，‎ ‎∴△OBC为等边三角形，OB=OC=BC=2，OA1⊥BC于点D，‎ ‎∴CD=1，OD=，‎ ‎∴S△A2BC===2+，‎ 由上可得，△ABC的面积为或2+，‎ 故选C．‎ ‎12．（2016·湖北荆门·3分）如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（　　）‎ A．5 B．6 C．8 D．10‎ ‎【考点】勾股定理；等腰三角形的性质．‎ ‎【分析】根据等腰三角形的性质得到AD⊥BC，BD=CD，根据勾股定理即可得到结论．‎ ‎【解答】解：∵AB=AC，AD是∠BAC的平分线，‎ ‎∴AD⊥BC，BD=CD，‎ ‎∵AB=5，AD=3，‎ ‎∴BD==4，‎ ‎∴BC=2BD=8，‎ 故选C．‎ ‎13．（2016·湖北荆州·3分）如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（　　）‎ A．2 B． C． D．‎ ‎【分析】先根据勾股定理的逆定理判断出△ABC的形状，再由锐角三角函数的定义即可得出结论．‎ ‎【解答】解：∵由图可知，AC2=22+42=20，BC2=12+22=5，AB2=32+42=25，‎ ‎∴△ABC是直角三角形，且∠ACB=90°，‎ ‎∴cos∠ABC==．‎ 故选D．‎ ‎【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．‎ 一、 填空题 ‎1. （2016·浙江省湖州市·4分）如图，在Rt△ABC中，∠ACB=90°，BC=6，AC=8，分别以点A，B为圆心，大于线段AB长度一半的长为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连结CD，则CD的长是　5　．‎ ‎【考点】作图—基本作图；直角三角形斜边上的中线；勾股定理．‎ ‎【分析】首先说明AD=DB，利用直角三角形斜边中线等于斜边一半，即可解决问题．‎ ‎【解答】解：由题意EF是线段AB的垂直平分线，‎ ‎∴AD=DB，‎ Rt△ABC中，∵∠ACB=90°，BC=6，AC=8，‎ ‎∴AB===10，‎ ‎∵AD=DB，∠ACB=90°，‎ ‎∴CD=AB=5．‎ 故答案为5．‎ ‎2. （2016·湖北随州·3分）如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=BD，连接DM、DN、MN．若AB=6，则DN=　3　．‎ ‎【考点】三角形中位线定理；直角三角形斜边上的中线；平行四边形的判定与性质．‎ ‎【分析】连接CM，根据三角形中位线定理得到NM=CB，MN∥BC，证明四边形DCMN是平行四边形，得到DN=CM，根据直角三角形的性质得到CM=AB=3，等量代换即可．‎ ‎【解答】解：连接CM，‎ ‎∵M、N分别是AB、AC的中点，‎ ‎∴NM=CB，MN∥BC，又CD=BD，‎ ‎∴MN=CD，又MN∥BC，‎ ‎∴四边形DCMN是平行四边形，‎ ‎∴DN=CM，‎ ‎∵∠ACB=90°，M是AB的中点，‎ ‎∴CM=AB=3，‎ ‎∴DN=3，‎ 故答案为：3．‎ ‎3. （2016·湖北武汉·3分）如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝10，DA＝，则BD的长为_______．‎ ‎【考点】相似三角形，勾股定理 ‎【答案】2‎ ‎【解析】连接AC，过点D作BC边上的高，交BC延长线于点H．在Rt△ABC中，AB＝3，BC＝4，∴AC＝5，又CD＝10，DA＝，可知△ACD为直角三角形，且∠ACD＝90°，易证△ABC∽△CHD，则CH＝6，DH＝8，∴BD＝．‎ ‎4. （2016·江西·3分）如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是　5sqrt{2}或4sqrt{5}或5　．‎ ‎【考点】矩形的性质；等腰三角形的性质；勾股定理．‎ ‎【分析】分情况讨论：①当AP=AE=5时，则△AEP是等腰直角三角形，得出底边PE=AE=5即可；‎ ‎②当PE=AE=5时，求出BE，由勾股定理求出PB，再由勾股定理求出等边AP即可；‎ ‎③当PA=PE时，底边AE=5；即可得出结论．‎ ‎【解答】解：如图所示：‎ ‎①当AP=AE=5时，‎ ‎∵∠BAD=90°，‎ ‎∴△AEP是等腰直角三角形，‎ ‎∴底边PE=AE=5；‎ ‎②当PE=AE=5时，‎ ‎∵BE=AB﹣AE=8﹣5=3，∠B=90°，‎ ‎∴PB==4，‎ ‎∴底边AP===4；‎ ‎③当PA=PE时，底边AE=5；‎ 综上所述：等腰三角形AEP的对边长为5或4或5；‎ 故答案为：5或4或5．‎ ‎5. （2016·四川内江）如图4，在菱形ABCD中，对角线AC与BD相交于点O，AC＝8，BD＝6，OE⊥BC，垂足为点E，则OE＝______．‎ D O C E B A 图4‎ ‎[答案]‎ ‎[考点]菱形的性质，勾股定理，三角形面积公式。‎ ‎[解析]∵菱形的对角线互相垂直平分，‎ ‎∴OB＝3，OC＝4，∠BOC＝90°．‎ ‎∴BC＝＝5．‎ ‎∵S△OBC＝OB·OC，又S△OBC＝BC·OE，‎ ‎∴OB·OC＝BC·OE，即3×4＝5OE．‎ ‎∴OE＝．‎ 故答案为：．‎ ‎6. （2016·青海西宁·2分）如图，OP平分∠AOB，∠AOP=15°，PC∥OA，PD⊥OA于点D，PC=4，则PD=　2　．‎ ‎【考点】角平分线的性质；含30度角的直角三角形．‎ ‎【分析】作PE⊥OA于E，根据角平分线的性质可得PE=PD，根据平行线的性质可得∠ACP=∠AOB=30°，由直角三角形中30°的角所对的直角边等于斜边的一半，可求得PE，即可求得PD．‎ ‎【解答】解：作PE⊥OA于E，‎ ‎∵∠AOP=∠BOP，PD⊥OB，PE⊥OA，‎ ‎∴PE=PD（角平分线上的点到角两边的距离相等），‎ ‎∵∠BOP=∠AOP=15°，‎ ‎∴∠AOB=30°，‎ ‎∵PC∥OB，‎ ‎∴∠ACP=∠AOB=30°，‎ ‎∴在Rt△PCE中，PE=PC=×4=2（在直角三角形中，30°角所对的直角边等于斜边的一半），‎ ‎∴PD=PE=2，‎ 故答案是：2．‎ ‎7．（2016·四川宜宾）在平面直角坐标系内，以点P（1，1）为圆心、为半径作圆，则该圆与y轴的交点坐标是　（0，3），（0，﹣1）　．‎ ‎【考点】坐标与图形性质．‎ ‎【分析】在平面直角坐标系中，根据勾股定理先求出直角三角形的另外一个直角边，再根据点P的坐标即可得出答案．‎ ‎【解答】解：以（1，1）为圆心，为半径画圆，与y轴相交，构成直角三角形，‎ 用勾股定理计算得另一直角边的长为2，‎ 则与y轴交点坐标为（0，3）或（0，﹣1）．‎ 故答案为：（0，3），（0，﹣1）．‎ ‎3．（2016·四川内江）如图12所示，已知点C(1，0)，直线y＝－x＋7与两坐标轴分别交于A，B两点，D，E分别是AB，OA上的动点，则△CDE周长的最小值是______．‎ ‎[答案]10‎ ‎[考点]勾股定理，对称问题。‎ ‎[解析]作点C关于y轴的对称点C1(－1，0)，点C关于x轴的对称点C2，连接C1C2交OA于点E，交AB于点D，则此时△CDE的周长最小，且最小值等于C1C2的长．‎ ‎∵OA＝OB＝7，∴CB＝6，∠ABC＝45°．‎ ‎∵AB垂直平分CC2，‎ ‎∴∠CBC2＝90°，C2的坐标为(7，6)．‎ 在△C1BC2中，C1C2＝＝＝10．‎ 即△CDE周长的最小值是10．‎ x y O 答案图 C B A E D C1‎ C2‎ 故答案为：10．‎ ‎8.（2016·湖北黄石·3分）如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是　2π+2　．‎ ‎【分析】如图，用大扇形的面积减去小扇形的面积再加上正方形ABCD的面积．‎ ‎【解答】解：∵OA=AC=2，‎ ‎∴AB=BC=CD=AD=，OC=4，‎ S阴影=+=2π+2，‎ 故答案为：2π+2．‎ ‎【点评】此题考查了扇形的面积公式和旋转的性质以及勾股定理，能够把不规则图形的面积转换为规则图形的面积是解答此题的关键．‎ 一、 解答题 ‎1. （2016·湖北随州·10分）爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AN⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．‎ ‎【特例探究】‎ ‎（1）如图1，当tan∠PAB=1，c=4时，a=　4　，b=　4　；‎ 如图2，当∠PAB=30°，c=2时，a=　　，b=　　；‎ ‎【归纳证明】‎ ‎（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．‎ ‎【拓展证明】‎ ‎（3）如图4，▱ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3，AB=3，求AF的长．‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）①首先证明△APB，△PEF都是等腰直角三角形，求出PA、PB、PE、PF，再利用勾股定理即可解决问题．‎ ‎②连接EF，在RT△PAB，RT△PEF中，利用30°性质求出PA、PB、PE、PF，再利用勾股定理即可解决问题．‎ ‎（2）结论a2+b2=5c2．设MP=x，NP=y，则AP=2x，BP=2y，利用勾股定理分别求出a2、b2、c2即可解决问题．‎ ‎（3）取AB中点H，连接FH并且延长交DA的延长线于P点，首先证明△ABF是中垂三角形，利用（2）中结论列出方程即可解决问题．‎ ‎【解答】（1）解：如图1中，∵CE=AE，CF=BF，‎ ‎∴EF∥AB，EF=AB=2，‎ ‎∵tan∠PAB=1，‎ ‎∴∠PAB=∠PBA=∠PEF=∠PFE=45°，‎ ‎∴PF=PE=2，PB=PA=4，‎ ‎∴AE=BF==2．‎ ‎∴b=AC=2AE=4，a=BC=4．‎ 故答案为4，4．‎ 如图2中，连接EF，‎ ‎，∵CE=AE，CF=BF，‎ ‎∴EF∥AB，EF=AB=1，‎ ‎∵∠PAB=30°，‎ ‎∴PB=1，PA=，‎ 在RT△EFP中，∵∠EFP=∠PAB=30°，‎ ‎∴PE=，PF=，‎ ‎∴AE==，BF==，‎ ‎∴a=BC=2BF=，b=AC=2AE=，‎ 故答案分别为，．‎ ‎（2）结论a2+b2=5c2．‎ 证明：如图3中，连接EF．‎ ‎∵AF、BE是中线，‎ ‎∴EF∥AB，EF=AB，‎ ‎∴△FPE∽△APB，‎ ‎∴==，‎ 设FP=x，EP=y，则AP=2x，BP=2y，‎ ‎∴a2=BC2=4BF2=4（FP2+BP2）=4x2+16y2，‎ b2=AC2=4AE2=4（PE2+AP2）=4y2+16x2，‎ c2=AB2=AP2+BP2=4x2+4y2，‎ ‎∴a2+b2=20x2+20y2=5（4x2+4y2）=5c2．‎ ‎（3）解：如图4中，在△AGE和△FGB中，‎ ‎，‎ ‎∴△AGE≌△FGB，‎ ‎∴BG=FG，取AB中点H，连接FH并且延长交DA的延长线于P点，‎ 同理可证△APH≌△BFH，‎ ‎∴AP=BF，PE=CF=2BF，‎ 即PE∥CF，PE=CF，‎ ‎∴四边形CEPF是平行四边形，‎ ‎∴FP∥CE，‎ ‎∵BE⊥CE，‎ ‎∴FP⊥BE，即FH⊥BG，‎ ‎∴△ABF是中垂三角形，‎ 由（2）可知AB2+AF2=5BF2，‎ ‎∵AB=3，BF=AD=，‎ ‎∴9+AF2=5×（）2，‎ ‎∴AF=4．‎ ‎　‎ ‎2. （2016·四川南充）如图，在Rt△ABC中，∠ACB=90°，∠BAC的平分线交BC于点O，OC=1，以点O为圆心OC为半径作半圆． ‎ ‎（1）求证：AB为⊙O的切线； ‎ ‎（2）如果tan∠CAO=，求cosB的值． ‎ ‎ ‎ ‎【分析】（1）如图作OM⊥AB于M，根据角平分线性质定理，可以证明OM=OC，由此即可证明． ‎ ‎（2）设BM=x，OB=y，列方程组即可解决问题． ‎ ‎【解答】解：（1）如图作OM⊥AB于M， ‎ ‎∵OA平分∠CAB，OC⊥AC，OM⊥AB， ‎ ‎∴OC=OM， ‎ ‎∴AB是⊙O的切线， ‎ ‎（2）设BM=x，OB=y，则y2﹣x2=1 ①， ‎ ‎∵cosB==， ‎ ‎∴=， ‎ ‎∴x2+3x=y2+y ②， ‎ 由①②可以得到：y=3x﹣1， ‎ ‎∴（3x﹣1）2﹣x2=1， ‎ ‎∴x=，y=， ‎ ‎∴cosB==． ‎ ‎ ‎ ‎【点评】本题考查切线的判定、勾股定理、三角函数等知识，解题的关键是记住圆心到直线的距离等于半径，这条直线就是圆的切线，学会设未知数列方程组解决问题，属于中考常考题型． ‎ ‎3．（2016·四川内江）(10分)如图9，在△ABC中，∠ABC＝90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交⊙O于点H，连接BD，FH．‎ ‎(1)试判断BD与⊙O的位置关系，并说明理由；‎ ‎(2)当AB＝BE＝1时，求⊙O的面积；‎ ‎(3)在(2)的条件下，求HG·HB的值．‎ D G H O C E F B A 图9‎ D G H O C E F B A 答案图 ‎[考点]切线的性质与判定定理，三角形的全等，直角三角形斜边上中线定理、勾股定理。‎ ‎(1)直线BD与⊙O相切．理由如下：‎ 如图，连接OB，∵BD是△ABC斜边上的中线，∴DB＝DC．‎ ‎∴∠DBC＝∠C．‎ ‎∵OB＝OE，∴∠OBE＝∠OEB＝∠CED．‎ ‎∵∠C＋∠CED＝90°，‎ ‎∴∠DBC＋∠OBE＝90°．‎ ‎∴BD与⊙O相切； 3分 ‎(2)连接AE．∵AB＝BE＝1，∴AE＝．‎ ‎∵DF垂直平分AC，∴CE＝AE＝．∴BC＝1＋． 4分 ‎∵∠C＋∠CAB＝90°，∠DFA＋∠CAB＝90°，‎ ‎∴∠CAB＝∠DFA．‎ 又∠CBA＝∠FBE＝90°，AB＝BE，‎ ‎∴△CAB≌△FEB．∴BF＝BC＝1＋． 5分 ‎∴EF2＝BE2＋BF2＝12＋(1＋)2＝4＋2． 6分 ‎∴S⊙O＝π·EF2＝π． 7分 ‎(3)∵AB＝BE，∠ABE＝90°，∴∠AEB＝45°．‎ ‎∵EA＝EC，∴∠C＝22.5°． 8分 ‎∴∠H＝∠BEG＝∠CED＝90°－22.5°＝67.5°．‎ ‎∵BH平分∠CBF，∴∠EBG＝∠HBF＝45°．‎ ‎∴∠BGE＝∠BFH＝67.5°．‎ ‎∴BG＝BE＝1，BH＝BF＝1＋． 9分 ‎∴GH＝BH－BG＝．‎ ‎∴HB·HG＝×(1＋)＝2＋． 10分 ‎4.（2016·黑龙江龙东·6分）如图，在平面直角坐标系中，点A、B、C的坐标分别为（﹣1，3）、（﹣4，1）（﹣2，1），先将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是（1，2），再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2，点A1的对应点为点A2．‎ ‎（1）画出△A1B1C1；‎ ‎（2）画出△A2B2C2；‎ ‎（3）求出在这两次变换过程中，点A经过点A1到达A2的路径总长．‎ ‎【考点】作图-旋转变换；作图-平移变换．‎ ‎【分析】（1）由B点坐标和B1的坐标得到△ABC向右平移5个单位，再向上平移1个单位得到△A1B1C1，则根据点平移的规律写出A1和C1的坐标，然后描点即可得到△A1B1C1；‎ ‎（2）利用网格特点和旋转的性质画出点A1的对应点为点A2，点B1的对应点为点B2，点C1的对应点为点C2，从而得到△A2B2C2；‎ ‎（3）先利用勾股定理计算平移的距离，再计算以OA1为半径，圆心角为90°的弧长，然后把它们相加即可得到这两次变换过程中，点A经过点A1到达A2的路径总长．‎ ‎【解答】解：（1）如图，△A1B1C1为所作；‎ ‎（2）如图，△A2B2C2为所作；‎ ‎（3）OA==4，‎ 点A经过点A1到达A2的路径总长=+=+2π．‎ ‎5．（2016·湖北黄石·12分）在△ABC中，AB=AC，∠BAC=2∠DAE=2α．‎ ‎（1）如图1，若点D关于直线AE的对称点为F，求证：△ADF∽△ABC；‎ ‎（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；‎ ‎（3）如图3，若α=45°，点E在BC的延长线上，则等式DE2=BD2+CE2还能成立吗？请说明理由．‎ ‎【分析】（1）根据轴对称的性质可得∠EAF=∠DAE，AD=AF，再求出∠BAC=∠DAF，然后根据两边对应成比例，夹角相等两三角形相似证明；‎ ‎（2）根据轴对称的性质可得EF=DE，AF=AD，再求出∠BAD=∠CAF，然后利用“边角边”证明△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠B，然后求出∠ECF=90°，最后利用勾股定理证明即可；‎ ‎（3）作点D关于AE的对称点F，连接EF、CF，根据轴对称的性质可得EF=DE，AF=AD，再根据同角的余角相等求出∠BAD=∠CAF，然后利用“边角边”证明△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠B，然后求出∠ECF=90°，最后利用勾股定理证明即可．‎ ‎【解答】证明：（1）∵点D关于直线AE的对称点为F，‎ ‎∴∠EAF=∠DAE，AD=AF，‎ 又∵∠BAC=2∠DAE，‎ ‎∴∠BAC=∠DAF，‎ ‎∵AB=AC，‎ ‎∴=，‎ ‎∴△ADF∽△ABC；‎ ‎（2）∵点D关于直线AE的对称点为F，‎ ‎∴EF=DE，AF=AD，‎ ‎∵α=45°，‎ ‎∴∠BAD=90°﹣∠CAD，‎ ‎∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD，‎ ‎∴∠BAD=∠CAF，‎ 在△ABD和△ACF中，，‎ ‎∴△ABD≌△ACF（SAS），‎ ‎∴CF=BD，∠ACF=∠B，‎ ‎∵AB=AC，∠BAC=2α，α=45°，‎ ‎∴△ABC是等腰直角三角形，‎ ‎∴∠B=∠ACB=45°，‎ ‎∴∠ECF=∠ACB+∠ACF=45°+45°=90°，‎ 在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，‎ 所以，DE2=BD2+CE2；‎ ‎（3）DE2=BD2+CE2还能成立．‎ 理由如下：作点D关于AE的对称点F，连接EF、CF，‎ 由轴对称的性质得，EF=DE，AF=AD，‎ ‎∵α=45°，‎ ‎∴∠BAD=90°﹣∠CAD，‎ ‎∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD，‎ ‎∴∠BAD=∠CAF，‎ 在△ABD和△ACF中，，‎ ‎∴△ABD≌△ACF（SAS），‎ ‎∴CF=BD，∠ACF=∠B，‎ ‎∵AB=AC，∠BAC=2α，α=45°，‎ ‎∴△ABC是等腰直角三角形，‎ ‎∴∠B=∠ACB=45°，‎ ‎∴∠ECF=∠ACB+∠ACF=45°+45°=90°，‎ 在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，‎ 所以，DE2=BD2+CE2．‎ ‎【点评】本题是相似形综合题，主要利用了轴对称的性质，相似三角形的判定，同角的余角相等的性质，全等三角形的判定与性质，勾股定理，此类题目，小题间的思路相同是解题的关键．‎ ‎6．（2016·湖北荆州·8分）如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B 时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．‎ ‎【分析】当四边形EDD′F为菱形时，△A′DE是等腰三角形，△A′DE≌△EFC′．先证明CD=DA=DB，得到∠DAC=∠DCA，由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状．由EF∥AB推出∠CEF=∠EA′D，∠EFC=∠A′D′C=∠A′DE，再根据A′D=DE=EF即可证明．‎ ‎【解答】解：当四边形EDD′F为菱形时，△A′DE是等腰三角形，△A′DE≌△EFC′．‎ 理由：∵△BCA是直角三角形，∠ACB=90°，AD=DB，‎ ‎∴CD=DA=DB，‎ ‎∴∠DAC=∠DCA，‎ ‎∵A′C∥AC，‎ ‎∴∠DA′E=∠A，∠DEA′=∠DCA，‎ ‎∴∠DA′E=∠DEA′，‎ ‎∴DA′=DE，‎ ‎∴△A′DE是等腰三角形．‎ ‎∵四边形DEFD′是菱形，‎ ‎∴EF=DE=DA′，EF∥DD′，‎ ‎∴∠CEF=∠DA′E，∠EFC=∠CD′A′，‎ ‎∵CD∥C′D′，‎ ‎∴∠A′DE=∠A′D′C=∠EFC，‎ 在△A′DE和△EFC′中，‎ ‎，‎ ‎∴△A′DE≌△EFC′．‎ ‎【点评】本题考查平移、菱形的性质、全等三角形的判定和性质、直角三角形斜边中线定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．‎ ‎7．（2016·湖北荆州·10分）如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB=15°，连接OF交AB于点E，过点C作OF的平行线交AB的延长线于点D，延长AF交直线CD于点H．‎ ‎（1）求证：CD是半圆O的切线；‎ ‎（2）若DH=6﹣3，求EF和半径OA的长．‎ ‎【分析】（1）连接OB，根据已知条件得到△AOB是等边三角形，得到∠AOB=60°，根据圆周角定理得到∠AOF=∠BOF=30°，根据平行线的性质得到OC⊥CD，由切线的判定定理即可得到结论；‎ ‎（2）根据平行线的性质得到∠DBC=∠EAO=60°，解直角三角形得到BD=BC=AB，推出AE=AD，根据相似三角形的性质得到，求得EF=2﹣，根据直角三角形的性质即可得到结论．‎ ‎【解答】解：（1）连接OB，‎ ‎∵OA=OB=OC，‎ ‎∵四边形OABC是平行四边形，‎ ‎∴AB=OC，‎ ‎∴△AOB是等边三角形，‎ ‎∴∠AOB=60°，‎ ‎∵∠FAD=15°，‎ ‎∴∠BOF=30°，‎ ‎∴∠AOF=∠BOF=30°，‎ ‎∴OF⊥AB，‎ ‎∵CD∥OF，‎ ‎∴CD⊥AD，‎ ‎∵AD∥OC，‎ ‎∴OC⊥CD，‎ ‎∴CD是半圆O的切线；‎ ‎（2）∵BC∥OA，‎ ‎∴∠DBC=∠EAO=60°，‎ ‎∴BD=BC=AB，‎ ‎∴AE=AD，‎ ‎∵EF∥DH，‎ ‎∴△AEF∽△ADH，‎ ‎∴，‎ ‎∵DH=6﹣3，‎ ‎∴EF=2﹣，‎ ‎∵OF=OA，‎ ‎∴OE=OA﹣（2﹣），‎ ‎∵∠AOE=30°，‎ ‎∴==，‎ 解得：OA=2．‎ ‎【点评】本题考查了切线的判定，平行四边形的性质，直角三角形的性质，等边三角形的判定和性质，连接OB构造等边三角形是解题的关键．‎ ‎8.（2016·福建龙岩·12分）图1是某公交公司1路车从起点站A站途经B站和C站，最终到达终点站D站的格点站路线图．（8×8的格点图是由边长为1的小正方形组成）‎ ‎（1）求1路车从A站到D站所走的路程（精确到0.1）；‎ ‎（2）在图2、图3和图4的网格中各画出一种从A站到D站的路线图．（要求：①与图1路线不同、路程相同；②途中必须经过两个格点站；③所画路线图不重复）‎ ‎【考点】作图—应用与设计作图；勾股定理的应用．‎ ‎【分析】（1）先根据网格求得AB、BC、CD三条线段的长，再相加求得所走的路程的近似值；‎ ‎（2）根据轴对称、平移或中心对称等图形的变换进行作图即可．‎ ‎【解答】解：（1）根据图1可得：，，CD=3‎ ‎∴A站到B站的路程=≈9.7；‎ ‎（2）从A站到D站的路线图如下：‎ ‎9．（2016·山东省菏泽市·3分）如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．‎ ‎（1）求证：四边形DEFG是平行四边形；‎ ‎（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．‎ ‎【考点】平行四边形的判定与性质．‎ ‎【分析】（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；‎ ‎（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．‎ ‎【解答】解：（1）∵D、G分别是AB、AC的中点，‎ ‎∴DG∥BC，DG=BC，‎ ‎∵E、F分别是OB、OC的中点，‎ ‎∴EF∥BC，EF=BC，‎ ‎∴DE=EF，DG∥EF，‎ ‎∴四边形DEFG是平行四边形；‎ ‎（2）∵∠OBC和∠OCB互余，‎ ‎∴∠OBC+∠OCB=90°，‎ ‎∴∠BOC=90°，‎ ‎∵M为EF的中点，OM=3，‎ ‎∴EF=2OM=6．‎ 由（1）有四边形DEFG是平行四边形，‎ ‎∴DG=EF=6．‎ ‎【点评】此题是平行四边形的判定与性质题，主要考查了平行四边形的判定和性质，三角形的中位线，直角三角形的性质，解本题的关键是判定四边形DEFG是平行四边形．‎