2010年辽宁省锦州市中考数学试题 7页

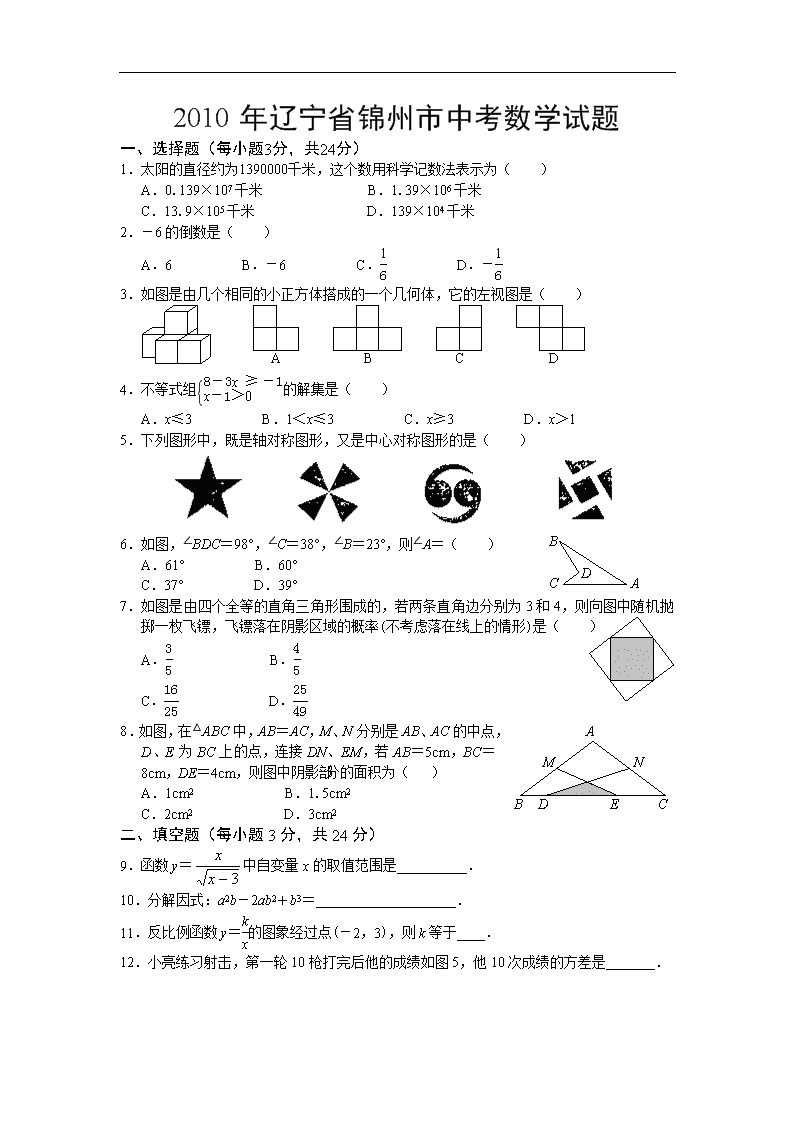
‎2010年辽宁省锦州市中考数学试题 一、选择题（每小题3分，共24分）‎ ‎1．太阳的直径约为1390000千米，这个数用科学记数法表示为（ ）‎ A．0.139×107千米 B．1.39×106千米 C．13.9×105千米 D．139×104千米 ‎2．－6的倒数是（ ）‎ A．6 B．－‎6 C． D．－ ‎3．如图是由几个相同的小正方体搭成的一个几何体，它的左视图是（ ）‎ A B C D ‎4．不等式组的解集是（ ）‎ A．x≤3 B．1＜x≤‎3 C．x≥3 D．x＞1‎ ‎5．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）‎ ‎6．如图，∠BDC＝98°，∠C＝38°，∠B＝23°，则∠A＝（ ）‎A B C D A．61° B．60°‎ C．37° D．39°‎ ‎7．如图是由四个全等的直角三角形围成的，若两条直角边分别为3和4，则向图中随机抛掷一枚飞镖，飞镖落在阴影区域的概率(不考虑落在线上的情形)是（ ）‎ A． B． C． D． B C M N A D E ‎8．如图，在△ABC中，AB＝AC，M、N分别是AB、AC的中点，D、E为BC上的点，连接DN、EM，若AB＝‎5cm，BC＝‎8cm，DE＝‎4cm，则图中阴影部分的面积为（ ）‎ A．‎1cm2 B．‎1.5cm2‎ C．‎2cm2 D．‎3cm2‎ 二、填空题（每小题3分，共24分）‎ ‎9．函数y＝中自变量x的取值范围是__________．‎ ‎10．分解因式：a2b－2ab2＋b3＝____________________．‎ ‎11．反比例函数y＝的图象经过点(－2，3)，则k等于____．‎ ‎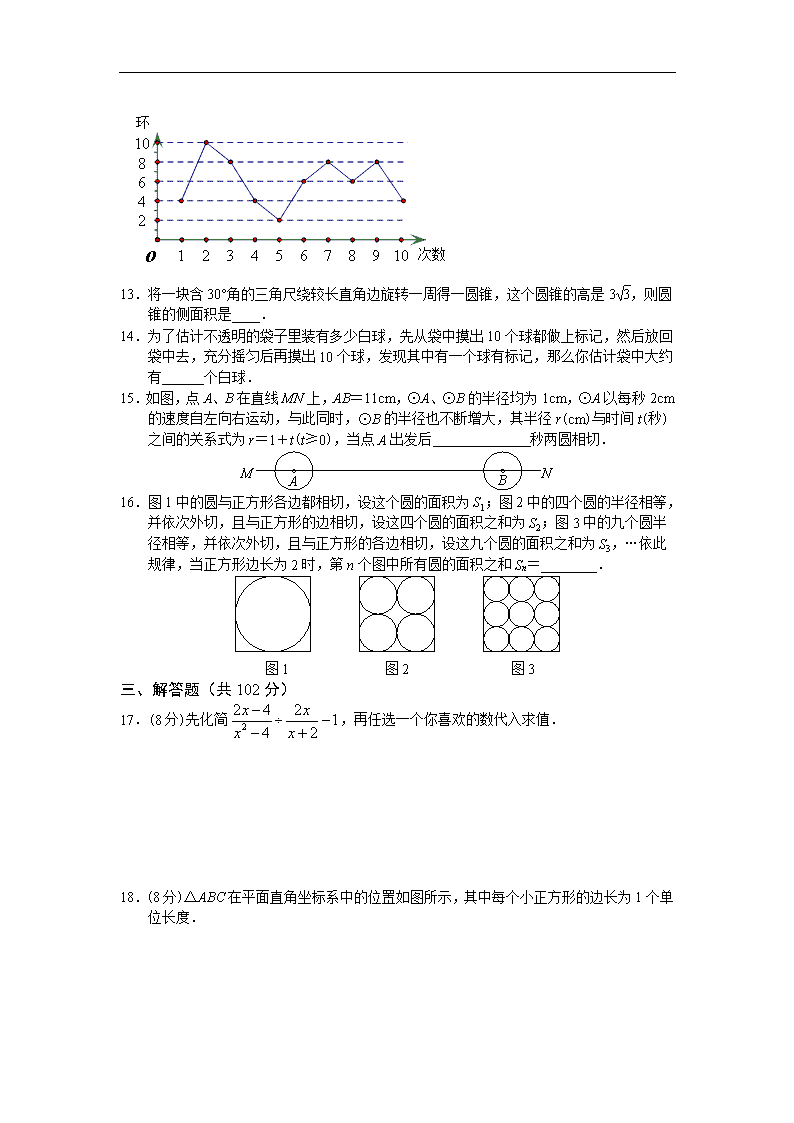12．小亮练习射击，第一轮10枪打完后他的成绩如图5，他10次成绩的方差是_______．‎ ‎13．将一块含30°角的三角尺绕较长直角边旋转一周得一圆锥，这个圆锥的高是3，则圆锥的侧面积是____．‎ ‎14．为了估计不透明的袋子里装有多少白球，先从袋中摸出10个球都做上标记，然后放回袋中去，充分摇匀后再摸出10个球，发现其中有一个球有标记，那么你估计袋中大约有______个白球．‎ ‎15．如图，点A、B在直线MN上，AB＝‎11cm，⊙A、⊙B的半径均为‎1cm，⊙A以每秒‎2cm的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r(cm)与时间t(秒)之间的关系式为r＝1＋t(t≥0)，当点A出发后 秒两圆相切．‎ B A M N ‎16．图1中的圆与正方形各边都相切，设这个圆的面积为S1；图2中的四个圆的半径相等，并依次外切，且与正方形的边相切，设这四个圆的面积之和为S2；图3中的九个圆半径相等，并依次外切，且与正方形的各边相切，设这九个圆的面积之和为S3，…依此规律，当正方形边长为2时，第n个图中所有圆的面积之和Sn＝________．‎ 图1‎ 图2‎ 图3‎ 三、解答题（共102分）‎ ‎17．(8分)先化简，再任选一个你喜欢的数代入求值．‎ ‎18．(8分)△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．‎ ‎(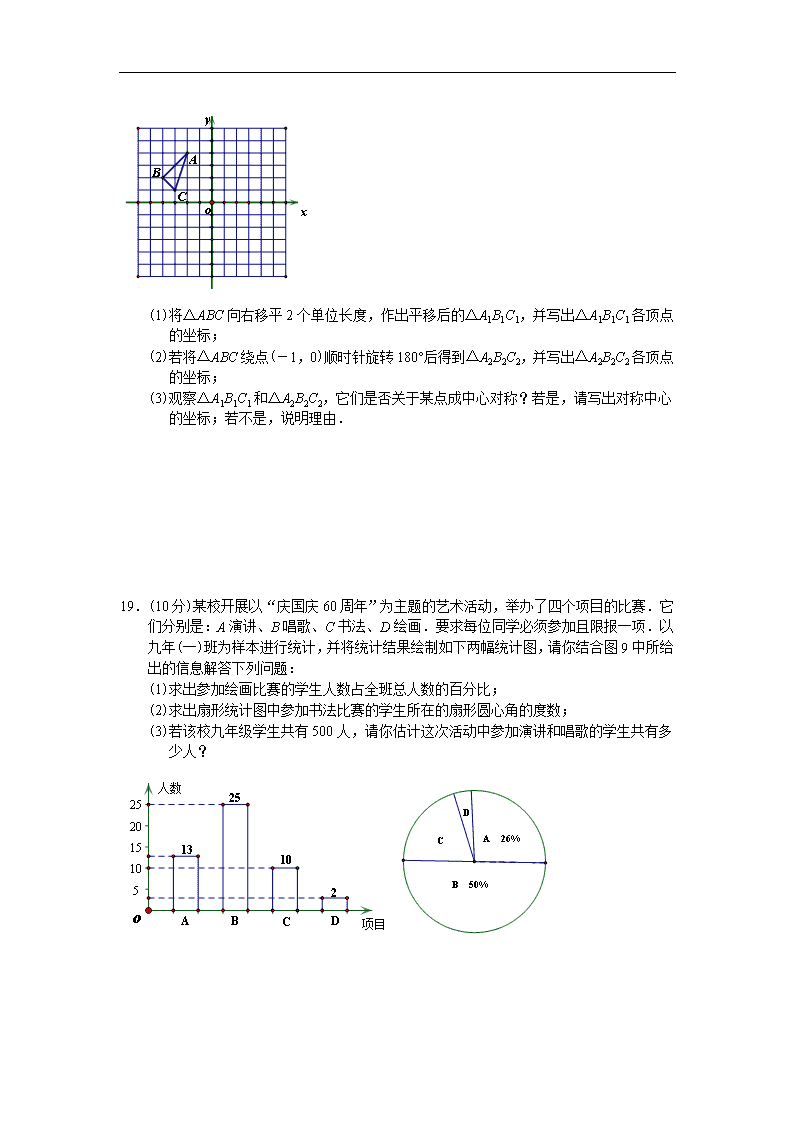1)将△ABC向右移平2个单位长度，作出平移后的△A1B‎1C1，并写出△A1B‎1C1各顶点的坐标；‎ ‎(2)若将△ABC绕点(－1，0)顺时针旋转180°后得到△A2B‎2C2，并写出△A2B‎2C2各顶点的坐标；‎ ‎(3)观察△A1B‎1C1和△A2B‎2C2，它们是否关于某点成中心对称？若是，请写出对称中心的坐标；若不是，说明理由．‎ ‎19．(10分)某校开展以“庆国庆60周年”为主题的艺术活动，举办了四个项目的比赛．它们分别是：A演讲、B唱歌、C书法、D绘画．要求每位同学必须参加且限报一项．以九年(一)班为样本进行统计，并将统计结果绘制如下两幅统计图，请你结合图9中所给出的信息解答下列问题：‎ ‎(1)求出参加绘画比赛的学生人数占全班总人数的百分比；‎ ‎(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数；‎ ‎(3)若该校九年级学生共有500人，请你估计这次活动中参加演讲和唱歌的学生共有多少人？‎ ‎20．(10分)为了加快城市经济发展，某市准备修建一座横跨南北的大桥．如图10所示，测量队在点A处观测河对岸水边有一点C，测得C在北偏东60°的方向上，沿河岸向东前行‎30米到达B处，测得C在北偏东45°的方向上，请你根据以上数据帮助该测量队计算出这条河的宽度(结果保留根号)．‎ ‎21．(10分)小刚和小明玩“石头”、“剪子”、“布”的游戏，游戏的规则为：“石头”胜“剪子”，“剪子”胜“布”，“布”胜“石头”，若两人所出手势相同，则为平局．‎ ‎(1)玩一次小刚出“石头”的概率是多少？‎ ‎(2)玩一次小刚胜小明的概率是多少？请加以说明．‎ ‎22．(10分)根据规划设计，某市工程队准备在开发区修建一条长‎300米的盲道．铺设了‎60米后，由于采用新的施工方式，实际每天修建盲道的长度比原计划增加‎10米，结果共用了8天完成任务，该工程队改进技术后每天铺设盲道多少米？‎ B A O D F C E ‎1‎ ‎2‎ ‎23．(10分)如图，AB为⊙O的直径，AD平分∠BAC交⊙O于点D，DE⊥AC交AC的延长线于点E，FB是⊙O的切线交AD的延长线于点F．‎ ‎(1)求证：DE是⊙O的切线；‎ ‎(2)若DE＝3，⊙O的半径为5，求BF的长．‎ ‎24．(10分)某商场购进一批单价为50元的商品，规定销售时单价不低于进价，每件的利润不超过40%．其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一次函数．‎ ‎(1)求y与x之间的函数关系式，并求出x的取值范围；‎ ‎(2)设该公司获得的总利润(总利润＝总销售额－总成本)为w元，求w与x之间的函数关系式．当销售单价为何值时，所获利润最大？最大利润是多少？‎ O ‎400‎ ‎300‎ ‎60‎ ‎70‎ y/件 x/元 ‎25．(12分)如图，直角梯形ABCD和正方形EFGC的边BC、CG在同一条直线上，AD∥BC，AB⊥BC于点B，AD＝4，AB＝6，BC＝8，直角梯形ABCD的面积与正方形EFGC的面积相等，将直角梯形ABCD沿BG向右平行移动，当点C与点G重合时停止移动．设梯形与正方形重叠部分的面积为S．‎ ‎(1)求正方形的边长；‎ ‎(2)设直角梯形ABCD的顶点C向右移动的距离为x，求S与x的函数关系式；‎ A B C G F E D ‎(3)当直角梯形ABCD向右移动时，它与正方形EFGC的重叠部分面积S，能否等于直角梯形ABCD面积的一半？若能，请求出此时运动的距离x的值；若不能，请说明理由．‎ ‎26．(14分)如图，抛物线与x轴交于A(x1，0)、B(x2，0)两点，且x1＞x2，与y轴交于点C(0，4)，其中x1、x2是方程x2－2x－8＝0的两个根．‎ ‎(1)求这条抛物线的解析式；‎ ‎(2)点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；‎ ‎(3)探究：若点Q是抛物线对称轴上的点，是否存在这样的点Q，使△QBC成为等腰三 A P O B E C x y 角形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．‎