中考动态问题教学设计 4页

‎《中考动态问题》教学设计 一、教材分析 ‎1．教学内容、地位与作用 本节课的内容是人教版教材中考专题复习动态问题，可以涉及三角形、四边形、相似、圆、解直角三角形、函数、方程等重点内容，是中考的重要题型，也是培养与考查学生解决问题与探究能力的重要手段与途径．‎ ‎2．教学目标 根据本节课的实际内容与新课标的相关要求，制定教学目标如下：‎ 知识与技能：（1）会灵活运用相关知识解决动点、动线与动图问题．‎ ‎（2）经历图形的抽象、分类、运动、位置确定等过程，掌握图形与几何的知识基础和基本技能．‎ 过程与方法：（1）通过探究各类动态问题的过程，形成利用数形结合与分类讨论等思想处理问题的习惯．‎ ‎（2）获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识．‎ 情感、态度与价值观：（1）积极参与数学活动，养成合作交流，反思质疑等学习习惯.‎ ‎（2）体验获得成功的乐趣，锻炼克服困难的意志，建立自信心．‎ ‎3．教学重点、难点与关键 本节课的学习重点是探索并掌握中考动态问题的解法策略；难点是知识的综合运用与想象力的培养．在具体学习过程中，通过观察、操作、想象、推理、交流等学习活动，引导学生积极思考，通过几何画板的动态演示，形成形象思维并在静态图中解决问题是突破重、难点的关键． ‎ 二、学情分析 学生通过初中数学教材的学习，对各知识点已有基本的认识与初步的运用，这也是综合运用知识解决问题的必要基础，但在动态问题中知识的综合应用比较生疏，因此，在具体学习中可能会产生一定的困难．故而在教学中应以简单明白，深入浅出的分析，直观、形象的演示与操作，引发学生的兴趣，感悟知识的形成与发展过程，充分发挥学生学习的主动性．‎ 三、教法与学法 教法：在设置探究活动中，突出启发式、讨论法、讲练结合、多媒体课件演示等方式进行教学；‎ 学法：动手操作、自主探索与小组合作交流相结合．‎ ‎ 四、教学流程设计 ‎（一）明确目标 多媒体出示学习目标，让学生感知，明晰学习任务．同时教师简单阐述动态问题的基本特点，让学生初步认识该类问题．‎ ‎（二）问题探究 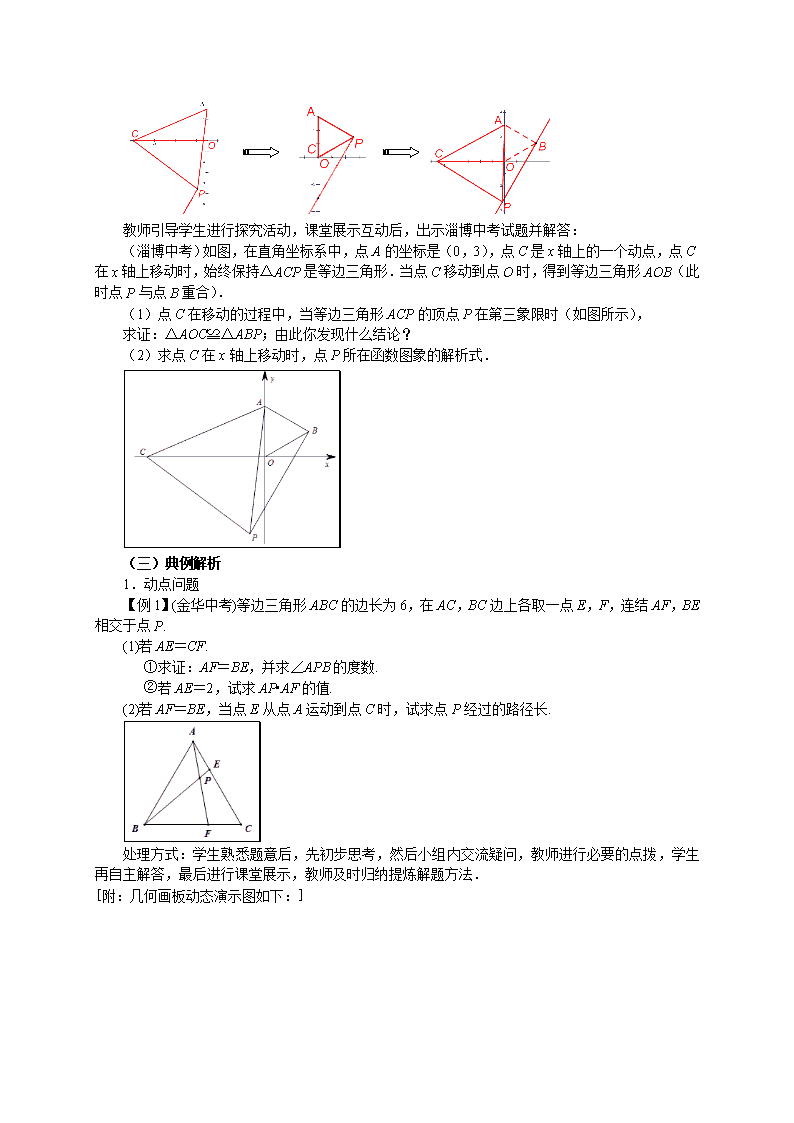活动 观察(教师进行几何画板动态演示)：在平面直角坐标系中，点A是y轴正半轴上一定点，点C是x轴上一点，以AC为边作等边三角形ACP，则点C在右运动中，点P是如何进行运动的？你发现了什么？为什么？当点C运动到点O时点P在哪个象限？由此情景你能编拟一道数学问题吗？‎ ‎ ‎ 教师引导学生进行探究活动，课堂展示互动后，出示淄博中考试题并解答：‎ ‎（淄博中考）如图，在直角坐标系中，点A的坐标是（0，3），点C是x轴上的一个动点，点C在x轴上移动时，始终保持△ACP是等边三角形．当点C移动到点O时，得到等边三角形AOB（此时点P与点B重合）．‎ ‎（1）点C在移动的过程中，当等边三角形ACP的顶点P在第三象限时（如图所示），‎ 求证：△AOC≌△ABP；由此你发现什么结论？‎ ‎（2）求点C在x轴上移动时，点P所在函数图象的解析式． ‎ ‎（三）典例解析 ‎1．动点问题 ‎【例1】(金华中考)等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连结AF，BE相交于点P. ‎ ‎(1)若AE＝CF.‎ ‎ ①求证：AF＝BE，并求∠APB的度数.‎ ‎ ②若AE＝2，试求AP•AF的值.‎ ‎(2)若AF＝BE，当点E从点A运动到点C时，试求点P经过的路径长. 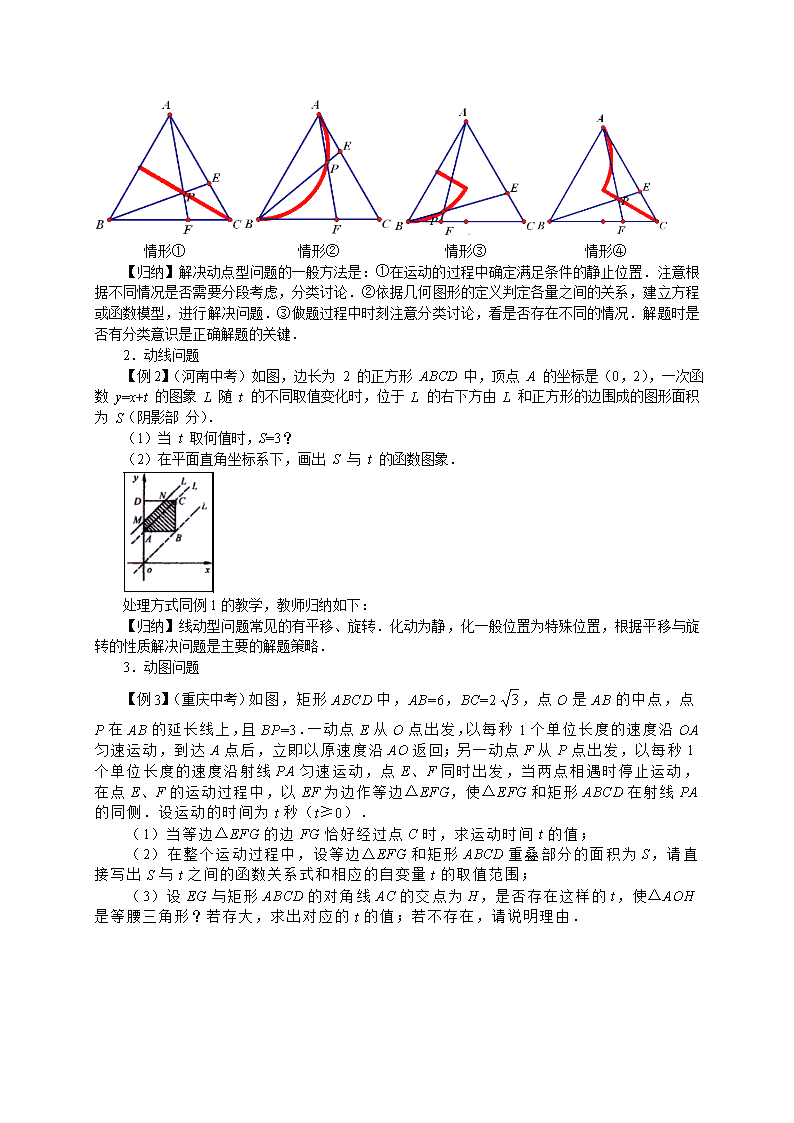‎ 处理方式：学生熟悉题意后，先初步思考，然后小组内交流疑问，教师进行必要的点拨，学生再自主解答，最后进行课堂展示，教师及时归纳提炼解题方法．‎ ‎[附：几何画板动态演示图如下：]‎ 情形① 情形② 情形③ 情形④‎ ‎【归纳】解决动点型问题的一般方法是：①在运动的过程中确定满足条件的静止位置．注意根据不同情况是否需要分段考虑，分类讨论．②依据几何图形的定义判定各量之间的关系，建立方程或函数模型，进行解决问题．③做题过程中时刻注意分类讨论，看是否存在不同的情况．解题时是否有分类意识是正确解题的关键．‎ ‎2．动线问题 ‎【例2】（河南中考）如图，边长为 2 的正方形 ABCD 中，顶点 A 的坐标是（0，2），一次函数 y=x+t 的图象 L 随 t 的不同取值变化时，位于 L 的右下方由 L 和正方形的边围成的图形面积为 S（阴影部 分）． ‎ ‎（1）当 t 取何值时，S=3？ ‎ ‎（2）在平面直角坐标系下，画出 S 与 t 的函数图象． ‎ 处理方式同例1的教学，教师归纳如下：‎ ‎【归纳】线动型问题常见的有平移、旋转．化动为静，化一般位置为特殊位置，根据平移与旋转的性质解决问题是主要的解题策略．‎ ‎3．动图问题 ‎【例3】（重庆中考）如图，矩形ABCD中，AB=6，BC=2，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．‎ ‎（1）当等边△EFG的边FG恰好经过点C时，求运动时间t的值；‎ ‎（2）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；‎ ‎（3）设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存大，求出对应的t的值；若不存在，请说明理由．‎ 方式同例1、2的教学，教师归纳如下：‎ ‎【归纳】动面型问题一方面是指某个图形(三角形或四边形)绕着某个点旋转或沿某直线平移，另一方面是指图形由特殊图形变为一般图形．‎ ‎（四）课堂总结：‎ ‎1．中考动态有哪些常见类型？‎ ‎2．解决动态问题的一般思路是什么？‎ ‎3．本节课你还有哪些收获与困惑与大家交流？‎ ‎（五）达标拓展 ‎1．（玉林中考）如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止，设小三角形移动的距离为x，两个三角形重叠面积为y，则y关于x的函数图象是（ ）‎ ‎ ‎ A． B． C． D．‎