威海市2015年中考数学卷 19页

山东省威海市2015年中考数学试卷 一、选择题 ‎1．检验4个工件，其中超过标准质量的克数记作正数，不足标准质量的克数记作负数．从轻重的角度看，最接近标准的工件是（　　）‎ ‎　‎ A．‎ ‎﹣2‎ B．‎ ‎﹣3‎ C．‎ ‎3‎ D．‎ ‎5‎ 考点：‎ 正数和负数．.‎ 分析：‎ 根据正负数的意义，绝对值最小的即为最接近标准的．‎ 解答：‎ 解：|﹣2|=2，|﹣3|=3，|3|=3，|5|=5，‎ ‎∵2＜3＜5，‎ ‎∴从轻重的角度来看，最接近标准的是记录为﹣2．‎ 故选A．‎ 点评：‎ 此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．‎ ‎　‎ ‎2．（3分）（2015•威海）如图，在△ABC中，∠ACB=90°，∠ABC=26°，BC=5．若用科学计算器求边AC的长，则下列按键顺序正确的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 计算器—三角函数．.‎ 分析：‎ 根据正切函数的定义，可得tan∠B=，根据计算器的应用，可得答案．‎ 解答：‎ 接：由tan∠B=，得 AC=BC•tanB=5×tan26．‎ 故选：D．‎ 点评：‎ 本题考查了计算器，利用了锐角三角函数，计算器的应用，熟练应用计算器是解题关键．‎ ‎　‎ ‎3．（3分）（2015•威海）据中国新闻网报道，在‎2014年11月17日公布的全球超级计算机500强榜单中，中国国防科技大学研制的“天河”二号超级计算机，以峰值计算速度每秒5.49亿亿次、持续计算速度每秒3.39亿亿次双精度浮点运算的优异性能位居榜首，第四次摘得全球运行速度最快的超级计算机桂冠．用科学记数法表示“5.49亿亿”，记作（　　）‎ ‎　‎ A．‎ ‎5.49×1018‎ B．‎ ‎5.49×1016‎ C．‎ ‎5.49×1015‎ D．‎ ‎5.49×1014‎ 考点：‎ 科学记数法—表示较大的数．.‎ 分析：‎ 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ 解答：‎ 解：将5.49亿亿用科学记数法表示为5.49×1016．‎ 故选B．‎ 点评：‎ 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎　‎ ‎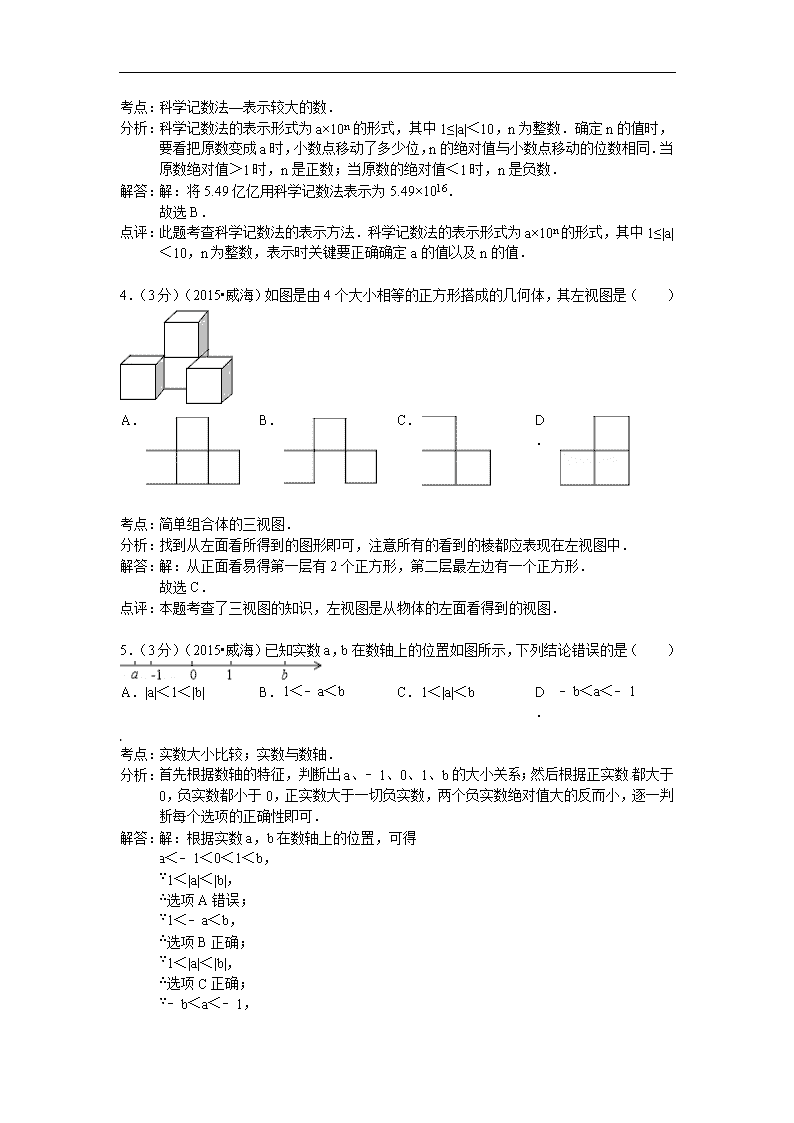4．（3分）（2015•威海）如图是由4个大小相等的正方形搭成的几何体，其左视图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 简单组合体的三视图．.‎ 分析：‎ 找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在左视图中．‎ 解答：‎ 解：从正面看易得第一层有2个正方形，第二层最左边有一个正方形．‎ 故选C．‎ 点评：‎ 本题考查了三视图的知识，左视图是从物体的左面看得到的视图．‎ ‎　‎ ‎5．（3分）（2015•威海）已知实数a，b在数轴上的位置如图所示，下列结论错误的是（　　）‎ ‎　‎ A．‎ ‎|a|＜1＜|b|‎ B．‎ ‎1＜﹣a＜b C．‎ ‎1＜|a|＜b D．‎ ‎﹣b＜a＜﹣1‎ 考点：‎ 实数大小比较；实数与数轴．.‎ 分析：‎ 首先根据数轴的特征，判断出a、﹣1、0、1、b的大小关系；然后根据正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，逐一判断每个选项的正确性即可．‎ 解答：‎ 解：根据实数a，b在数轴上的位置，可得 a＜﹣1＜0＜1＜b，‎ ‎∵1＜|a|＜|b|，‎ ‎∴选项A错误；‎ ‎∵1＜﹣a＜b，‎ ‎∴选项B正确；‎ ‎∵1＜|a|＜|b|，‎ ‎∴选项C正确；‎ ‎∵﹣b＜a＜﹣1，‎ ‎∴选项D正确．‎ 故选：A．‎ 点评：‎ ‎（1）此题主要考查了实数与数轴，要熟练掌握，解答此题的关键是要明确：实数与数轴上的点是一一对应关系．任意一个实数都可以用数轴上的点表示；反之，数轴上的任意一个点都表示一个实数．数轴上的任一点表示的数，不是有理数，就是无理数．‎ ‎（2）此题还考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．‎ ‎　‎ ‎6．（3分）（2015•威海）若点A（a+1，b﹣2）在第二象限，则点B（﹣a，b+1）在（　　）‎ ‎　‎ A．‎ 第一象限 B．‎ 第二象限 C．‎ 第三象限 D．‎ 第四象限 考点：‎ 点的坐标．.‎ 分析：‎ 根据第二象限内的点的横坐标小于零，纵坐标大于零，可得关于a、b的不等式，再根据不等式的性质，可得B点的坐标符号．‎ 解答：‎ 解：由A（a+1，b﹣2）在第二象限，得 a+1＜0，b﹣2＞0．‎ 解得a＜﹣1，b＞2．‎ 由不等式的性质，得 ‎﹣a＞1，b+1＞3，‎ 点B（﹣a，b+1）在第一象限，‎ 故选：A．‎ 点评：‎ 本题考查了点的坐标，利用第二象限内点的横坐标小于零，纵坐标大于零得出不等式，又利用不等式的性质得出B点的坐标符号是解题关键．‎ ‎　‎ ‎7．（3分）（2015•威海）下列运算正确的是（　　）‎ ‎　‎ A．‎ ‎（﹣3mn）2=﹣6m2n2‎ B．‎ ‎4x4+2x4+x4=6x4‎ ‎　‎ C．‎ ‎（xy）2÷（﹣xy）=﹣xy D．‎ ‎（a﹣b）（﹣a﹣b）=a2﹣b2‎ 考点：‎ 整式的除法；合并同类项；幂的乘方与积的乘方；平方差公式．.‎ 分析：‎ 根据积的乘方、合并同类项、整式的乘法、除法，即可解答．‎ 解答：‎ 解：A、（﹣3mn）2=9m2n2，故错误；‎ B、4x4+2x4+x4=7x4，故错误；‎ C、正确；‎ D、（a﹣b）（﹣a﹣b）=﹣（a2﹣b2）=b2﹣a2，故错误；‎ 故选：C．‎ 点评：‎ 本题考查了积的乘方、合并同类项、整式的乘法、除法，解决本题的关键是熟记相关法则．‎ ‎　‎ ‎8．（3分）（2015•威海）若用一张直径为20cm的半圆形铁片做一个圆锥的侧面，接缝忽略不计，则所得圆锥的高为（　　）‎ ‎　‎ A．‎ ‎5cm B．‎ ‎5cm C．‎ cm D．‎ ‎10cm 考点：‎ 圆锥的计算．.‎ 专题：‎ 计算题．‎ 分析：‎ 设这个圆锥的底面半径为r，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=，解得r=5，然后利用勾股定理计算这个圆锥的高．‎ 解答：‎ 解：设这个圆锥的底面半径为r，‎ 根据题意得2πr=，解得r=5，‎ 所以这个圆锥的高==5（cm）．‎ 故选A．‎ 点评：‎ 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．‎ ‎　‎ ‎9．（3分）（2015•威海）如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为（　　）‎ ‎　‎ A．‎ ‎68°‎ B．‎ ‎88°‎ C．‎ ‎90°‎ D．‎ ‎112°‎ 考点：‎ 圆周角定理．.‎ 分析：‎ 如图，作辅助圆；首先运用圆周角定理证明∠CAD=2∠CBD，∠BAC=2∠BDC，结合已知条件∠CBD=2∠BDC，得到∠CAD=2∠BAC，即可解决问题．‎ 解答：‎ 解：如图，∵AB=AC=AD，‎ ‎∴点B、C、D在以点A为圆心，‎ 以AB的长为半径的圆上；‎ ‎∵∠CBD=2∠BDC，‎ ‎∠CAD=2∠CBD，∠BAC=2∠BDC，‎ ‎∴∠CAD=2∠BAC，而∠BAC=44°，‎ ‎∴∠CAD=88°，‎ 故选B．‎ 点评：‎ 该题主要考查了圆周角定理及其推论等几何知识点及其应用问题；解题的方法是作辅助圆，将分散的条件集中；解题的关键是灵活运用圆周角定理及其推论等几何知识点来分析、判断、推理或解答．‎ ‎　‎ ‎10．（3分）（2015•威海）甲、乙两布袋装有红、白两种小球，两袋装球总数量相同，两种小球仅颜色不同．甲袋中，红球个数是白球个数的2倍；乙袋中，红球个数是白球个数的3倍，将乙袋中的球全部倒入甲袋，随机从甲袋中摸出一个球，摸出红球的概率是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 概率公式．.‎ 分析：‎ 首先根据每个袋子中球的倍数设出每个袋子中球的个数，然后利用概率公式求解即可．‎ 解答：‎ 解：∵甲袋中，红球个数是白球个数的2倍，‎ ‎∴设白球为4x，则红球为8x，‎ ‎∴两种球共有12x个，‎ ‎∵乙袋中，红球个数是白球个数的3倍，且两袋中球的数量相同，‎ ‎∴红球为9x，白球为3x，‎ ‎∴混合后摸出红球的概率为：=，‎ 故选C．‎ 点评：‎ 此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．‎ ‎　‎ ‎11．（3分）（2015•威海）如图，已知△ABC为等边三角形，AB=2，点D为边AB上一点，过点D作DE∥AC，交BC于E点；过E点作EF⊥DE，交AB的延长线于F点．设AD=x，△DEF的面积为y，则能大致反映y与x函数关系的图象是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 动点问题的函数图象．.‎ 分析：‎ 根据平行线的性质可得∠EDC=∠B=60°，根据三角形内角和定理即可求得∠F=30°，然后证得△EDC是等边三角形，从而求得ED=DC=2﹣x，再根据直角三角形的性质求得EF，最后根据三角形的面积公式求得y与x函数关系式，根据函数关系式即可判定．‎ 解答：‎ 解：∵△ABC是等边三角形，‎ ‎∴∠B=60°，‎ ‎∵DE∥AB，‎ ‎∴∠EDC=∠B=60°，‎ ‎∵EF⊥DE，‎ ‎∴∠DEF=90°，‎ ‎∴∠F=90°﹣∠EDC=30°；‎ ‎∵∠ACB=60°，∠EDC=60°，‎ ‎∴△EDC是等边三角形．‎ ‎∴ED=DC=2﹣x，‎ ‎∵∠DEF=90°，∠F=30°，‎ ‎∴EF=ED=（2﹣x）．‎ ‎∴y=ED•EF=（2﹣x）•（2﹣x），‎ 即y=（x﹣2）2，（x＜2），‎ 故选A．‎ 点评：‎ 本题考查了等边三角形的判定与性质，以及直角三角形的性质，特殊角的三角函数、三角形的面积等．‎ ‎　‎ ‎12．（3分）（2015•威海）如图，正六边形A1B1C1D1E1F1的边长为2，正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切，正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切，…按这样的规律进行下去，A10B10C10D10E10F10的边长为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 正多边形和圆．.‎ 专题：‎ 规律型．‎ 分析：‎ 连结OE1，OD1，OD2，如图，根据正六边形的性质得∠E1OD1=60°，则△E1OD1‎ 为等边三角形，再根据切线的性质得OD2⊥E1D1，于是可得OD2=E1D1=×2，利用正六边形的边长等于它的半径得到正六边形A2B2C2D2E2F2的边长=×2，同理可得正六边形A3B3C3D3E3F3的边长=（）2×2，依此规律可得正六边形A10B10C10D10E10F10的边长=（）9×2，然后化简即可．‎ 解答：‎ 解：连结OE1，OD1，OD2，如图，‎ ‎∵六边形A1B1C1D1E1F1为正六边形，‎ ‎∴∠E1OD1=60°，‎ ‎∴△E1OD1为等边三角形，‎ ‎∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切，‎ ‎∴OD2⊥E1D1，‎ ‎∴OD2=E1D1=×2，‎ ‎∴正六边形A2B2C2D2E2F2的边长=×2，‎ 同理可得正六边形A3B3C3D3E3F3的边长=（）2×2，‎ 则正六边形A10B10C10D10E10F10的边长=（）9×2=．‎ 故选D．‎ 点评：‎ 本题考查了正多边形与圆的关系：把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆．记住正六边形的边长等于它的半径．‎ ‎　‎ 二、填空题 ‎13．（3分）（2015•威海）计算：20+（）﹣1的值为　3　．‎ 考点：‎ 负整数指数幂；零指数幂．.‎ 分析：‎ 根据0次幂和负整数指数幂，即可解答．‎ 解答：‎ 解：20+（）﹣1‎ ‎=1+2‎ ‎=3．‎ 故答案为：3．‎ 点评：‎ 本题考查了0次幂和负整数指数幂，解决本题的关键是熟记相关法则．‎ ‎　‎ ‎14．（3分）（2015•威海）如图，直线a∥b，∠1=110°，∠2=55°，则∠3的度数为　55°　．‎ 考点：‎ 平行线的性质．.‎ 分析：‎ 要求∠3的度数，结合图形和已知条件，先求由两条平行线所构成的同位角或内错角，再利用三角形的外角的性质就可求解．‎ 解答：‎ 解：如图：‎ ‎∵∠2=∠5=55°，‎ 又∵a∥b，‎ ‎∴∠1=∠4=100°．‎ ‎∵∠4=∠3+∠5，‎ ‎∴∠3=110°﹣55°=55°，‎ 故答案为：55°．‎ 点评：‎ 本题考查了三角形的外角的性质和平行线的性质；三角形的外角的性质：三角形的外角等于和它不相邻的两个内角的和；平行线的性质：两直线平行，同位角相等．‎ ‎　‎ ‎15．（3分）（2015•威海）因式分解：﹣2x2y+12xy﹣18y=　﹣2y（x﹣3）2　．‎ 考点：‎ 提公因式法与公式法的综合运用．.‎ 专题：‎ 计算题．‎ 分析：‎ 原式提取公因式，再利用完全平方公式分解即可．‎ 解答：‎ 解：原式=﹣2y（x2﹣6x+9）‎ ‎=﹣2y（x﹣3）2．‎ 故答案为：﹣2y（x﹣3）2．‎ 点评：‎ 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．‎ ‎　‎ ‎16．（3分）（2015•威海）分式方程的解为　x=4　．‎ 考点：‎ 解分式方程．.‎ 专题：‎ 计算题．‎ 分析：‎ 原式变形后，去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ 解答：‎ 解：去分母得：1﹣x=﹣1﹣2x+6，‎ 解得：x=4，‎ 经检验x=4是分式方程的解．‎ 点评：‎ 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．‎ ‎　‎ ‎17．（3分）（2015•威海）如图，点A、B的坐标分别为（0，2），（3，4），点P为x轴上的一点，若点B关于直线AP的对称点B′恰好落在x轴上，则点P的坐标为　（）　．‎ 考点：‎ 一次函数综合题．.‎ 分析：‎ 先用待定系数法求出直线AB的解析式，由对称的性质得出AP⊥AB，求出直线AP的解析式，然后求出直线AP与x轴的交点即可．‎ 解答：‎ 解：设直线AB的解析式为：y=kx+b，‎ 把A（0，2），B（3，4）代入得：，‎ 解得：k=，b=2，‎ ‎∴直线AB的解析式为：y=x+2；‎ ‎∵点B与B′关于直线AP对称，‎ ‎∴AP⊥AB，∴设直线AP的解析式为：y=﹣x+c，‎ 把点A（0，2）代入得：c=2，‎ ‎∴直线AP的解析式为：y=﹣x+2，‎ 当y=0时，﹣x+2=0，‎ 解得：x=，‎ ‎∴点P的坐标为：（）；‎ 故答案为：（）．‎ 点评：‎ 本题是一次函数综合题目，考查了用待定系数法确定一次函数的解析式、轴对称的性质、垂线的关系等知识；本题有一定难度，综合性强，由直线AB的解析式进一步求出直线AP的解析式是解决问题的关键．‎ ‎　‎ ‎18．（3分）（2015•威海）如图①，②，③，用一种大小相等的正多边形密铺成一个“环”，我们称之为环形密铺．但图④，⑤不是我们所说的环形密铺．请你再写出一种可以进行环形密铺的正多边形：　正十二边形　．‎ 考点：‎ 平面镶嵌（密铺）．.‎ 分析：‎ 根据环形密铺的定义，所用多边形的外角的2倍是正多边形的内角即可．‎ 解答：‎ 解：正十二边形的外角是360°÷12=30°，‎ ‎∵30°×2=60°是正三角形，‎ ‎∴正十二边形可以进行环形密铺．‎ 故答案为：正十二边形．‎ 点评：‎ 本题考查了平面密铺，观察图形判断出中间空白正多边形的内角是所用正多边形的外角的2倍是解题的关键．‎ ‎　‎ 三、计算题 ‎19．（7分）（2015•威海）先化简，再求值：（）÷，其中x=﹣2+．‎ 考点：‎ 分式的化简求值．.‎ 分析：‎ 先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．‎ 解答：‎ 解：原式=÷‎ ‎=÷‎ ‎=•‎ ‎=‎ ‎=﹣，‎ 当x=﹣2+时，原式=﹣=﹣=﹣．‎ 点评：‎ 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．‎ ‎　‎ ‎20．（8分）（2015•威海）某学校为了推动球类运动的普及，成立多个球类运动社团，为此，学生会采取抽样调查的方法，从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好（要求每位同学只能选择其中一种自己喜欢的球类运动），并将调查结果绘制成了如下条形统计图和扇形统计图（不完整）．请你根据图中提供的信息，解答下列问题：‎ ‎（1）本次抽样调查，共调查了　400　名学生；‎ ‎（2）请将条形统计图和扇形统计图补充完整；‎ ‎（3）若该学校共有学生1800人，根据以上数据分析，试估计选择排球运动的同学约有多少人？‎ 考点：‎ 条形统计图；用样本估计总体；扇形统计图．.‎ 分析：‎ ‎（1）根据喜欢足球的人数与所占的百分比列式计算即可求出调查的学生总人数；‎ ‎（2）分别计算出乒乓球、篮球的人数、篮球所占的百分比、排球所占的百分比，即可补全统计图；‎ ‎（3）用1800×选择排球运动的百分比，即可解答．‎ 解答：‎ 解：（1）100÷25%=400（人），‎ ‎∴本次抽样调查，共调查了400名学生；‎ 故答案为：400．‎ ‎（2）乒乓球的人数：400×40%=160（人），篮球的人数：400﹣100﹣160﹣40=100（人），‎ 篮球所占的百分比为：=25%，排球所占的百分比为：×100%=10%，‎ 如图所示：‎ ‎（3）1800×10%=180（人），‎ ‎∴若该学校共有学生1800人，根据以上数据分析，试估计选择排球运动的同学约有180人．‎ 点评：‎ 本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ ‎　‎ ‎21．（9分）（2015•威海）为绿化校园，某校计划购进A、B两种树苗，共21课．已知A种树苗每棵90元，B种树苗每棵70元．设购买B种树苗x棵，购买两种树苗所需费用为y元．‎ ‎（1）y与x的函数关系式为：　y=﹣20x+1890　；‎ ‎（2）若购买B种树苗的数量少于A种树苗的数量，请给出一种费用最省的方案，并求出该方案所需费用．‎ 考点：‎ 一次函数的应用．.‎ 分析：‎ ‎（1）根据购买两种树苗所需费用=A种树苗费用+B种树苗费用，即可解答；‎ ‎（2）根据购买B种树苗的数量少于A种树苗的数量，列出不等式，确定x的取值范围，再根据（1）得出的y与x之间的函数关系式，利用一次函数的增减性结合自变量的取值即可得出更合算的方案．‎ 解答：‎ 解：（1）y=90（21﹣x）+70x=﹣20x+1890，‎ 故答案为：y=﹣20x+1890．‎ ‎（2）∵购买B种树苗的数量少于A种树苗的数量，‎ ‎∴x＜21﹣x，‎ 解得：x＜10.5，‎ 又∵x≥1，‎ ‎∴x的取值范围为：1≤x≤10，且x为整数，‎ ‎∵y=﹣20x+1890，k=﹣20＜0，‎ ‎∴y随x的增大而减小，‎ ‎∴当x=10时，y有最小值，最小值为：﹣20×10+1890=1690，‎ ‎∴使费用最省的方案是购买B种树苗10棵，A种树苗11棵，所需费用为1690元．‎ 点评：‎ 题考查的是一元一次不等式及一次函数的应用，解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的等量关系和不等关系．‎ ‎　‎ ‎22．（9分）（2015•威海）如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．‎ ‎（1）求证：BE=CE；‎ ‎（2）若BD=2，BE=3，求AC的长．‎ 考点：‎ 相似三角形的判定与性质；等腰三角形的性质；圆周角定理．.‎ 专题：‎ 证明题．‎ 分析：‎ ‎（1）连结AE，如图，根据圆周角定理，由AC为⊙O的直径得到∠AEC=90°，然后利用等腰三角形的性质即可得到BE=CE；‎ ‎（2）连结DE，如图，证明△BED∽△BAC，然后利用相似比可计算出AB的长，从而得到AC的长．‎ 解答：‎ ‎（1）证明：连结AE，如图，‎ ‎∵AC为⊙O的直径，‎ ‎∴∠AEC=90°，‎ ‎∴AE⊥BC，‎ 而AB=AC，‎ ‎∴BE=CE；‎ ‎（2）连结DE，如图，‎ ‎∵BE=CE=3，‎ ‎∴BC=6，‎ ‎∵∠BED=∠BAC，‎ 而∠DBE=∠CBA，‎ ‎∴△BED∽△BAC，‎ ‎∴=，即=，‎ ‎∴BA=9，‎ ‎∴AC=BA=9．‎ 点评：‎ 本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．也考查了角平分线的性质和圆周角定理．‎ ‎　‎ ‎23．（10分）（2015•威海）（1）如图1，已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°，求AD的长．‎ ‎（2）如图2，已知∠ACB=∠DCE=90°，∠ABC=∠CED=∠CAE=30°，AC=3，AE=8，求AD的长．‎ 考点：‎ 相似三角形的判定与性质；全等三角形的判定与性质；勾股定理．.‎ 分析：‎ ‎（1）连接BE，证明△ACD≌△BCE，得到AD=BE，在Rt△BAE中，AB=6，AE=3，求出BE，得到答案；‎ ‎（2）连接BE，证明△ACD∽△BCE，得到==，求出BE的长，得到AD的长．‎ 解答：‎ 解：（1）如图1，连接BE，‎ ‎∵∠ACB=∠DCE=90°，‎ ‎∴∠ACB+∠ACE=∠DCE+∠ACE，即∠BCE=∠ACD，‎ 又∵AC=BC，DC=EC，‎ 在△ACD和△BCE中，‎ ‎，‎ ‎∴△ACD≌△BCE，‎ ‎∴AD=BE，‎ ‎∵AC﹣BC=6，‎ ‎∴AB=6，‎ ‎∵∠BAC=∠CAE=45°，‎ ‎∴∠BAE=90°，‎ 在Rt△BAE中，AB=6，AE=3，‎ ‎∴BE=9，‎ ‎∴AD=9；‎ ‎（2）如图2，连接BE，‎ 在Rt△ACB中，∠ABC=∠CED=30°，‎ tan30°==，‎ ‎∵∠ACB=∠DCE=90°，‎ ‎∴∠BCE=∠ACD，‎ ‎∴△ACD∽△BCE，‎ ‎∴==，‎ ‎∵∠BAC=60°，∠CAE=30°，‎ ‎∴∠BAE=90°，又AB=6，AE=8，‎ ‎∴BE=10，‎ ‎∴AD=．‎ 点评：‎ 本题考查的是相似三角形的判定和性质、全等三角形的判定和性质，掌握性质定理和判定定理是解题的关键，正确作出辅助线是重点．‎ ‎　‎ ‎24．（11分）（2015•威海）如图1，直线y=k1x与反比例函数y=（k≠0）的图象交于点A，B，直线y=k2x与反比例函数y=的图象交于点C，D，且k1•k2≠0，k1≠k2，顺次连接A，D，B，C，AD，BC分别交x轴于点F，H，交y轴于点E，G，连接FG，EH．‎ ‎（1）四边形ADBC的形状是　平行四边形　；‎ ‎（2）如图2，若点A的坐标为（2，4），四边形AEHC是正方形，则k2=　　；‎ ‎（3）如图3，若四边形EFGH为正方形，点A的坐标为（2，6），求点C的坐标；‎ ‎（4）判断：随着k1、k2取值的变化，四边形ADBC能否为正方形？若能，求点A的坐标；若不能，请简要说明理由．‎ 考点：‎ 反比例函数综合题．.‎ 分析：‎ ‎（1）直接根据正比例函数与反比例函数的性质即可得出结论；‎ ‎（2）过点A作AM⊥y轴，垂足为M，过点C作CN⊥x轴，垂足为N，根据四边形AEHC是正方形可知OA=OC，故可得出△OAM≌△OCN，AM=CN，由此可得出C点坐标，由此可得出C点坐标，利用待定系数法求出k2的值即可；‎ ‎（3）过点A作AM⊥y轴，垂足为M，过点C作CN⊥x轴，垂足为N，根据四边形EFGH为正方形可得出AM=AE．CN=HN．由点A（2，6）得出AM=ME=2，OM=6，设CN=HN=m，则点C的坐标为（4+m，m）．根据反比例函数y=的图象过点C和点A（2，6）可得出m的值，进而可得出结论；‎ ‎（4）根据反比例函数y=（k≠0）的图象不能与坐标轴相交可知∠AOC＜90°，故四边形ADBC的对角线不能互相垂直，由此可得出结论．‎ 解答：‎ 解：（1）∵正比例函数与反比例函数的图象均关于原点对称，‎ ‎∴OA=OB，OC=OD，‎ ‎∴四边形ADBC是平行四边形．‎ 故答案为：平行四边形；‎ ‎（2）如图1，过点A作AM⊥y轴，垂足为M，过点C作CN⊥x轴，垂足为N，‎ ‎∵四边形AEHC是正方形，‎ ‎∴DA⊥AC，‎ ‎∴四边形ADBC是矩形，‎ ‎∴OA=OC．‎ ‎∴AM=CN，‎ ‎∴C（4，2），‎ ‎∴2=4k2，解得k2=．‎ 故答案为；；‎ ‎（3）如图3所示，过点A作AM⊥y轴，垂足为M，过点C作CN⊥x轴，垂足为N，‎ ‎∵四边形EFGH为正方形，‎ ‎∴∠FEO=45°，EO=HO，‎ ‎∴∠AEM=45°．‎ ‎∵∠AME=90°，‎ ‎∴∠EAM=∠AEM=45°．‎ ‎∴AM=AE．‎ 同理，CN=HN．‎ ‎∵点A（2，6），‎ ‎∴AM=ME=2，OM=6，‎ ‎∴OE=OH=4．‎ 设CN=HN=m，则点C的坐标为（4+m，m）．‎ ‎∵反比例函数y=的图象过点C和点A（2，6），‎ ‎∴m•（4+m）=12，解得m1=2，m2=﹣6（舍去）；‎ 当m=2时，m+4=6，‎ ‎∴点C的坐标为（6，2）；‎ ‎（4）不能．‎ ‎∵反比例函数y=（k≠0）的图象不能与坐标轴相交，‎ ‎∴∠AOC＜90°，‎ ‎∴四边形ADBC的对角线不能互相垂直，‎ ‎∴四边形ADBC不能是正方形．‎ 点评：‎ 本题考查的是反比例函数综合题，涉及到反比例函数与正比例函数的性质、正方形的性质等知识，难度适中．‎ ‎　‎ ‎25．（12分）（2015•威海）已知：抛物线l1：y=﹣x2+bx+3交x轴于点A，B，（点A在点B的左侧），交y轴于点C，其对称轴为x=1，抛物线l2经过点A，与x轴的另一个交点为E（5，0），交y轴于点D（0，﹣）．‎ ‎（1）求抛物线l2的函数表达式；‎ ‎（2）P为直线x=1上一动点，连接PA，PC，当PA=PC时，求点P的坐标；‎ ‎（3）M为抛物线l2上一动点，过点M作直线MN∥y轴，交抛物线l1于点N，求点M自点A运动至点E的过程中，线段MN长度的最大值．‎ 考点：‎ 二次函数综合题．.‎ 分析：‎ ‎（1）由对称轴可求得b，可求得l1的解析式，令y=0可求得A点坐标，再利用待定系数法可求得l2的表达式；‎ ‎（2）设P点坐标为（1，y），由勾股定理可表示出PC2和PA2，由条件可得到关于y的方程可求得y，可求得P点坐标；‎ ‎（3）可分别设出M、N的坐标，可表示出MN，再根据函数的性质可求得MN的最大值．‎ 解答：‎ 解：（1）∵抛物线l1：y=﹣x2+bx+3的对称轴为x=1，‎ ‎∴﹣=1，解得b=2，‎ ‎∴抛物线l1的解析式为y=﹣x2+2x+3，‎ 令y=0，可得﹣x2+2x+3=0，解得x=﹣1或x=3，‎ ‎∴A点坐标为（﹣1，0），‎ ‎∵抛物线l2经过点A、E两点，‎ ‎∴可设抛物线l2解析式为y=a（x+1）（x﹣5），‎ 又∵抛物线l2交y轴于点D（0，﹣），‎ ‎∴﹣=﹣5a，解得a=，‎ ‎∴y=（x+1）（x﹣5）=x2﹣2x﹣，‎ ‎∴抛物线l2的函数表达式为y=x2﹣2x﹣；‎ ‎（2）设P点坐标为（1，y），由（1）可得C点坐标为（0，3），‎ ‎∴PC2=12+（y﹣3）2=y2﹣6y+10，PA2=[1﹣（﹣1）]2+y2=y2+4，‎ ‎∵PC=PA，‎ ‎∴y2﹣6y+10=y2+4，解得y=1，‎ ‎∴P点坐标为（1，1）；‎ ‎（3）由题意可设M（x，x2﹣2x﹣），‎ ‎∵MN∥y轴，‎ ‎∴N（x，﹣x2+2x+3），x2﹣2x﹣‎ 令﹣x2+2x+3=x2﹣2x﹣，可解得x=﹣1或x=，‎ ‎①当﹣1＜x≤时，MN=（﹣x2+2x+3）﹣（x2﹣2x﹣）=﹣x2+4x+=﹣（x﹣）2+，‎ 显然﹣1＜≤，∴当x=时，MN有最大值；‎ ‎②当＜x≤5时，MN=（x2﹣2x﹣）﹣（﹣x2+2x+3）=x2﹣4x﹣=（x﹣）2﹣，‎ 显然当x＞时，MN随x的增大而增大，‎ ‎∴当x=5时，MN有最大值，×（5﹣）2﹣=12；‎ 综上可知在点M自点A运动至点E的过程中，线段MN长度的最大值为12．‎ 点评：‎ 本题主要考查二次函数的综合应用，涉及待定系数法、二次函数的性质、勾股定理等知识点．在（1）中求得A点的坐标是解题的关键，在（2）中用P点的坐标分别表示出PA、PC是解题的关键，在（3）中用M、N的坐标分别表示出MN的长是解题的关键，注意分类讨论．本题考查知识点较为基础，难度适中．‎