南通市2013年中考数学卷 13页

‎2013年中考数学试题（江苏南通卷）‎ ‎（本试卷满分150分，考试时间120分钟）‎ 一、选择题（本大题共10小题，每小题3分，满分30分）‎ ‎1．下列各数中，小于－3的数是【 】‎ A．2 B．‎1 C．－2 D．－4‎ ‎【答案】D。‎ ‎2．某市2013年参加中考的考生人数约为85000人，将85000用科学记数法表示为【 】‎ A． B． C． D．‎ ‎【答案】A。‎ ‎3．下列计算，正确的是【 】‎ A． B． C． D．‎ ‎【答案】C。‎ ‎4．下面的几何体中，既是轴对称图形又是中心对称图形的个数是【 】‎ A．4 B．‎3 C．2 D．1‎ ‎【答案】C。‎ ‎5．有‎3cm，‎6cm，‎8cm，‎9cm的四条线段，任选其中的三条线段组成一个三角形，则最多能组成三角形的个数为【 】‎ A．1 B．‎2 C．3 D．4‎ ‎【答案】C。‎ ‎6．函数中，自变量x的取值范围是【 】‎ A．x＞1 B．x≥‎1 C．x＞－2 D．x≥―2‎ ‎【答案】A。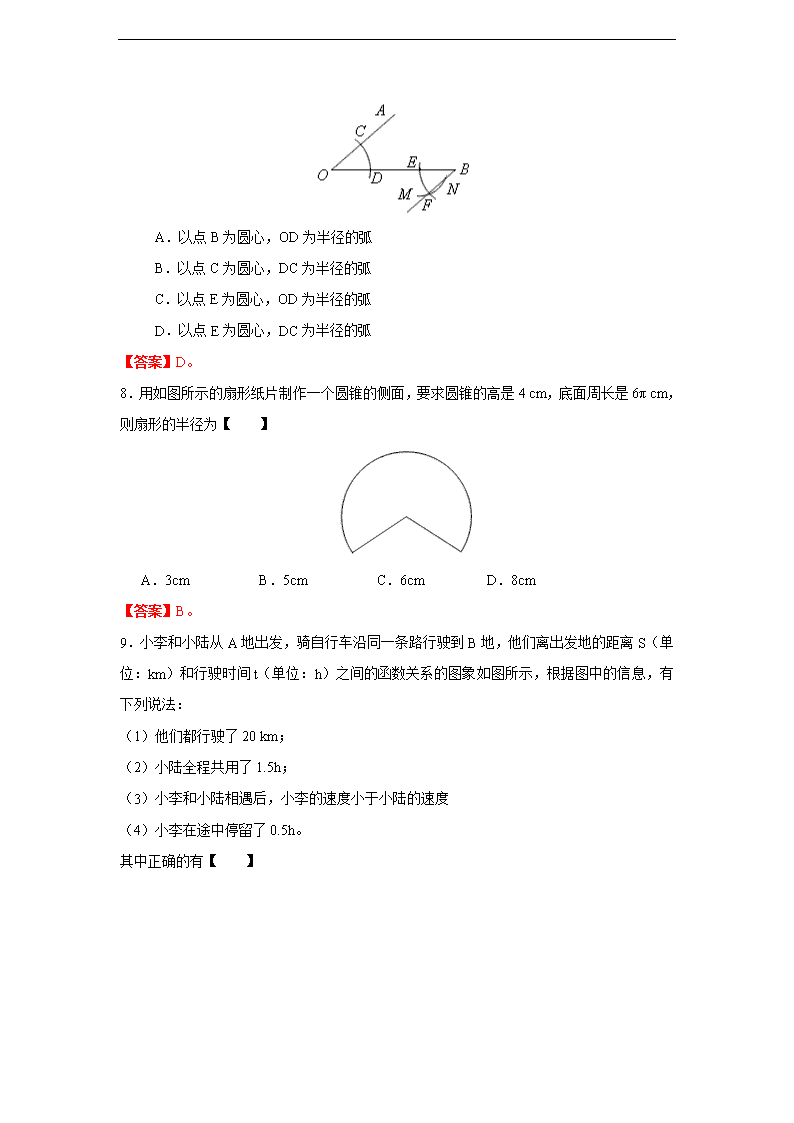‎ ‎7．如图，用尺规作出∠OBF=∠AOB，所画痕迹是【 】‎ ‎ A．以点B为圆心，OD为半径的弧 B．以点C为圆心，DC为半径的弧 C．以点E为圆心，OD为半径的弧 D．以点E为圆心，DC为半径的弧 ‎【答案】D。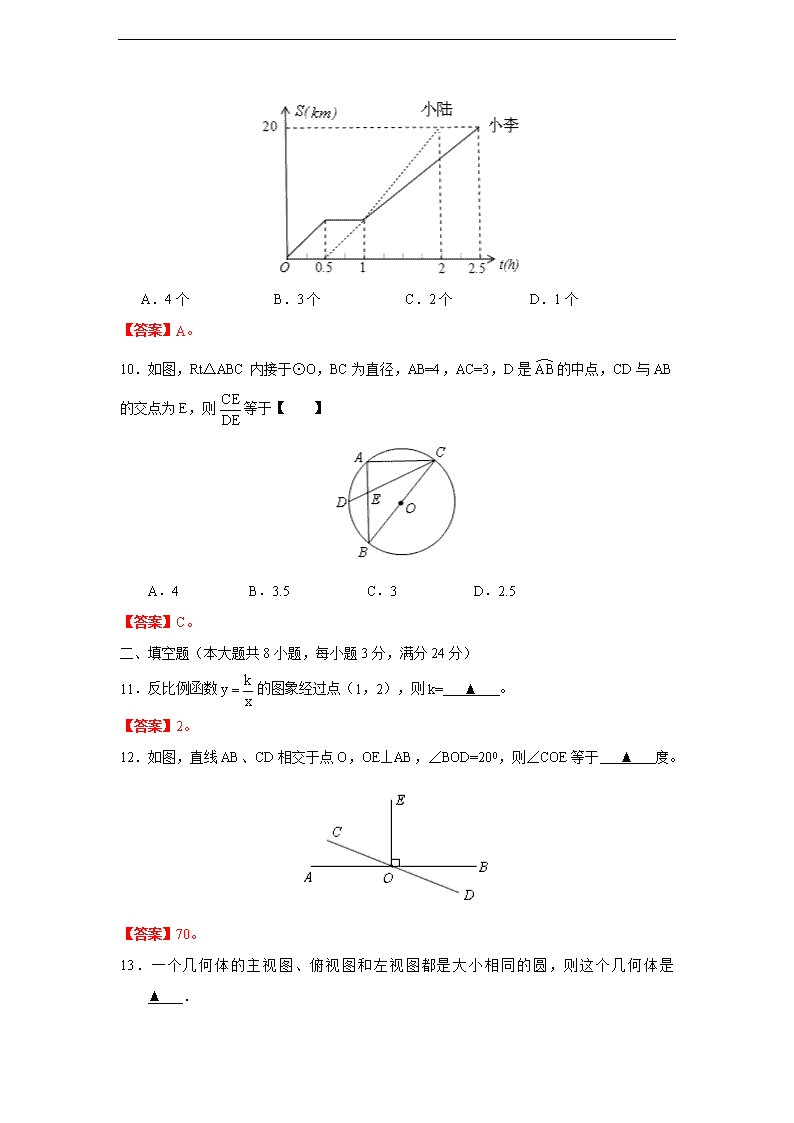‎ ‎8．用如图所示的扇形纸片制作一个圆锥的侧面，要求圆锥的高是‎4 cm，底面周长是6π cm，则扇形的半径为【 】‎ A．‎3cm B．‎5cm C．‎6cm D．‎‎8cm ‎【答案】B。‎ ‎9．小李和小陆从A地出发，骑自行车沿同一条路行驶到B地，他们离出发地的距离S（单位：km）和行驶时间t（单位：h）之间的函数关系的图象如图所示，根据图中的信息，有下列说法：‎ ‎（1）他们都行驶了‎20 km；‎ ‎（2）小陆全程共用了1.5h；‎ ‎（3）小李和小陆相遇后，小李的速度小于小陆的速度 ‎（4）小李在途中停留了0.5h。‎ 其中正确的有【 】‎ A．4个 B．3个 C．2个 D．1个 ‎【答案】A。‎ ‎10．如图，Rt△ABC内接于⊙O，BC为直径，AB=4，AC=3，D是的中点，CD与AB的交点为E，则等于【 】‎ A．4 B．‎3.5 C．3 D．2.5‎ ‎【答案】C。‎ 二、填空题（本大题共8小题，每小题3分，满分24分）‎ ‎11．反比例函数的图象经过点（1，2），则k= ▲ 。‎ ‎【答案】2。‎ ‎12．如图，直线AB、CD相交于点O，OE⊥AB，∠BOD=200，则∠COE等于 ▲ 度。‎ ‎【答案】70。‎ ‎13．一个几何体的主视图、俯视图和左视图都是大小相同的圆，则这个几何体是 ▲ ．‎ ‎【答案】球。‎ ‎14．如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=2，AC=3，则sinB的值是 ▲ 。‎ ‎【答案】。‎ ‎15．已知一组数据5，8，10，x，9的众数是8，那么这组数据的方差是 ▲ 。‎ ‎【答案】。‎ ‎16．如图，经过点B（－2，0）的直线与直线相交于点A（－1，－2），则不等式的解集为 ▲ 。 ‎ ‎【答案】。‎ ‎17．如图，在ABCD中，AB=‎6cm，AD=‎9cm，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=cm，则EF＋CF的长为 ▲ cm。‎ ‎【答案】5。‎ ‎18．已知和时，多项式的值相等，且，则当时，多项式的值等于 ▲ 。‎ ‎【答案】3。‎ 三、解答题（本大题共10小题，满分96分）‎ ‎19． ‎ ‎（1）计算：。 ‎ ‎【答案】解：原式=2＋1－3=0。‎ ‎（2）先化简，再求代数式的值： ，其中m＝1。‎ ‎【答案】解：原式= 。‎ ‎ 当m＝1时，原式= 。‎ ‎20．在平面直角坐标系xOy中，已知A（－1，5），B（4，2），C（－1，0）三点。‎ ‎（1）点A关于原点O的对称点A′的坐标为 ▲ ，点B关于x轴对称点B′的坐标为 ▲ ，点C关于y轴对称点C′的坐标为 ▲ ；‎ ‎（2）求（1）中的△A′B′C′的面积。‎ ‎【答案】解：（1）（1，－5）；（4，－2）；（1，0）。‎ ‎ （2）如图，△A′B′C′的面积。‎ ‎21．某水果批发市场将一批苹果分为A，B，C，D四个等级，统计后将结果绘成条形图，已知A等级苹果的重量占这批苹果总重量的30%。回答下列问题：‎ ‎（1）这批苹果总重量为 ▲ kg；‎ ‎（2）请将条形图补充完整；‎ ‎（3）若用扇形图表示统计结果，则C等级苹果所对应扇形圆心角为 ▲ 度。‎ ‎【答案】解：（1）4000。‎ ‎（2）条形图补充完整如下：‎ ‎（3）90。‎ ‎22．在不透明的袋子中有四张标有数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏。‎ 小明画出树形图如下：‎ 小华列出表格如下：‎ ‎ 第一次 第二次 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎（1，1）‎ ‎（2，1）‎ ‎（3，1）‎ ‎（4，1）‎ ‎2‎ ‎（1，2）‎ ‎（2，2）‎ ‎①‎ ‎（4，2）‎ ‎3‎ ‎（1，3）‎ ‎（2，3）‎ ‎（3，3）‎ ‎（4，3）‎ ‎4‎ ‎（1，4）‎ ‎（2，4）‎ ‎（3，4）‎ ‎（4，4）‎ 回答下列问题：‎ ‎（1）根据小明画出的树形图分析，他的游戏规则是：随机抽出一张卡片后 ▲ （填“放回”或“不放回”），再随机抽出一张卡片；‎ ‎（2）根据小华的游戏规则，表格中①表示的有序数对为 ▲ ；‎ ‎（3）规定两次抽到的数字之和为奇数的获胜，你认为淮获胜的可能性大？为什么？‎ ‎【答案】解：（1）放回。‎ ‎（2）（3，2）。‎ ‎（3）理由如下：‎ ‎ ∵根据小明的游戏规则，共有12种等可能结果，数字之和为奇数的有8种，‎ ‎ ∴概率为：。‎ ‎ ∵根据小华的游戏规则，共有16种等可能结果，数字之和为奇数的有8种，‎ ‎ ∴概率为：。‎ ‎ ∵，∴小明获胜的可能性大。‎ ‎23．若关于x的不等式组恰有三个整数解，求实数a的取值范围。‎ ‎【答案】解：解得：；‎ ‎　　　　　　解得：。‎ ‎　　　　　　∴不等式组的解为。‎ ‎　　　　　　∵关于x的不等式组恰有三个整数解，‎ ‎　　　　　　∴，解得。‎ ‎∴实数a的取值范围为。‎ ‎24．如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE。‎ 求证：四边形BCDE是矩形。‎ ‎【答案】证明：∵∠BAD=∠CAE，∴∠BAE=∠CAD。‎ 在△ABE和△ACD中，‎ ‎∵AB=AC，AE=AD，∠BAE=∠CAD，∴△ABE≌△ACD（SAS）.‎ ‎∴BE=CD。‎ 又∵DE=BC，∴四边形BCDE为平行四边形。‎ 如图，连接BD,AC,‎ 在△ACE和△ABD中，‎ ‎∵AC=AB，AE=AD，∠CAE=∠BAD，‎ ‎∴△ACE≌△ABD（SAS），∴CE=BD。‎ ‎∴四边形BCED为矩形（对角线相等的平行四边形是矩形）.‎ ‎25．如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC=2∠B，⊙O的切线AP与OC的延长线相交于点P。若，求AC的长。‎ ‎【答案】解：∵AB是⊙O的直径，∴∠ACB=900。‎ 又∵∠BAC=2∠B，∴∠B=300，∠BAC=600。‎ 又∵OA=OC，∴△OAC是等边三角形。∴∠AOC=600。‎ ‎∵PA是⊙O的切线，∴∠OAP=900。‎ 在中，，∠AOP=600，∴。‎ ‎∴AC=OA=6。‎ ‎26．某公司营销A，B两种产品，根据市场调研，发现如下信息：‎ 信息1：销售A种产品所获利润ｙ（万元）与所售产品x（吨）之间存在二次函数关系。‎ 当x＝1时，ｙ＝1.4；当x＝3时，ｙ＝3.6。‎ 信息2：销售B种产品所获利润ｙ（万元）与所售产品x（吨）之间存在正比例函数关系。‎ 根据以上信息，解答下列问题：‎ ‎（1）求二次函数解析式；‎ ‎（2）该公司准备购进A，B两种产品共10吨，请设计一个营销方案，使销售A，B两种产品获得的利润之和最大，最大利润是多少？‎ ‎【答案】解：（1）将（1，1.4），（3，3.6）代入，得 ‎，解得。‎ ‎∴二次函数解析式为。‎ ‎（2）设购进A产品m吨，购进B产品10－m吨，销售A，B两种产品获得的利润之和为W万元。则 ‎ ‎ ‎　 　∵，∴当m＝6时，W有最大值6.6。‎ ‎∴购进A产品6吨，购进B产品4吨，销售A，B两种产品获得的利润之和最大，最大利润是6.6万元。‎ ‎27．如图，在Rt△ABC中，∠ACB=900，AC=，BC=3，△DEF是边长为a（a为小于3的常数）的等边三角形，将△DEF沿AC方向平移，使点D在线段AC上，DE∥AB，设△DEF与△ABC重叠部分的周长为T。‎ ‎（1）求证：点E到AC的距离为一常数；‎ ‎（2）若AD=，当a=2时，求T的值；‎ ‎（3）若点D运动到AC的中点处，请用含a的代数式表示T。‎ ‎【答案】解：（1）证明：如图，过点E作EH⊥AC于点H，则EH即为点E到AC的距离。‎ ‎∵在Rt△ABC中，∠ACB=900，AC=，BC=3，‎ ‎∴。∴∠A=600。‎ ‎∵DE∥AB，∴∠EDH=∠A=600。‎ ‎∵DE=a（a为小于3的常数），‎ ‎∴（常数）。‎ ‎∴点E到AC的距离为一常数。‎ ‎（2）当a=2时，。‎ ‎ ∵AD=，∴AH=。∴此时，点H在在线段AC上。‎ ‎　　∴此时，△DEF与△ABC重叠部分就是△DEF。‎ ‎　　∴。‎ ‎（3）当点D运动到AC的中点处时， ，‎ 由得，，解得。‎ ‎∴分两种情况：‎ ‎①当时，点H在线段AC上，此时，△DEF与△ABC重叠部分就是△DEF。‎ ‎∴。‎ ‎②当时，点H在线段AC的延长线上，如图，此时，△DEF与△ABC重叠部分就是△DCG。‎ 根据三角形中位线定理，点G是BC的中点，‎ ‎∴CD=，CG=,DG=。‎ ‎∴。‎ 综上所述，。‎ ‎28．如图，直线与抛物线相交于A，B两点，与x轴正半轴相交于点D，与y轴相交于点C，设△OCD的面积为S，且。‎ ‎（1）求b的值；‎ ‎（2）求证：点在反比例函数的图象上；‎ ‎（3）求证：。‎ ‎【答案】解：（1）∵直线与x轴正半轴相交于点D，与y轴相交于点C，‎ ‎ ∴令x=0，得；令y=0，得。∴OC=，OD=。‎ ‎ ∴△OCD的面积。‎ ‎ ∵，∴，解得。‎ ‎ ∵ ，∴。‎ ‎ （2）证明：由（1），直线解析式为，即，代入，得，‎ ‎ 整理，得。‎ ‎ ∵直线与抛物线相交于A，B，‎ ‎ ∴，是方程的两个根。‎ ‎ ∴根据一元二次方程根与系数的关系，得。‎ ‎ ∴点在反比例函数的图象上。‎ ‎（3）证明：由勾股定理，得，‎ ‎ 由（2）得。‎ ‎ 同理，将代入，得，即，∴。‎ ‎ ∴。‎ ‎ 又，∴。‎ ‎ ∴△OAB是直角三角形，即∠AOB=900。‎ ‎ 如图，过点A作AE⊥x轴于点E，过点B作BF⊥x轴于点F，‎ ‎ ∵∠AOB=900，‎ ‎ ∴∠AOE=900-∠BOF=∠OBF。‎ ‎ 又∵∠AEO =∠OFB=900，‎ ‎ ∴△AEO∽△OFB。∴。‎ ‎ ∵OE=，BF=，∴。‎ ‎ ∴。‎