中考全等三角形综合测试题 45页

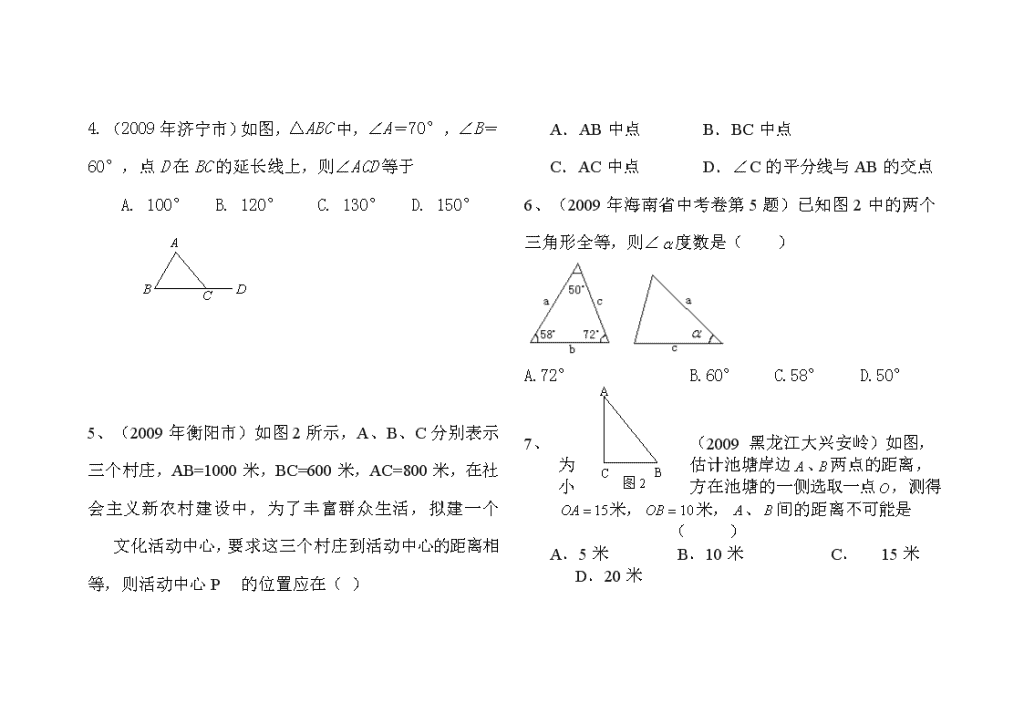
中考试题专题之三角形与全等三角形试题及答案 一、选择题 ‎1．（2009年江苏省）如图，给出下列四组条件：‎ ‎①；‎ ‎②；‎ ‎③；‎ ‎④．‎ 其中，能使的条件共有（ ）‎ A．1组 B．2组 C．3组 D．4组 ‎2.（2009年浙江省绍兴市）如图，分别为的，边的中点，将此三角形沿折叠，使点落在边上的点处．若，则等于（ ）‎ A． B． C ． D．‎ ‎ 3. (2009年义乌)如图，在中，，EF//AB,,则的度数为 ‎ A． B. C. D. ‎ ‎ ‎ ‎【关键词】三角形内角度数 ‎【答案】D ‎4.（2009年济宁市）如图，△ABC中，∠A＝70°，∠B＝60°，点D在BC的延长线上，则∠ACD等于 A. 100° B. 120° C. 130° D. 150°‎ ‎ ‎ A C B 图2 ‎ ‎5、（2009年衡阳市）如图2所示，A、B、C分别表示三个村庄，AB=‎1000米，BC=‎600米，AC=‎800米，在社会主义新农村建设中，为了丰富群众生活，拟建一个 文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P 的位置应在（ ）‎ ‎ A．AB中点 B．BC中点 ‎ C．AC中点 D．∠C的平分线与AB的交点 ‎6、（2009年海南省中考卷第5题）已知图2中的两个三角形全等，则∠度数是（ ）‎ A.72° B.60° C.58° D.50°‎ ‎7、（2009 黑龙江大兴安岭）如图，为估计池塘岸边、两点的距离，小方在池塘的一侧选取一点，测得米，米，、间的距离不可能是 （ ）‎ A．‎5米 B．‎10米 C． ‎15米 D．‎‎20米 ‎【‎ ‎8、（2009年崇左）一个等腰三角形的两边长分别为2和5，则它的周长为（ ）‎ A．7 B．‎9 C．12 D．9或12‎ ‎9、（2009年湖北十堰市）下列命题中，错误的是（ ）．‎ A．三角形两边之和大于第三边 ‎ B．三角形的外角和等于360°‎ C．三角形的一条中线能将三角形面积分成相等的两部分 D．等边三角形既是轴对称图形，又是中心对称图形 A D C E B ‎10、（09湖南怀化）如图，在中，o ‎90‎ = Ð B ，是的垂直平分线，交于点，交于点．已知，则的度数为（ ）‎ A． B． ‎ C． D．‎ ‎11、（2009年清远）如图，，于交于，已知，则（ ）‎ A．20° B．60° C．30° D．45°‎ C D B A E F ‎1‎ ‎2‎ ‎12、（2009年广西钦州）如图，在等腰梯形ABCD中，AB＝DC，AC、BD交于点O，则图中全等三角形共有（ ）‎ ‎ A．2对 B．3对 ‎ C．4对 D．5对 ‎【形 ‎13、(2009年甘肃定西)如图4，四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE=（　　）‎ A．2 B．‎3 ‎ C． D．‎ ‎14、（2009年广西钦州）如图，AC＝AD，BC＝BD，则有（ ）‎ ‎ A．AB垂直平分CD B．CD垂直平分AB ‎ C．AB与CD互相垂直平分 D．CD平分∠ACB ‎15、（2009肇庆）如图，中，，DE 过点C，且，若，则∠B的度数是（ ）‎ A．35° B．45° C．55° D．65° ‎ A B C D E ‎16、（2009年邵阳市）如图，将Rt△ABC(其中∠B＝34，∠C＝90）绕A点按顺时针方向旋转到△AB‎1 C1的位置，使得点C、A、B1　在同一条直线上，那么旋转角最小等于（　　）‎ ‎　　　A.56 B.68 C.124 　 D.180‎ ‎34‎ B1‎ C B A C1‎ ‎17、（2009年湘西自治州）一个角是80°，它的余角是（　　）‎ A．10° B．100° C．80° D．120°‎ ‎18、（2009河池）C B F A E 如图，在Rt△ABC中，，AB=AC＝，点E 为AC的中点，点F在底边BC上，且，则△‎ 的面积是（ ）‎ A． 16 B． ‎18 C． D． ‎ C D B A ‎19、（2009柳州）如图所示，图中三角形的个数共有（ ）‎ A．1个 B．2个 C．3 个 D．4个 ‎2‎ ‎12‎ C D B A ‎20、（2009年牡丹江）如图， 中，于一定能确定为直角三角形的条件的个数是（ ）‎ ‎①②③④‎ ‎⑤‎ A．1　 B．‎2 C．3 D．4‎ ‎【‎ ‎21、（2009桂林百色）如图所示，在方格纸上建立的平面直角坐标系中，‎ 将△ABO绕点O按顺时针方向旋转90°，‎ 得 ，则点的坐标为（ ）． ‎ A．（3，1） B．（3，2）C．（2，3） D．（1，3）‎ ‎22、（2009年长沙）已知三角形的两边长分别为‎3cm和‎8cm，则此三角形的第三边的长可能是（ ） ‎ A．‎4cm B．‎5cm C．‎6cm D．‎‎13cm ‎23、（2009年湖南长沙）已知三角形的两边长分别为‎3cm和‎8cm，则此三角形的第三边的长可能是（ ）‎ A．‎4cm B．‎5cm C．‎6cm D．‎‎13cm ‎24、（2009陕西省太原市）如图，，=30°，则的度数为（ ）‎ ‎ A．20° B．30° C．35° D．40°‎ C A B ‎25、 （2009陕西省太原市）如果三角形的两边分别为3和5，那么连接这个三角形三边中点，所得的三角形的周长可能是（ ）‎ A．4 B．‎4.5 C．5 D．5.5‎ ‎26、（2009年牡丹江）尺规作图作的平分线方法如下：以为圆心，任意长为半径画弧交、于、，再分别以点、为圆心，以大于长为半径画弧，两弧交于点，作射线由作法得的根据是（ ）‎ A．SAS B．ASA C．AAS　　D．SSS ‎27、（2009年新疆）如图，将三角尺的直角顶点放在直尺的一边上，，则的度数等于（ ）‎ A． B． C． D．‎ ‎1‎ ‎2‎ ‎3‎ ‎28、(2009年牡丹江市)尺规作图作的平分线方法如下：以为圆心，任意长为半径画弧交、于、，再分别以点、为圆心，以大于长为半径画弧，两弧交于点，作射线由作法得的根据是（ ）‎ A．SAS B．ASA C．AAS　　D．SSS ‎ O D P C A B ‎【‎ ‎29、（2009年包头）已知在中，，则的值为（ ）‎ A． B． C． D．‎ ‎【‎ ‎30、（2009年齐齐哈尔市）如图，为估计池塘岸边的距离，小方在池塘的一侧选取一点，测得米，=‎10米，间的距离不可能是（ ）‎ A．‎20米 B．‎15米 C．‎10米 D．‎‎5米 O A B ‎31、（2009年台湾）图(三)、图(四)、图(五)分别表示甲、乙、丙三人由A地到B地的路线图。已知 ‎ 甲的路线为：A®C®B。‎ ‎ 乙的路线为：A®D®E®F®B，其中E为的中点。‎ ‎ 丙的路线为：A®I®J®K®B，其中J在上，且>。‎ ‎ 若符号「®」表示「直线前进」，则根据图(三)、图 ‎(四)、图(五)的数据，判断三人行进路线 ‎ 长度的大小关系为何？‎ A B C A B D A B I ‎50° E F ‎60° ‎70° ‎50° ‎60° ‎70° ‎50° ‎60° ‎70° ‎50° ‎60° ‎70° ‎50° ‎60° ‎70° J K 圖(三)‎ 圖(四)‎ 圖(五)‎ ‎ ‎ ‎ (A) 甲=乙=丙 (B) 甲<乙<丙 (C) 乙<丙<甲 (D )丙<乙<甲 。‎ ‎32、（2009年娄底）如图1，已知AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是 ( ) A．63° B．83° C．73° D．53° ‎33、（2009烟台市）如图，等边的边长为3，为上一点，且，为上一点，若，则的长为（ ）‎ A． B． C． D．‎ ‎34、(2009武汉)在直角梯形中，，为边上一点，，且．连接交对角线于，连接．下列结论：‎ ‎①； ②为等边三角形； ③； ④．‎ 其中结论正确的是（ ）‎ A．只有①② B．只有①②④ C．只有③④ D．①②③④‎ D C B E A H ‎35、（2009年台湾） 若rABC中，ÐB为钝角，且=8，=6，则下列何者可能为之长度？‎ ‎ (A) 5 (B) 8 (C) 11 (D) 14 。‎ ‎36、（2009年重庆）观察下列图形，则第个图形中三角形的个数是（ ）‎ ‎……‎ 第1个 第2个 第3个 A． B． C． D．‎ ‎37、（2009年重庆）如图，在等腰中，‎ ‎，F是AB边上的中点，点D、E分别在AC、BC边上运动，且保持．连接DE、DF、EF．在此运动变化的过程中，下列结论：‎ ‎①是等腰直角三角形；‎ ‎②四边形CDFE不可能为正方形，‎ ‎③DE长度的最小值为4；‎ ‎④四边形CDFE的面积保持不变；‎ ‎⑤△CDE面积的最大值为8．‎ 其中正确的结论是（ ）‎ A．①②③ B．①④⑤ C．①③④ D．③④⑤‎ C E B A F D ‎【‎ A B C D ‎（第7题）‎ ‎38、（2009江西）如图，已知 那么添加下列一个条件后，‎ 仍无法判定的是（ ）‎ A．　　　　　　　 B．‎ C． D． ‎ ‎39、(2009年温州)下列长度的三条线段能组成三角形的是( )‎ ‎ A．‎1cm， ‎2cm， 3．‎5cm B．‎4cm， ‎5cm， 9cmC．‎5cm，‎8cm， ‎15cm D．‎6cm，‎8cm， ‎‎9cm ‎40、如图，OP平分，，，垂足分别为A，B．下列结论中不一定成立的是（ ）‎ A． B．平分 ‎ C． D．垂直平分 O B A P 二、填空题 ‎1、（2009年遂宁）如图，已知△ABC中，AB=‎5cm，BC=‎12cm，AC=‎13cm，那么AC边上的中线BD的长为 cm.‎ ‎2、（2009年遂宁）已知△ABC中，AB=BC≠AC，作与△ABC只有一条公共边，且与△ABC全等的三角形，这样的三角形一共能作出 个.‎ ‎3.（2009年济宁市）观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形有 个 ．‎ ‎4. (2009年四川省内江市)如图所示，将△ABC沿着DE翻折，若∠1+∠2=80O，则∠B=_____________。‎ ‎5、（2009年厦门市）如图，在ΔABC中，∠C=90°∠ABC的平分线BD交AC于点D,若BD=10厘米，BC=8厘米，则点D到直线AB的距离是__________厘米。‎ ‎6、（2009恩施市）如图1，已知，，，则的度数为________．‎ ‎7、（2009年吉林省）将一个含有60°角的三角板，按图所示的方式摆放在半圆形纸片上，为圆心，则= 度．‎ ‎8、（2009年包头）如图，已知与是两个全等的直角三角形，量得它们的斜边长为‎10cm，较小锐角为30°，将这两个三角形摆成如图（1）所示的形状，使点在同一条直线上，且点与点重合，将图（1）中的绕点顺时针方向旋转到图（2）的位置，点在边上，交于点，则线段的长为 cm（保留根号）．‎ C ‎(F)‎ D 图（2）‎ ‎9、（2009年长沙）如图，是的直径，是上一点，，则的度数为 ．答案：‎C B A O ‎10、（2009年甘肃白银）如图5，Rt△ACB中，∠ACB=90°，DE∥AB，若∠BCE=30°，则∠A=　　　　．‎ ‎ ‎ ‎11、（2009河池）如图2，的顶点坐标分别为．若将绕点顺时针旋转，得到，则点的对应点的坐标为 ．‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ O A B C y x 图2‎ ‎12、（2009河池）某小区有一块等腰三角形的草地，它的一边长为，‎ 面积为，为美化小区环境，现要给这块三角形草地围上白色的低矮栅栏，‎ 则需要栅栏的长度为　　　 m．‎ ‎13、（2009白银市）．如图5，Rt△ACB中，∠ACB=90°，DE∥AB，若∠BCE=30°，则∠A=　　　　．（缺图）‎ ‎14、 (2009宁夏)如图，的周长为32，且于，的周长为24，那么 的长为　　　　　　．‎ A B C D ‎15、（2009年郴州市）如图，桌面上平放着一块三角板和一把直尺，小明将三角板的直角顶点紧靠直尺的边缘，他发现无论是将三角板绕直角顶点旋转，还是将三角板沿直尺平移，与的和总是保持不变，那么与的和是_______度．‎ 三角形 ‎【‎ ‎16、（2009年常德市）已知△ABC中，BC=‎6cm，E、F分别是AB、AC的中点，那么EF长是 　　 cm．‎ ‎17、（2009年广西梧州）如图，△ABC中，∠A＝60°，‎ ‎∠C＝40°，延长CB到D ，则∠ABD＝ ★度．‎ A B C D ‎18、（2009年清远）如图，若，且，则= ．‎ A B C C1‎ A1‎ B1‎ ‎19、（09湖南邵阳）如图（四），点是菱形的对角线上的任意一点，连结 ．请找出图中一对全等三角形为___________．‎ A C E B D ‎20、（09湖南怀化）如图，已知，，要使 ≌，可补充的条件是 （写出一个即可）．‎ A D F C Ｂ Ｏ Ｅ ‎21、(2009年咸宁市)如图，在中，和的平分线相交于点，过点作交于，交 于，过点作于．下列四个结论：‎ ‎；‎ ‎②以为圆心、为半径的圆与以为圆心、为半径的圆外切；‎ ‎③设则；‎ ‎④不能成为的中位线．‎ 其中正确的结论是_____________．（把你认为正确结论的序号都填上）‎ ‎【‎ ‎22、(2009年达州)如图5，△ABC中，AB＝AC，与∠BAC相邻的外角为80°，则∠B＝____________.‎ ‎ ‎ ‎23、(2009年达州)长度为2㎝、3㎝、4㎝、5㎝的四条线段，从中任取三条线段能组成三角形的概率是______________.‎ ‎【关键词】三角形三边关系,概率 ‎【答案】‎ 三、解答题 ‎1、（2009年浙江省绍兴市）如图，在中，，分别以 为边作两个等腰直角三角形和，使．‎ ‎（1）求的度数；‎ ‎（2）求证：．‎ ‎ ‎ ‎2、（2009年宁波市）如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为，直线BC经过点，，将四边形OABC绕点O按顺时针方向旋转度得到四边形，此时直线、直线分别与直线BC相交于点P、Q．‎ ‎（1）四边形OABC的形状是 ，‎ 当时，的值是 ；‎ ‎（2）①如图2，当四边形的顶点落在轴正半轴时，求的值；‎ ‎②如图3，当四边形的顶点落在直线上时，求的面积．‎ ‎（Q）‎ B A O x P ‎（图3）‎ y Q C B A O x P ‎（图2）‎ y C B A O y x ‎（备用图）‎ ‎（第26题）‎ ‎（3）在四边形OABC旋转过程中，当时，是否存在这样的点P和点Q，使？若存在，请直接写出点P的坐标；若不存在，请说明理由．‎ ‎【答案】‎ 综．‎ ‎3、（2009年福州）如图，已知AC平分∠BAD，∠1=∠2，求证：AB=AD ‎4、（2009年宜宾）已知：如图，在四边形ABCD中，AB=CB,AD=CD。‎ ‎ 求证：∠C=∠A.‎ ‎5、(2009年安顺)如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连结BF。‎ （1） 求证：BD=CD；‎ （2） 如果AB=AC，试判断四边形AFBD的形状，并证明你的结论。‎ ‎【形．‎ ‎6、(2009年南充)如图，ABCD是正方形，点G是BC上的任意一点，于E，，交AG于F．‎ 求证：．‎ D C B A E F G ‎7、(2009年湖州)如图：已知在中，‎ ‎，为边的中点，过点作，‎ 垂足分别为.‎ （1） 求证：；‎ ‎（2）若，求证：四边形是正方形. ‎ D C B E A F ‎，为正方形．‎ ‎8、(2009年湖州)若P为所在平面上一点，且，则点叫做的费马点.‎ ‎（1）若点为锐角的费马点，且，则的值为________；‎ ‎（2）如图，在锐角外侧作等边′连结′.‎ 求证：′过的费马点，且′=.‎ A C B ‎9、（2009临沂）数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．，且EF交正方形外角的平行线CF于点F，求证：AE=EF．‎ 经过思考，小明展示了一种正确的解题思路：取AB 的中点M，连接ME，则AM=EC，易证，所以．‎ 在此基础上，同学们作了进一步的研究：‎ ‎（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；‎ ‎ （2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．‎ A D F C G E B 图1‎ A D F C G E B 图2‎ A D F C G E B 图3‎ ‎10、（2009年娄底）如图10，在△ABC中，AB=AC，D是BC的中点，连结AD，在AD的延长线上取一点E，连结BE，CE. ‎（1）求证：△ABE≌△ACE ‎（2）当AE与AD满足什么数量关系时，四边形ABEC是 菱形？并说明理由. ‎11、（2009丽水市）已知命题：如图，点A，D，B，E在同一条直线上，且AD=BE，∠A=∠FDE，则△ABC≌△DEF.判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题，请添加一个适当条件使它成为真命题,并加以证明.‎ ‎12、（2009烟台市）如图，直角梯形ABCD中，，，且，过点D作，交的平分线于点E，连接BE．‎ ‎（1）求证：；‎ ‎（2）将绕点C，顺时针旋转得到，连接EG.．求证：CD垂直平分EG.‎ ‎（3）延长BE交CD于点P．求证：P是CD的中点．‎ 即．‎A D G E C B ‎（2‎ ‎13、（2009恩施市）两个完全相同的矩形纸片、如图7放置，，求证：四边形为菱形．‎ ‎【答案】‎ C D E M A B F N ‎ ‎ ‎14、(2009年上海市)已知线段与相交于点，联结，为的中点，为的中点，联结（如图所示）．‎ O D C A B E F ‎（1）添加条件∠A=∠D，，求证：AB=DC．‎ ‎（2）分别将“”记为①，“”记为②，“”记为③，添加条件①、③，以②为结论构成命题1，添加条件②、③，以①为结论构成命题2．命题1是 命题，命题2是 命题（选择“真”或“假”填入空格）．‎ ‎15、(2009武汉)如图，已知点在线段上，BE=CF，AB∥DE，∠ACB=∠F．‎ 求证：．‎ C E B F D A ‎16、(2009年陕西省)如图，在□ABCD中，点E是AD的中点，连接CE并延长，交BA的延长线于点F．‎ 求证：FA＝AB．‎ ‎17、（2009年泸州）如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，‎ AD与BE相交于点F．‎ ‎ (1)求证：≌△CAD； ‎ ‎ (2)求∠BFD的度数．‎ A B D E C ‎18、 (2009年四川省内江市)如图，已知AB=AC，AD=AE，求证：BD=CE.‎ AE得∠ADE=∠AED ‎∴∠ADB=∠AEC ‎∴△ABD≌△ACE ‎∴BD=CE A B D E C F ‎19、 (2009年四川省内江市)如图，四边形ABCD内接于圆，对角线AC与BD相交于点E、F在AC上，AB=AD，∠BFC=∠BAD=2∠DFC 求证：（1）CD⊥DF；‎ ‎（2）BC=2CD ‎∴CD⊥DF ‎20、（2009年重庆市江津区）如图，在△ABE中，AB＝AE,AD＝AC,∠BAD＝∠EAC, BC、DE交于点O.‎ 求证：(1) △ABC≌△AED；‎ ‎ (2) OB＝OE .‎ ‎21、（2009年北京市）已知：如图，在△ABC中，∠ACB=，于点D,点E 在AC上，CE=BC,过E点作AC的垂线，交CD的延长线于点F .求证：AB=FC ‎22、（2009年吉林省）如图，，请你写出图中三对全等三角形，并选取其中一对加以证明．‎ B D C F A　郜 E ‎23．（2009年深圳市）如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G。‎ ‎（1）求证：△ABE≌△CBF；‎ ‎（2）若∠ABE=50º，求∠EGC的大小。‎ ‎25、（2009年长沙）如图，是平行四边形对角线上两点，，求证：．‎D C A B E F ‎26、（2009年莆田）已知：如图在中，过对角线的中点作直线分别交的延长线、的延长线于点 ‎（1）观察图形并找出一对全等三角形：____________________，请加以证明；‎ E B M O D N F C A E B M O D N F C A ‎（2）在（1）中你所找出的一对全等三角形，其中一个三角形可由另一个三角形经过怎样的变换得到？‎ ‎ ‎ ‎27、（2009年莆田）（1）根据下列步骤画图并标明相应的字母:（直接在图１中画图）‎ ‎①以已知线段（图1）为直径画半圆；‎ ‎②在半圆上取不同于点的一点，连接；‎ ‎③过点画交半圆于点 ‎（2）尺规作图：（保留作图痕迹，不要求写作法、证明）‎ 已知：（图2）．‎ 求作：的平分线．‎ 图2‎ O B A B A 图1‎ ‎ ‎ 作射线 A D C B E ‎28、（2009年漳州）如图，在等腰梯形中，为底的中点，连结、．求证：．‎ ‎【．‎ ‎29、（2009年哈尔滨）如图，在⊙O中，D、E分别为半径OA、OB上的点，且AD＝BE．‎ 点C为弧AB上一点，连接CD、CE、CO，∠AOC＝∠BOC．‎ 求证：CD＝CE．‎ ‎30、（2009年牡丹江）已知中，为边的中点，‎ 绕点旋转，它的两边分别交、（或它们的延长线）于、‎ 当绕点旋转到于时（如图1），易证 当绕点旋转到不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，、、又有怎样的数量关系？请写出你的猜想，不需证明．‎ A E C F B D 图1‎ 图3‎ A D F E C B A D B C E 图2‎ F ‎32、（2009年甘肃白银）如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：‎ ‎（1）；（2）．‎ A D O C B ‎33、（2009桂林百色）如图：在等腰梯形ABCD中，AD∥BC，对角线AC、BD相交于O．‎ ‎ （1）图中共有 对全等三角形； ‎ ‎（2）写出你认为全等的一对三角形，并证明． ‎ ‎34、（2009白银市）如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：‎ ‎（1）；（2）．‎ ‎35、(2009宁夏) E C B A D 如图：在中，，是边上的中线，将沿边所在的直线折叠，使点落在点处，得四边形．‎ 求证：．‎ ‎36、（2009东营）已知正方形ABCD中，E为对角线BD 上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．‎ ‎（1）求证：EG=CG；‎ ‎（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由． ‎ ‎（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）‎ D F B A C E 图③‎ F B A D C E G 图②‎ F B A D C E G 图①‎ ‎ ‎ ‎．‎ ‎37、（眉山）在直角梯形ABCD中，AB∥DC，AB⊥BC，∠A＝60°，AB＝2CD，E、F分别为AB、AD的中点，连结EF、EC、BF、CF。。‎ ‎⑴判断四边形AECD的形状（不证明）；‎ ‎⑵在不添加其它条件下，写出图中一对全等的三角形，用符号“≌”表示，并证明。‎ ‎⑶若CD＝2，求四边形BCFE的面积。‎ ‎38、（2009年山西省）在中，将绕点顺时针旋转角得交于点，分别交于两点．‎ ‎（1）如图1，观察并猜想，在旋转过程中，线段与有怎样的数量关系？并证明你的结论；‎ A D B E C F A D B E C F ‎（2）如图2，当时，试判断四边形的形状，并说明理由；‎ ‎（3）在（2）的情况下，求的长．‎ ‎39、（2009年黄石市）如图，在上，．‎ 求证：．‎ A B C F E D ‎40、（2009年郴州市）如图6，在下面的方格图中，将ABC先向右平移四个单位得到AB‎1C1，再将AB‎1C1绕点A1逆时针旋转得到AB‎2C2，请依次作出AB‎1C1和AB‎2C2。‎ 图6‎ ‎【答案】正确作出图形即可，图略．平移（4分）旋转（2分）‎ ‎41、（2009年常德市）如图9，若△ABC和△ADE为等边三角形，M，N分别EB，CD的中点，易证：CD=BE，△AMN是等边三角形．‎ ‎ （1）当把△ADE绕A点旋转到图10的位置时，CD=BE是否仍然成立？若成立请证明，若不成立请说明理由；（4分）‎ ‎ （2）当△ADE绕A点旋转到图11的位置时，△AMN是否还是等边三角形？若是，请给出证明，并求出当 AB=2AD时，△ADE与△ABC及△AMN的面积之比；若不是，请说明理由．（6分）‎ 图9 图10 图11‎ 图8‎ ‎42、（2009年广西钦州）（1）已知：如图1，在矩形ABCD中，AF＝BE．求证：DE＝CF；‎ ‎43、（2009年广西梧州）如图（7），△ABC中，AC的垂直平分线MN交AB于 点D，交AC于点O，CE∥AB交MN于E，连结AE、CD．‎ ‎（1）求证：AD＝CE；‎图（7）‎ ‎（2）填空：四边形ADCE的形状是 ★ ．‎ ‎ ‎ ‎44、(2009年甘肃定西)如图13，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：‎ ‎（1）；（2）．‎ ‎45、（2009年清远）如图，已知正方形，点是上的一点，连结，以为一边，在的上方作正方形，连结．‎ 求证：‎ E B C G D F A 图7‎ ‎46、（2009年衢州）如图，四边形ABCD是矩形，△PBC和△QCD都是等边三角形，且点P在矩形上方，点Q在矩形内．‎ 求证：（1）∠PBA=∠PCQ=30°；（2）PA=PQ．‎ A C B D P Q ‎47、（2009年舟山）如图，四边形ABCD是矩形，△PBC和△QCD都是等边三角形，且点P在矩形上方，点Q在矩形内．‎ 求证：（1）∠PBA=∠PCQ=30°；（2）PA=PQ．‎ A C B D P Q ‎ ‎ A C B D P Q ‎48、（2009河池）如图7，在△中，∠ACB=．‎ ‎ （1）根据要求作图：‎ ‎① 作的平分线交AB于D；‎ ‎② 过D点作DE⊥BC，垂足为E．‎ ‎（2）在（1）的基础上写出一对全等三角形 和一对相似比不为1的相似三角形：‎ ‎△ ≌△ ；△ ∽△ ．‎ 请选择其中一对加以证明．‎ ‎ （2）△BDE≌△CDE ；‎ ‎ ‎ ‎49、（09湖南怀化）如图9，P是∠BAC内的一点，，垂足分别为点 ‎．求证：（1）；‎ ‎（2）点P在∠BAC的角平分线上． ‎ ‎【‎ ‎50、（09湖北宜昌）已知：如图2，在Rt△ABC和Rt△BAD中，AB为斜边，AC=BD，BC，AD相交于点E．‎ ‎(1) 求证：AE=BE；‎ ‎(2) 若∠AEC=45°，AC=1，求CE的长． ‎ 图2‎ ‎51、（09湖北宜昌）已知：如图， AF平分∠BAC，BC⊥AF， 垂足为E，点D与点A关于点E对称，PB分别与线段CF， AF相交于P，M．‎ ‎(1)求证：AB=CD；‎ ‎(2)若∠BAC=2∠MPC，请你判断∠F与∠MCD 的数量关系，并说明理由． ‎ ‎ ‎ ‎ ‎ ‎52、(2009年宁德市)如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．‎ ‎（1）连接GD，求证：△ADG≌△ABE；‎ ‎（2）连接FC，观察并猜测∠FCN的度数，并说明理由；‎ ‎（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变，若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．‎ ‎ ‎ 图（2）‎ M B E A C D F G N N M B E C D F G 图（1）‎ ‎ ‎ ‎54、（2009年山东青岛市）用圆规、直尺作图，不写作法，但要保留作图痕迹．‎ A B C 为美化校园，学校准备在如图所示的三角形（）空地上修建一个面积最大的圆形花坛，请在图中画出这个圆形花坛．‎ 解：‎ 结论：‎ 结论．‎ A D G C B F E 第3题图 ‎55、（2009年山东青岛市）已知：如图，在中，AE是BC边上的高，将沿方向平移，使点E与点C重合，得．‎ ‎（1）求证：；‎ ‎（2）若，当AB与BC满足什么数量关系时，四边形是菱形？证明你的结论．‎ ‎，‎ ‎57、（2009年湖北荆州）如图，D是等边△ABC的边AB上的一动点，以CD为一边向上作等边△EDC，连接 AE，找出图中的一组全等三角形，并说明理由．‎ E D C B A ‎【答案】‎ ‎58、（2009湖北荆州年）把一个正方形分成面积相等的四个三角形的方法有很多，除了可以分成能相互全等的四个三角形外，你还能用三种不同的方法将正方形分成面积相等的四个三角形吗？请分别画出示意图。‎ ‎【‎ ‎【答案】‎ ‎59、（2009年茂名市）如图，方格中有一个请你在方格内，画出满足条件 的并判断与是否一定全等？‎ B A C ‎60、(2009年肇庆市)如图 8，在中，‎ ‎，线段 AB 的垂直平分线交 AB于 D，交 AC 于 E，连接BE． ‎ A E C B D 图8‎ ‎（1）求证：∠CBE=36°； ‎ ‎（2）求证：． ‎ ‎ ‎ ‎61、（2009年崇左）如图，在等腰梯形中，已知，，延长到，使．‎ ‎（1）证明：；‎ D A B E C F ‎（2）如果，求等腰梯形的高的值．‎ ‎62、（2009年佳木斯）如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E.‎ ‎（1）试找出一个与△AED全等的三角形，并加以证明.‎ ‎（2）若AB=8，DE=3，P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，试求PG+PH的值，并说明理由.‎ ‎63、（2009年赤峰市）如图，在四边形ABCD中，AB=BC，BF是∠ABC的平分线，AF∥DC，连接AC、CF，求证：CA是∠DCF的平分线。‎ ‎64、(2009年云南省)如图，在△ABC和△DCB中，AB = DC，AC = DB，AC与DB交于点M．‎ ‎（1）求证：△ABC≌△DCB ；‎ ‎（2）过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断线段BN与CN的数量关系，并证明你的结论．‎ B C A D M N