长沙中考近六年数学考点分析 4页

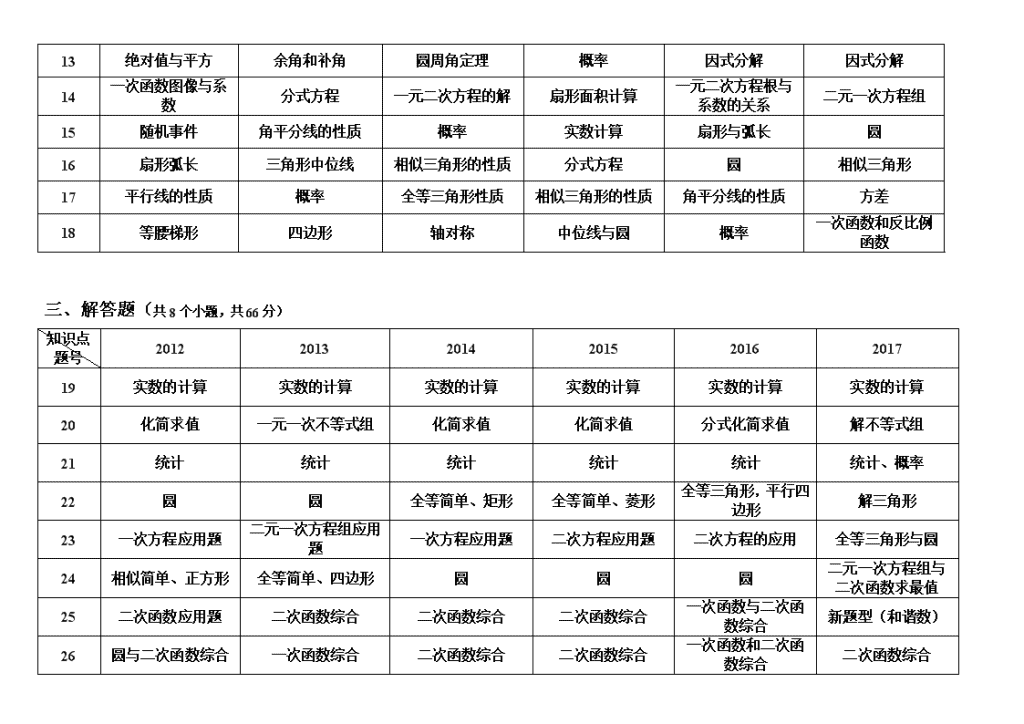
长沙中考近七年考点分析 一、选择题（共10小题，每小题3分，共30分）‎ 知识点 题号 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎1‎ 相反数 无理数 倒数 无理数 有理数 有理数 ‎2‎ 轴对称、中心对称 科学记数法 三视图 幂的运算 科学计数法 整式的运算 ‎3‎ 方差 三角形三边关系 中位数、平均数 科学计数法 幂的运算 科学计数法 ‎4‎ 数轴表示解集 圆与圆的位置关系 平行四边形的性质 轴对称、中心对称 多边形的内角和 轴对称、中心对称 ‎5‎ 四边形的对角线 幂的运算 幂的运算 多边形内角与外角 不等式组的解集 三角形分类 ‎6‎ 补角概念 众数 求线段长 不等式数轴表示解集 三视图 数据的收集、整理 ‎7‎ 一次函数图像应用 角 数轴表示解集 众数 三角形三边关系 三视图 ‎8‎ 三角形中位线 多边形内角与外角 菱形的性质 随机事件 平面直角坐标系 抛物线顶点 ‎9‎ 反比例函数解析式 轴对称、中心对称 中心对称 一次函数图像 余角、补角 平行线性质 ‎10‎ 构成三角形的条件 二次函数图象与系数的关系 二次函数与反比例函数图像 三角形的高 中位数、众数 菱形周长 二、填空题（共8小题，每小题3分，共24分）‎ 知识点 题号 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎11‎ 函数自变量取值范围 实数计算 平行线的性质 三角函数 解直角三角形 一次方程的应用 ‎（选择题）‎ ‎12‎ 三角形的外角 分解因式 二次函数性质 利润问题 二次函数的图像与性质 图形的折叠 ‎（选择题）‎ ‎13‎ 绝对值与平方 余角和补角 圆周角定理 概率 因式分解 因式分解 ‎14‎ 一次函数图像与系数 分式方程 一元二次方程的解 扇形面积计算 一元二次方程根与系数的关系 二元一次方程组 ‎15‎ 随机事件 角平分线的性质 概率 实数计算 扇形与弧长 圆 ‎16‎ 扇形弧长 三角形中位线 相似三角形的性质 分式方程 圆 相似三角形 ‎17‎ 平行线的性质 概率 全等三角形性质 相似三角形的性质 角平分线的性质 方差 ‎18‎ 等腰梯形 四边形 轴对称 中位线与圆 概率 一次函数和反比例函数 三、解答题（共8个小题，共66分）‎ 知识点 题号 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎19‎ 实数的计算 实数的计算 实数的计算 实数的计算 实数的计算 实数的计算 ‎20‎ 化简求值 一元一次不等式组 化简求值 化简求值 分式化简求值 解不等式组 ‎21‎ 统计 统计 统计 统计 统计 统计、概率 ‎22‎ 圆 圆 全等简单、矩形 全等简单、菱形 全等三角形，平行四边形 解三角形 ‎23‎ 一次方程应用题 二元一次方程组应用题 一次方程应用题 二次方程应用题 二次方程的应用 全等三角形与圆 ‎24‎ 相似简单、正方形 全等简单、四边形 圆 圆 圆 二元一次方程组与二次函数求最值 ‎25‎ 二次函数应用题 二次函数综合 二次函数综合 二次函数综合 一次函数与二次函数综合 新题型（和谐数）‎ ‎26‎ 圆与二次函数综合 一次函数综合 二次函数综合 二次函数综合 一次函数和二次函数综合 二次函数综合 ‎2017年长沙市中考题代数部分占65分，其中选择填空题24分，解答题41分；几何部分占41分，其中选择填空题占24，解答题17分；概率统计部分占14分，其中选择填空6分，解答题8分。‎ ‎2018年长沙中考数学分析如下：‎ ‎1、选择题 今年的选择题基本延续了往年的命题风格，比如第1、2、6、8、11等题都能在最近三年的试卷当中找到几乎一样的题型，而且大多数题目都比较简单，但是今年第12题有了明显的难度升级，结合了二次函数与一元一次含参方程无解的知识，题目比较灵活，估计会放倒一大片同学。 2、填空题 填空题整体变化不大，重点考察基础，亮点不多。只要平时基础稳固、复习扎实的孩子，在这个部分应该不会出现太多的问题，大家在这个阶段可以调整心态，轻松去迎接后面的挑战。18题稍微有所变化，历年填空题中涉及到圆的知识主要考察都是垂径定理，用来求弧长或弦长，但今年转换成了求圆心角、圆周角度数，不过难度也不算太大。 3、解答题 19、20题还是原来的配方，还是熟悉的味道，一道综合计算，一道化简求值，这种送分题大家务必要笑纳。21、22题也基本沿用2017年的题型，分别是统计和三角函数。23题和24题在2017年曾经调换了顺序，但在2018年又回归了既定的轨道，23题是一道二元一次方程组的应用，而且难度相比去年有所降低，但是24题的难度有所提升，增加了三角形的外接圆和内切圆的知识考察，这个知识点在近几年中考中都还未曾出现过，因此值得引起注意。 4、压轴题综合比较 中考试卷每一年的25、26题是拉开差距，决定能否上A的关键。25题已经连续5年考察新定义问题，26题的话，几乎每年都是二次函数的代几综合，融合了相似三角形、动点问题、最值问题等知识点。今年这一块有了比较巨大的变化，首先是两题的位置有所调整，25题变成了代几综合题，考察的主要是反比例函数与相似三角形的知识；而26题则是一道新定义的问题，主要融合了平行四边形、二次函数、圆等知识点。此外这两题难度呈现逐年递增的趋势，特别是26题的最后一小问。在17年压轴题中，最后一问求两次最值，计算量就已经不小，今年的最后一小问，由于涉及到根式方程，而且求解过程中还要分类讨论，所以导致计算量巨大，前面题目做得不够快的话，这里估计没有足够的时间完整计算出来。所以对于不少孩子而言，这一问可能就是仅供观赏了。‎ ‎2018年长沙中考数学复习方法总结 导读：中考越来越近了，相信很多学生正在紧锣密鼓地进行备考。数学作为主课，分值比例大，难度也相较较大，想要牢牢地掌握好数学，想必很多同学都开始复习准备了。今天我们为大家分享了关于2018年长沙中考数学复习方法总结，希望能够帮忙大家更好地去复习数学知识点，拿到好成绩。 ‎ ‎　　一是立足基础知识。 ‎ ‎　　复习期间，要重视对基础知识的归纳整理。归纳应按知识模块进行，对概念、定理、公式、法则不仅要熟练掌握、准确叙述，还要学会运用。即使是综合题的求解，也是基础知识、基本方法及数学思维的综合运用，知识和方法的积累是开启难题的钥匙。 ‎ ‎　　二是重视课本习题。 ‎ ‎　　通过分析历年中考数学试题可以看出，用于考查基础知识和基本技能的素材、背景，大都是课本中的例题、习题，或是这些题的变形。因此，对这题要逐一研究，对典型题要亲自演算，重要的步骤、方法可附于题后。 ‎ ‎　　三是掌握解题原理。 ‎ ‎　　在复习中普遍存在重视解题方法，忽视解题原理的倾向。实际上，结果和对错只是考查的一部分，而对知识、能力、思想、方法等方面的考查主要体现在解题步骤和过程中。在专题复习阶段，不仅要掌握解题方法和规律，还要领会其原理。应注意倾听和思考老师对典型题的分析和求解策略，注重通性、通法的运用。及时归纳各种题型，探求不同解法，以便形成能力。 ‎ ‎　　四是落实解题训练。 ‎ ‎　　复习时，一定量的习题训练是必不可少的。通过演练习题，可以加深对基础知识的理解，提高解题能力。单元复习结束或一套试题做完后，都要分析一下，解题中运用了哪些基础知识、基本方法、数学思想，还存在哪些问题，错误的原因是什么，如何改正。要克服不重视解题过程、不愿演算、计算马虎等不良习惯。 ‎ ‎　　五、加强模拟演练。 ‎ ‎　　考前模拟演练既是对复习效果的检查，又可以提升应考信心。要重视模拟过程，淡化模拟分数。应在规定的时间内独立完成试题，批发后及时查找原因。要将模拟考试中发现的问题、做错的题当成一次锻炼和自己的机会。考前发现的问题越多，纠正越及时，提高也就越快，信心就越足。 ‎