2011河南中考数学试题及答案 11页

‎2011年河南省初中学业水平暨高级中等学校招生考试试卷 数 学 注意事项：‎ ‎ 1. 本试卷共8页，三大题，满分120分，考试时间100分钟请用蓝、黑色钢笔或圆珠 笔直接答在试卷上. ‎ ‎2. 答卷前将密封线内的项目填写清楚. ‎ 参考公式：二次函数图象的顶点坐标为.‎ 一、选择题（每小题3分，共18分）‎ 下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内.‎ ‎1. －5的绝对值 【 】‎ ‎（A）5 （B）－5 （C） （D）‎ ‎2. 如图，直线a，b被c所截，a∥b，若∠1=35°，则∠2的大小为 【 】‎ ‎（A）35° （B）145° （C）55° （D）125°‎ ‎3. 下列各式计算正确的是 【 】‎ ‎（A） （B）‎ ‎（C） （D）‎ 的解集在数轴上表示正确的是 【 】‎ x+2＞0，‎ x－1≤2‎ ‎4.不等式 ‎5. 某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验，它们的平均亩产量分别是=610千克，=608千克，亩产量的方差分别是=29. 6， =2. 7. 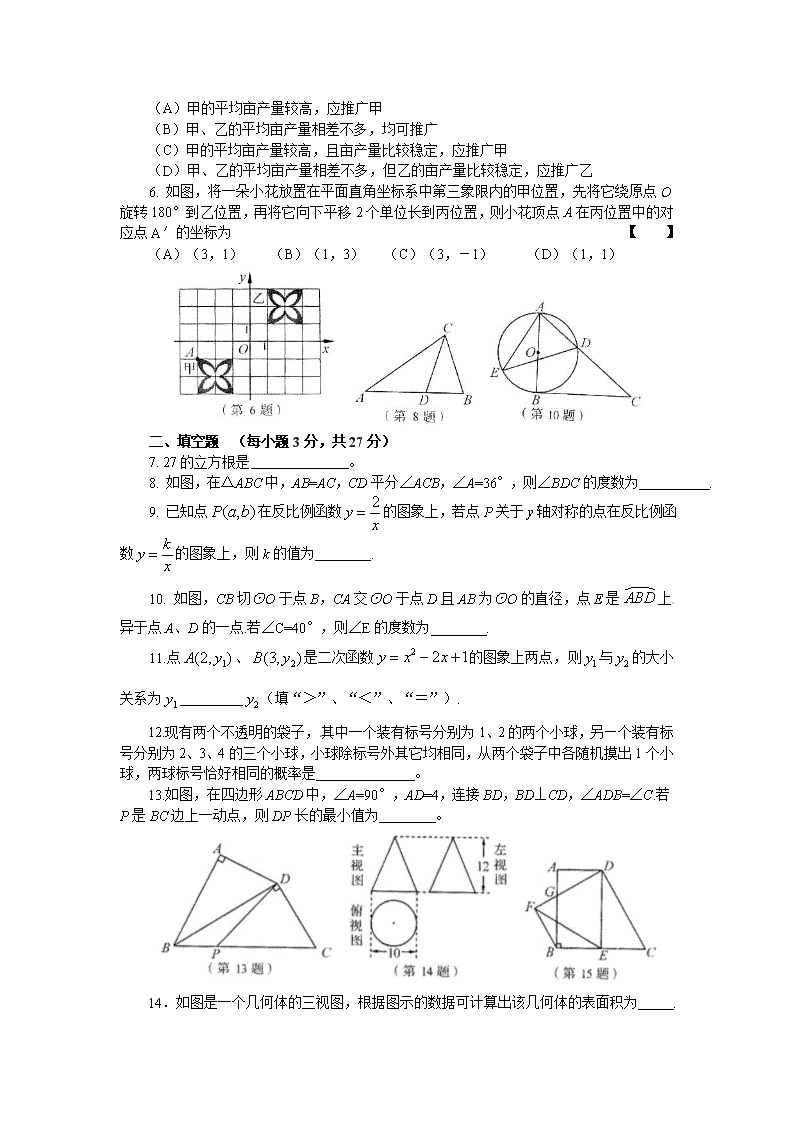则关于两种小麦推广种植的合理决策是 【 】 ‎ ‎（A）甲的平均亩产量较高，应推广甲 ‎（B）甲、乙的平均亩产量相差不多，均可推广 ‎（C）甲的平均亩产量较高，且亩产量比较稳定，应推广甲 ‎（D）甲、乙的平均亩产量相差不多，但乙的亩产量比较稳定，应推广乙 ‎6. 如图，将一朵小花放置在平面直角坐标系中第三象限内的甲位置，先将它绕原点O旋转180°到乙位置，再将它向下平移2个单位长到丙位置，则小花顶点A在丙位置中的对应点A′的坐标为 【 】‎ ‎（A）（3，1） （B）（1，3） （C）（3，－1） （D）（1，1）‎ 二、填空题 （每小题3分，共27分）‎ ‎7. 27的立方根是 。‎ ‎8. 如图，在△ABC中，AB=AC，CD平分∠ACB，∠A=36°，则∠BDC的度数为 .‎ ‎9. 已知点在反比例函数的图象上，若点P关于y轴对称的点在反比例函数的图象上，则k的值为 .‎ ‎10. 如图，CB切⊙O于点B，CA交⊙O于点D且AB为⊙O的直径，点E是上异于点A、D的一点.若∠C=40°，则∠E的度数为 .‎ ‎11.点、是二次函数的图象上两点，则与的大小关系为 （填“＞”、“＜”、“＝”）.‎ ‎12.现有两个不透明的袋子，其中一个装有标号分别为1、2的两个小球，另—个装有标号分别为2、3、4的三个小球，小球除标号外其它均相同，从两个袋子中各随机摸出1个小球，两球标号恰好相同的概率是 。 ‎ ‎13.如图，在四边形ABCD中，∠A=90°，AD=4，连接BD，BD⊥CD，∠ADB=∠C.若P是BC边上一动点，则DP长的最小值为 。‎ ‎14．如图是一个几何体的三视图，根据图示的数据可计算出该几何体的表面积为 .‎ ‎15.如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C=60°，BC=2AD=2，点E是BC边的中点，△DEF是等边三角形，DF交AB于点G，则△BFG的周长为 .‎ 三、解答题 (本大题共8个小题，满分75分)‎ ‎16. （8分）先化简，然后从－2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.‎ ‎17. （9分）如图，在梯形ABCD中，AD∥BC，延长CB到点E，使BE=AD，连接DE交AB于点M.[来源:学#科#网Z#X#X#K]‎ ‎（1）求证：△AMD≌△BME；‎ ‎（2）若N是CD的中点，且MN=5，BE=2，求BC的长.‎ ‎18.(9分)为更好地宣传“开车不喝酒，喝酒不开车”的驾车理念，某市一家报社设计了如右的调查问卷(单选).‎ 在随机调查了奉市全部5 000名司机中的部分司机后，统计整理并制作了如下的统计图：‎ 根据以上信息解答下列问题：‎ ‎(1)补全条形统计图，并计算扇形统计图中m= ；‎ ‎(2)该市支持选项B的司机大约有多少人？‎ ‎(3)若要从该市支持选项B的司机中随机选择100名，给他们发放“请勿酒驾”的提醒标志，则支持该选项的司机小李被选中的概率是多少?‎ ‎19、(9分)如图所示，中原福塔(河南广播电视塔)是世界第—高钢塔．小明所在的课外活动小组在距地面268米高的室外观光层的点D处，测得地面上点B的俯角α为45°，点D到AO的距离DG为10米；从地面上的点B沿BO方向走50米到达点C处，测得塔尖A的仰角β为60°。请你根据以上数据计算塔高AO，并求出计算结果与实际塔高388米之间的误差．(参考数据：≈1.732，≈1.414.结果精确到0.1米)‎ ‎20. （9分）如图，一次函数与反比例函数的图象交于点和，与y轴交于点C.‎ ‎（1）= ，= ；‎ ‎（2）根据函数图象可知，当＞时，x的取值范围是 ；‎ ‎（3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点.设直线 OP与线段AD交于点E，当：=3：1时，求点P的坐标.‎ ‎21. (10分)某旅行杜拟在暑假期间面向学生推出“林州红旗渠一日游”活动，收费标准如下：‎ 人数m ‎0200‎ 收费标准(元/人)‎ ‎90‎ ‎85‎ ‎75‎ 甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．经核算，若两校分别组团共需花费10 800元，若两校联合组团只需花赞18 000元.‎ ‎(1)两所学校报名参加旅游的学生人数之和赳过200人吗?为什么？‎ ‎(2)两所学校报名参加旅游的学生各有多少人?‎ ‎22. （10分）如图，在Rt△ABC中，∠B=90°，BC=5，∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D、E运动的时间是t秒（t＞0）.过点D作DF⊥BC于点F，连接DE、EF.‎ ‎（1）求证：AE=DF；‎ ‎（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由.‎ ‎（3）当t为何值时，△DEF为直角三角形？请说明理由.‎ ‎23. （11分）如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为－8.‎ ‎（1）求该抛物线的解析式； ‎ ‎（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E.‎ ‎①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；‎ ‎②连接PA，以PA为边作图示一侧的正方形APFG.随着点P的运动，正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标.‎ 参考答案及评分标准 说明：‎ ‎1.如果考生的解答与与本参考答案提供的解法不同，可根据提供的解法的评分标准精神进行评分.‎ ‎2.评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定对后面给分的多少，但原则上不超过后继部分应得分数之半.‎ ‎3.评分标准中，如无特殊说明，均为累计给分.‎ ‎4.评分过程中，只给整数分数.‎ 一、选择题（每小题3分，共18分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 答案 A B D B D C 二、填空题（每小题3分，共27分）‎ 题号 ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 ‎3‎ ‎72‎ ‎－2‎ ‎40‎ ‎＜‎ ‎4‎ ‎90π ‎3＋‎ ‎（注：若第8题填为72°，第10题填为40°，不扣分）‎ 三、解答题（本大题共8个小题，满分75分 ）‎ ‎16.原式＝…………………………………………………………3分＝.……………………………………………………………………………5分 x满足－2≤x≤2且为整数，若使分式有意义，x只能取0，－2.……………………7分 当x＝0时，原式＝（或：当x＝－2时，原式＝）. …………………………8分[来源:学科网]‎ ‎17.（1）∵AD∥BC,∴∠A＝MBE，∠ADM＝∠E. …………………………………2分 在△AMD和△BME中，‎ ‎∴△AMD≌△BME. ……………………………………5分 ‎∠A＝∠MBE，‎ AD＝BE，‎ ‎∠ADM＝E，‎ ‎ （2）∵△AMD≌△BME，∴MD＝ME.‎ 又ND＝NC,∴MN＝EC. ……………………………………………………………7分 ‎∴EC＝2MN＝2×5＝10.‎ ‎∴BC＝EC－EB＝10－2＝8. …………………………………………………………9分 ‎18.（1）（C选项的频数为90，正确补全条形统计图）；……………………………2分 ‎20.………………………………………………………………………………………4分 ‎[来源:学科网]‎ ‎（2）支持选项B的人数大约为：5000×23%=1150.……………………………………6分 ‎（3）小李被选中的概率是：………………………………………………9分 ‎19. ∵DE∥BO，α=45°，‎ ‎∴∠DBF=α=45°.‎ ‎∴Rt△DBF中，BF=DF=268.…………………………………………………………2分 ‎∵BC=50，‎ ‎∴CF=BF－BC=268－50=218.‎ 由题意知四边形DFOG是矩形，‎ ‎∴FO=DG=10.‎ ‎∴CO=CF+FO=218+10=228.……………………………………………………………5分 在Rt△ACO中，β=60°，[来源:学科网]‎ ‎∴AO=CO·tan60°≈228×1.732=394.896……………………………………………7分 ‎∴误差为394.896－388=6.896≈6.9（米）.‎ 即计算结果与实际高度的误差约为6.9米.…………………………………………9分 ‎20. （1），16；………………………………………………………………2分 ‎（2）－8＜x＜0或x＞4；…………………………………………………………4分[来源:学科网ZXXK]‎ ‎（3）由（1）知，‎ ‎∴m=4，点C的坐标是（0，2）点A的坐标是（4，4）.‎ ‎∴CO=2，AD=OD=4.………………………………………………………………5分 ‎∴‎ ‎∵‎ ‎∴……………………………………………7分 即OD·DE=4，∴DE=2.‎ ‎∴点E的坐标为（4，2）.‎ 又点E在直线OP上，∴直线OP的解析式是.‎ ‎∴直线OP与的图象在第一象限内的交点P的坐标为（）.‎ ‎…………………………………………………………………………………………9分 ‎21.（1）设两校人数之和为a.‎ 若a＞200，则a=18 000÷75=240.‎ 若100＜a≤200，则，不合题意.‎ 所以这两所学校报名参加旅游的学生人数之和等于240人，超过200人.……3分 ‎（2）设甲学校报名参加旅游的学生有x人，乙学校报名参加旅游的学生有y人，则 ‎①当100＜x≤200时，得 解得………………………………………………………………………………6分 ‎②当x＞200时，得 解得 此解不合题意，舍去.‎ ‎∴甲学校报名参加旅游的学生有160人，乙学校报名参加旅游的学生有80人.‎ ‎………………………………………………………………………………………………10分 ‎22.（1）在△DFC中，∠DFC=90°，∠C=30°，DC=2t，∴DF=t.‎ 又∵AE=t，∴AE=DF.…………………………………………………………………………2分 ‎（2）能.理由如下：‎ ‎∵AB⊥BC，DF⊥BC，∴AE∥DF.‎ 又AE=DF，∴四边形AEFD为平行四边形.…………………………………………………3分 ‎∵AB=BC·tan30°=‎ 若使为菱形，则需 即当时，四边形AEFD为菱形.……………………………………………………5分 ‎（3）①∠EDF=90°时，四边形EBFD为矩形. ‎ 在Rt△AED中，∠ADE=∠C=30°，∴AD=2AE.即10-2t=2t，.………………7分 ‎②∠DEF=90°时，由（2）知EF∥AD，∴∠ADE=∠DEF=90°.‎ ‎∵∠A=90°-∠C=60°，∴AD=AE·cos60°.‎ 即…………………………………………………………………………9分 ‎③∠EFD=90°时，此种情况不存在.‎ 综上所述，当或4时，△DEF为直角三角形.……………………………………10分 ‎23.（1）对于，当y=0，x=2.当x=-8时，y=-.‎ ‎∴A点坐标为（2，0），B点坐标为…………………………………………1分 由抛物线经过A、B两点，得 解得…………………………………………3分 ‎（2）①设直线与y轴交于点M 当x=0时，y=. ∴OM=.‎ ‎∵点A的坐标为（2，0），∴OA=2.∴AM=……………………4分 ‎∵OM：OA：AM=3∶4：5.‎ 由题意得，∠PDE=∠OMA，∠AOM=∠PED=90°，∴△AOM～△PED.‎ ‎∴DE：PE：PD=3∶4：5.…………………………………………………………………5分 ‎∵点P是直线AB上方的抛物线上一动点，‎ ‎∴PD=yP-yD ‎ ‎ ‎=.………………………………………………………………………6分 ‎∴‎ ‎…………………………………………………………………7分 ‎……………………………………8分 ‎②满足题意的点P有三个，分别是 ‎……………………………………………………………11分 ‎【解法提示】‎ 当点G落在y轴上时，由△ACP≌△GOA得PC=AO=2，即，解得，所以 当点F落在y轴上时，同法可得，‎ ‎ （舍去）.‎