- 721.60 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2014年中考数学强化复习(相似三角形)
一、选择题
1、如图1,已知AD与VC相交于点O,AB//CD,如果∠B=40°,
∠D=30°,则∠AOC的大小为( )
A.60° B.70° C.80° D.120°
B
A
C
D
E
A
B
C
D
O
图1
2、如图,已知D、E分别是的AB、 AC边上的点,且 那么等于( )
A.1 : 9 B.1 : 3
C.1 : 8 D.1 : 2
3、如图G是rABC的重心,直线L过A点与BC平行。若直线CG分别与AB、 L交于D、E两点,直线BG与AC交于F点,则rAED的面积:四边形ADGF的面积=?( )
(A) 1:2 (B) 2:1 (C) 2:3 (D) 3:2
A
B
C
D
E
F
A
B
G
C
D
E
F
L
4、 图为rABC与rDEC重迭的情形,其中E在BC上,AC交DE于F点, 且AB // DE。若rABC与rDEC的面积相等,且EF=9,AB=12,则DF=?( )
(A) 3 (B) 7 (C) 12 (D) 15 。
C
A
BA
DA
OA
EA
FA
第18题图
5、如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米, 那么该古城墙的高度是( )
A、6米 B、8米 C、18米 D、24米
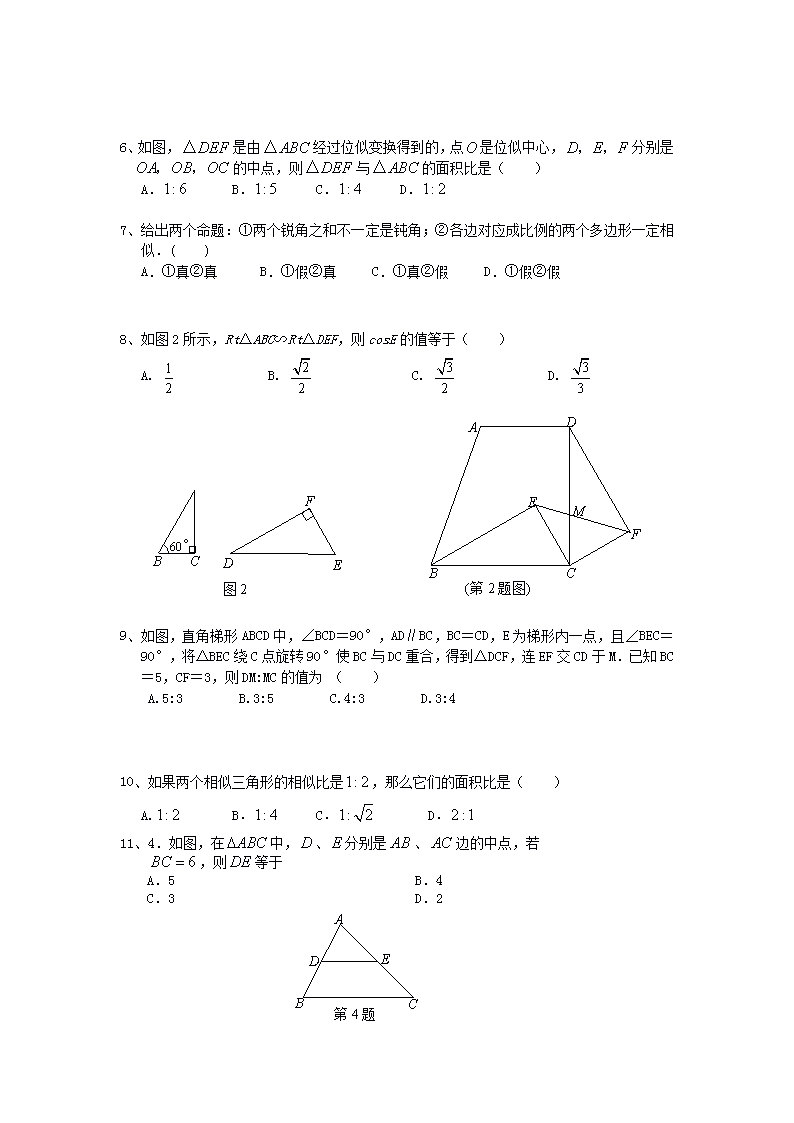
6、如图,是由经过位似变换得到的,点是位似中心,分别是的中点,则与的面积比是( )
A. B. C. D.
7、给出两个命题:①两个锐角之和不一定是钝角;②各边对应成比例的两个多边形一定相似.( )
A.①真②真 B.①假②真 C.①真②假 D.①假②假
8、如图2所示,Rt△ABC∽Rt△DEF,则cosE的值等于( )
A. B. C. D.
A
D
B
C
E
F
M
(第2题图)
F
E
D
B
C
60°
图2
9、如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为 ( )
A.5:3 B.3:5 C.4:3 D.3:4
10、如果两个相似三角形的相似比是,那么它们的面积比是( )
A. B. C. D.
11、4.如图,在中,、分别是、边的中点,若
,则等于
A.5 B.4
第4题
A
B
C
D
E
A
C.3 D.2
12、如图,是由经过位似变换得到的,点是位似中心,分别是的中点,则与的面积比是( ) A. B. C. D.
C
A
BA
DA
OA
EA
FA
第18题图
13、给出两个命题:①两个锐角之和不一定是钝角;②各边对应成比例的两个多边形一定相似.( )
A.①真②真 B.①假②真 C.①真②假 D.①假②假
14、已知,相似比为3,且的周长为18,则的周长为( )
A.2 B.3 C.6 D.54
15、如图,Rt△ABAC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于
D,设BP=x,则PD+PE=( )
A. B. C. D.
16、如图,在Rt△ABC内有边长分别为的三个正方形,则满足的关系式是( )
A、 B、
C、 D、
17、如图,△ABC是等边三角形,被一平行于BC的矩形所截,
AB被截成三等分,则图中阴影部分的面积是△ABC的面积的 ( )
A. B. C. D.
E
H
F
G
C
B
A
((第10题图)
18、如图,在△ABC中,若DE∥BC,=,DE=4cm,则BC的长为( )
A.8cm B.12cm C.11cm D.10cm
19、下列四个三角形,与左图中的三角形相似的是( )
(第7题)
A.
B.
C.
D.
20、若△ABC∽△DEF,△ABC与△DEF的相似比为2︰3,则S△ABC︰S△DEF为()
A、2∶3 B、4∶9 C、∶ D、3∶2
21、在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为( )
A、4.8米 B、6.4米 C、9.6米 D、10米
22、小刚身高1.7m,测得他站立在阳关下的影子长为0.85m。紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起手臂超出头顶
A.0.5m B.0.55m C.0.6m D.2.2m
33、如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中相似的是( )
A.
B.
C.
D.
A
B
C
二、填空题
1、如图,两点分别在的边上,与不平行,当满足 条件(写出一个即可)时,.
E
C
D
A
F
B
图5
2、如果两个相似三角形的相似比是,那么这两个三角形面积的比是 .
3、如图5,平行四边形中,是边上的点,交于点,如果,
那么 .
4、在比例尺为1︰2000的地图上测得AB两地间的图上距离为5cm,则AB
两地间的实际距离为 m.
5、在Rt△ABC中,∠C为直角,CD⊥AB于点D,
BC=3,AB=5,写出其中的一对相似三角形是 和 ;
并写出它的面积比 .
6、已知∠A=40°,则∠A的余角等于=________度.
(第16题图)
O
A1
A2
A3
A4
A
B
B1
B2
B3
1
4
7、如图,点在射线上,点在射线上,且,.若,的面积分别为1,4,则图中三个阴影三角形面积之和
为 .
8、两个相似三角形周长的比为2:3,则其对应的面积比为___________.
图8
9、两个相似三角形的面积比S1:S2与它们对应高之比h1:h2之间的关系为 .
10、如图8,D、E分别是的边AB、AC上的点,则使∽的条件是 .
11、如图4,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=
(第12题)
A
B
C
E
D
12、如图,在中,分别是的中点,若,则的长是 .
图3
13、如图3,要测量A、B两点间距离,在O点打桩,取OA的中点 C,OB的中点D,测得CD=30米,则AB=______米.
14、如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则光线从A点到B点经过的路线的长度为 .(精确到0.01)
15、如图,中,,两点分别在边上,且与不平行.请填上一个你认为合适的条件: ,使.
(不再添加其他的字母和线段;只填一个条件,多填不给分!)
16、如图5,若△ABC∽△DEF,则∠D的度数为_____________..
E
C
D
A
F
B
17、如果两个相似三角形的相似比是,那么这两个三角形面积的比是 .
18、如图,平行四边形中,是边上的点,交于点,如果,那么 .
三、解答题
1、如图5,在△ABC中,BC>AC, 点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
2、如图,在中,。
(1)在图中作出的内角平分线AD。(要求:尺规作图,保留作图痕迹,不写证明)
(2)在已作出的图形中,写出一对相似三角形,并说明理由。
提示:(1)如图,AD即为所求。
3、(本题6分)如图,点D,E在BC上,且FD∥AB,FE∥AC。
F
E
D
C
B
A
求证:△ABC∽△FDE.
4、(本小题满分10分)
如图:在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.
(1) 证明:∠CAE=∠CBF;
(2) 证明:AE=BF;
(3) 以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记△ABC和△ABG的面积分别为S△ABC和S△ABG,如果存在点P,能使得S△ABC=S△ABG,求∠C的取之范围。
F
C
A
B
P
E
H
5、如图,在直角△ABC内,以A为一个顶点作正方形ADEF,使得点E落在BC边上.
(1) 用尺规作图,作出D、E、F中的任意一点 (保留作图痕迹,不写作法和证明. 另外两点不需要用尺规作图确定,作草图即可);
(2) 若AB = 6,AC = 2,求正方形ADEF的边长.
A
B
C
第21题图
6、阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺、标杆、一副三角尺、小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.
(1)所需的测量工具是: ;
(2)请在下图中画出测量示意图;
(3)设树高的长度为,请用所测数据(用小写字母表示)求出.
第20题图
7、如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
(1)求证:AB·AF=CB·CD
(2)已知AB=15cm,BC=9cm,P是射线DE上的动点.设DP=xcm(x>0),四边形BCDP的面积为ycm2.
①求y关于x的函数关系式;
②当x为何值时,△PBC的周长最小,并求出此时y的值.
8、如图10,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.
求证:(1);
(2)
9、△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
Ⅰ.证明:△BDG≌△CEF;
A
B
C
D
E
F
G
图 (1)
Ⅱ. 探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答. 如果两题都解,只以Ⅱa的解答记分.
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.
设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
A
B
C
D
E
F
G
图 (2)
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
A
B
C
D
E
F
G
图 (3)
G′
F′
E′
D′
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.
10、如图11,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图12).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD+CE=DE.
G
y
x
O
F
E
D
C
B
A
(4)在旋转过程中,(3)中的等量关系BD+CE=DE是否始终成立,若成立,请证明,若不成立,请说明理由.
G
F
E
D
C
B
A
11、如图,在中,,,,分别是边的中点,点从点出发沿方向运动,过点作于,过点作交于,当点与点重合时,点停止运动.设,.
(1)求点到的距离的长;
(2)求关于的函数关系式(不要求写出自变量的取值范围);
A
B
C
D
E
R
P
H
Q
(第1题图)
(3)是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由.
12、在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
A
B
C
M
N
P
图 1
O
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
13、如图,四边形和四边形都是平行四边形,点为的中点,分别交于点.
第20题图
A
B
C
D
E
P
O
R
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求.
第21题图
14、如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,。
⑴求证:△ABF∽△CEB;
⑵若△DEF的面积为2,求□ABCD的面积。
15、为了加强视力保护意识,小明想在长为3.2米,宽为4.3米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计方案新颖,构思巧妙.
(1)甲生的方案:如图1,将视力表挂在墙和墙的夹角处,被测试人站立在
对角线上,问:甲生的设计方案是否可行?请说明理由.
(2)乙生的方案:如图2,将视力表挂在墙上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙 米处.
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距 为3m的小视
H
H
(图1)
(图2)
(图3)
(第22题)
3.5㎝
A
C
F
3m
B
5m
D
力表.如果大视力表中“”的长是3.5cm,那么小视力表中相应“”的长是多少cm?
16、如图,E是□ABCD的边BA延长线上一点,连接EC,交AD于F.在不添加辅助线的情况下,请找出图中的一对相似三角形,并说明理由.
A F D
B C
E
17、如图,在平面直角坐标系中,点,点分别在轴,轴的正半轴上,且满足.
(1)求点,点的坐标.
(2)若点从点出发,以每秒1个单位的速度沿射线运动,连结.设的面积为,点的运动时间为秒,求与的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点,使以点为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.
18、在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
A
B
C
M
N
P
图 3
O
A
B
C
M
N
D
图 2
O
A
B
C
M
N
P
图 1
O
19、将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图9,AC= ,BD= ;四边形ABCD是 梯形.
(2)请写出图9中所有的相似三角形(不含全等三角形).
(3)如图10,若以AB所在直线为轴,过点A垂直于AB的直线为轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
D
C
B
A
E
图9
E
D
C
H
F
G
B
A
P
y
x
图10
10
.
20、(本题满分13分)
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
(第21题)
21、本题满分8分.
如图8,四边形是平行四边形.O是对角线的中点,过点的直线分别交AB、DC于点、,与CB、AD的延长线分别交于点G、H.
(1)写出图中不全等的两个相似三角形(不要求证明);
图8
(2)除AB=CD,AD=BC,OA=OC这三对相等的线段外,图中还有多对相等的线段,请选出其中一对加以证明.
22、本题满分8分.
如图10所示,E是正方形ABCD的边AB上的动点, EF⊥DE交BC于点F.
(1)求证: ADE∽BEF;
(2)设正方形的边长为4, AE=,BF=.当取什么值时, 有最大值?并求出这个最大值.
23.如图,在△ABD和△ACE中,AB=AD,AC=AE,∠BAD=∠CAE,连结BC、DE相交于点F,BC与AD相交于点G.
(1)试判断线段BC、DE的数量关系,并说明理由
(2)如果∠ABC=∠CBD,那么线段FD是线段FG和FB的比例中项吗?为什么?
24、如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°
【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q
【探究一】在旋转过程中,
(1)如图2,当时,EP与EQ满足怎样的数量关系?并给出证明.
(2)如图3,当时EP与EQ满足怎样的数量关系?,并说明理由.
(3)根据你对(1)、(2)的探究结果,试写出当时,EP与EQ满足的数量关系式为_________,其中的取值范围是_______(直接写出结论,不必证明)
【探究二】若,AC=30cm,连续PQ,设△EPQ的面积为S(cm2),在旋转过程中:
(1)S是否存在最大值或最小值?若存在,求出最大值或最小值,若不存在,说明理由.
(2)随着S取不同的值,对应△EPQ的个数有哪些变化?不出相应S值的取值范围.
(图1) (图2) (图3)
25、(14分)如图(1)所示,一张平行四边形纸片ABCD,AB=10,AD=6,BD=8,沿对角线BD把这张纸片剪成△AB1D1和△CB2D2两个三角形(如图(2)所示),将△AB1D1沿直线AB1方向移动(点B2始终在AB1上,AB1与CD2始终保持平行),当点A与B2重合时停止平移,在平移过程中,AD1与B2D2交于点E,B2C与B1D1交于点F,
(1)当△AB1D1平移到图(3)的位置时,试判断四边形B2FD1E是什么四边形?并证明你的结论;
(2)设平移距离B2B1为x,四边形B2FD1E的面积为y,求y与x的函数关系式;并求出四边形B2FD1E的面积的最大值;
(3)连结B1C(请在图(3)中画出)。当平移距离B2B1的值是多少时,△ B1B2F与△ B1CF相似?
A
B
C
D
A
C
B1(B2)
D1(D2)
A
C
E
F
B2
B1
D1
D2
参考答案
一、 选择题
1、B 2、B 3、D 4、B 5、B 6、C 7、C 8、A 9、C 10、B
11、C 12、C 13、C 14、C 15、A 16、A 17、C
18、B 19、B 20、B 21、C 22、A 23、B
二、填空题
1、∠ADE=∠ACB(或∠AED=∠ABC或错误!不能通过编辑域代码创建对象。)
2、 3、 4、100 5、 6、50 7、10.5 8、4:9 9、
10、,或,或
11、4 12、10 13、60 14、6.71 15、 16、30° 17、
18、
三、解答题
1、(1)证明:
,
∴ .
又∵ ,
∴ CF是△ACD的中线,
∴ 点F是AD的中点.
∵ 点E是AB的中点,
∴ EF∥BD,
即 EF∥BC.
(2)解:由(1)知,EF∥BD,
∴ △AEF∽△ABD ,
∴ .
又∵ ,
,
∴ ,
∴ ,
∴ 的面积为8.
2、(2),理由如下:
AD平分则,
又,故。
3、证明:略
4、(1)∵△ABC为等腰三角形
∴AC=BC ∠CAB=∠CBA
又∵CH为底边上的高,P为高线上的点
∴PA=PB
∴∠PAB=∠PBA
∵∠CAE=∠CAB-∠PAB
∠CBF=∠CBA-∠PBA
∴∠CAE=∠CBF
(2)∵AC=BC
∠CAE=∠CBF
∠ACE=∠BCF
∴△ACE~△BCF(AAS)
∴AE=BF
(3)若存在点P能使S△ABC=S△ABG,因为AE=BF,所以△ABG也是一个等腰三角形,这两个三角形面积相等,底边也相同,所以高也相等,进而可以说明△ABC~△ABG,则对应边AC=AE,∠ACE=∠AEC,所以0°≤∠C<90°
5、解:⑴ 作图:作∠BAC的平分线交线段BC于E; ………………4分
A
B
C
第21题图
D
E
F
(痕迹清晰、准确,本步骤给满分4分,否则酌情扣1至4分;另外两点及边作的是否准确,不扣分)
⑵ 如图,∵ 四边形ADEF是正方形,
∴ EF∥AB,AD = DE = EF = FA. 5分
∴ △CFE ∽△CAB.
∴ .………………6分
∵ AC = 2 ,AB = 6,
设AD = DE = EF = FA = x,
∴ . …………………7分
∴ x=.即正方形ADEF的边长为. ……………8分
C
D
E
F
B
A
(第20题答案图)
(本题可以先作图后计算,也可以先计算后作图;未求出AD或AF的值用作中垂线的方法找到D点或F点,给2分)
6、解:(1)皮尺、标杆.
(2)测量示意图如右图所示.
(3)如图,测得标杆,
树和标杆的影长分别为,.
,
.
.
.
7、(1)证明:∵AD=CD,DE⊥AC,∴DE垂直平分AC
∴AF=CF,∠DFA=DFC=90°,∠DAF=∠DCF.
∵∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°,∴∠DCF=∠DAF=∠B
在Rt△DCF和Rt△ABC中,∠DFC=∠ACB=90°,∠DCF=∠B
∴△DCF∽△ABC
∴,即.∴AB·AF=CB·CD
(2)解:①∵AB=15,BC=9,∠ACB=90°,
∴AC===12,∴CF=AF=6
∴×6=3x+27(x>0)
②∵BC=9(定值),∴△PBC的周长最小,就是PB+PC最小.由(1)可知,点C关于直线DE的对称点是点A,∴PB+PC=PB+PA,故只要求PB+PA最小.
显然当P、A、B三点共线时PB+PA最小.此时DP=DE,PB+PA=AB.
由(1),∠ADF=∠FAE,∠DFA=∠ACB=90°,地△DAF∽△ABC.
EF∥BC,得AE=BE=AB=,EF=.
∴AF∶BC=AD∶AB,即6∶9=AD∶15.∴AD=10.
Rt△ADF中,AD=10,AF=6,∴DF=8.
∴DE=DF+FE=8+=.
∴当x=时,△PBC的周长最小,此时y=
8、证明:(1)四边形和四边形都是正方形
(2)由(1)得
∴AMN∽CDN
9、Ⅰ.证明:∵DEFG为正方形,
∴GD=FE,∠GDB=∠FEC=90°
∵△ABC是等边三角形,∴∠B=∠C=60°
∴△BDG≌△CEF(AAS)
A
B
C
D
E
F
G
解图 (2)
H
Ⅱa.解法一:设正方形的边长为x,作△ABC的高AH,
求得
由△AGF∽△ABC得:
解之得:(或)
解法二:设正方形的边长为x,则
在Rt△BDG中,tan∠B=,
∴
解之得:(或)
解法三:设正方形的边长为x,
则
A
B
C
D
E
F
G
解图 (3)
G’
F’
E’
D’
由勾股定理得:
解之得:
Ⅱb.解: 正确
由已知可知,四边形GDEF为矩形
∵FE∥F’E’ ,
∴,
同理,
∴
又∵F’E’=F’G’,
∴FE=FG
因此,矩形GDEF为正方形
10、解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA
∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°
∴∠BAE=∠CDA
又∠B=∠C=45°
∴∆ABE∽∆DCA
(2)∵∆ABE∽∆DCA
∴
由依题意可知CA=BA=
∴
∴m=
自变量n的取值范围为1