上海市杨浦区中考二模数学试题及答案 8页

‎2014年杨浦区初三模拟测试 数 学 试 卷 ‎ （满分150分，考试时间100分钟） 2014.5.8‎ 考生注意：‎ ‎1．本试卷含三个大题，共25题；‎ ‎2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；‎ ‎3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】‎ ‎1．点A是数轴上的任意一点，则下列说法正确的是（ ▲ ）‎ ‎（A）点A表示的数一定是整数； （B）点A表示的数一定是分数； ‎ ‎（C）点A表示的数一定是有理数； （D）点A表示的数可能是无理数．‎ ‎2．下列关于x的方程一定有实数解的是（ ▲ ）‎ ‎(第3题图)‎ ‎（A）； （B）；‎ ‎（C）； （D）．‎ ‎3．某学校为了了解九年级学生体能情况，随机选取30名 学生测试一分钟仰卧起坐次数，并绘制了直方图（如图），‎ 学生仰卧起坐次数在25～30之间的频率为（ ▲ ）‎ ‎（A）0.1； （B）0.4； ‎ ‎（C）0.33； （D）0.17．‎ ‎4．将抛物线平移到抛物线的位置，以下描述正确的是（ ▲ ）‎ ‎（A）向左平移1个单位，向上平移1个单位；（B）向右平移1个单位，向上平移1个单位；（C）向左平移1个单位，向下平移1个单位；（D）向右平移1个单位，向下平移1个单位．‎ ‎5．下列图形既是中心对称又是轴对称的是（ ▲ ）‎ ‎（A）菱形； （B）梯形； （C）正三角形； （D）正五边形．‎ ‎6．下列条件一定能推得△ABC与△DEF全等的是（ ▲ ）‎ ‎（A）在△ABC和△DEF中，∠A=∠B，∠D=∠E，AB=DE；‎ ‎（B）在△ABC和△DEF中，AB=AC，∠A=∠F， FD=FE；[来源:www.shulihua.net]‎ ‎（C）在△ABC和△DEF中，；‎ ‎（D）在△ABC和△DEF中，．‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎【请将结果直接填入答题纸的相应位置上】‎ ‎7．计算：= ▲ ．‎ ‎8．方程的解是 ▲ ．‎ ‎0‎ ‎1‎ x y ‎(第10题图)‎ ‎9．如果反比例函数的图像在第二、四象限，那么的取值范围是 ▲ ．‎ ‎10．函数的大致图像如图所示，则当时，的取值 范围是 ▲ ．‎ ‎11．黄老师在数学课上给出了6道习题，要求每位同学独立完成。‎ 现将答对的题目数与相应的人数列表如下：‎ 答对题目数 ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 相应的人数 ‎1‎ ‎2‎ ‎6‎ ‎8‎ ‎3‎ 则这些同学平均答对 ▲ 道题．‎ ‎12．从分别标有1、2、3、4的四张卡片中，一次同时抽2张，其中和为奇数的概率是 ▲ ．‎ ‎13．在Rt△ABC中，∠C=90°，点D为AB边上中点，如果，那么 ‎ ▲ (用表示)．‎ ‎14．如果人在一斜坡坡面上前行100米时，恰好在铅垂方向上上升了10米，那么该斜坡的坡度是 ▲ ．‎ ‎15．如图，△ABC中，∠A=80°，∠B=40°，BC的垂直平分线交AB 于点D，联结DC。如果AD=2，BD=6，那么△ADC的周长为 ▲ ．‎ ‎16．如图，在Rt△ABC中，∠A=90°，∠B=30°，BC=10，以A为圆心画圆，如果⊙A与直线BC相切，那么⊙A的半径长为 ▲ ．‎ ‎17．如果将点（-b，-a）称为点（a，b）的“反称点”，那么点（a，b）也是点（-b，-a）的“反称点”，此时，称点（a，b）和点（-b，-a）是互为“反称点”。容易发现，互为“反称点”的两点有时是重合的，例如（0，0）的“反称点”还是（0，0）。请再写出一个这样的点： ▲ ．‎ ‎18．如图，在菱形ABCD中，AB=a，∠ABC=。将菱形ABCD绕点B顺时针旋转（旋转角小于90°），点A、C、D分别落在A’、C’、D’处，当 A’C’⊥BC时A’D= ▲ （用含a和的代数式表示）．‎ A B C D ‎（第18题图）‎ ‎（第15题图）‎ A B C D A B C ‎（第16题图）‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ 先化简，再求值：，．[来源:www.shulihua.net]‎ ‎[来源:www.shulihua.netwww.shulihua.net]‎ ‎20．（本题满分10分）‎ 解不等式组：且写出使不等式组成立的所有整数。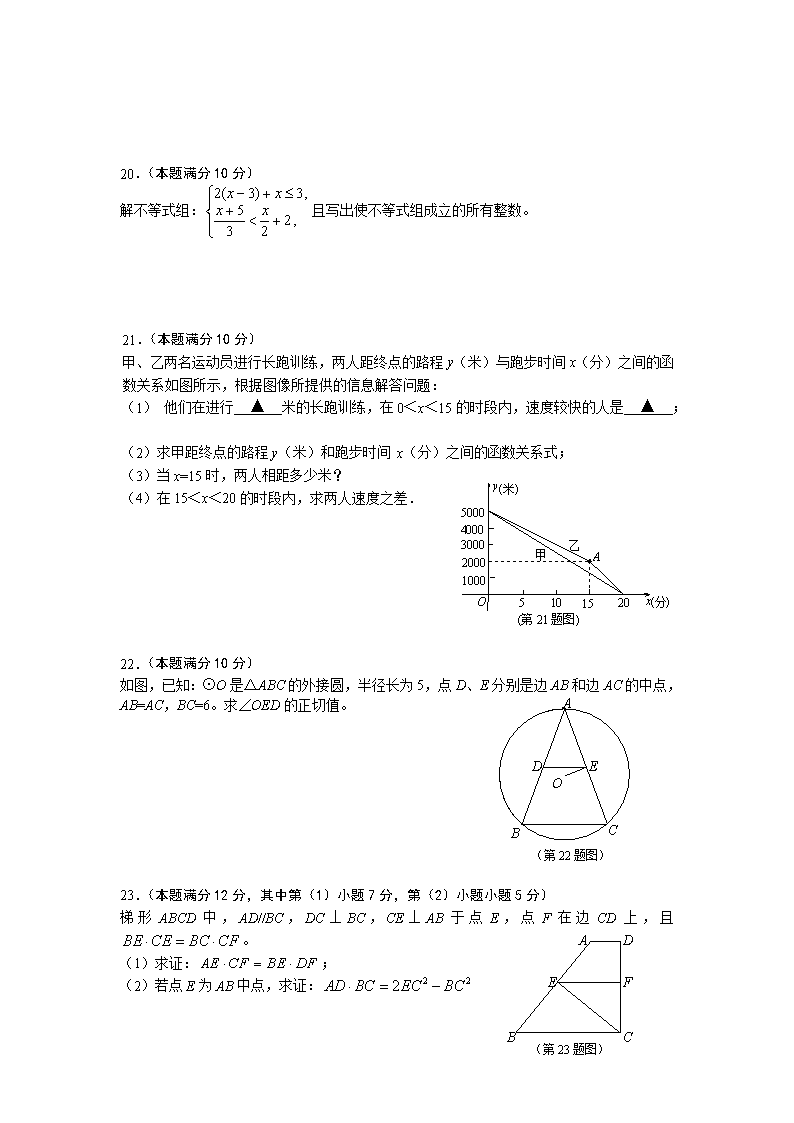‎ ‎21．（本题满分10分）‎ 甲、乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x（分）之间的函数关系如图所示，根据图像所提供的信息解答问题：‎ ‎（1） 他们在进行 ▲ 米的长跑训练，在0＜x＜15的时段内，速度较快的人是 ▲ ；[来源:www.shulihua.net ‎（2）求甲距终点的路程y（米）和跑步时间 x（分）之间的函数关系式；‎ ‎(第21题图)‎ ‎（3）当x=15时，两人相距多少米？‎ ‎（4）在15＜x＜20的时段内，求两人速度之差．‎ ‎22．（本题满分10分）‎ A B C D E O ‎（第22题图）‎ 如图，已知：⊙O是△ABC的外接圆，半径长为5，点D、E分别是边AB和边AC的中点，AB=AC，BC=6。求∠OED的正切值。‎ ‎23．（本题满分12分，其中第（1）小题7分，第（2）小题小题5分）‎ A B C D E F ‎（第23题图）‎ 梯形ABCD中，AD//BC，DC⊥BC，CE⊥AB于点E，点F在边CD上，且。‎ ‎（1）求证：；‎ ‎（2）若点E为AB中点，求证：‎ ‎24．（本题满分12分，其中第（1）小题3分，第（2）小题5分，第（3）小题4分）‎ x y O ‎（第24题图）‎ 直线过点A（１，－４），与x轴交于点B，与y轴交于点D，以点A为顶点的抛物线经过点B，且交y轴于点C。‎ ‎（1）求抛物线的表达式；‎ ‎（2）如果点P在x轴上，且△ACD与△PBC相似，求点P的坐标；‎ ‎（3）如果直线l与直线关于直线BC对称，‎ 求直线l的表达式。‎ ‎[来源:数理化网]‎ ‎25．（本题满分14分，其中第（1）小题4分，第（2）、（3）小题各5分）‎ 已知梯形ABCD中，AD//BC，AD=1，BC=2，sinB=。过点C在∠BCD的内部作射线交射 线BA于点E，使得∠DCE＝∠B。‎ ‎（1）如图1，当ABCD为等腰梯形时，求AB的长；‎ ‎（2）当点E与点A重合时（如图2），求AB的长；‎ A B C D ‎（图1）‎ B C D ‎(E)‎ ‎（图2）‎ A ‎（第25题图）‎ ‎（3）当△BCE为直角三角形时，求AB的长。‎ ‎(备用图)‎ B C ‎2014年杨浦区初三模拟测试数学试卷答案与评分标准2014.5.8‎ 一、 选择题 ‎1、D；2、C；3、B；4、C；5、A；6、D；‎ 二、 填空题 ‎7、；8、；9、；10、；11、4.5；12、；13、；14、；15、14；16、；17、（3，-3）；18、；‎ 三、 解答题 ‎19、解:原式=-----------------------------------------（6分）‎ ‎==--------------------------------------------------------（2分）‎ 当时， 原式=-------------------------------------（2分）‎ ‎20、解：----------------------------------------------------------------------（2分）‎ ‎-----------------------------------------------------------------------------------（2分）‎ 得---------------------------------------------------------------------------------（2分）‎ ‎∴不等式组的解集是－2＜x≤3．-----------------------------------------------------（2分）‎ 使不等式组成立的所有整数是-1、0、1、2、3．----------------------------------（2分）‎ ‎21、解：（1）5000-------------------------------------------------------------------------------------（1分）‎ 甲 -------------------------------------------------------------------------------------（1分）‎ ‎（2）设所求直线的解析式为：y =kx+5000，-----------------------------------------（1分）‎ 由图象可知：当x=20时，y=0，‎ ‎∴0=20k+5000，解得k= -250. --------------------------------------------------（1分）‎ 即y = -250x+5000 ------------------------------------------------------------------（1分）‎ ‎（3）当x=15时，y = -250x+5000= -250×15+5000=5000-3750=1250. ------------（2分）‎ 两人相距： 2000-1250=750（米）. ----------------------------------------------（1分）‎ ‎(4) 两人速度之差:750÷(20-15)=150（米/分） ---------------------------------（2分）‎ ‎22、解：联结AO并延长交BC于点H，联结OC，‎ ‎∵AB=AC，∴，‎ ‎∵O为圆心，∴AH⊥BC，BH=HC，---------------------------------------------------------------(2分)‎ ‎∴HC=3，∵半径OC=5，∴OH=4，AH=9，------------------------------------------（2分）‎ ‎∴在Rt△AHC中，tan∠HAC=，即tan∠OAE=,----------------（2分）‎ ‎∵D、E分别是边AB和边AC的中点，∴DE//BC，∴AH⊥DE，∴∠OAE+∠AED=90°，‎ ‎∵E是边AC的中点，O为圆心，∴OE⊥AC，∴∠AED+∠OED=90°，‎ ‎∴∠OAE=∠OED，--------------------------------------------------------------------------（2分）‎ ‎∴tan∠OED= tan∠OAE=.----------------------------------------------------------------（2分）‎ ‎23、证明：（1）∵CE⊥AB，∴∠B+∠BCE=90°，‎ ‎∵DC⊥BC，∴∠DCE+∠BCE=90°，∴∠B=∠DCE，-----------（2分）‎ ‎∵，∴，∴△BCE∽△CEF，------(2分)‎ ‎∴∠BCE=∠CEF，------------------------------------------------------------(1分)‎ ‎∴EF//BC，----------------------------------------------------------------------(1分)‎ ‎∴，即。--------------------------------(1分)‎ ‎（2）在梯形中，∵EF//BC，E为AB中点，∴，--------（1分）‎ ‎ ∵△BCE∽△CEF，∴，即，-----------------（1分）‎ ‎ ∴，---------------------------------------------------（1分）‎ 整理得--------------------------------------------------（2分）‎ ‎24、解：（1）∵过点A（１，－４），∴，∴k=2，∴B（3,0），（1分）‎ ‎ ∵以点A为顶点的抛物线经过点B，∴设解析式为，----（1分）‎ ‎ 且，∴，∴抛物线的表达式为。----（1分）‎ ‎（2）∵k=2，∴即为，∴D（0，-6），‎ ‎∵抛物线与y轴交于点C，∴C（0，-3），‎ ‎∵A（１，－４），∴∠DCA＝45°，且AC=，CD=3，‎ ‎ ∵B（3,0），C（0，-3），∴∠OCB＝45°，∴∠DCA＝∠OCB-------------------（1分）‎ ‎∵△ACD与△PBC相似，且点P在x轴上，‎ ‎∴点P在B点的左侧，且或，即或，‎ ‎∴BP=2或9， --------------------------------------------------------------------------（1分，1分）‎ ‎∴点P（1,0）或（-6,0）。--------------------------------------------------------------------（2分）‎ ‎（3）过点D作DH⊥BC并延长DH到点M，使HM=HD，联结CM、BM，----------（1分）‎ ‎∴直线BM即为直线l，且CM=CD，∠MCH＝∠DCH， ‎ ‎∵C（0，-3），D（0，-6），∴CM=CD=3，‎ ‎∵B（3,0），C（0，-3），∴∠OCB＝45°，∴∠DCH＝∠OCB＝45°，‎ ‎∴∠MCH＝45°，∴∠MCD＝90°，即MC⊥y轴，∵MC=CD=3，‎ ‎∴M（-3，-3）,----------------------------------------------------------------------------（1分）‎ ‎ 设直线l的解析式为，则，--------------（2分）‎ ‎∴直线l的解析式为。‎ ‎25、解：（1）作AM//DC交BC于点M，‎ ‎∵AD//BC，∴ AMCD为平行四边形，------------------------------------------------------（1分）‎ ‎∴AM=DC，MC=AD=1，∴BM=BC-MC=2-1=1，‎ 作AH⊥BC于点H，‎ ‎∵ABCD为等腰梯形，∴AB=DC，∴AB=AM，∴BH=HM=------------（1分）‎ 在直角三角形ABH中，∵sinB=，∴cosB=，∴，∴。-----（2分）‎ ‎（2）∵AD//BC，∴∠DAC＝∠ACB，又∵∠DCE＝∠B，∴△ADC∽△CAB，----(1分)‎ ‎∴，∴,------------------------------------------------------（2分）‎ 作AF⊥BC于点F，设AB=x，∵sinB=，∴，∴，‎ 在直角三角形AFC中，，即，‎ ‎∴，-----------------------------------------------------------------------------------（2分）‎ 即当点A与点E重合时，或。‎ ‎（3）∵△BCE为直角三角形，∴BE⊥CE或BC⊥CE，‎ 情况一，当BE⊥CE时，如图1，‎ ‎∵∠DCE＝∠B，∠B+∠BCE=90°，∴∠DCE+∠BCE=90°，‎ 作AK⊥BC，设AB=x，∴KC=AD=1，，‎ ‎∵BC=2，∴，∴；-------------------------------------------------------（2分）‎ 情况二，当BC⊥CE时，如图2，‎ 延长DA交CE的延长线于点P，设，则，‎ 在直角三角形BCE中，∵BC=2，sinB=，∴，‎ ‎∵AD//BC，BC⊥CE，∴AD⊥EC，又∵∠DCE＝∠B，∴△PDC∽△CEB，‎ ‎∴，即，∴，∴，‎ A B C D E ‎（图1）‎ A B C D E P ‎（图2）‎ ‎∴-------------------------------------------------（3分）‎ ‎∴当△BCE为直角三角形时，或 ‎