中考数学压轴题100题精6180题及答案 43页

‎2010中考数学压轴题100题精选（61-80题）‎ ‎【061】如图已知直线L：，它与x轴、y轴的交点分别为A、B两点。‎ ‎（1）求点A、点B的坐标。‎ ‎（2）设F为x轴上一动点，用尺规作图作出⊙P，使⊙P经过点B且与x轴相切于点F（不写作法，保留作图痕迹）。‎ ‎（3）设92）中所作的⊙P的圆心坐标为P（x，y），求y关于x的函数关系式。‎ ‎（4）是否存在这样的⊙P，既与x轴相切又与直线L相切于点B，若存在，求出圆心P的坐标，若不存在，请说明理由。‎ ‎【062】如图13-1至图13-5，⊙O均作无滑动滚动，⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置，⊙O的周长为c．‎ 阅读理解：‎ 图13-1‎ A O1‎ O O2‎ B B 图13-2‎ A ‎ C n°‎ D O1‎ O2‎ B 图13-3‎ O2‎ O3‎ O A ‎ O1‎ C O4‎ ‎（1）如图13-1，⊙O从⊙O1的位置出发，沿AB滚动到 ‎⊙O2的位置，当AB = c时，⊙O恰好自转1周．‎ ‎（2）如图13-2，∠ABC相邻的补角是n°，⊙O在 ‎∠ABC外部沿A-B-C滚动，在点B处，必须由 ‎⊙O1的位置旋转到⊙O2的位置，⊙O绕点B旋 转的角∠O1BO2 = n°，⊙O在点B处自转周．‎ 实践应用：‎ ‎（1）在阅读理解的（1）中，若AB = ‎2c，则⊙O自 转 周；若AB = l，则⊙O自转 周．在 阅读理解的（2）中，若∠ABC = 120°，则⊙O 在点B处自转 周；若∠ABC = 60°，则⊙O 在点B处自转 周．‎ ‎（2）如图13-3，∠ABC=90°，AB=BC=c．⊙O从 ‎⊙O1的位置出发，在∠ABC外部沿A-B-C滚动 到⊙O4的位置，⊙O自转 周．‎ O A B C 图13-4‎ D 拓展联想：‎ ‎（1）如图13-4，△ABC的周长为l，⊙O从与AB相切于点D的位置出发，在△ABC外部，按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，⊙O自转了多少周？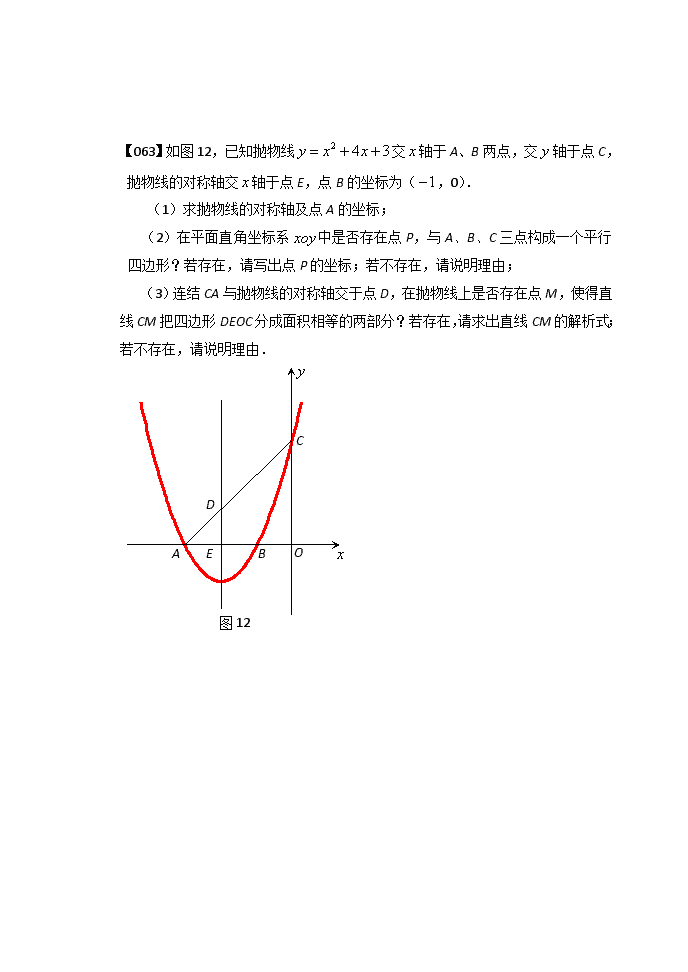请说明理由．‎ ‎（2）如图13-5，多边形的周长为l，⊙O从与某边相切于 D 图13-5‎ O 点D的位置出发，在多边形外部，按顺时针方向沿多 边形滚动，又回到与该边相切于点D的位置，直接写 出⊙O自转的周数．‎ ‎【063】如图12，已知抛物线交轴于A、B两点，交轴于点C，抛物线的对称轴交轴于点E，点B的坐标为（，0）．‎ ‎（1）求抛物线的对称轴及点A的坐标；‎ ‎（2）在平面直角坐标系中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；‎ O D B C A E 图12‎ ‎（3）连结CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．‎ ‎【064】如图，抛物线的顶点为A，与y 轴交于点B．‎ ‎（1）求点A、点B的坐标．‎ ‎（2）若点P是x轴上任意一点，求证：．‎ ‎（3）当最大时，求点P的坐标． ‎ B O A ‎·‎ x y 第28题图 ‎【065】如图11，AB是⊙O的直径，弦BC=‎2cm，∠ABC=60º．‎ ‎ （1）求⊙O的直径；‎ ‎（2）若D是AB延长线上一点，连结CD，当BD长为多少时，CD与⊙O相切；‎ ‎（3）若动点E以‎2cm/s的速度从A点出发沿着AB方向运动，同时动点F以‎1cm/s的速度从B点出发沿BC方向运动，设运动时间为，连结EF，当为何值时，△BEF为直角三角形．‎ 图10（3）‎ A B C O E F A B C O D 图10（1）‎ A B O E F C 图10（2）‎ ‎【066】如图，反比例函数y＝(x＞0)的图象与一次函数y＝－x＋的图象交于A、B两点，点C的坐标为(1，)，连接AC，AC∥y轴．‎ ‎(1)求反比例函数的解析式及点B的坐标；‎ ‎(2)现有一个直角三角板，让它的直角顶点P在反比例函数图象上A、B之间的部分滑动(不与A、B重合)，两直角边始终分别平行于x轴、y轴，且与线段AB交于M、N两点，试判断P点在滑动过程中△PMN是否与△CBA总相似？简要说明判断理由．‎ ‎【067】如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90º，AB＝‎12cm，AD＝‎8cm，BC＝‎22cm，AB为⊙O的直径，动点P从点A开始沿AD边向点D以‎1cm/s的速度运动，动点Q从点C开始沿CB边向点B以‎2cm/s的速度运动，P、Q分别从点A、C同时出发，当其中一点到达端点时，另一个动点也随之停止运动．设运动时间为t(s)．‎ ‎(1)当t为何值时，四边形PQCD为平行四边形？‎ ‎(2)当t为何值时，PQ与⊙O相切？‎ A B O C D P Q ‎【068】如图12，在直角梯形OABC中， OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F．设动点P、Q运动时间为t（单位：秒）．‎ ‎（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；‎ ‎（2）当t=2秒时，求梯形OFBC的面积；‎ ‎（3）当t为何值时，△PQF是等腰三角形？请写出推理过程．‎ ‎069】如图11，已知二次函数的图象与轴相交于两个不同的点、，与轴的交点为．设的外接圆的圆心为点．‎ ‎（1）求与轴的另一个交点D的坐标；‎ ‎（2）如果恰好为的直径，且的面积等于，求和的值． ‎ ‎【070】如图所示，菱形的边长为‎6厘米，．从初始时刻开始，点、同时从点出发，点以‎1厘米/秒的速度沿的方向运动，点以‎2厘米/秒的速度沿的方向运动，当点运动到点时，、两点同时停止运动，设、运动的时间为秒时，与重叠部分的面积为平方厘米（这里规定：点和线段是面积为的三角形），解答下列问题： ‎ ‎（1）点、从出发到相遇所用时间是 秒；‎ ‎（2）点、从开始运动到停止的过程中，当是等边三角形时的值是 秒；‎ ‎（3）求与之间的函数关系式．‎ P Q A B C D ‎（第28题）‎ ‎【071】已知：抛物线的对称轴为与轴交于两点，与轴交于点其中、‎ ‎（1）求这条抛物线的函数表达式．‎ ‎（2）已知在对称轴上存在一点P，使得的周长最小．请求出点P的坐标．‎ ‎（3）若点是线段上的一个动点（不与点O、点C重合）．过点D作交轴于点连接、．设的长为，的面积为．求与之间的函数关系式．试说明是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．‎ A C x y B O ‎（第24题图）‎ ‎【072】如图1所示，直角梯形OABC的顶点A、C分别在y轴正半轴与轴负半轴上.过点B、C作直线．将直线平移，平移后的直线与轴交于点D，与轴交于点E．‎ ‎（1）将直线向右平移，设平移距离CD为(t0)，直角梯形OABC被直线扫过的面积（图中阴影部份）为，关于的函数图象如图2所示， OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．‎ ‎①求梯形上底AB的长及直角梯形OABC的面积；‎ ‎②当时，求S关于的函数解析式；‎ ‎（2）在第（1）题的条件下，当直线向左或向右平移时（包括与直线BC重合），在直线AB上是否存在点P，使为等腰直角三角形?若存在，请直接写出所有满足条件的点P的坐标;若不存在，请说明理由．‎ ‎ ‎ ‎【073】)如图，半径为2的⊙O内有互相垂直的两条弦AB、CD相交于P点．‎ ‎(1)求证：PA·PB=PC·PD；‎ ‎(2)设BC的中点为F，连结FP并延长交AD于E，求证：EF⊥AD：‎ ‎(3)若AB=8，CD=6，求OP的长．‎ 第23题图 ‎【074】如图，在平面直角坐标系中，点的坐标为，以点为圆心，8为半径的圆与轴交于两点，过作直线与轴负方向相交成60°的角，且交轴于点，以点为圆心的圆与轴相切于点．‎ ‎（1）求直线的解析式；‎ O y x C D B A O1‎ O2‎ ‎60°‎ ‎（第22题）‎ l ‎（2）将以每秒1个单位的速度沿轴向左平移，当第一次与外切时，求平移的时间．‎ ‎【075】如图11，已知抛物线（）与轴的一个交点为，与y轴的负半轴交于点C，顶点为D．‎ ‎（1）直接写出抛物线的对称轴，及抛物线与轴的另一个交点A的坐标；‎ ‎（2）以AD为直径的圆经过点C．‎ ‎①求抛物线的解析式；‎ ‎②点在抛物线的对称轴上，点在抛物线上，且以四点为顶点的四边形为平行四边形，求点的坐标． ‎ O x y A B C D 图11‎ ‎【076】如图，抛物线与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.‎ ‎（1）求C点的坐标及抛物线的解析式；‎ ‎（2）将△BCH绕点B按顺时针旋转90°后 再沿x轴对折得到 ‎△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；‎ ‎（3）设过点E的直线交AB边于点P，交CD边于点Q. 问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.‎ ‎【077】已知直线与轴轴分别交于点A和点B，点B的坐标为（0，6）‎ ‎（1）求的值和点A的坐标；‎ ‎（2）在矩形OACB中，点P是线段BC上的一动点，直线PD⊥AB于点D，与轴交于点E，设BP=，梯形PEAC的面积为。‎ ‎①求与的函数关系式，并写出的取值范围；‎ ‎②⊙Q是△OAB的内切圆，求当PE与⊙Q相交的弦长为2.4时点P的坐标。‎ ‎【078】如图 12，已知直线过点和，是轴正半轴上的动点，的垂直平分线交于点，交轴于点． ‎ ‎（1）直接写出直线的解析式； ‎ ‎（2）设，的面积为，求关于t的函数关系式；并求出当时，的最大值； ‎ ‎（3）直线过点且与轴平行，问在上是否存在点， 使得是以为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．‎ L A O M P B x y L1‎ 图12‎ Q ‎【079】如图，在平面直角坐标系中，若、的长是关于的一元二次方程的两个根，且 ‎ （1）求的值．‎ ‎ （2）若为轴上的点，且求经过、两点的直线的解析式，并判断与是否相似？‎ ‎ （3）若点在平面直角坐标系内，则在直线上是否存在点使以、、、为顶点的四边形为菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．‎ x y A D B O C ‎28题图 ‎【080】已知：等边三角形的边长为‎4厘米，长为‎1厘米的线段在的边上沿方向以‎1厘米/秒的速度向点运动（运动开始时，点与点重合，点到达点时运动终止），过点分别作边的垂线，与的其它边交于两点，线段运动的时间为秒．‎ ‎（1）线段在运动的过程中，为何值时，四边形恰为矩形？并求出该矩形的面积；‎ ‎（2）线段在运动的过程中，四边形的面积为，运动的时间为．求四边形的面积随运动时间变化的函数关系式，并写出自变量的取值范围．‎ C P Q B A M N ‎【061】解（1）A（，0），B（0，3） 2分（每对一个给1分）‎ ‎（2）满分3分．其中过F作出垂线1分，作出BF中垂线1分，找出圆心并画出⊙P给1分． （注：画垂线PF不用尺规作图的不扣分）‎ ‎（3）过点P作PD⊥轴于D，则PD=，BD=， 6分 y x O A B D P F PB=PF=，∵△BDP为直角三形，∴ ‎ ‎∴，即 即∴与的函数关系为 ‎（4）存在 解法1：∵⊙P与轴相切于点F，且与直线相切于点B ‎∴，∵，∴‎ ‎∵AF= ， ∴，∴ 11分 把代入，得 ‎∴点P的坐标为（1，）或（9，15）12分 ‎【062】解：实践应用（1）2；．；．（2）．‎ 拓展联想（1）∵△ABC的周长为l，∴⊙O在三边上自转了周． ‎ 又∵三角形的外角和是360°，‎ ‎∴在三个顶点处，⊙O自转了（周）． ‎ ‎∴⊙O共自转了（+1）周． ‎ ‎（2）+1．‎ ‎【063】（1）① 对称轴 （2分）‎ ‎② 当时，有，解之，得 ，‎ ‎∴ 点A的坐标为（，0）． （4分）‎ ‎（2）满足条件的点P有3个，分别为（，3），（2，3），（，）． （7分）‎ ‎（3）存在．当时， ∴ 点C的坐标为（0，3）‎ ‎∵ DE∥轴，AO3，EO2，AE1，CO3‎ ‎∴ ∽ ∴ 即 ∴ DE1 （9分）‎ ‎∴ 4‎ 在OE上找点F，使OF，此时2，直线CF把四边形DEOC 分成面积相等的两部分，交抛物线于点M． （10分）‎ 设直线CM的解析式为，它经过点．则 （11分）‎ 解之，得 ∴ 直线CM的解析式为 （12分）‎ B O A ‎·‎ x y 第28题图 P H ‎【064】解：（1）抛物线与y轴的交于点B，令x=0得y=2．‎ ‎∴B（0，2） ‎ ‎∵ ∴A（—2，3）‎ ‎（2）当点P是 AB的延长线与x轴交点时，‎ ‎．‎ 当点P在x轴上又异于AB的延长线与x轴的交点时，‎ 在点P、A、B构成的三角形中，．‎ 综合上述： ‎ ‎（3）作直线AB交x轴于点P，由（2）可知：当PA—PB最大时，点P是所求的点 8分 作AH⊥OP于H．∵BO⊥OP，∴△BOP∽△AHP ‎ ∴ 由（1）可知：AH=3、OH=2、OB=2，∴OP=4，故P（4，0） ‎ ‎【065】解：（1）∵AB是⊙O的直径（已知）‎ ‎ ∴∠ACB＝90º（直径所对的圆周角是直角）‎ ‎ ∵∠ABC＝60º（已知）‎ ‎ ∴∠BAC＝180º－∠ACB－∠ABC＝ 30º（三角形的内角和等于180º）‎ ‎ ∴AB＝2BC＝‎4cm（直角三角形中，30º锐角所对的直角边等于斜边的一半）‎ ‎ 即⊙O的直径为‎4cm．‎ ‎（2）如图10（1）CD切⊙O于点C，连结OC，则OC＝OB＝1/2·AB＝‎2cm．‎ ‎∴CD⊥CO（圆的切线垂直于经过切点的半径）‎ ‎∴∠OCD＝90º（垂直的定义） ∵∠BAC＝ 30º（已求）‎ ‎∴∠COD＝2∠BAC＝ 60º ∴∠D＝180º－∠COD－∠OCD＝ 30º∴OD＝2OC＝‎4cm ∴BD＝OD－OB＝4－2＝2（cm）‎ ‎ ∴当BD长为‎2cm，CD与⊙O相切．‎ ‎（3）根据题意得：‎ BE＝（4－2t）cm，BF＝tcm；‎ 如图10（2）当EF⊥BC时，△BEF为直角三角形，此时△BEF∽△BAC ‎∴BE：BA＝BF：BC即：（4－2t）：4＝t：2解得：t＝1‎ 如图10（3）当EF⊥BA时，△BEF为直角三角形，此时△BEF∽△BCA ‎∴BE：BC＝BF：BA即：（4－2t）：2＝t：4解得：t＝1.6‎ ‎∴当t＝1s或t＝1.6s时，△BEF为直角三角形．‎ ‎【066】（1）由得，代入反比例函数中，得 ‎∴反比例函数解析式为： 2分 解方程组由化简得：‎ ‎，所以 5分 ‎ （2）无论点在之间怎样滑动，与总能相似．因为两点纵坐标相等，所以轴．‎ 又因为轴，所以为直角三角形．‎ 同时也是直角三角形，‎ ‎ 8分 ‎（在理由中只要能说出轴，即可得分．）‎ ‎【067】（1）解：∵直角梯形 O A P D B Q C 当时，四边形 为平行四边形．‎ 由题意可知：‎ 当时，四边形为平行四边形． 3分 O A P D B Q C H E ‎（2）解：设与相切于点 过点作垂足为 直角梯形 由题意可知：‎ 为的直径，‎ 为的切线 ‎ 5分 在中，，‎ 即：，，‎ ‎，因为在边运动的时间为秒 而，（舍去），当秒时，与相切． 8分 ‎【068】解：（1）如图4，过B作 则 过Q作 则 ‎ （2分）‎ 要使四边形PABQ是等腰梯形，则，‎ 即 或（此时是平行四边形，不合题意，舍去） （3分）‎ ‎（2）当时，。‎ ‎ （4分）‎ ‎ （5分）‎ ‎ （6分）‎ ‎（3）①当时，则 ‎ （7分）‎ ‎②当时，‎ 即 （8分）‎ ‎③当时， （9分）‎ 综上，当时，△PQF是等腰三角形． （10分）‎ ‎【069】解 （1）易求得点的坐标为 由题设可知是方程即 的两根，‎ 所以，所 （1分）‎ 如图3，∵⊙P与轴的另一个交点为D，由于AB、CD是⊙P的两条相交弦，设它们的交点为点O，连结DB，∴△AOC∽△DOC，则 （2分）‎ 由题意知点在轴的负半轴上，从而点D在轴的正半轴上，‎ 所以点D的坐标为（0，1） （3分）‎ ‎（2）因为AB⊥CD， AB又恰好为⊙P的直径，则C、D关于点O对称，‎ 所以点的坐标为，即 （4分）‎ 又，‎ 所以解得 （6分）‎ ‎【070】解：（1）6．（2）8． （3分）‎ ‎（3）①当0时，‎ Q1‎ A B C D Q2‎ P3‎ Q3‎ E P2‎ P1‎ O ‎． （5分）‎ ‎②当3时，‎ ‎= （7分）‎ ‎③当时，设与交于点．‎ ‎(解法一)‎ 过作则为等边三角形．‎ ‎．‎ ‎． （10分）‎ ‎（解法二）‎ 如右图，过点作于点，，于点 过点作交延长线于点．‎ P3‎ O A B C D Q3‎ G H F 又 又 ‎ （10分）‎ ‎【071】解：（1）由题意得，解得 ‎∴此抛物线的解析式为 3分 ‎（2）连结、.因为的长度一定，所以周长最小，就是使最小.点关于对称轴的对称点是点，与对称轴的交点即为所求的点.‎ ‎（第24题图）‎ O A C x y B E P D 设直线的表达式为 则 解得 ‎∴此直线的表达式为……5分 把代入得∴点的坐标为 6分 ‎（3）存在最大值 7分 理由：∵即 ‎∴∴即 ‎∴‎ 方法一：‎ 连结 ‎=‎ ‎= 8分 ‎∵，∴当时， 9分 方法二：‎ ‎ =‎ ‎= 8分 ‎∵，∴当时， 9分 ‎【072】解：（1）①，，，S梯形OABC=12 ‎ ‎②当时，直角梯形OABC被直线扫过的面积=直角梯形OABC面积－直角三角开DOE面积 ‎ ‎（2） 存在 ， ‎ 对于第（2）题我们提供如下详细解答（评分无此要求）.下面提供参考解法二：‎ ‎ 以点D为直角顶点，作轴 ‎ ‎ 设.（图示阴影），在上面二图中分别可得到点的生标为P（－12，4）、P（－4，4）E点在0点与A点之间不可能；‎ ‎② 以点E为直角顶点 ‎ ‎ 同理在②二图中分别可得点的生标为P（－，4）、P（8，4）E点在0点下方不可能.‎ 以点P为直角顶点 同理在③二图中分别可得点的生标为P（－4，4）（与①情形二重合舍去）、P ‎（4，4），‎ E点在A点下方不可能.‎ 综上可得点的生标共5个解，分别为P（－12，4）、P（－4，4）、P（－，4）、‎ P（8，4）、P（4，4）．‎ 下面提供参考解法二：‎ 以直角进行分类进行讨论（分三类）：‎ 第一类如上解法⑴中所示图 ‎，直线的中垂线方程：，令得．由已知可得即化简得解得 ；‎ 第二类如上解法②中所示图 ‎，直线的方程：，令得．由已知可得即化简得解之得 ，‎ 第三类如上解法③中所示图 ‎，直线的方程：，令得．由已知可得即解得 ‎（与重合舍去）．‎ 综上可得点的生标共5个解，分别为P（－12，4）、P（－4，4）、P（－，4）、‎ P（8，4）、P（4，4）．‎ 事实上，我们可以得到更一般的结论：‎ 如果得出设，则P点的情形如下 直角分类情形 ‎【073】(1)∵∠A、∠C所对的圆弧相同，∴∠A＝∠C．‎ ‎∴Rt△APD∽Rt△CPB，∴，∴PA·PB＝PC·PD；………………………3分 ‎(2)∵F为BC的中点，△BPC为Rt△，∴FP＝FC，∴∠C＝∠CPF．‎ 又∠C＝∠A，∠DPE＝∠CPF，∴∠A＝∠DPE．∵∠A＋∠D＝90°，‎ ‎∴∠DPE＋∠D＝90°．∴EF⊥AD．‎ ‎(3)作OM⊥AB于M，ON⊥CD于N，同垂径定理：‎ O y x C D B A D1‎ O1‎ O2‎ O3‎ P ‎60°‎ ‎（第22题答图）‎ l ‎∴OM2＝(2)2－42＝4，ON2＝(2)2－32＝11‎ 又易证四边形MONP是矩形，‎ ‎∴OP＝ ‎ ‎【074】（1）解：由题意得，‎ 点坐标为．在中，，‎ 点的坐标为． ‎ 设直线的解析式为，由过两点，得 解得直线的解析式为：．‎ ‎（2）如图，设平移秒后到处与第一次外切于点，‎ 与轴相切于点，连接．则 轴，，‎ 在中，． 6分 ‎，，‎ ‎（秒）平移的时间为5秒． 8分 ‎【075】解：（1）对称轴是直线：，‎ 点A的坐标是（3，0）． 2分 ‎（说明：每写对1个给1分，“直线”两字没写不扣分）‎ ‎（2）如图11，连接AC、AD，过D作于点M，‎ 解法一：利用 ‎∵点A、D、C的坐标分别是A （3，0），D（1，）、C（0，），‎ ‎∴AO＝3，MD=1．由得∴ 3分 又∵∴由 得 ‎ ‎∴函数解析式为： 6分 解法二：利用以AD为直径的圆经过点C ‎∵点A、D的坐标分别是A （3，0） 、D（1，）、C（0，），‎ ‎∴，，∵‎ ‎∴…① 又∵…② 4分 由①、②得 ∴函数解析式为： 6分 ‎（3）如图所示，当BAFE为平行四边形时，则∥，并且＝．‎ ‎ ∵=4，∴=4 ，由于对称为，∴点F的横坐标为5． 7分 y x O A B C D 图11‎ E F 将代入得，∴F（5，12）． ‎ 根据抛物线的对称性可知，在对称轴的左侧 抛物线上也存在点F，使得四边形BAEF是 平行四边形，此时点F坐标为（，12）． ‎ 当四边形BEAF是平行四边形时，‎ 点F即为点D，此时点F的坐标为（1，）． ‎ 综上所述，点F的坐标为（5，12），‎ ‎（，12）或（1，）．‎ ‎【076】解：（1）∵四边形OBHC为矩形，∴CD∥AB，‎ ‎ 又D（5，2）， ∴C（0，2），OC=2 . ‎ ‎ ∴ 解得 ‎ ∴抛物线的解析式为： …… 4分 ‎（2）点E落在抛物线上. 理由如下：……… 5分 由y = 0，得. 解得x1=1，x2=4. ∴A（4，0），B（1，0）. ‎ ‎ ∴OA=4，OB=1. 由矩形性质知：CH=OB=1，BH=OC=2，∠BHC=90°，‎ 由旋转、轴对称性质知：EF=1，BF=2，∠EFB=90°，∴点E的坐标为（3，－1）. ‎ 把x=3代入，得， ∴点E在抛物线上. ‎ ‎（3）法一：存在点P（a，0），延长EF交CD于点G，易求OF=CG=3，PB=a－1.‎ ‎ S梯形BCGF = 5，S梯形ADGF = 3，记S梯形BCQP = S1，S梯形ADQP = S2，‎ ‎ 下面分两种情形： ①当S1∶S2 =1∶3时，，‎ 此时点P在点F（3，0）的左侧，则PF = 3－a，由△EPF∽△EQG，得，则QG=9－‎3a，∴CQ=3－(9－‎3a) =‎3a －6，由S1=2，得，解得； ‎ ‎②当S1∶S2=3∶1时，，此时点P在点F（3，0）的右侧，则PF = a－3，由△EPF∽△EQG，得QG = ‎3a－9，∴CQ = 3 +（‎3 a－9）= ‎3 a－6，‎ 由S1= 6，得，解得，综上所述：所求点P的坐标为（，0）或（，0）……… 14分 ‎ 法二：存在点P（a，0）. 记S梯形BCQP = S1，S梯形ADQP = S2，易求S梯形ABCD = 8.‎ 当PQ经过点F（3，0）时，易求S1=5，S2 = 3，此时S1∶S2不符合条件，故a≠3.‎ 设直线PQ的解析式为y = kx+b(k≠0)，则，解得，‎ ‎∴. 由y = 2得x = ‎3a－6，∴Q（‎3a－6，2） ……… 10分 ‎∴CQ = ‎3a－6，BP = a－1，.‎ 下面分两种情形：①当S1∶S2 = 1∶3时，= 2；‎ ‎∴‎4a－7 = 2，解得；……………………………………………… 12分 ‎②当S1∶S2 = 3∶1时，； ∴‎4a－7 = 6，解得；‎ 综上所述：所求点P的坐标为（，0）或（，0）………… 14分 ‎[说明：对于第（3）小题，只要考生能求出或两个答案，就给6分. ]‎ ‎【077】解：（1）把B（0，6）代入，得＝6………………………1分 ‎ 把＝0代入，得＝8‎ ‎∴点A的坐标为（8，0）…………… 3分 ‎（2）在矩形OACB中，AC＝OB＝6，‎ BC＝OA＝8，∠C＝90°‎ ‎∴AB＝‎ ‎∵PD⊥AB∴∠PDB=∠C＝90°‎ ‎，∴∴∴‎ 又∵BC∥AE，∴△PBD∽△EAD ‎∴，即，∴‎ ‎∵，∴ （）……………………………7分 （注：写成不扣分）‎ ‎② ⊙Q是△OAB的内切圆 ，可设⊙Q的半径为r ‎∵,解得r=2.………………………………………8分 设⊙Q与OB、AB、OA分别切于点F、G、H 可知，OF＝2∴BF＝BG＝OB－OF＝6－2＝4，设直线PD与⊙Q交于点 I、J ，过Q作QM⊥IJ于点M，连结IQ、QG， ∵QI＝2， ‎ ‎ ∴ ∴ 在矩形GQMD中，GD＝QM＝1.6‎ ‎∴BD＝BG+GD＝4+1.6＝5.6，由，得 ‎∴点P的坐标为（7，6）…………………………………………………………………11分 当PE在圆心Q的另一侧时，同理可求点P的坐标为（3，6）………………………12分 综上，P点的坐标为（7，6）或（3，6）．………………………………………………13分。‎ ‎【078】（1） 2分 ‎（2）∵，∴点的横坐标为，‎ ‎①当，即时，，‎ ‎∴． 3分 ‎②当时，，‎ ‎∴．∴ 4分 当，即时，，‎ ‎∴当时，有最大值． 6分 ‎（3）由，所以是等腰直角三角形，若在上存在点，使得是以为直角顶点的等腰直角三角形，则，所以，又轴，则，两点关于直线对称，所以，得． 7 分 L A O P B x y L1‎ ‎23题图-1‎ Q C 下证．连，则四边形是正方形． ‎ 法一：（i）当点在线段上，在线段上 ‎（与不重合）时，如图–1． ‎ 由对称性，得， ‎ ‎∴ ， ‎ ‎∴ ． 8分 ‎（ii）当点在线段的延长线上，在线段上时，如图–2，如图–3 ‎ ‎∵， ∴． 9分 ‎ ‎（iii）当点与点重合时，显然． ‎ 综合（i）（ii）（iii），． ‎ y L A O P B x L1‎ ‎23题图-3‎ Q C ‎2‎ ‎1‎ ‎∴在上存在点，使得是以为直角顶点的等腰直角三角形． 11 分 ‎ L A O P B x L1‎ ‎23题图-2‎ Q C ‎2‎ ‎1‎ y 法二：由，所以是等腰直角三角形，若在上存在点，使得是以为直角顶点的等腰直角三角形，则，所以，又轴， 则，两点关于直线对称，所以，得． 7 分 ‎ 延长与交于点． ‎ ‎（i）如图–4，当点在线段上（与不重合）时，‎ ‎∵四边形是正方形， ‎ ‎∴四边形和四边形都是矩形，和都是等腰直角三角形．‎ ‎∴． ‎ L A O P B x y L1‎ ‎23题图-1‎ Q C 又∵， ∴， ‎ ‎ ∴， ‎ ‎∴， ‎ 又∵，‎ ‎∴． ‎ ‎ ∴． 8分 ‎（ii）当点与点重合时，显然． 9分 ‎ ‎（iii）在线段的延长线上时，如图–5， ‎ ‎∵，∠1=∠2 ‎ ‎ ∴ ‎ 综合（i）（ii）（iii），． ‎ ‎∴在上存在点，使得是以为直角顶点的等腰直角三角形． 11分 ‎23题图-4‎ L A O M P B x y L1‎ Q C N y L A O P B x L1‎ ‎23题图-5‎ Q C ‎2‎ ‎1‎ 法三：由，所以是等腰直角三角形，若在上存在点，使得是以为直角顶点的等腰直角三角形，则，所以，又轴， ‎ ‎ 则，O两点关于直线对称，所以，得． 9分 连，∵，，，‎ ‎∴，‎ ‎．‎ ‎∴，∴． 10分 ‎∴在上存在点，使得是以为直角顶点的等腰直角三角形． 11分 ‎【079】解：（1）解得 ‎ ， 1分 在中，由勾股定理有， ‎ ‎（2）∵点在轴上，，，‎ ‎ 1分 由已知可知D（6，4），设当时有 解得，同理时， 1分 在中，‎ 在中，，，‎ ‎（3）满足条件的点有四个， 4分 说明：本卷中所有题目，若由其它方法得出正确结论，可参照本评 C P Q B A M D N ‎【080】（1）过点作，垂足为．则，‎ 当运动到被垂直平分时，四边形是矩形，‎ 即时，四边形是矩形，‎ 秒时，四边形是矩形．‎ C P Q B A M N ‎，‎ ‎（2）当时，‎ C P Q B A M N 当时 C P Q B A M N 当时，‎ ‎ 10分