2014遵义中考数学试题解析版 21页

贵州省遵义市2014年中考数学试卷 ‎　‎ 一、选择题（本题共10小题，每小题3分，共30分）‎ ‎1．（3分）（2014•遵义）﹣3+（﹣5）的结果是（　　）‎ ‎　‎ A．‎ ‎﹣2‎ B．‎ ‎﹣8‎ C．‎ ‎8‎ D．‎ ‎2‎ 考点：‎ 有理数的加法．‎ 分析：‎ 根据同号两数相加，取相同的符号，并把绝对值相加，可得答案．‎ 解答：‎ 解：原式=﹣（3+5）‎ ‎=﹣8．‎ 故选：B．‎ 点评：‎ 本题考查了有理数的加法，先确定和的符号，再进行绝对值得运算．‎ ‎　‎ ‎2．（3分）（2014•遵义）观察下列图形，是中心对称图形的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 中心对称图形 分析：‎ 根据中心对称图形的概念对各选项分析判断后利用排除法求解．‎ 解答：‎ 解：A、不是中心对称图形，故本选项错误；‎ B、不是中心对称图形，故本选项错误；‎ C、是中心对称图形，故本选项正确；‎ D、不是中心对称图形，故本选项错误．‎ 故选：C．‎ 点评：‎ 本题考查了中心对称图形的概念：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．中心对称图形是要寻找对称中心，旋转180度后两部分重合．‎ ‎　‎ ‎3．（3分）（2014•遵义）“着力扩大投资，突破重点项目建设”是遵义经济社会发展的主要任务之一．据统计，遵义市2013年全社会固定资产投资达1762亿元，把1762亿元这个数字用科学记数法表示为（　　）‎ ‎　‎ A．‎ ‎1762×108‎ B．‎ ‎1.762×1010‎ C．‎ ‎1.762×1011‎ D．‎ ‎1.762×1012‎ 考点：‎ 科学记数法—表示较大的数．‎ 分析：‎ 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ 解答：‎ 解：将1762亿用科学记数法表示为：1.762×1011．‎ 故选：C．‎ 点评：‎ 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎　‎ ‎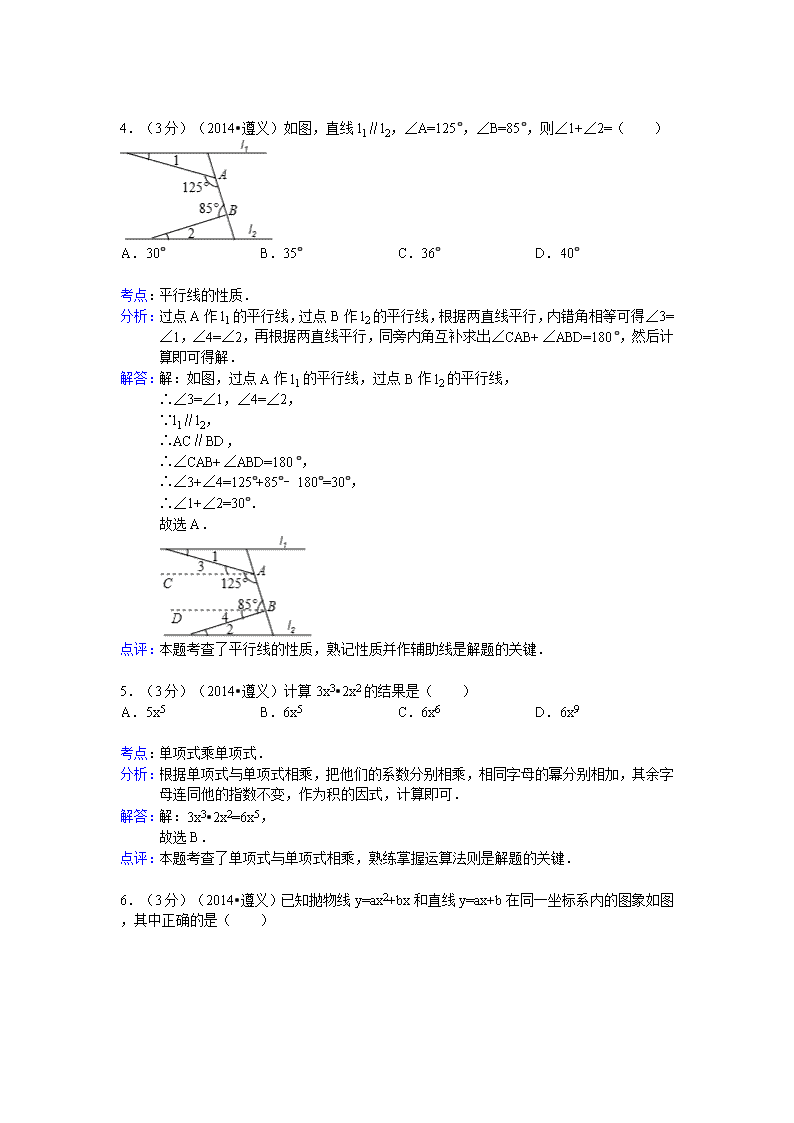4．（3分）（2014•遵义）如图，直线l1∥l2，∠A=125°，∠B=85°，则∠1+∠2=（　　）‎ ‎　‎ A．‎ ‎30°‎ B．‎ ‎35°‎ C．‎ ‎36°‎ D．‎ ‎40°‎ 考点：‎ 平行线的性质．‎ 分析：‎ 过点A作l1的平行线，过点B作l2的平行线，根据两直线平行，内错角相等可得∠3=∠1，∠4=∠2，再根据两直线平行，同旁内角互补求出∠CAB+∠ABD=180°，然后计算即可得解．‎ 解答：‎ 解：如图，过点A作l1的平行线，过点B作l2的平行线，‎ ‎∴∠3=∠1，∠4=∠2，‎ ‎∵l1∥l2，‎ ‎∴AC∥BD，‎ ‎∴∠CAB+∠ABD=180°，‎ ‎∴∠3+∠4=125°+85°﹣180°=30°，‎ ‎∴∠1+∠2=30°．‎ 故选A．‎ 点评：‎ 本题考查了平行线的性质，熟记性质并作辅助线是解题的关键．‎ ‎　‎ ‎5．（3分）（2014•遵义）计算3x3•2x2的结果是（　　）‎ ‎　‎ A．‎ ‎5x5‎ B．‎ ‎6x5‎ C．‎ ‎6x6‎ D．‎ ‎6x9‎ 考点：‎ 单项式乘单项式．‎ 分析：‎ 根据单项式与单项式相乘，把他们的系数分别相乘，相同字母的幂分别相加，其余字母连同他的指数不变，作为积的因式，计算即可．‎ 解答：‎ 解：3x3•2x2=6x5，‎ 故选B．‎ 点评：‎ 本题考查了单项式与单项式相乘，熟练掌握运算法则是解题的关键．‎ ‎　‎ ‎6．（3分）（2014•遵义）已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图，其中正确的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 二次函数的图象；一次函数的图象．‎ 分析：‎ 本题可先由二次函数图象得到字母系数的正负，再与一次函数和反比例函数的图象相比较看是否一致．逐一排除．‎ 解答：‎ 解：A、由二次函数的图象可知a＜0，此时直线y=ax+b经过二、四象限，故A可排除；‎ B、二次函数的图象可知a＜0，对称轴在y轴的右侧，可知a、b异号，b＞0，此时直线y=ax+b经过一、二、四象限，故B可排除；‎ C、二次函数的图象可知a＞0，此时直线y=ax+b经过一、三，故C可排除；‎ 正确的只有D．‎ 故选：D．‎ 点评：‎ 此题主要考查了一次函数图象与二次函数图象，应该识记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．‎ ‎　‎ ‎7．（3分）（2014•遵义）有一组数据7、11、12、7、7、8、11．下列说法错误的是（　　）‎ ‎　‎ A．‎ 中位数是7‎ B．‎ 平均数是9‎ C．‎ 众数是7‎ D．‎ 极差是5‎ 考点：‎ 极差；加权平均数；中位数；众数．‎ 分析：‎ 根据中位数、平均数、极差、众数的概念求解．‎ 解答：‎ 解：这组数据按照从小到大的顺序排列为：7、7、7、8、11、11、12，‎ 则中位数为：8，‎ 平均数为：=9，‎ 众数为：7，‎ 极差为：12﹣7=5．‎ 故选A．‎ 点评：‎ 本题考查了中位数、平均数、极差、众数的知识，掌握各知识点的概念是解答本题的关键．‎ ‎　‎ ‎8．（3分）（2014•遵义）若a+b=2，ab=2，则a2+b2的值为（　　）‎ ‎　‎ A．‎ ‎6‎ B．‎ ‎4‎ C．‎ ‎3‎ D．‎ ‎2‎ 考点：‎ 完全平方公式．‎ 分析：‎ 利用a2+b2=（a+b）2﹣2ab代入数值求解．‎ 解答：‎ 解：a2+b2=（a+b）2﹣2ab=8﹣4=4，‎ 故选：B．‎ 点评：‎ 本题主要考查了完全平方公式的应用，解题的关键是牢记完全平方公式，灵活运用它的变化式．‎ ‎　‎ ‎9．（3分）（2014•遵义）如图，边长为2的正方形ABCD中，P是CD的中点，连接AP并延长交BC的延长线于点F，作△CPF的外接圆⊙O，连接BP并延长交⊙O于点E，连接EF，则EF的长为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 相似三角形的判定与性质；正方形的性质；圆周角定理．菁优网版权所有 分析：‎ 先求出CP、BF长，根据勾股定理求出BP，根据相似得出比例式，即可求出答案．‎ 解答：‎ 解：∵四边形ABCD是正方形，‎ ‎∴∠ABC=∠PCF=90°，CD∥AB，‎ ‎∵F为CD的中点，CD=AB=BC=2，‎ ‎∴CP=1，‎ ‎∵PC∥AB，‎ ‎∴△FCP∽△FBA，‎ ‎∴==，‎ ‎∴BF=4，‎ ‎∴CF=4﹣2=2，‎ 由勾股定理得：BP==，‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠BCP=∠PCF=90°，‎ ‎∴PF是直径，‎ ‎∴∠E=90°=∠BCP，‎ ‎∵∠PBC=∠EBF，‎ ‎∴△BCP∽△BEF，‎ ‎∴=，‎ ‎∴=，‎ ‎∴EF=，‎ 故选D．‎ 点评：‎ 本题考查了正方形的性质，圆周角定理，相似三角形的性质和判定的应用，主要考查学生的推理能力和计算能力，题目比较好，难度适中．‎ ‎　‎ ‎10．（3分）（2014•遵义）如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B的长为（　　）‎ ‎　‎ A．‎ ‎2﹣‎ B．‎ C．‎ ‎﹣1‎ D．‎ ‎1‎ 考点：‎ 旋转的性质．菁优网版权所有 分析：‎ 连接BB′，根据旋转的性质可得AB=AB′，判断出△ABB′是等边三角形，根据等边三角形的三条边都相等可得AB=BB′，然后利用“边边边”证明△ABC′和△B′BC′全等，根据全等三角形对应角相等可得∠ABC′=∠B′BC′，延长BC′交AB′于D，根据等边三角形的性质可得BD⊥AB′，利用勾股定理列式求出AB，然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D，然后根据BC′=BD﹣C′D计算即可得解．‎ 解答：‎ 解：如图，连接BB′，‎ ‎∵△ABC绕点A顺时针方向旋转60°得到△AB′C′，‎ ‎∴AB=AB′，∠BAB′=60°，‎ ‎∴△ABB′是等边三角形，‎ ‎∴AB=BB′，‎ 在△ABC′和△B′BC′中，‎ ‎，‎ ‎∴△ABC′≌△B′BC′（SSS），‎ ‎∴∠ABC′=∠B′BC′，‎ 延长BC′交AB′于D，‎ 则BD⊥AB′，‎ ‎∵∠C=90°，AC=BC=，‎ ‎∴AB==2，‎ ‎∴BD=2×=，‎ C′D=×2=1，‎ ‎∴BC′=BD﹣C′D=﹣1．‎ 故选C．‎ 点评：‎ 本题考查了旋转的性质，全等三角形的判定与性质，等边三角形的判定与性质，等腰直角三角形的性质，作辅助线构造出全等三角形并求出BC′在等边三角形的高上是解题的关键，也是本题的难点．‎ ‎　‎ 二、填空题（本题共8小题，每小题4分，共32分）‎ ‎11．（4分）（2014•遵义）+=　4　．‎ 考点：‎ 二次根式的加减法．菁优网版权所有 分析：‎ 先化简，然后合并同类二次根式．‎ 解答：‎ 解：原式=3+=4．‎ 故答案为；4．‎ 点评：‎ 本题考查了二次根式的加减法，掌握二次根式的化简是解答本题的关键．‎ ‎　‎ ‎12．（4分）（2014•遵义）正多边形的一个外角等于20°，则这个正多边形的边数是　18　．‎ 考点：‎ 多边形内角与外角．菁优网版权所有 分析：‎ 根据任何多边形的外角和都是360度，利用360除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．‎ 解答：‎ 解：因为外角是20度，360÷20=18，则这个多边形是18边形．‎ 点评：‎ 根据外角和的大小与多边形的边数无关，由外角和求正多边形的边数，是常见的题目，需要熟练掌握．‎ ‎　‎ ‎13．（4分）（2014•遵义）计算：+的结果是　﹣1　．‎ 考点：‎ 分式的加减法．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 原式变形后利用同分母分式的减法法则计算即可得到结果．‎ 解答：‎ 解：原式=﹣‎ ‎=‎ ‎=﹣1．‎ 故答案为：﹣1．‎ 点评：‎ 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎14．（4分）（2014•遵义）关于x的一元二次方程x2﹣3x+b=0有两个不相等的实数根，则b的取值范围是　b＜　．‎ 考点：‎ 根的判别式．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 根据判别式的意义得到△=（﹣3）2﹣4b＞0，然后解不等式即可．‎ 解答：‎ 解：根据题意得△=（﹣3）2﹣4b＞0，‎ 解得b＜．‎ 故答案为b＜．‎ 点评：‎ 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．‎ ‎　‎ ‎15．（4分）（2014•遵义）有一圆锥，它的高为8cm，底面半径为6cm，则这个圆锥的侧面积是　60π　cm2．（结果保留π）‎ 考点：‎ 圆锥的计算．菁优网版权所有 分析：‎ 先根据圆锥的底面半径和高求出母线长，圆锥的侧面积是展开后扇形的面积，计算可得．‎ 解答：‎ 解：圆锥的母线==10cm，‎ 圆锥的底面周长2πr=12πcm，‎ 圆锥的侧面积=lR=×12π×10=60πcm2．‎ 故答案为60π．‎ 点评：‎ 本题考查了圆锥的计算，圆锥的高和圆锥的底面半径圆锥的母线组成直角三角形，扇形的面积公式为lR．‎ ‎　‎ ‎16．（4分）（2014•遵义）有一个正六面体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第2014次后，骰子朝下一面的点数是　3　． ‎ 考点：‎ 专题：正方体相对两个面上的文字；规律型：图形的变化类．菁优网版权所有 分析：‎ 观察图象知道点数三和点数四相对，点数二和点数五相对且四次一循环，从而确定答案．‎ 解答：‎ 解：观察图象知道点数三和点数四相对，点数二和点数五相对且四次一循环，‎ ‎∵2014÷4=503…2，‎ ‎∴滚动第2014次后与第二次相同，‎ ‎∴朝下的点数为3，‎ 故答案为：3．‎ 点评：‎ 本题考查了正方体相对两个面上的文字及图形的变化类问题，解题的关键是发现规律．‎ ‎　‎ ‎17．（4分）（2014•遵义）“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FE⊥AD，EG=15里，HG经过A点，则FH=　1.05　里．‎ 考点：‎ 相似三角形的应用．菁优网版权所有 分析：‎ 首先根据题意得到△GEA∽△AFH，然后利用相似三角形的对应边的比相等列出比例式求得答案即可．‎ 解答：‎ 解：EG⊥AB，FE⊥AD，HG经过A点，‎ ‎∴FA∥EG，EA∥FH，‎ ‎∴∠HFA=∠AEG=90°，∠FHA=∠EAG，‎ ‎∴△GEA∽△AFH，‎ ‎∴．‎ ‎∵AB=9里，DA=7里，EG=15里，‎ ‎∴FA=3.5里，EA=4.5里，‎ ‎∴，‎ 解得：FH=1.05里．‎ 故答案为：1.05．‎ 点评：‎ 本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形，难度不大．‎ ‎　‎ ‎18．（4分）（2014•遵义）如图，反比例函数y=（k＞0）的图象与矩形ABCO的两边相交于E，F两点，若E是AB的中点，S△BEF=2，则k的值为　8　．‎ 考点：‎ 反比例函数系数k的几何意义．菁优网版权所有 分析：‎ 设E（a，），则B纵坐标也为，代入反比例函数的y=，即可求得F的横坐标，则根据三角形的面积公式即可求得k的值．‎ 解答：‎ 解：设E（a，），则B纵坐标也为，‎ E是AB中点，所以F点横坐标为2a，代入解析式得到纵坐标：，‎ BF=﹣=，所以F也为中点，‎ S△BEF=2=，k=8．‎ 故答案是：8．‎ 点评：‎ 本题考查了反比例函数的性质，正确表示出BF的长度是关键．‎ ‎　‎ 三、解答题（本题共9小题，共88分）‎ ‎19．（6分）（2014•遵义）计算：﹣|﹣4|﹣2cos45°﹣（3﹣π）0．‎ 考点：‎ 实数的运算；零指数幂；特殊角的三角函数值．菁优网版权所有 分析：‎ 本题涉及零指数幂、绝对值、特殊角的三角函数值、二次根式化简四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．‎ 解答：‎ 解：原式=3﹣4﹣﹣1‎ ‎=2﹣5．‎ 点评：‎ 本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算．‎ ‎　‎ ‎20．（8分）（2014•遵义）解不等式组：，并把不等式组的解集在数轴上表示出来．‎ 考点：‎ 解一元一次不等式组；在数轴上表示不等式的解集．菁优网版权所有 分析：‎ 分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．‎ 解答：‎ 解：由①得，x≥﹣1，‎ 由②得，x＜4，‎ 故此不等式组的解集为：﹣1≤x＜4．‎ 在数轴上表示为：‎ ‎．‎ 点评：‎ 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．‎ ‎　‎ ‎21．（8分）（2014•遵义）如图，一楼房AB后有一假山，其坡度为i=1：，山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离BC=25米，与亭子距离CE=20米，小丽从楼房顶测得E点的俯角为45°，求楼房AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）‎ 考点：‎ 解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题．菁优网版权所有 专题：‎ 应用题．‎ 分析：‎ 过点E作EF⊥BC的延长线于F，EH⊥AB于点H，根据CE=20米，坡度为i=1：，分别求出EF、CF的长度，在Rt△AEH中求出AH，继而可得楼房AB的高．‎ 解答：‎ 解：过点E作EF⊥BC的延长线于F，EH⊥AB于点H，‎ 在Rt△CEF中，∵i===tan∠ECF，‎ ‎∴∠ECF=30°，‎ ‎∴EF=CE=10米，CF=10米，‎ ‎∴BH=EF=10米，HE=BF=BC+CF=（25+10）米，‎ 在Rt△AHE中，∵∠HAE=45°，‎ ‎∴AH=HE=（25+10）米，‎ ‎∴AB=AH+HB=（35+10）米．‎ 答：楼房AB的高为（35+10）米．‎ 点评：‎ 本题考查了解直角三角形的应用，涉及仰角俯角及坡度坡角的知识，构造直角三角形是解题关键．‎ ‎　‎ ‎22．（10分）（2014•遵义）小明、小军两同学做游戏，游戏规则是：一个不透明的文具袋中，装有型号完全相同的3支红笔和2支黑笔，两人先后从袋中取出一支笔（不放回），若两人所取笔的颜色相同，则小明胜，否则，小军胜．‎ ‎（1）请用树形图或列表法列出摸笔游戏所有可能的结果；‎ ‎（2）请计算小明获胜的概率，并指出本游戏规则是否公平，若不公平，你认为对谁有利．‎ 考点：‎ 游戏公平性；列表法与树状图法．菁优网版权所有 分析：‎ ‎（1）列表将所有等可能的结果一一列举出来即可；‎ ‎（2）根据列表里有概率公式求得小明获胜的概率即可判断是否公平．‎ 解答：‎ 解：（1）列表得：‎ 红1‎ 红2‎ 红3‎ 黑1‎ 黑2‎ 红1‎ 红1红2‎ 红1红3‎ 红1黑1‎ 红1黑2‎ 红2‎ 红2红1‎ 红2红3‎ 红2黑1‎ 红2黑2‎ 红3‎ 红3红1‎ 红3红2‎ 红3黑1‎ 红3黑2‎ 黑1‎ 黑1红1‎ 黑1红2‎ 黑1红3‎ 黑1黑2‎ 黑2‎ 黑2红1‎ 黑2红2‎ 黑2红3‎ 黑2黑1‎ ‎（2）共20种等可能的情况，其中颜色相同的有8种，‎ 则小明获胜的概率为=，‎ 小军获胜的概率为1﹣=，‎ ‎∵＜，‎ ‎∴不公平，对小军有利．‎ 点评：‎ 本题考查了列表法与列树状图的知识，解题的关键是正确的列出表格或树状图．‎ ‎　‎ ‎23．（10分）（2014•遵义）今年5月，从全国旅游景区质量等级评审会上传来喜讯，我市“风冈茶海之心”、“赤水佛光岩”、“仁怀中国酒文化城”三个景区加入国家“4A”级景区．至此，全市“4A”级景区已达13个．某旅游公司为了了解我市“4A”级景区的知名度情况，特对部分市民进行现场采访，根据市民对13个景区名字的回答情况，按答数多少分为熟悉（A），基本了解（B）、略有知晓（C）、知之甚少（D）四类进行统计，绘制了一下两幅统计图（不完整），请根据图中信息解答以下各题：‎ ‎（1）本次调查活动的样本容量是　1500　；‎ ‎（2）调查中属于“基本了解”的市民有　450　人；‎ ‎（3）补全条形统计图；‎ ‎（4）“略有知晓”类占扇形统计图的圆心角是多少度？“知之甚少”类市民占被调查人数的百分比是多少？‎ 考点：‎ 条形统计图；扇形统计图．菁优网版权所有 专题：‎ 图表型．‎ 分析：‎ ‎（1）用熟悉（A）的人数除以所占的百分比，计算即可得解；‎ ‎（2）先求出略有知晓（C）的人数，然后列式计算即可得解；‎ ‎（3）根据（2）的计算补全图形统计图即可；‎ ‎（4）用“略有知晓”C所占的百分比乘以360°计算即可，再根据知之甚少（D）的人数列式计算即可求出所占的百分比．‎ 解答：‎ 解：（1）120÷8%=1500；‎ ‎（2）略有知晓（C）的人数为：1500×40%=600人，‎ ‎“基本了解”（B）的人数为：1500﹣120﹣600﹣330=1500﹣1050=450人；‎ ‎（3）补全统计图如图所示；‎ ‎（4）“略有知晓”类：360°×40%=144°，‎ ‎“知之甚少”类：×100%=22%．‎ 故答案为：（1）1500；（2）450．‎ 点评：‎ 本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ ‎　‎ ‎24．（10分）（2014•遵义）如图，▱ABCD中，BD⊥AD，∠A=45°，E、F分别是AB，CD上的点，且BE=DF，连接EF交BD于O．‎ ‎（1）求证：BO=DO；‎ ‎（2）若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AD的长．‎ 考点：‎ 平行四边形的性质；全等三角形的判定与性质；等腰直角三角形．菁优网版权所有 分析：‎ ‎（1）通过证明△ODF与△OBE全等即可求得．‎ ‎（2）由△ADB是等腰直角三角形，得出∠A=45°，因为EF⊥AB，得出∠G=45°，所以△ODG与△DFG都是等腰直角三角形，从而求得DG的长和EF=2，然后平行线分线段成比例定理即可求得．‎ 解答：‎ ‎（1）证明：∵四边形ABCD是平行四边形，‎ ‎∴DC=AB，DC∥AB，‎ ‎∴∠ODF=∠OBE，‎ 在△ODF与△OBE中 ‎∴△ODF≌△OBE（AAS）‎ ‎∴BO=DO；‎ ‎（2）解：∵BD⊥AD，‎ ‎∴∠ADB=90°，‎ ‎∵∠A=45°，‎ ‎∴∠DBA=∠A=45°，‎ ‎∵EF⊥AB，‎ ‎∴∠G=∠A=45°，‎ ‎∴△ODG是等腰直角三角形，‎ ‎∵AB∥CD，EF⊥AB，‎ ‎∴DF⊥OG，‎ ‎∴OF=FG，△DFG是等腰直角三角形，‎ ‎∵△ODF≌△OBE（AAS）‎ ‎∴OE=OF，‎ ‎∴GF=OF=OE，‎ 即2FG=EF，‎ ‎∵△DFG是等腰直角三角形，‎ ‎∴DF=FG=1，‎ ‎∴DG==，‎ ‎∵AB∥CD，‎ ‎∴=，‎ 即=，‎ ‎∴AD=2，‎ 点评：‎ 本题考查了全等三角形的判定和性质，等腰直角三角形的判定和性质，平行线的性质以及平行线分行段定理．‎ ‎　‎ ‎25．（10分）（2014•遵义）为倡导低碳生活，绿色出行，某自行车俱乐部利用周末组织“远游骑行”活动．自行车队从甲地出发，途径乙地短暂休息完成补给后，继续骑行至目的地丙地，自行车队出发1小时后，恰有一辆邮政车从甲地出发，沿自行车队行进路线前往丙地，在丙地完成2小时装卸工作后按原路返回甲地，自行车队与邮政车行驶速度均保持不变，并且邮政车行驶速度是自行车队行驶速度的2.5倍，如图表示自行车队、邮政车离甲地的路程y（km）与自行车队离开甲地时间x（h）的函数关系图象，请根据图象提供的信息解答下列各题：‎ ‎（1）自行车队行驶的速度是　24　km/h；‎ ‎（2）邮政车出发多少小时与自行车队首次相遇？‎ ‎（3）邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远？‎ 考点：‎ 一次函数的应用．菁优网版权所有 分析：‎ ‎（1）由速度=路程÷时间就可以求出结论；‎ ‎（2）由自行车的速度就可以求出邮政车的速度，再由追击问题设邮政车出发a小时两车相遇建立方程求出其解即可；‎ ‎（3）由邮政车的速度可以求出B的坐标和C的坐标，由自行车的速度就可以D的坐标，由待定系数法就可以求出BC，ED的解析式就可以求出结论．‎ 解答：‎ 解：（1）由题意得 自行车队行驶的速度是：72÷3=24km/h．‎ 故答案为：24；‎ ‎（2）由题意得 邮政车的速度为：24×2.5=60km/h．‎ 设邮政车出发a小时两车相遇，由题意得 ‎24（a+1）=60a，‎ 解得：a=．‎ 答：邮政车出发小时与自行车队首次相遇；‎ ‎（3）由题意，得 邮政车到达丙地的时间为：135÷60=，‎ ‎∴邮政车从丙地出发的时间为：135=，‎ ‎∴B（，135），C（7.5，0）．‎ 自行车队到达丙地的时间为：135÷24+0.5=+0.5=，‎ ‎∴D（，135）．‎ 设BC的解析式为y1=k1+b1，由题意得 ‎，‎ ‎∴，‎ ‎∴y1=﹣60x+450，‎ 设ED的解析式为y2=k2x+b2，由题意得 ‎，‎ 解得：，‎ ‎∴y2=24x﹣12．‎ 当y1=y2时，‎ ‎﹣60x+450=24x﹣12，‎ 解得：x=5.5．‎ y1=﹣60×5.5+450=120．‎ 答：邮政车在返程途中与自行车队再次相遇时的地点距离甲地120km．‎ 点评：‎ 本题考查了行程问题的数量关系的运用，待定系数法求一次函数的解析式的运用，一次函数与一元一次方程的运用，解答时求出函数的解析式是关键．‎ ‎　‎ ‎26．（12分）（2014•遵义）如图，直角梯形ABCD中，AB∥CD，∠DAB=90°，且∠ABC=60°，AB=BC，△ACD的外接圆⊙O交BC于E点，连接DE并延长，交AC于P点，交AB延长线于F．‎ ‎（1）求证：CF=DB；‎ ‎（2）当AD=时，试求E点到CF的距离．‎ 考点：‎ 圆的综合题．菁优网版权所有 专题：‎ 综合题．‎ 分析：‎ ‎（1）连结AE，由∠ABC=60°，AB=BC可判断△ABC为等边三角形，由AB∥CD，∠DAB=90°得∠ADC=∠DAB=90°，则根据圆周角定理可得到AC为⊙O的直径，则∠AEC=90°，即AE⊥BC，根据等边三角形的性质得BE=CE，再证明△DCE≌△FBE，得到DE=FE，于是可判断四边形BDCF为平行四边形，根据平行四边形的性质得CF=DB；‎ ‎（2）作EH⊥CF于H，由△ABC为等边三角形得∠BAC=60°，则∠DAC=30°，在Rt△ADC中，根据含30度的直角三角形三边的关系得DC=AD=1，AC=2CD=2，‎ 则AB=AC=2，BF=CD=1，AF=3，然后利用勾股定理计算出BD=，DF=2，所以CF=BD=，EF=DF=，接着根据等边三角形的性质由AE⊥BC得∠CAE=∠BAE=30°，根据圆周角定理得∠EDC=∠CAE=30°，而∠DCA=∠BAC=60°，得到∠DPC=90°，在Rt△DPC中，根据含30度的直角三角形三边的关系得PC=DC=，‎ 再证明Rt△FHE∽Rt△FPC，利用相似比可计算出EH．‎ 解答：‎ ‎（1）证明：连结AE，如图，‎ ‎∵∠ABC=60°，AB=BC，‎ ‎∴△ABC为等边三角形，‎ ‎∵AB∥CD，∠DAB=90°，‎ ‎∴∠ADC=∠DAB=90°，‎ ‎∴AC为⊙O的直径，‎ ‎∴∠AEC=90°，即AE⊥BC，‎ ‎∴BE=CE，‎ CD∥BF，‎ ‎∴∠DCE=∠FBF，‎ 在△DCE和△FBE中，‎ ‎，‎ ‎∴△DCE≌△FBE（ASA），‎ ‎∴DE=FE，‎ ‎∴四边形BDCF为平行四边形，‎ ‎∴CF=DB；‎ ‎（2）解：作EH⊥CF于H，如图，‎ ‎∵△ABC为等边三角形，‎ ‎∴∠BAC=60°，‎ ‎∴∠DAC=30°，‎ 在Rt△ADC中，AD=，‎ ‎∴DC=AD=1，AC=2CD=2，‎ ‎∴AB=AC=2，BF=CD=1，‎ ‎∴AF=3，‎ 在Rt△ABD中，BD==，‎ 在Rt△ADF中，DF==2，‎ ‎∴CF=BD=，EF=DF=，‎ ‎∵AE⊥BC，‎ ‎∴∠CAE=∠BAE=30°，‎ ‎∴∠EDC=∠CAE=30°，‎ 而∠DCA=∠BAC=60°，‎ ‎∴∠DPC=90°，‎ 在Rt△DPC中，DC=1，∠CDP=30°，‎ ‎∴PC=DC=，‎ ‎∵∠HFE=∠PFC，‎ ‎∴Rt△FHE∽Rt△FPC，‎ ‎∴=，即=，‎ ‎∴EH=，‎ 即E点到CF的距离为．‎ 点评：‎ 本题考查了圆的综合题：熟练掌握圆周角定理、等边三角形的性质和平行四边形的判定与性质；会运用三角形全等的知识解决线段相等的问题；会运用勾股定理和相似比进行几何计算．‎ ‎　‎ ‎27．（14分）（2014•遵义）如图，二次函数y=x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0），与y轴交于点C．若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动．‎ ‎（1）求该二次函数的解析式及点C的坐标；‎ ‎（2）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由．‎ ‎（3）当P，Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状，并求出D点坐标．‎ 考点：‎ 二次函数综合题．菁优网版权所有 分析：‎ ‎（1）将A，B点坐标代入函数y=x2+bx+c中，求得b、c，进而可求解析式及C坐标．‎ ‎（2）等腰三角形有三种情况，AE=EQ，AQ=EQ，AE=AQ．借助垂直平分线，画圆易得E大致位置，设边长为x，表示其他边后利用勾股定理易得E坐标．‎ ‎（3）注意到P，Q运动速度相同，则△APQ运动时都为等腰三角形，又由A、D对称，则AP=DP，AQ=DQ，易得四边形四边都相等，即菱形．利用菱形对边平行且相等等性质可用t表示D点坐标，又D在E函数上，所以代入即可求t，进而D可表示．‎ 解答：‎ 解：（1）∵二次函数y=x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0），‎ ‎∴，‎ 解得 ，‎ ‎∴y=x2﹣x﹣4．‎ ‎∴C（0，﹣4）．‎ ‎（2）存在．‎ 如图1，过点Q作QD⊥OA于D，此时QD∥OC，‎ ‎∵A（3，0），B（﹣1，0），C（0，﹣4），O（0，0）‎ ‎∴AB=4，OA=3，OC=4，‎ ‎∴AC==5，AQ=4．‎ ‎∵QD∥OC，‎ ‎∴，‎ ‎∴，‎ ‎∴QD=，AD=．‎ ‎①作AQ的垂直平分线，交AO于E，此时AE=EQ，即△AEQ为等腰三角形，‎ 设AE=x，则EQ=x，DE=AD﹣AE=﹣x，‎ ‎∴在Rt△EDQ中，（﹣x）2+（）2=x2，解得 x=，‎ ‎∴OA﹣AE=3﹣=﹣，‎ ‎∴E（﹣，0）．‎ ‎②以Q为圆心，AQ长半径画圆，交x轴于E，此时QE=QA=4，‎ ‎∵ED=AD=，‎ ‎∴AE=，‎ ‎∴OA﹣AE=3﹣=﹣，‎ ‎∴E（﹣，0）．‎ ‎③当AE=AQ=4时，‎ ‎∵OA﹣AE=3﹣4=﹣1，‎ ‎∴E（﹣1，0）．‎ 综上所述，存在满足条件的点E，点E的坐标为（﹣，0）或（﹣，0）或（﹣1，0）．‎ ‎（3）四边形APDQ为菱形，D点坐标为（﹣，﹣）．理由如下：‎ 如图2，D点关于PQ与A点对称，过点Q作，FQ⊥AP于F，‎ ‎∵AP=AQ=t，AP=DP，AQ=DQ，‎ ‎∴AP=AQ=QD=DP，‎ ‎∴四边形AQDP为菱形，‎ ‎∵FQ∥OC，‎ ‎∴，‎ ‎∴，‎ ‎∴AF=，FQ=，‎ ‎∴Q（3﹣，﹣），‎ ‎∵DQ=AP=t，‎ ‎∴D（3﹣﹣t，﹣），‎ ‎∵D在二次函数y=x2﹣x﹣4上，‎ ‎∴﹣=（3﹣t）2﹣（3﹣t）﹣4，‎ ‎∴t=，或t=0（与A重合，舍去），‎ ‎∴D（﹣，﹣）．‎ 点评：‎ 本题考查了二次函数性质、利用勾股定理解直角三角形及菱形等知识，总体来说题意复杂但解答内容都很基础，是一道值得练习的题目．‎ ‎　‎