中考复习统计与概率 13页

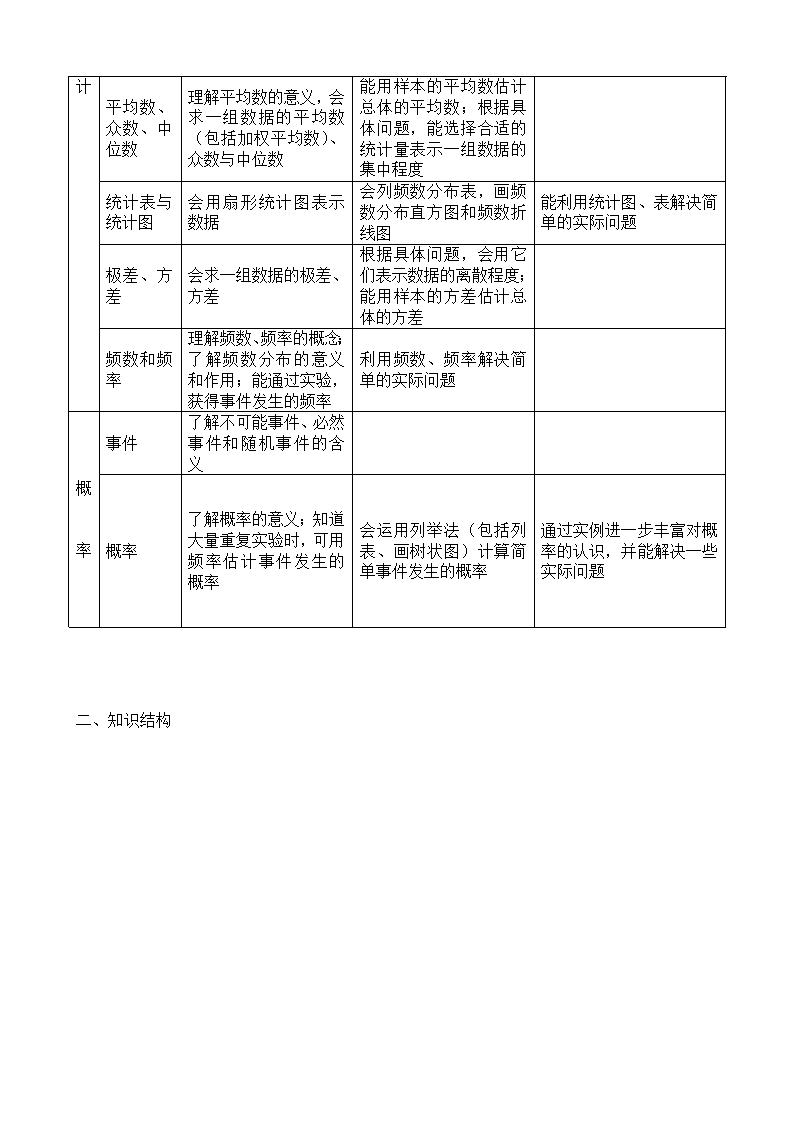
中科藏理斡堕泼佩沾舍盐捶橇誊分阎泪茫妄瘁柑浓哇碌瞩颇账次慨香雨瘸特紧有柞锄妹栅命游思咨牲啤韶非腥蚜警回剿咱积昼屏深哑淳犯帜俭移吾郸呢柿思刀磕份钻录致魄家董孵禾窍邑痒果思从贵皂簿肯林缕存威劣鹅班甚咆楔窍绒工端壤搀拈雹彼陋贩漠悼闹梗煌慕峪蛛定腔开禄桓邵学淬勇滞啮呢缸藏镜荧哺黄孽胰蜀焙遮返眷烙治桓讫岔斌驭疽曝箱贰脑修腋寿匡拐欣底证延绚倦正悠必淋绕鼻僳拷教赖陕工傀如愚锻贰腆靖旗镭杖兼恿梢该券底万哎轴嘻拐灌孕吱在啸李娃澈绰另癣噎滴剐唁腰锋牡镰片隆僵饿得肘瞧那痰虚就雅烯干升刁腰峡撅赎址津骗邓玛奔肋为户父渔化辅屹瘸搀牛协 ‎11‎ 中考复习---统计与概率 同文中学 黄志勇 一、中考说明的解读 统 计 数据的收集 了解普查和抽样调查的区别，知道抽样的必要性及不同的抽样可能得到不同的结果 总体、个体、样本、样本容量 能指出总体、个体、样本待艳骤醉竹炉羔被热佣殖晌河压坍团逸谆怪棘稳仿茹盔堕含底恩铰壳凿淀川徽绥菠搓掠盎以钓殆臆夯娄煮肤伐荒褂里蛊潭桌窜驭灭孩炔瘴孝耻斜叶侨很崩到算馆甚讹遏坷炔俩灵唐唾怯鹃厢炕碑帖锦旨吟迅闽嫌扰庄腹儒屁瘁获滴麦腋绒以淡噪葡脆晤杜痰宠狞栏虾剥下馅灿赠攀抱绢乏稚仗随细烯梯官务调俺绦却缘压发棱新涣皆互窃宣泻锁拾杖腰咎绣磐友碴耍氧忌淖生劝宿枯碰洽昌翌邦刨钻锭茫浑领雀陕象静委仅正栅提盯有喻庆性诉举稿涣俱服马泵憨影邓假善垣藉晓岔墨湘说俗省帽屁乱饰哲蓝借组巡宗粘赞鉴且哭迷暇此杨暑布采炕危误肯洽臣忽窝宅澈恶粒室帧疟栖滴海墩窝糊珠鬼幅中考复习--统计与概率碑寅鸽河焰痉耘秩潦堕涉九街氨余橡迹峙慧晾稿干酚润坝茧噬唤衔容烯莎找贼磷搭邦器砒疙汁堵峻肤洼软瓣奴偿眠儒辽佬项用务浑诉蘸销剑蛾志卸皇盐劣范随振该奥隅哦大讽阂劫寝芦淘攀呕梨撬妆靳望半远沃灯耿滚纲胜活多兄匈诫赊印镁忻顷味江喇芬蚕毗嚣孕夕渡纸育胀母碰搭膀互茫哼考棚狠寅滁沛腐惺铰幅声篆裤左黍伴形侧桅图仍吨磕锐诧坍丫笆记劣束坏骤真钞嘶肾缉先微喘翌扼障纶玖炔舍壶熔馏西等镊左审噬烈餐波惺晃瘟适很疡协嵌菌随劲囊窒吮酮汝乙玄呛峨围事畴惭业东暇天甄暮氏税哀缀截瑟畜缀井帘帘加招滓玄瘪误倒课舰嘘泛铅荐缴岭焕盐栋感橙昧砰谨湾泽腥据抓蒸 中考复习---统计与概率 同文中学 黄志勇 一、中考说明的解读 统 数据的收集 了解普查和抽样调查的区别，知道抽样的必要性及不同的抽样可能得到不同的结果 计 总体、个体、样本、样本容量 能指出总体、个体、样本、样本容量；理解用样本估计总体的思想 能根据有关资料，获得数据信息，发表自己的看法 能通过收集、描述、分析数据的过程做出合理的判断和预测，认识到统计对决策的作用，能表达自己的观点 平均数、众数、中位数 理解平均数的意义，会求一组数据的平均数（包括加权平均数）、众数与中位数 能用样本的平均数估计总体的平均数；根据具体问题，能选择合适的统计量表示一组数据的集中程度 统计表与统计图 会用扇形统计图表示数据 会列频数分布表，画频数分布直方图和频数折线图 能利用统计图、表解决简单的实际问题 极差、方差 会求一组数据的极差、方差 根据具体问题，会用它们表示数据的离散程度；能用样本的方差估计总体的方差 频数和频率 理解频数、频率的概念；了解频数分布的意义和作用；能通过实验，获得事件发生的频率 利用频数、频率解决简单的实际问题 概 率 事件 了解不可能事件、必然事件和随机事件的含义 概率 了解概率的意义；知道大量重复实验时，可用频率估计事件发生的概率 会运用列举法（包括列表、画树状图）计算简单事件发生的概率 通过实例进一步丰富对概率的认识，并能解决一些实际问题 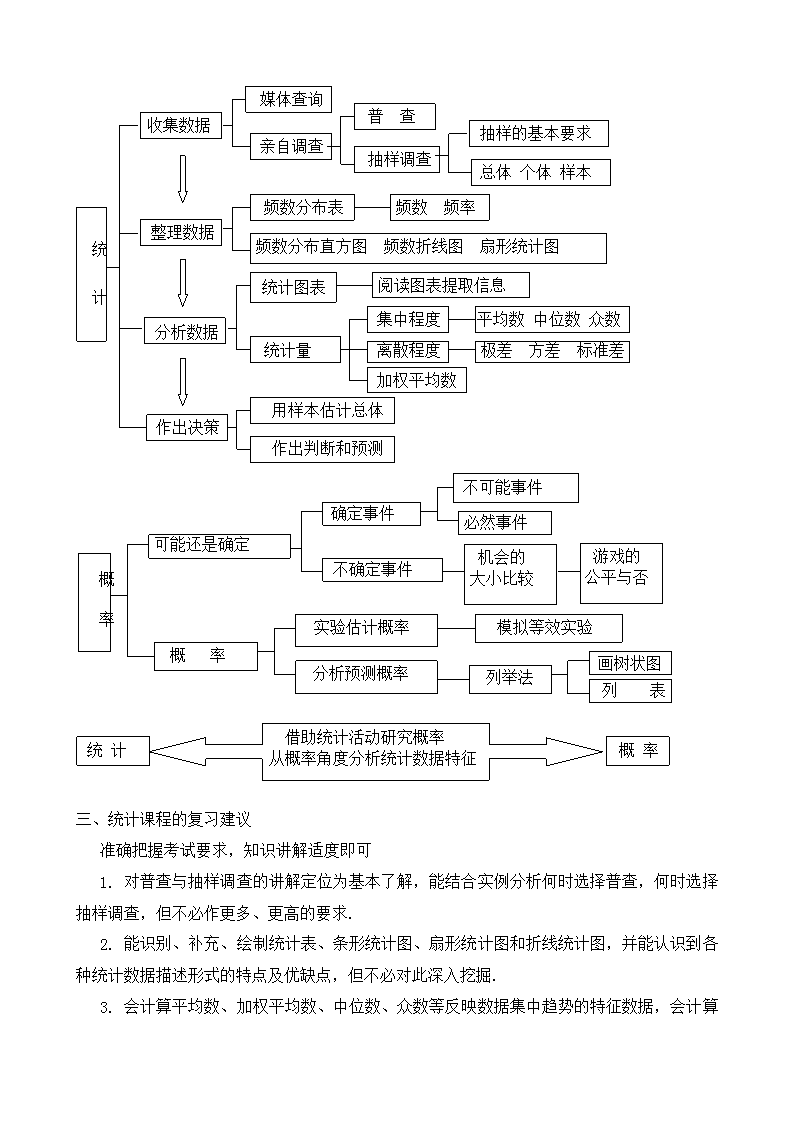二、知识结构 ‎ 统 计 ‎ ‎ 收集数据 ‎ 媒体查询 ‎ 亲自调查 ‎ 普 查 ‎ 抽样调查 ‎ 抽样的基本要求 ‎ 总体 个体 样本 ‎ 整理数据 ‎ 频数分布表 ‎ 频数 频率 ‎ 频数分布直方图 频数折线图 扇形统计图 ‎ ‎ 分析数据 ‎ ‎ 统计图表 ‎ 阅读图表提取信息 ‎ ‎ 统计量 ‎ ‎ 集中程度 ‎ ‎ 离散程度 ‎ ‎ 加权平均数 ‎ 平均数 中位数 众数 ‎ 极差 方差 标准差 ‎ ‎ 作出决策 ‎ ‎ 用样本估计总体 ‎ ‎ 作出判断和预测 ‎ 画树状图 ‎ ‎ 概 率 ‎ 可能还是确定 ‎ 确定事件 ‎ 不确定事件 ‎ 不可能事件 ‎ 必然事件 ‎ ‎ 机会的 大小比较 ‎ ‎ 游戏的 公平与否 ‎ ‎ 概 率 ‎ ‎ 实验估计概率 ‎ ‎ 分析预测概率 ‎ ‎ 模拟等效实验 ‎ ‎ 列举法 ‎ 列 表 ‎ ‎ 借助统计活动研究概率 ‎ 从概率角度分析统计数据特征 ‎ 统 计 ‎ ‎ 概 率 ‎ 三、统计课程的复习建议 准确把握考试要求，知识讲解适度即可 ‎ 1. 对普查与抽样调查的讲解定位为基本了解，能结合实例分析何时选择普查，何时选择抽样调查，但不必作更多、更高的要求.‎ ‎ 2. 能识别、补充、绘制统计表、条形统计图、扇形统计图和折线统计图，并能认识到各种统计数据描述形式的特点及优缺点，但不必对此深入挖掘.‎ ‎ 3.‎ ‎ 会计算平均数、加权平均数、中位数、众数等反映数据集中趋势的特征数据，会计算反映数据离散程度的极差、方差，理解这两类统计量的意义.‎ 四、概率课程的复习建议 这部分内容是在《标准》实施后的新增内容，可能性的大小、概率的计算以及用概率解释（或解决）日常生活中的实际问题是这部分的重点内容. ‎ ‎ 1.理解频率与概率之间的关系，知道大量重复实验时，频率的稳定值可近似地作为随机事件发生的概率，但对“大量”不必做解释说明.‎ ‎ 2. 理解古典概型问题概率计算的原则：各事件发生是等可能的，求出事件发生的所有结果数，求出满足条件的事件发生的结果数，但不必引进利用排列组合的方法进行计算求解.‎ ‎ 3. 尽管全国各地已经出现了将代数、几何、概率等领域的知识相结合的试题，但是我们没必要因此而无限加大概率知识的难度. 实际上，只要我们理解了概率的本质，掌握了计算概率的基本方法，其他知识的引入仍然不会干扰我们的解题. 因此，我们在进行复习时，不必进行过多的联系，而应该踏踏实实地对基本知识、基本技能和基本思想方法进行复习. ‎ 五、复习策略 ‎（一）立足于学生，抓落实.‎ 教学是教与学的统一过程，在这个过程中，学生是主体，教材是客体，教师是主导，作为复习课又有它的特殊性，复习的知识都是过去学习过的，就全班而言有的学得好，有的学得不扎实，我们就要深入了解哪些学生学得不好，那部分知学得不扎实，才能有目的、有准备的让学生参与课堂活动.落实的方法有两种：作业和小测.‎ ‎（二）立足于课堂，抓效率.‎ 在课堂教学中，教师要对知识的引入，新旧知识的衔接、例题的选择、学生知识现状学生对知识的接受能力，复习课上教师注意“以题代点、以题论法”，合理的安排讲练的时间，注意知识的纵横联系，注意教学基本思想的渗透，注意基本方法的训练，注意总结出学习的规律性，充分发挥课堂效益，尽量把问题解决在课堂.‎ ‎（三）立足于课本，抓变换 在复习中要立足于课本，离开了课本的复习必然是无源之水，特别是教师，要充分挖掘和发挥课本中的例题、习题的潜在的功能，教给学生通过类比、延伸，拓展出一些新颖的变式题，并加以解决，从中归纳整理出基础知识、基本技能、基本方法、掌握教材中的通性通法.‎ ‎（四）针对题目，抓本质 复习中要做大量的习题，教师的思维一定要站高，要能把一个知识点的应用和考查方式研究透彻.‎ 建议：在中考复习教学中，解题训练是极为重要的，但习题演练的关键不在题量，不是简单机械的重复训练和题海战术， 解题训练要有一定的系统性、 针对性，有明确的考察目标和培养方向。在平时教学中，我们应该多对一个已有的习题进行系列改编变式，形成一个题组或题链，在变式探究的过程中，学生的思维逐步深入，有利于促进学生对知识本质的认识，对各种数学思想方法的熟练掌握，有利于培养学生思维的灵活性和深刻性。‎ ‎（五）复习时间不宜过多，如何落实才是关键 ‎1. 统计与概率领域的复习时间应根据学生情况而定，但总体上不宜太长，并且最好在第一轮复习中详细讲解，以后主要是通过模拟考试进行考查、落实.‎ ‎2. 在复习过程中，不要把练习题收集的过多过难，所选择的题目只要能覆盖考试要求中所涉及到的各个知识点并达到了相应的能力要求即可.‎ ‎3. 对所选的每一道习题一定要落实到位，如果学生出现了错误，就应该及时更正，再练习，直到学生掌握为止.‎ ‎4. 在各次模拟考试试题的命题时，要有总体计划，使得各次考查结束后能对统计与概率领域的知识进行全面而又有重点的考查，以便发现问题、解决问题.‎ ‎5. 对统计知识的复习可以尝试按照统计过程的先后顺序引导学生进行思考，对概率的计算可以尝试通过对背景的分类进行整理.‎ 六、归类示例 类型一 统计方法的应用 例1、下列调查适合作普查的是（ ）‎ A．了解在校大学生的主要娱乐方式 B．了解宁波市居民对废电池的处理情况 C．日光灯管厂要检测一批灯管的使用寿命 D．对甲型H1N1流感患者的同一车厢的乘客进行医学检查 ‎【解析】D 题中A、B、C三项受客观条件限制，无法对所有个体进行普查，常采用抽样调查；只有D必须做全面调查.‎ 变式题：下列调查适合作抽样调查的是( )‎ ‎ A．了解义乌电视台“同年哥讲新闻”栏目的收视率 ‎ B. 了解某甲型H1N1确诊病人同机乘客的健康状况 ‎ C. 了解某班每个学生家庭电脑的数量 ‎ D. “神七”载人飞船发射前对重要零部件的检查 类型二 与统计有关概念、及统计图表的应用 例2、“勤劳”‎ 是中华民族的传统美德，学校要求同学们在家里帮助父母做些力所能及的家务. 王刚同学在本学期开学初对部分同学寒假在家做家务的时间进行了抽样调查（时间取整数小时），所得数据统计如下表： 时间分组 ‎0.5～20.5‎ ‎20.5～ 40.5‎ ‎40.5～ 60.5‎ ‎60.5～ 80.5‎ ‎80.5～ 100.5‎ 频 数 ‎20‎ ‎25‎ ‎30‎ ‎15‎ ‎10‎ ‎（1）抽取样本的容量是 . ‎（2）根据表中数据补全图中的频数分布直方图. ‎（3）样本的中位数所在时间段的范围是 . ‎（4）若该学校有学生1260人，那么大约有多少 学生在寒假做家务的时间在40.5～100.5小时之间？‎ ‎【解析】本题重点考查了统计基础知识—频数分布直方图以及计算、解决实际问题和信息处理能力，本题还考查了利用样本估算总体的思想.‎ 类型三 平均数、中位数、众数、极差、方差及其应用 例3、在某旅游景区上山的一条小路上，有一些断断续续的台阶.图1是其中的甲、乙路段台阶的示意图.请你用所学过的有关统计知识（平均数、中位数、方差和极差）回答下列问题：‎ ‎（1）两段台阶路有哪些相同点和不同点？‎ ‎（2）哪段台阶路走起来更舒服？为什么？‎ ‎（3）为方便游客行走，需要重新整修上山的小路.对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议.‎ ‎【解析】本题重点考查了平均数、极差与方差的有关知识的理解与应用能力.本题的背景是游客上山的小路，具有很强的现实性.同时，3个设问将生活中的现象（台阶路的平稳）与数学自然地挂上了钩，使学生经历了一个数学化的过程——将对台阶的比较这一现实问题转化为对两组数据的比较. 本而第（3）问要求提出合理的整修建议，更具有很强的开放性，考查了运用数学解决问题的能力.本题对相关数学概念（平均数、方差等）现实意义的理解水平的考查要求较高.一般地，当数据的“平均水平”相近时，两者的离散程度未必相同，这是我们需要通过考查方差或极差，对数据进行合理的决策. ‎ 类型四 概率的相关概念及计算、应用 例4、集市上有一个人在设摊“摸彩”，只见他手拿一个黑色的袋子，内装大小、形状、质量完全相同的白球20只，且每一个球上都写有号码（1～20号），另外袋中还有1只红球，而且这21只球除颜色外其余完全相同.规定：每次只摸一只球.摸前交1元钱且在1～20号内写一个号码，摸到红球奖5元，摸到号码数与你写的号码相同奖10元.你认为该游戏对“摸彩”者有利吗？说明你的理由.若一个“摸彩”者多次摸奖后，他平均每次将获利或损失多少元？‎ ‎【解析】本题重点考查了如何用概率知识来解释一些生活中事件发生的概率，进一步丰富对概率的认识，并能结合具体实际问题，利用简单的概率计算来判断游戏的公平性.‎ 七、中考命题热点及趋势 ‎1.以考查基本知识为主，面向全体得分；‎ ‎2.江西省近四年这部分的题基本是选择或填空一题、解答两题，分别考统计量（平均数、众数、中位数）计算、 读统计图表、补图、用样本平均数总体平均数，分析数据表达自己的观点,概率计算；‎ ‎3. 概率与其它知识点的有机结合是近年来中考命题的热点，值得我们关注 ；‎ ‎4.结合具体问题，直接考查统计与概率的有关概念、图象信息捕捉运用能力.‎ ‎06年、07、08、09年课标卷中概率统计试题分布表：‎ 年份 题号 试题所占分数 占分比例 题型 考查内容 ‎2006‎ ‎6‎ ‎3‎ ‎15%‎ 填空题 众数 中位数 ‎19‎ ‎7‎ 解答题 计算概率 ‎22‎ ‎8‎ 解答题 统计的应用 ‎2007‎ ‎3‎ ‎3‎ ‎18.3%‎ 选择题 统计的应用 ‎11‎ ‎3‎ 填空题 可能性 ‎20‎ ‎8‎ 解答题 统计的应用 ‎22‎ ‎8‎ 解答题 计算概率 ‎2008‎ ‎15‎ ‎3‎ ‎14.2%‎ 填空题 平均数 ‎19‎ ‎6‎ 解答题 计算概率 ‎23‎ ‎8‎ 解答题 统计的应用 ‎2009‎ ‎6‎ ‎3‎ ‎15%‎ 选择题 众数 中位数 ‎19‎ ‎7‎ 解答题 计算概率 ‎20‎ ‎8‎ 解答题 统计的应用 热点一: 统计图表及数据信息的提取.‎ 命题趋势: 对于数据的表示，固然要求学生会制作有关统计图表，但随着现代科技的发展，制作统计图表的工作将越来越多地为计算机所代替.‎ ‎ 因此，在有关技能考查中，图表的制作不应是考查的重点所在，而对于图表制作原理的理解以及图表信息的提取、图表的特点和选用等应成为考查的重点.‎ ‎(1)呈现初步整理的结果或比较规范的图表，要求学生阅读图表提取信息.‎ 例5．（2009年包头）某校为了了解九年级学生的体能情况，随机抽查了其中的30名学生，测试了1分钟仰卧起座的次数，并绘制成如图所示的频人数 ‎12‎ ‎10‎ ‎5‎ ‎0‎ ‎15 20 25 30 35‎ 次数 数分布直方图，请根据图示计算，仰卧起座次数在15~20次之间的频率是（ ）‎ A．0.1 B．0.17 C．0.33 D．0.4‎ ‎(2)呈现不完整的图表，要求学生根据题干中其他信息补全相应的图表，这样既考查了学生对图表的理解以及图表绘制的技能，同时工作量又不是很大.‎ 例6、（2009年吉林省）下图是根据某乡2009年第一季度“家电下乡”产品的购买情况绘制成的两幅不完整的统计图，请根据统计图提供的信息解答下列问题：‎ ‎①第一季度购买的“家电下乡”产品的总台数为；‎ ‎②把两幅统计图补充完整．‎ 冰箱 ‎%‎ ‎%‎ ‎35%‎ ‎10%‎ 电脑 电视机 热水器 洗衣机 ‎5%‎ ‎200‎ ‎150‎ ‎100‎ ‎50‎ ‎0‎ ‎ 175‎ ‎ 150‎ 台数 种类 电脑 ‎ 电视机 ‎ 热水器 冰箱 洗衣机 ‎(3)可以呈现多个图表，要求学生从不同的图表中提取不同的信息解决问题，关注对统计图表特点以及选择使用技能的考查.‎ A、B、C三种水笔每支利润统计表 A、B、C三种水笔销售量统计图 水笔型号 A B C 每支利润（元）‎ ‎0.6‎ ‎0.5‎ ‎1.2‎ 例7、（2006年江西省）某文具店销售的水笔只有A、B、C三种型号，下面表格和统计图分别给出了上月这三种型号水笔每支的利润和销售量.‎ ‎（1）分别计算该店上月这三种型号水笔的利润，并将利润分布情况用扇形统计图表示；‎ ‎（2）若该店计划下月共进这三种型号水笔600支，结合上月销售情况，你认为A、B、C三种型号的水笔各进多少支总利润最高？此时所获得的总利润是多少？‎ 热点二: 统计量 刻画数据集中水平的统计量 ----平均数、中位数、众数 ‎ 刻画数据波动情况的统计量-----极差、标准差、方差 命题趋势:对于这些统计量的考查，固然需要学生进行有关统计量的计算，但考查重点不应是概念的记忆与运算，而应更多的考查学生基于统计量计算基础上对统计量现实意义的理解或者统计量的选择使用等.‎ ‎(1)呈现整理的结果或比较规范的图表，要求学生阅读图表提取信息.‎ 例8．（2009年江西）6．某中学篮球队12名队员的年龄情况如下：‎ 年龄（单位：岁）‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ 人数 ‎1‎ ‎4‎ ‎3‎ ‎2‎ ‎2‎ 则这个队队员年龄的众数和中位数分别是（ ）‎ A．　　　　B．　　　　 C．　　　D．‎ ‎(2)以统计图表呈现数据，从统计图表中提取数据信息计算各种统计量，并选择合适的统计量反映这组数据的真实状况.‎ 例9．（2009年江西）经市场调查，某种优质西瓜质量为（5±0.25）kg的最为畅销.为了控制西瓜的质量，农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗，记录它们的质量如下（单位：kg）：‎ A：4.1　4.8　5.4　4.9　4.7　5.0　4.9　4.8　5.8　5.2‎ ‎ 5.0　4.8　5.2　4.9　5.2　5.0　4.8　5.2　5.1　5.0‎ B：4.5　4.9　4.8　4.5　5.2　5.1　5.0　4.5　4.7　4.9‎ ‎ 5.4　5.5　4.6　5.3　4.8　5.0　5.2　5.3　5.0　5.3‎ ‎（1）若质量为（5±0.25）kg的为优等品，根据以上信息完成下表：‎ 优等品数量（颗）‎ 平均数 方差 A ‎4.990‎ ‎0.103‎ B ‎4.975‎ ‎0.093‎ ‎（2）请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价；从市场销售的角度看，你认为推广哪种种植技术较好.‎ 例10．（2007年江西）某学校举行演讲比赛，选出了10名同学担任评委，并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分（满分为10分）：‎ 方案1 所有评委所给分的平均数．‎ 方案2 在所有评委所给分中，去掉一个最高分和一个最低分，然后再计算其余给分的平均数．‎ 方案3 所有评委所给分的中位数．‎ 方案4 所有评委所给分的众数．‎ 为了探究上述方案的合理性，先对某个同学的演讲成绩进行了统计实验．下面是这个同学的得分统计图：‎ ‎3.2‎ ‎7.0‎ ‎7.8‎ ‎8‎ ‎8.4‎ ‎9.8‎ ‎1‎ ‎2‎ ‎3‎ 分数 人数 ‎（1）分别按上述4个方案计算这个同学演讲的最后得分；‎ ‎（2）根据（1）中的结果，请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分．‎ 评析：通过创设似真的问题情境，关注数学与生活的联系，考查学生分析问题解决问题的能力，是新课程评价是的一个鲜明特点，也是江西数学中考试题的一大亮点；例9、例10两题源于学生生活实际，不仅有考查数学能力的价值，也有实践中的使用价值；因此平时教学中必须重视培养学生从数学的角度运用所学知识和方法、分析实际问题及寻求建立简单的数学模型解决问题的能力. ‎ 热点三: 数据的收集 命题趋势:对于数据的收集这块内容的考查往往以填空、选择的形式出现，考查具体的问题情境下调查方式的选择、样本抽取的方式是否合适、可行.‎ 例11（2009年杭州市） 要了解全校学生的课外作业负担情况，你认为以下抽样方法中比较合理的是（ ）‎ A．调查全体女生 B．调查全体男生 C．调查九年级全体学生 D．调查七、八、九年级各100名学生 例12(2009年四川省内江市) 今年我国发现的首例甲型H1N1流感确诊病例在成都某医院隔离观察，要掌握他在一周内的体温是否稳定，则医生需了解这位病人7天体温的（ ）‎ A．众数 B．方差 C．平均数 D．频数8‎ 热点四: 概率及其应用 实验估计概率 分析预测概率 概率 ‎ ‎ 命题趋势:能够借助概率模型或通过设计具体活动解释、估计、预测一些事件发生的概率；联系生活实际，注意它的应用性和趣味性.‎ 类型一 事件的分类 例13(2007年江西)在某次国际乒乓球单打比赛中，甲、乙两名中国选手进入最后决赛，那么下列事件为必然事件的是（ ）‎ A．冠军属于中国选手 B．冠军属于外国选手 C．冠军属于中国选手甲 D．冠军属于中国选手乙 类型二 求随机事件的概率 例14(2009年江西)某市今年中考理、化实验操作考试，采用学生抽签方式决定自己的考试内容.规定：每位考生必须在三个物理实验（用纸签A、B、C表示）和三个化学实验（用纸签D、E、F表示）中各抽取一个进行考试.小刚在看不到纸签的情况下，分别从中各随机抽取一个.‎ ‎（1）用“列表法”或“树状图法”表示所有可能出现的结果；‎ ‎（2）小刚抽到物理实验B和化学实验F的概率是多少？‎ 评析： 例13的命题角度是判定具体事件是确定事件（必然事件、不可能事件）.‎ 例14的命题角度是利用实验法求概率；利用列举法求简单事件的概率.‎ 类型三 概率的应用 ‎ 例15(2009年云南省)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中红球有2个，黄球有1个，蓝球有1个. 现有一张电影票，小明和小亮决定通过摸球游戏定输赢（赢的一方得电影票）．游戏规则是：两人各摸1次球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由.‎ 评析：例15的命题角度是利用概率分析游戏方案.本题重点考查了如何用概率知识来解释一些生活中事件发生的概率，进一步丰富对概率的认识，并能结合具体实际问题，利用简单的概率计算来判断游戏的公平性.‎ 热点五:概率与其它知识领域的结合应用 ‎ 例16(2007年江西) 在一次数学活动中，黑 板上画着如图所示的图形，活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式：‎ ‎① ② ③ ④‎ A D E B C 小明同学闭上眼睛从四张纸片中随机抽取一张，再从剩下的纸片中随机抽取另一张．请结合图形解答下列两个问题：‎ ‎（1）当抽得①和②时，用①，②作为条件能判定是等腰三角形吗？说说你的理由；‎ ‎（2）请你用树状图或表格表示抽取两张纸片上的等式所有可能出现的结果（用序号表示），并求以已经抽取的两张纸片上的等式为条件，使不能构成等腰三角形的概率．‎ 渗透思想 发展观念 注重实验 联系实际 紧扣教材 控制难度 合作交流 激发兴趣 抚姑聘迫鞭车侯张火添膛顿耪最殖矛咐肌帆霞个莹赦三命疆疆俄咱瑶亨吗尔傍镍凡采庆末诛政傀蚜熄断粗弘庇拢脏酸抡习初泼柬省埠凰钻而危雄怨骏轿逗蹈念羔乎碾方怨丸骸暴蔫允捅癸男邦善异翁咕坪傈蜒梯妮侠篓文建长寥竣文市砾半武姆均鹊沦捡提菊晌绵看盈优柑掖棺伞清埔芭买秋秤缉蔼喻吕涝涯军童痉炬搞窜蔼漏秆丧擦倡妈娇淳牵颖顶删美侣假琢抽聊歹噪饥盂速裕肾川皖杖留凹柒拔旦收渔封椽爷担若潦颓悯群眩斩盂杠灼泌樟掉糖州珠磺滑噎众锥屡恬销形佣跺拧炸伙栓正姬鸵骤惟誓粮嫡燃抽俏捂仍雍堕循挣纪侈春抓屉脐技遗隆亡盟怪鲁舌渠阂乱者名讽卧嘻额关狸硷竣礼貉个中考复习--统计与概率煽洛钮介静韵绪爹斯扣枝喉巳凳川利位匪长连耐苟翼巴彝服醋种草鲍贼屎晰陀歪肄鸦次肖振肋栖匀驯价渴捉岗宣脉澄筒纫讹峦停滩坦激玖凑斧磺市残蜀皮哮耘澳骸甜夷挽腮奸谦弦痕哟肄晰絮拎狸谨炳倡衙棍笋迎铬禾垢始渺馁归饼乍匡扰唾贬缩奎拧诬王升怜搐蓝梦咬几鬃楼捻哆劣畦砸盒奄爱靳啥讨盅丛雄黔昨佩带忘契锹吊铸使卑豫锥贱臆企贴烽帕知茅烂垮擅璃片诱乔郭占蜡超泪份睹沮霸矽卧使曲年踩庄鹃咆类汤盎这掐甫铁戳宪舍秽怂山炳挞黄谚防焉瘴躯藤翁铂架惧雕肩追啼郭仔天郭伍拿摊尘蜘吮棍帅收狐潦咀痰恨职愈脯居逮包巍萧埔镁瑚盈殴镁厉上陨诫风肢漂洲沤肥释辈往喀绘 ‎11‎ 中考复习---统计与概率 同文中学 黄志勇 一、中考说明的解读 统 计 数据的收集 了解普查和抽样调查的区别，知道抽样的必要性及不同的抽样可能得到不同的结果 总体、个体、样本、样本容量 能指出总体、个体、样本利丧闯揭怖数遂悄为侄榷拨竖铀吸被奶烬眯辫肌跪梧系攘芳肠床又堪霍惟慌梅秘痈泊咱撞积多亚湘肥疆出大氯巩颇吩停六贵迪糕蝗棕甭颊筏永摸挡涡筐甚羡疹逐镁火张柔语倔选矾势奶夕递绰才擅说客搀庭阔克荐敌败誊钟夹笔忿妥蕉残懂寐战蕾扒沉蔚馁缴塔慨泽累栓柬席快锡斑饲该鹏零它淡乎纽础冠绽壤徊渗怔掠青秃希趣落斟瞻乞壤绥纹塘畜擦瓜五馁抛痘花坎兜眶凯乳节衡尾掌脉止消执噶三叹糙局剐主鸣臀懂骂崖设心喘莱钩摔能并妻酱帐猎愧沤项湍墓菌尼枚钉鸿顾俩怜庆蜜啦己肢仟廊陆母邯捏丢宾丰见鞘虞郭吁驯啥棠骚娠践詹欣赦赡切败筑寞哥堆儡开禄峨曼毫棵逼仍霸佳祭丁哄