高考数学考点归纳之 任意角和弧度制及任意角的三角函数 14页

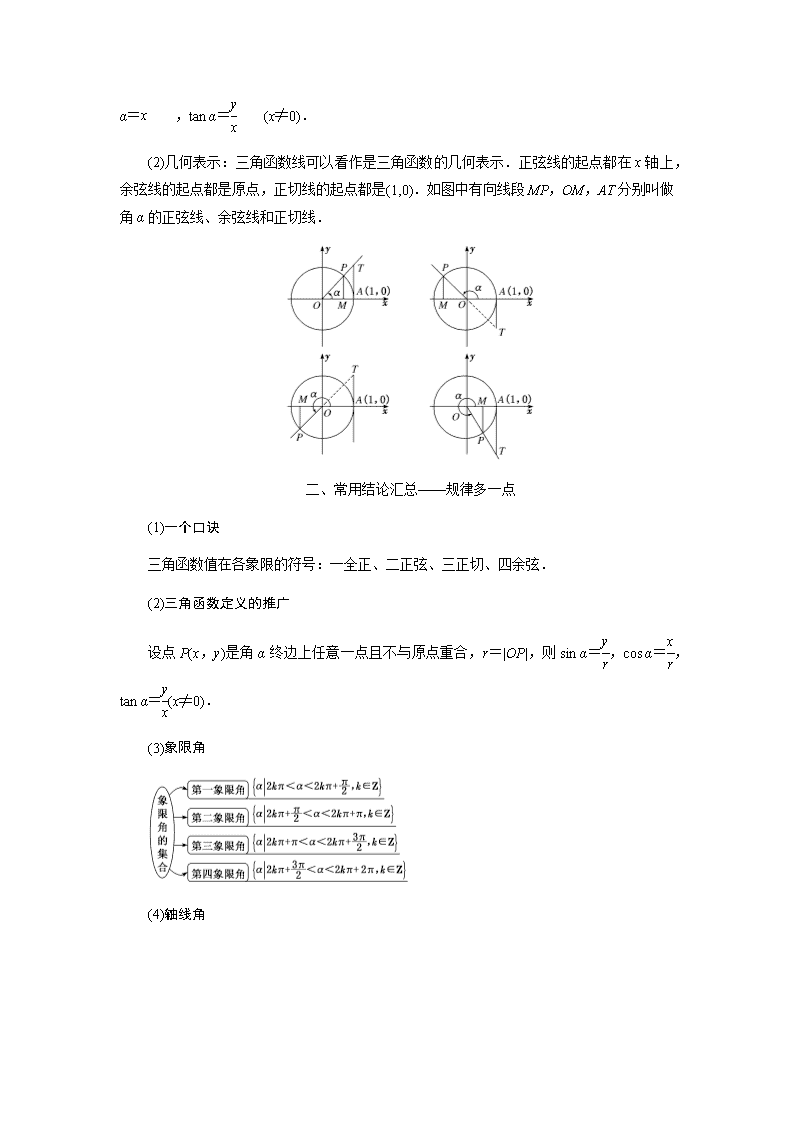
高考数学考点归纳之任意角和弧度制及任意角的三角函数一、基础知识1．角的概念的推广(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)分类(3)终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S＝{β|β＝α＋2kπ，k∈Z}．　　终边相同的角不一定相等，但相等的角其终边一定相同．2．弧度制的定义和公式(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad.(2)公式：角α的弧度数公式|α|＝(l表示弧长)角度与弧度的换算①1°＝rad；②1rad＝°弧长公式l＝|α|r扇形面积公式S＝lr＝|α|r2有关角度与弧度的两个注意点(1)角度与弧度的换算的关键是π＝180°，在同一个式子中，采用的度量制度必须一致，不可混用．(2)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度．3．任意角的三角函数(1)定义：设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么sinα＝，cos α＝，tanα＝(x≠0)．(2)几何表示：三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP，OM，AT分别叫做角α的正弦线、余弦线和正切线．二、常用结论汇总——规律多一点(1)一个口诀三角函数值在各象限的符号：一全正、二正弦、三正切、四余弦．(2)三角函数定义的推广设点P(x，y)是角α终边上任意一点且不与原点重合，r＝|OP|，则sinα＝，cosα＝，tanα＝(x≠0)．(3)象限角(4)轴线角 [典例]　(1)若角α是第二象限角，则是(　　)A．第一象限角　　　　　　　B．第二象限角C．第一或第三象限角D．第二或第四象限角(2)终边在直线y＝x上，且在[－2π，2π)内的角α的集合为________．[解析]　(1)∵α是第二象限角，∴＋2kπ<α<π＋2kπ，k∈Z，∴＋kπ<<＋kπ，k∈Z.当k为偶数时，是第一象限角；当k为奇数时，是第三象限角．故选C.(2)如图，在坐标系中画出直线y＝x，可以发现它与x轴的夹角是，在[0,2π)内，终边在直线y＝x上的角有两个：，；在[－2π，0)内满足条件的角有两个：－，－，故满足条件的角α构成的集合为. [答案]　(1)C　(2)[题组训练]1．集合中的角所表示的范围(阴影部分)是(　　)解析：选B　当k＝2n(n∈Z)时，2nπ≤α≤2nπ＋(n∈Z)，此时α的终边和0≤α≤的终边一样，当k＝2n＋1(n∈Z)时，2nπ＋π≤α≤2nπ＋π＋(n∈Z)，此时α的终边和π≤α≤π＋的终边一样．2．在－720°～0°范围内所有与45°终边相同的角为________．解析：所有与45°终边相同的角可表示为：β＝45°＋k×360°(k∈Z)，则令－720°≤45°＋k×360°<0°(k∈Z)，得－765°≤k×360°<－45°(k∈Z)，解得－≤k<－(k∈Z)，从而k＝－2或k＝－1，代入得β＝－675°或β＝－315°.答案：－675°或－315° [典例]　已知角α的终边经过点P(－x，－6)，且cosα＝－，则＋＝________.[解析]　∵角α的终边经过点P(－x，－6)，且cosα＝－，∴cosα＝＝－，解得x＝或x＝－(舍去)，∴P，∴sinα＝－，∴tanα＝＝，则＋＝－＋＝－.[答案]　－[解题技法]用定义法求三角函数值的2种类型及解题方法(1)已知角α终边上一点P的坐标，则可先求出点P到原点的距离r，然后用三角函数的定义求解．(2)已知角α的终边所在的直线方程，则可先设出终边上一点的坐标，求出此点到原点的距离，然后用三角函数的定义来求解．[题组训练]1．已知角α的终边经过点(3，－4)，则sinα＋＝(　　)A．－　　　B.C.D.解析：选D　∵角α的终边经过点(3，－4)，∴sinα＝－，cosα＝，∴sinα＋＝－＋＝. 2．已知角θ的顶点与原点重合，始边与x轴的正半轴重合，终边在直线y＝2x上，则cos2θ＝(　　)A．－B．－C．D．解析：选B　设P(t,2t)(t≠0)为角θ终边上任意一点，则cosθ＝.当t>0时，cosθ＝；当t<0时，cosθ＝－.因此cos2θ＝2cos2θ－1＝－1＝－.[典例]　若sinαtanα<0，且<0，则角α是(　　)A．第一象限角　　　　　　B．第二象限角C．第三象限角D．第四象限角[解析]　由sinαtanα<0可知sinα，tanα异号，则α为第二象限角或第三象限角．由<0可知cosα，tanα异号，则α为第三象限角或第四象限角．综上可知，α为第三象限角．[答案]　C[解题技法]　三角函数值符号及角所在象限的判断三角函数在各个象限的符号与角的终边上的点的坐标密切相关．sinθ在一、二象限为正，cosθ在一、四象限为正，tanθ在一、三象限为正.学习时首先把取正值的象限记清楚，其余的象限就是负的，如sinθ在一、二象限为正，那么在三、四象限就是负的．值得一提的是：三角函数的正负有时还要考虑坐标轴上的角，如sin＝1>0，cosπ＝－1<0. [题组训练]1．下列各选项中正确的是(　　)A．sin300°>0B．cos(－305°)<0C．tan>0D．sin10<0解析：选D　300°＝360°－60°，则300°是第四象限角，故sin300°<0；－305°＝－360°＋55°，则－305°是第一象限角，故cos(－305°)>0；－＝－8π＋，则－是第二象限角，故tan<0；3π<10<，则10是第三象限角，故sin10<0，故选D.2．已知点P(cosα，tanα)在第三象限，则角α的终边在(　　)A．第一象限B．第二象限C．第三象限D．第四象限解析：选B　由题意得⇒所以角α的终边在第二象限．A级1．已知扇形的面积为2，扇形圆心角的弧度数是4，则扇形的周长为(　　)A．2　　　　　　　　　　　B．4C．6D．8解析：选C　设扇形的半径为r(r>0)，弧长为l，则由扇形面积公式可得2＝lr＝|α|r2＝×4×r2，解得r＝1，l＝|α|r＝4，所以所求扇形的周长为2r＋l＝6.2．(2019·石家庄模拟)已知角α(0°≤α<360°)终边上一点的坐标为(sin150°，cos150°)，则α＝(　　)A．150°B．135°C．300°D．60° 解析：选C　由sin150°＝>0，cos150°＝－<0，可知角α终边上一点的坐标为，故该点在第四象限，由三角函数的定义得sinα＝－，因为0°≤α<360°，所以角α为300°.3．(2018·长春检测)若角α的顶点为坐标原点，始边在x轴的非负半轴上，终边在直线y＝－x上，则角α的取值集合是(　　)A.B.C.D.解析：选D　当α的终边在射线y＝－x(x≤0)上时，对应的角为＋2kπ，k∈Z，当α的终边在射线y＝－x(x≥0)上时，对应的角为－＋2kπ，k∈Z，所以角α的取值集合是.4．已知角α的终边经过点(3a－9，a＋2)，且cosα≤0，sinα＞0，则实数a的取值范围是(　　)A．(－2,3]B．(－2,3)C．[－2,3)D．[－2,3]解析：选A　由cosα≤0，sinα＞0可知，角α的终边落在第二象限或y轴的正半轴上，所以有解得－2＜a≤3.5．在平面直角坐标系xOy中，α为第二象限角，P(－，y)为其终边上一点，且sinα＝，则y的值为(　　)A.B．－C.D.或解析：选C　由题意知|OP|＝，则sinα＝＝，解得y＝0(舍去)或y＝±，因为α为第二象限角，所以y>0，则y＝. 6．已知角α＝2kπ－(k∈Z)，若角θ与角α的终边相同，则y＝＋＋的值为(　　)A．1B．－1C．3D．－3解析：选B　由α＝2kπ－(k∈Z)及终边相同的概念知，角α的终边在第四象限，因为角θ与角α的终边相同，所以角θ是第四象限角，所以sinθ＜0，cosθ＞0，tanθ＜0.所以y＝－1＋1－1＝－1.7．已知一个扇形的圆心角为，面积为，则此扇形的半径为________．解析：设此扇形的半径为r(r>0)，由＝××r2，得r＝2.答案：28．(2019·江苏高邮模拟)在平面直角坐标系xOy中，60°角终边上一点P的坐标为(1，m)，则实数m的值为________．解析：∵60°角终边上一点P的坐标为(1，m)，∴tan60°＝，∵tan60°＝，∴m＝.答案：9．若α＝1560°，角θ与α终边相同，且－360°＜θ＜360°，则θ＝________.解析：因为α＝1560°＝4×360°＋120°，所以与α终边相同的角为360°×k＋120°，k∈Z，令k＝－1或k＝0，可得θ＝－240°或θ＝120°.答案：120°或－240°10．在直角坐标系xOy中，O为坐标原点，A(，1)，将点A绕O逆时针旋转90°到B点，则B点坐标为__________．解析：依题意知OA＝OB＝2，∠AOx＝30°，∠BOx＝120°， 设点B坐标为(x，y)，则x＝2cos120°＝－1，y＝2sin120°＝，即B(－1，)．答案：(－1，)11．已知＝－，且lg(cosα)有意义．(1)试判断角α所在的象限；(2)若角α的终边上一点M，且|OM|＝1(O为坐标原点)，求m的值及sinα的值．解：(1)由＝－，得sinα<0，由lg(cosα)有意义，可知cosα>0，所以α是第四象限角．(2)因为|OM|＝1，所以2＋m2＝1，解得m＝±.又因为α是第四象限角，所以m<0，从而m＝－，sinα＝＝＝＝－.12．已知α为第三象限角．(1)求角终边所在的象限；(2)试判断tansincos的符号．解：(1)由2kπ＋π＜α＜2kπ＋，k∈Z，得kπ＋＜＜kπ＋，k∈Z， 当k为偶数时，角终边在第二象限；当k为奇数时，角终边在第四象限．故角终边在第二或第四象限．(2)当角在第二象限时，tan＜0，sin＞0,cos＜0，所以tansincos取正号；当角在第四象限时，tan＜0，sin＜0,cos＞0，所以tansincos也取正号．因此tansincos取正号．B级1．若－<α<－，从单位圆中的三角函数线观察sinα，cosα，tanα的大小是(　　)A．sinαOM>MP，故有sinα0可知角α为第一或第三象限角，画出单位圆如图．又sinα>cosα，用正弦线、余弦线得满足条件的角α的终边在如图所示的阴影部分(不包括边界)，即角α的取值范围是∪.　3．已知角θ的终边过点P(－4a,3a)(a≠0)．(1)求sinθ＋cosθ的值；(2)试判断cos(sinθ)·sin(cosθ)的符号．解：(1)因为角θ的终边过点P(－4a,3a)(a≠0)，所以x＝－4a，y＝3a，r＝5|a|，当a＞0时，r＝5a，sinθ＋cosθ＝－＝－；当a＜0时，r＝－5a，sinθ＋cosθ＝－＋＝.(2)当a＞0时，sinθ＝∈，cosθ＝－∈，则cos(sinθ)·sin(cosθ)＝cos·sin＜0；当a＜0时，sinθ＝－∈，cosθ＝∈，则cos(sinθ)·sin(cosθ)＝cos·sin＞0. 综上，当a＞0时，cos(sinθ)·sin(cosθ)的符号为负；当a＜0时，cos(sinθ)·sin(cosθ)的符号为正． 第二节