高考数学考点归纳之绝对值不等式 12页

60.01 KB
2022-03-30 发布

高考数学考点归纳之绝对值不等式

关闭预览

12页
当前文档由用户上传发布，收益归属用户

1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
网站客服QQ：403074932

高考数学考点归纳之绝对值不等式一、基础知识1．绝对值三角不等式定理1：如果a，b是实数，则|a＋b|≤|a|＋|b|，当且仅当ab≥0时，等号成立．定理2：如果a，b，c是实数，那么|a－c|≤|a－b|＋|b－c|，当且仅当(a－b)(b－c)≥0时，等号成立．　　　↓|a|－|b|≤|a－b|≤|a|＋|b|，当且仅当|a|≥|b|且ab≥0时，左边等号成立，当且仅当ab≤0时，右边等号成立.2．绝对值不等式的解法　(1)|x|a型不等式的解法不等式a>0a＝0a<0|x|a{x|x>a或x<－a}{x|x∈R且x≠0}R(2)|ax＋b|≤c(c＞0)和|ax＋b|≥c(c>0)型不等式的解法：①|ax＋b|≤c⇔－c≤ax＋b≤c；②|ax＋b|≥c⇔ax＋b≥c或ax＋b≤－c.|x－a|＋|x－b|≥c和|x－a|＋|x－b|≤c型不等式的解法及体现数学思想①利用绝对值不等式的几何意义求解，体现了数形结合的思想；②利用“零点分段法”求解，体现了分类讨论的思想；③通过构造函数，利用函数的图象求解，体现了函数与方程的思想. 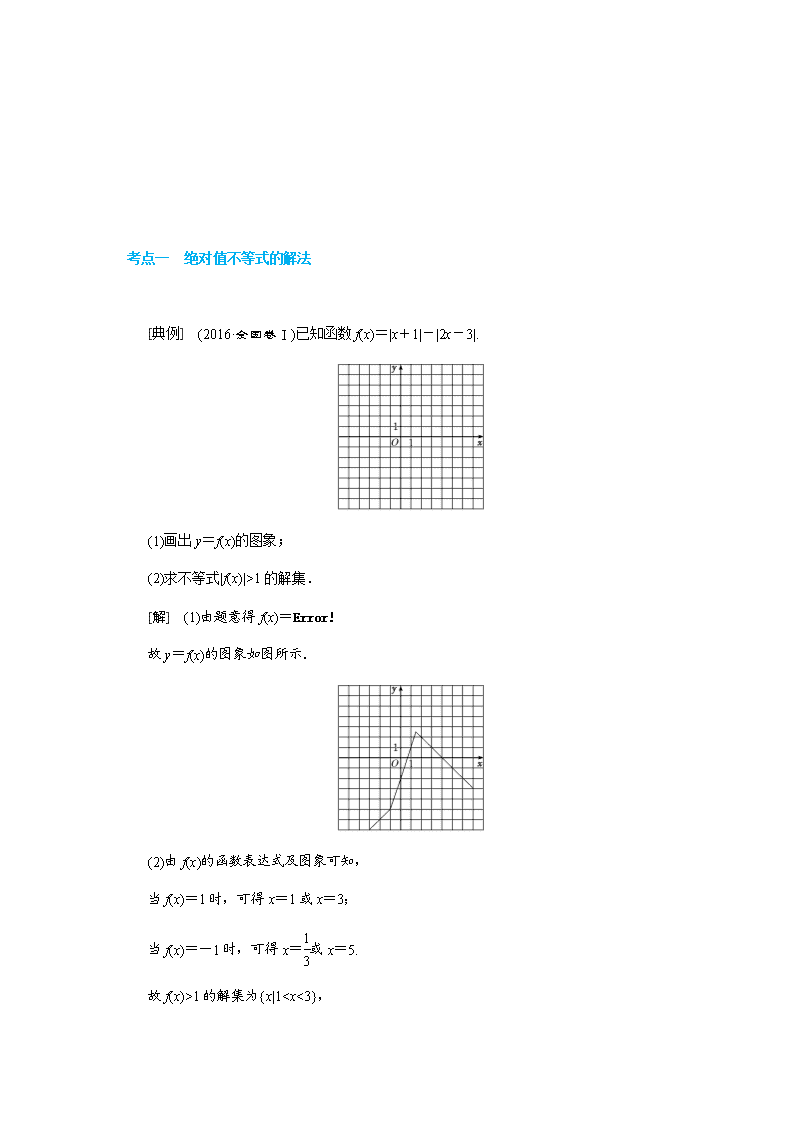[典例]　(2016·全国卷Ⅰ)已知函数f(x)＝|x＋1|－|2x－3|.(1)画出y＝f(x)的图象；(2)求不等式|f(x)|>1的解集．[解]　(1)由题意得f(x)＝故y＝f(x)的图象如图所示．(2)由f(x)的函数表达式及图象可知，当f(x)＝1时，可得x＝1或x＝3；当f(x)＝－1时，可得x＝或x＝5.故f(x)>1的解集为{x|11的解集为.[题组训练]1．解不等式|x＋1|＋|x－1|≤2.解：当x<－1时，原不等式可化为－x－1＋1－x≤2，解得x≥－1，又因为x<－1，故无解；当－1≤x≤1时，原不等式可化为x＋1＋1－x＝2≤2，恒成立；当x>1时，原不等式可化为x＋1＋x－1≤2，解得x≤1，又因为x>1，故无解；综上，不等式|x＋1|＋|x－1|≤2的解集为[－1,1]．2．(2019·沈阳质检)已知函数f(x)＝|x－a|＋3x，其中a∈R.(1)当a＝1时，求不等式f(x)≥3x＋|2x＋1|的解集；(2)若不等式f(x)≤0的解集为{x|x≤－1}，求a的值．解：(1)当a＝1时，f(x)＝|x－1|＋3x.法一：由f(x)≥3x＋|2x＋1|，得|x－1|－|2x＋1|≥0，当x>1时，x－1－(2x＋1)≥0，得x≤－2，无解；当－≤x≤1时，1－x－(2x＋1)≥0，得－≤x≤0；当x<－时，1－x－(－2x－1)≥0，得－2≤x<－.∴不等式的解集为{x|－2≤x≤0}．法二：由f(x)≥3x＋|2x＋1|，得|x－1|≥|2x＋1|，两边平方，化简整理得x2＋2x≤0，解得－2≤x≤0，∴不等式的解集为{x|－2≤x≤0}．(2)由|x－a|＋3x≤0，可得或即或当a>0时，不等式的解集为.由－＝－1，得a＝2.当a＝0时，不等式的解集为{x|x≤0}，不合题意．当a<0时，不等式的解集为.由＝－1，得a＝－4.综上，a＝2或a＝－4.[典例]　(2019·湖北五校联考)已知函数f(x)＝|2x－1|，x∈R.(1)解不等式f(x)<|x|＋1；(2)若对x，y∈R，有|x－y－1|≤，|2y＋1|≤，求证：f(x)<1.[解]　(1)∵f(x)<|x|＋1，∴|2x－1|<|x|＋1，即或或得≤x<2或0(|2x－1|＋|2x＋1|)min即可．由于|2x－1|＋|2x＋1|＝|1－2x|＋|2x＋1|≥|1－2x＋(2x＋1)|＝2，当且仅当(1－2x)(2x＋1)≥0，即x∈时等号成立，故m>2.所以m的取值范围是(2，＋∞)．[解题技法]　两招解不等式问题中的含参问题(1)转化①把存在性问题转化为求最值问题；②不等式的解集为R是指不等式的恒成立问题；③不等式的解集为∅的对立面也是不等式的恒成立问题，此类问题都可转化为最值问题，即f(x)＜a恒成立⇔a＞f(x)max，f(x)＞a恒成立⇔a＜f(x)min.(2)求最值求含绝对值的函数最值时，常用的方法有三种：①利用绝对值的几何意义；②利用绝对值三角不等式，即|a|＋|b|≥|a±b|≥||a|－|b||；③利用零点分区间法．[题组训练]1．(2018·全国卷Ⅱ)设函数f(x)＝5－|x＋a|－|x－2|.(1)当a＝1时，求不等式f(x)≥0的解集；(2)若f(x)≤1，求a的取值范围．解：(1)当a＝1时，f(x)＝当x<－1时，由2x＋4≥0，解得－2≤x<－1，当－1≤x≤2时，显然满足题意，当x>2时，由－2x＋6≥0，解得24时，由2x－6≤5，得41的解集；(2)若x∈(0,1)时不等式f(x)>x成立，求a的取值范围．解：(1)当a＝1时，f(x)＝|x＋1|－|x－1|，即f(x)＝故不等式f(x)>1的解集为.(2)当x∈(0,1)时|x＋1|－|ax－1|>x成立等价于当x∈(0,1)时|ax－1|<1成立．若a≤0，则当x∈(0,1)时，|ax－1|≥1；若a>0，则|ax－1|<1的解集为，所以≥1，故0－x；(2)若关于x的不等式f(x)≤a2－2a的解集为R，求实数a的取值范围．解：(1)原不等式等价于f(x)＋x＞0，不等式f(x)＋x>0可化为|x－2|＋x>|x＋1|，当x<－1时，－(x－2)＋x>－(x＋1)，解得x>－3，即－3x＋1，解得x<1，即－1≤x<1；当x>2时，x－2＋x>x＋1，解得x>3，即x>3，综上所述，不等式f(x)＋x>0的解集为{x|－33}．(2)由不等式f(x)≤a2－2a可得|x－2|－|x＋1|≤a2－2a，∵|x－2|－|x＋1|≤|x－2－x－1|＝3，当且仅当x∈(－∞，－1]时等号成立，∴a2－2a≥3，即a2－2a－3≥0，解得a≤－1或a≥3. ∴实数a的取值范围为(－∞，－1]∪[3，＋∞)．6．已知函数f(x)＝|x－a|＋|x＋1|.(1)若a＝2，求不等式f(x)＞x＋2的解集；(2)如果关于x的不等式f(x)＜2的解集不是空集，求实数a的取值范围．解：(1)当a＝2时，f(x)＝不等式f(x)＞x＋2等价于或或，解得x＜1或x＞3，故原不等式的解集为{x|x＜1或x＞3}．(2)∵f(x)＝|x－a|＋|x＋1|≥|(x－a)－(x＋1)|＝|a＋1|，当(x－a)(x＋1)≤0时取等号．∴若关于x的不等式f(x)＜2的解集不是空集，只需|a＋1|＜2，解得－3＜a＜1，即实数a的取值范围是(－3,1)．7．已知函数f(x)＝|2x－a|＋a.(1)当a＝2时，求不等式f(x)≤6的解集；(2)设函数g(x)＝|2x－1|.当x∈R时，f(x)＋g(x)≥3，求a的取值范围．解：(1)当a＝2时，f(x)＝|2x－2|＋2.解不等式|2x－2|＋2≤6，得－1≤x≤3.因此f(x)≤6的解集为{x|－1≤x≤3}．(2)当x∈R时，f(x)＋g(x)＝|2x－a|＋a＋|1－2x|≥3，即＋≥.又min＝，所以≥，解得a≥2.所以a的取值范围是[2，＋∞)． 8．(2018·福州质检)设函数f(x)＝|x－1|，x∈R.(1)求不等式f(x)≤3－f(x－1)的解集；(2)已知关于x的不等式f(x)≤f(x＋1)－|x－a|的解集为M，若⊆M，求实数a的取值范围．解：(1)因为f(x)≤3－f(x－1)，所以|x－1|≤3－|x－2|⇔|x－1|＋|x－2|≤3⇔或或解得0≤x<1或1≤x≤2或2

高考数学考点归纳之绝对值不等式 12页