空间向量在立体几何中的应用重点知识高考真题模拟精选 16页

空间向量在立体几何中的应用 ‎【重要知识】‎ 一、 求平面法向量的方法与步骤：‎ 1、 选向量：求平面的法向量时，要选取两个相交的向量，如 2、 设坐标：设平面法向量的坐标为 3、 解方程：联立方程组，并解方程组 4、 定结论：求出的法向量中三个坐标不是具体的数值，而是比例关系。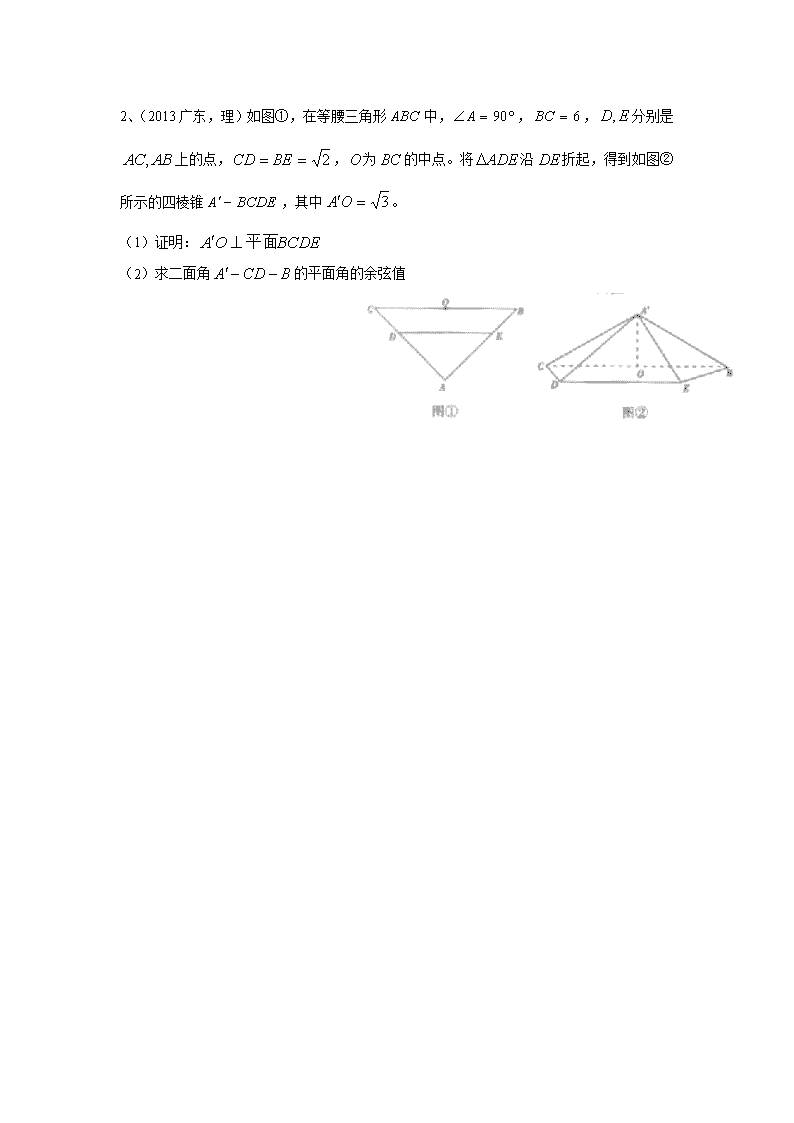设定某个坐标为常 ‎ 数得到其他坐标 二、 利用向量求空间角：‎ ‎1、求异面直线所成的角：‎ ‎ 设为异面直线，点为上任意两点，点为上任意两点，所成的角为，则 ‎【注】由于异面直线所成的角的范围是：，因此 2、 求直线与平面所成的角：‎ ‎ 设直线的方向向量为，平面的法向量为，直线与平面所成的角为，与所成的角为，则 ‎【注】由于直线与平面所成的角的范围是：，因此 3、 求二面角：‎ ‎ 设分别为平面的法向量，二面角为，则或，其中 三、 利用向量求空间距离：‎ 1、 求点到平面的距离 ‎ 设平面的法向量为，，则点到平面的距离为 1、 求两条异面直线的距离 ‎ 设是两条异面直线，是公垂线段的方向向量，分别为上的任意两点，则的距离为 ‎【重要题型】‎ ‎1、（2012广东，理）如图所示，在四棱锥中，底面为矩形，，点在线段上， ‎（1）证明： ‎（2）若，求二面角的正切值 ‎ ‎ ‎2、（2013广东，理）如图①，在等腰三角形中，，，分别是上的点，，为的中点。将沿折起，得到如图②所示的四棱锥，其中。‎ ‎（1）证明： ‎（2）求二面角的平面角的余弦值 ‎3、（2009广东，理）如图，已知正方体的棱长为2，点是正方形的中心，点分别是棱、的中点，设分别是点在平面内的正投影。‎ ‎（1）求以为顶点，以四边形在平面内的正投影为底面边界的棱锥的体积；‎ ‎（2）证明：直线；‎ ‎（3）求异面直线与所成角的正弦值。‎ ‎4、（2013课标，理）如图，直三棱柱中，分别是的中点， ‎（1）证明：；‎ ‎（2）求二面角的正弦值.‎ ‎5、（2012辽宁，理）如图，直三棱柱，，，点分别为和的中点 ‎（1）证明：；‎ ‎（2）若二面角为直二面角，求的值.‎ ‎6、（2010辽宁，理）已知三棱锥中，，，，为上一点，，分别为的中点。‎ ‎（1）证明：；‎ ‎（2）求与平面所成角的大小.‎ ‎ ‎ ‎7、（2010广东，理）如图，是半径为的半圆，为直径，点为的中点，点和点为线段的三等分点，平面外一点满足， ‎（1）证明：；‎ ‎（2）已知点分别为线段上的点，使得，，求平面与平面所成二面角的正弦值.‎ ‎8、（2013汕头高二统考，理）在四棱锥中，平面，是正三角形，与的交点恰好是中点，又，，点在线段上，且．‎ ‎（1）求证：；‎ ‎（2）求证：平面;‎ ‎（3）求二面角的余弦值．‎ ‎【参考答案】‎ ‎1、（1）证明：，， 又，， ， ‎（2）解：，， ‎ 是正方形 ‎ 建立如图所示的坐标系，则 ，，， ， ‎ ， 设平面的一个法向量为 则，即 令，则，即 设平面的一个法向量为，‎ 则，即 令，则，即 ‎ 设二面角的大小为，则， ‎ ‎2、（1）证明：连接 ‎ 由图①得， ‎ 在中，由余弦定理可得，‎ ‎ ，即 ‎ 由翻折的不变性可知， ‎ ， ‎ 同理可证， ‎ 又， ‎（2）解：以点为原点，建立空间直角坐标系如图所示 ‎ 则 ‎ 所以， ‎ 设平面的一个法向量为，则 ‎ 即 ‎ 令，则，即 由（1）知，为平面的一个法向量 即求二面角的平面角的余弦值为 ‎3、（1）解：依题意得，，且四边形在平面内的正投影为四边形 ‎ 点是正方形的中心， ‎ ‎ 故所求的四棱锥的体积为 ‎（2）证明：由（1）知，与都是等腰直角三角形 ‎ ，即 ‎ 又，， ‎ ， ‎（3）解：以为原点，分别为轴，轴，轴的正向，为1个单位长度，建立空间直角坐标系，则 ， ‎4、（1）证明：连接交于点，则为中点 ‎ 又是中点，连接，则 ‎ ，， ‎（2）由得， 以为坐标原点，的方向为轴正方向，建立如图所示的空间直角坐标系，设，则 ，，， ‎ ，， 设是平面的法向量，则 ，即，可取 同理，设是平面的法向量，则 ，即，可取 从而，故 即二面角的正弦值为 ‎5、（1）证明：连接 ‎ 三棱柱为直三棱柱，为的中点 ‎ 为的中点 ‎ 又为的中点 ‎ ‎ ， ‎ ‎（2）以为坐标原点，分别以直线为轴，轴，轴的正方向建立空间直角坐标系，如图所示：‎ 设，则 于是，， ，， 因此，， 设是平面的法向量，‎ 由得，，可取 同理，设是平面的法向量，‎ 由得，，可取 为直二面角 ，即，解得 ‎6、（1）证明：设，以为原点，分别为轴正方向建立空间直角坐标系，如图所示：‎ 则 由可知， ‎（2） 设为平面的一个法向量 由得，，可取 设与平面所成角为，则 ‎7、（1）证明：为 的中点，，为直径 ‎ ‎ ‎ ‎ 又， ‎ ， ‎（2）如图，以为原点，分别为轴正方向，过作平面的垂线，建立空间直角坐标系，连接 由此得，‎ 设平面的法向量为，‎ 由得， ，可取 同理，设平面的法向量为，可取 平面与平面所成二面角的正弦值为 ‎8、证明：（1） 因为是正三角形，是中点，‎ 所以,即………………1分 又因为，平面，………………2分 又，所以平面………………3分 又平面，所以………………4分 ‎（2）在正三角形中，………………5分 在中，因为为中点，，所以 ‎，所以，所以………………6分 在等腰直角三角形中，，，‎ 所以，，所以………………8分 又平面，平面，所以平面………………9分 ‎（3）因为，‎ 所以，分别以为轴, 轴, 轴建立如图的空间直角坐标系，‎ 所以………………10分 由（2）可知，为平面的法向量………………11分 ‎，‎ 设平面的一个法向量为,‎ 则，即，‎ 令则平面的一个法向量为………………12分 设二面角的大小为(显然为锐角)， ‎ ‎ 则 所以二面角余弦值为………………14分