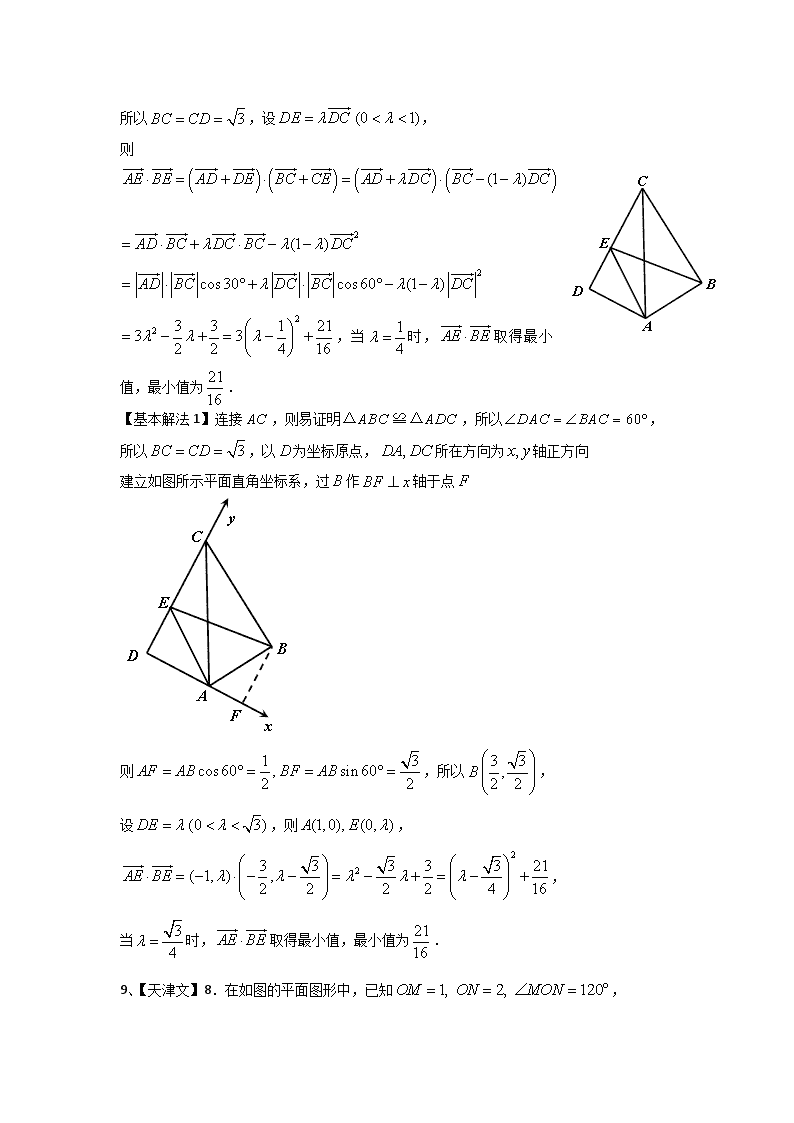- 553.00 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2018高考分类汇编 ——平面向量
1、【北京理】6.设,均为单位向量,则“”是“”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:C;
解析:等号两边分别平方得与等价,故选C.
考点:考查平面向量的数量积性质及充分必要条件的判定;
备注:高频考点.
2、【北京文】9.设向量,若,则 ______.
答案:
【解析】因为
所以
由 得,
所以,解得
【考点】本题考查向量的坐标运算,考查向量的垂直。
3、【1卷文7理6】6.在中,为边上的中线,为的中点,则
A. B. C. D.
答案:A
解析:在中,为边上的中线,为的中点,,故选A.
4、【2卷理】4.已知向量,满足,,则
A.4 B.3 C.2 D.0
【答案】B
【解析】,故选B.
5、【2卷文】4.已知向量,满足,,则
A.4 B.3 C.2 D.0
【答案】B
解析:向量满足,则,故选B.
6、【3卷文理】13.已知向量,,,若,则 .
解析:依题意可得,又,
所以,解得.
点评:本题主要考查向量的坐标运算,以及两向量共线的坐标关系,属于基础题.
7、【上海】8.在平面直角坐标系中,已知点、,、是轴上的两个动点,且,则的最小值为 .
答案:
解析:设,则,
,最小值为.
解法2:
取中点,则.显然(当关于原点对称).
所以.则.
8、【天津理】8.如图,在平面四边形中,,,,,若点为边上的动点,则的最小值为( )
A. B. C. D.3
【答案】A
【基本解法1】连接,则易证明,所以
所以,设,
则
,当时,取得最小值,最小值为.
【基本解法1】连接,则易证明,所以,
所以,以为坐标原点,所在方向为轴正方向
建立如图所示平面直角坐标系,过作轴于点
则,所以,
设,则,
,
当时,取得最小值,最小值为.
9、【天津文】8.在如图的平面图形中,已知,
,则的值为( )
A. B. C. D.0
【答案】C
解析:,
则.
10、【浙江卷】9.已知是平面向量, 是单位向量,若非零向量与的夹角为,向量满足,则的最小值是( )
A. B. C.2 D.
【答案】A
解析:解法1:(配方法)由得,即,因此.如图,,,,则向量的终点在以为圆心,1为半径的圆上,而的终点在射线上,,问题转化为圆上的点与射线上的点连线长度最小,显然其最小值为圆心到射线的距离减去半径即为.
解法2:(向量的直径圆式)由,得,所以,
如图,,则,即终点在以为直径的圆上,以下同解法1.
解法3:(绝对值性质的应用)由,得,即,
因此,而由图形得,
所以,所以的最小值为.
解法4:(坐标法)设起点均为原点,设,,则的终点在射线上,由,得,即,所以向量的终点在圆
上,的最小值即为求圆上一点到射线上一点的最小距离,
即为.