山东高考文科数学立体几何大题及答案汇编 7页

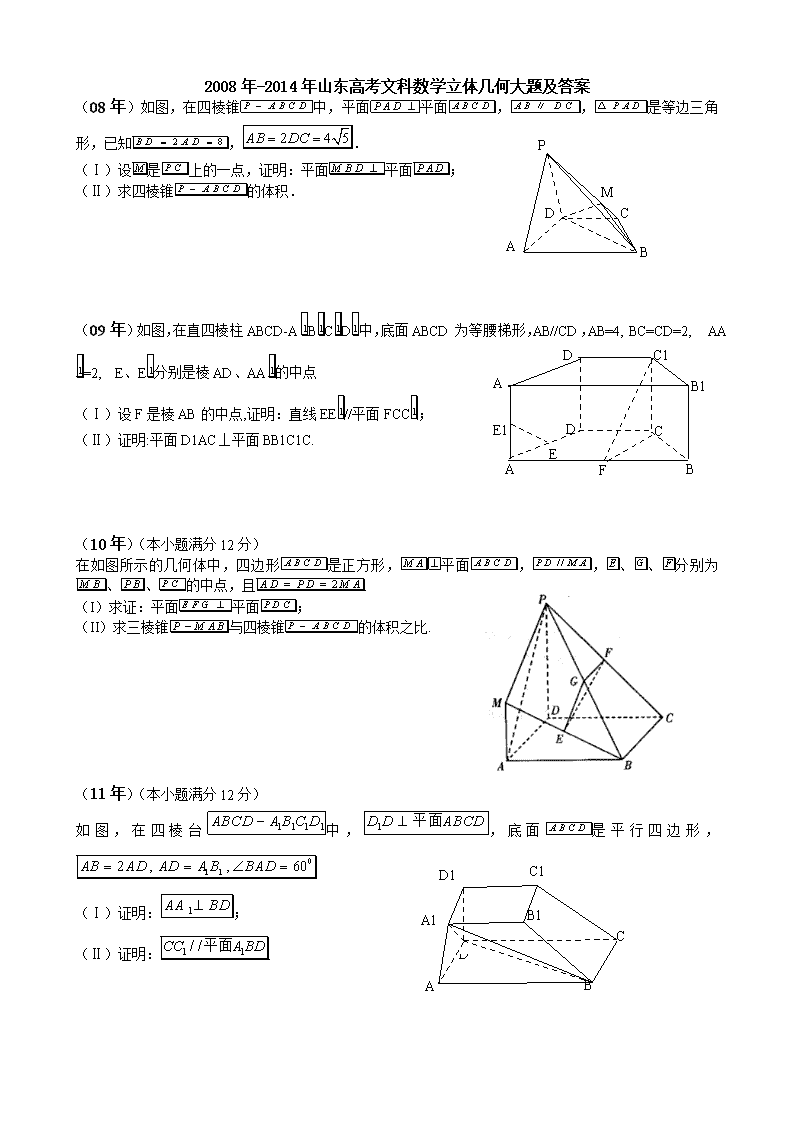
‎2008年-2014年山东高考文科数学立体几何大题及答案 ‎（08年）A B C M P D 如图，在四棱锥中，平面平面，，是等边三角形，已知，．‎ ‎（Ⅰ）设是上的一点，证明：平面平面；‎ ‎（Ⅱ）求四棱锥的体积．‎ ‎（09年）E ‎ A ‎ B ‎ C ‎ F ‎ E1 ‎ A1 ‎ B1 ‎ C1 ‎ D1 ‎ D ‎ 如图，在直四棱柱ABCD-ABCD中，底面ABCD为等腰梯形，AB//CD，AB=4, BC=CD=2, AA=2, E、E分别是棱AD、AA的中点 ‎（Ⅰ）设F是棱AB的中点,证明：直线EE//平面FCC；‎ ‎（Ⅱ）证明:平面D1AC⊥平面BB1C1C.‎ ‎（10年）（本小题满分12分）‎ 在如图所示的几何体中，四边形是正方形，平面，，、、分别为、、的中点，且.‎ ‎（I）求证：平面平面；‎ ‎（II）求三棱锥与四棱锥的体积之比.‎ ‎（11年）（本小题满分12分）‎ D B1‎ D1‎ C1‎ C B A A1‎ 如图，在四棱台中，，底面是平行四边形，‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）证明：.‎ ‎（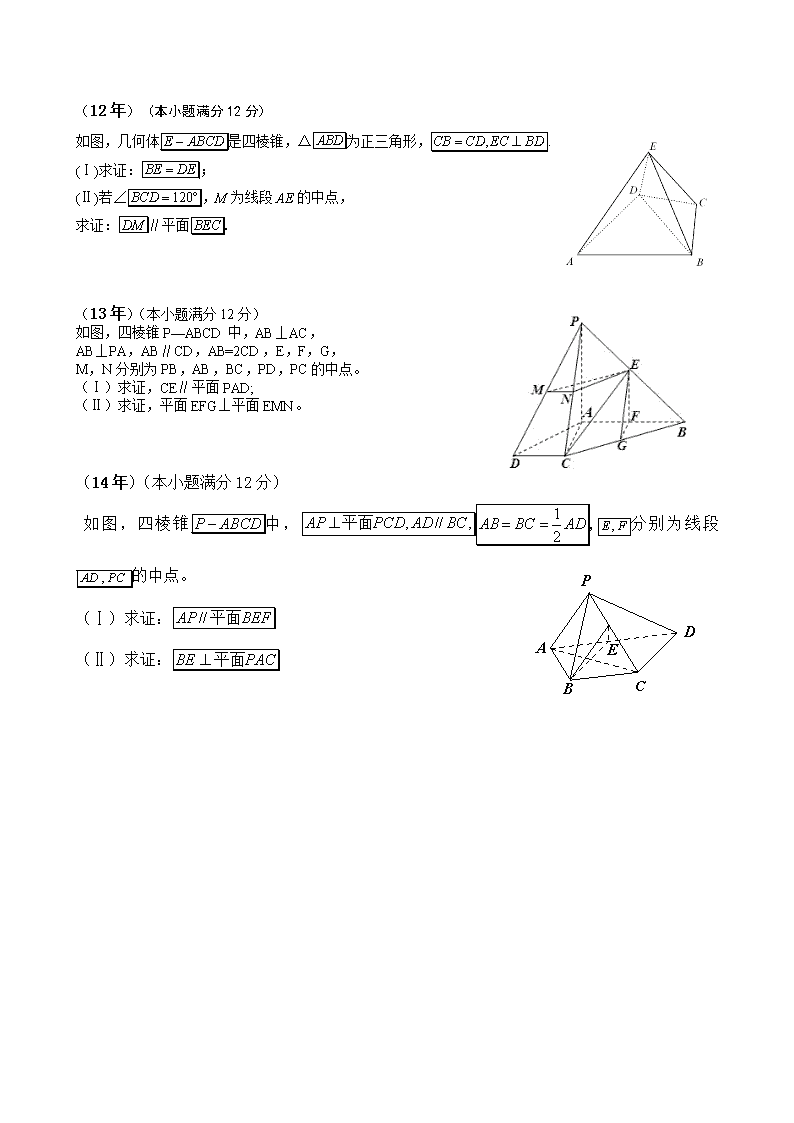12年） (本小题满分12分)‎ 如图，几何体是四棱锥，△为正三角形，.‎ ‎(Ⅰ)求证：；‎ ‎(Ⅱ)若∠，M为线段AE的中点，‎ 求证：∥平面.‎ ‎（13年）（本小题满分12分）‎ 如图，四棱锥P—ABCD中，AB⊥AC，‎ AB⊥PA，AB∥CD，AB=2CD，E，F，G，‎ M，N分别为PB，AB，BC，PD，PC的中点。‎ ‎（Ⅰ）求证，CE∥平面PAD;‎ ‎（Ⅱ）求证，平面EFG⊥平面EMN。‎ ‎（14年）（本小题满分12分）‎ ‎ 如图，四棱锥中，,分别为线段的中点。‎ ‎（Ⅰ）求证：‎ ‎（Ⅱ）求证：‎ ‎ ‎ 答案 ‎08年 解：（Ⅰ）证明：在中，‎ 由于，，，‎ A B C M P D O 所以．‎ 故．‎ 又平面平面，平面平面，‎ 平面，‎ 所以平面，‎ 又平面，‎ 故平面平面．‎ ‎（Ⅱ）解：过作交于，‎ 由于平面平面，‎ 所以平面．‎ 因此为四棱锥的高，‎ 又是边长为4的等边三角形．‎ 因此．‎ 在底面四边形中，，，‎ 所以四边形是梯形，在中，斜边边上的高为，‎ 此即为梯形的高，‎ 所以四边形的面积为．‎ 故．‎ ‎09年 解：（Ⅰ）证明：‎ 在直四棱柱ABCD-ABCD中，取A1B1的中点F1，‎ E ‎ A ‎ B ‎ C ‎ F ‎ E1 ‎ A1 ‎ B1 ‎ C1 ‎ D1 ‎ D ‎ F1‎ 连接A1D，C‎1F1，CF1，因为AB=4, CD=2,且AB//CD，‎ 所以CDA1F1，A1F1CD为平行四边形，所以CF1//A1D，‎ 又因为E、E分别是棱AD、AA的中点，所以EE1//A1D，‎ 所以CF1//EE1，又因为平面FCC，平面FCC，‎ 所以直线EE//平面FCC.‎ E ‎ A ‎ B ‎ C ‎ F ‎ E1 ‎ A1 ‎ B1 ‎ C1 ‎ D1 ‎ D ‎ ‎（Ⅱ）连接AC,在直棱柱中，CC1⊥平面ABCD,AC平面ABCD,‎ 所以CC1⊥AC,因为底面ABCD为等腰梯形，AB=4, BC=2,‎ ‎ F是棱AB的中点,所以CF=CB=BF，△BCF为正三角形，‎ ‎,△ACF为等腰三角形，且 所以AC⊥BC, 又因为BC与CC1都在平面BB1C1C内且交于点C,‎ 所以AC⊥平面BB1C1C,而平面D1AC,‎ 所以平面D1AC⊥平面BB1C1C.‎ ‎10年 解：（I）证明：由已知 ‎ 所以 ‎ ‎ 又 ，‎ ‎ 所以 ‎ ‎ 因为 四边形为正方形，‎ ‎ 所以 ,‎ ‎ 又 ，‎ ‎ 因此 ‎ ‎ 在中，因为分别为的中点，‎ ‎ 所以 ‎ ‎ 因此 ‎ ‎ 又 ，‎ ‎ 所以 ．‎ ‎ （Ⅱ）解：因为,四边形为正方形，不妨设，‎ ‎ 则 ，‎ ‎ 所以·‎ ‎ 由于的距离，且 ‎ 所以即为点到平面的距离，‎ ‎ 三棱锥 ‎ ‎ 所以 ‎ ‎11年 解：（I）证法一：‎ 因为平面ABCD，且平面ABCD， 所以，‎ 又因为AB=2AD，， 在中，由余弦定理得 ‎，‎ 所以， 因此， 又所以 又平面ADD1A1， 故 证法二：‎ 因为平面ABCD，且平面ABCD，‎ 所以 取AB的中点G，连接DG，‎ 在中，由AB=2AD得AG=AD，‎ 又，所以为等边三角形。‎ 因此GD=GB， 故， 又 所以平面ADD1A1， 又平面ADD1A1， 故 ‎ （II）连接AC，A‎1C1，‎ 设，连接EA1 因为四边形ABCD为平行四边形，‎ 所以 由棱台定义及AB=2AD=2A1B1知 A‎1C1//EC且A1C1=EC， 所以边四形A1ECC1为平行四边形，‎ 因此CC1//EA1， 又因为EA平面A1BD，平面A1BD， 所以CC1//平面A1BD。‎ ‎ ‎ ‎12年 解： (I)设中点为O，连接OC，OE，则由知，，‎ 又已知，所以平面OCE.‎ 所以，即OE是BD的垂直平分线， 所以.‎ ‎(II)取AB中点N，连接， ∵M是AE的中点，∴∥，‎ ‎∵△是等边三角形，∴.‎ 由∠BCD＝120°知，∠CBD＝30°，所以∠ABC＝60°+30°＝90°，即，‎ 所以ND∥BC， 所以平面MND∥平面BEC，故DM∥平面BEC.‎ ‎13年 解：(1)证法一：取PA的中点H，连接EH，DH.，‎ 因为E为PB的中点，所以EH∥AB，EH＝.‎ 又AB∥CD，CD＝，所以EH∥CD，EH＝CD.因此四边形DCEH是平行四边形，所以CE∥DH.‎ 又DH平面PAD，CE平面PAD，因此CE∥平面PAD.‎ 证法二：连接CF.‎ 因为F为AB的中点，所以AF＝.‎ 又CD＝，所以AF＝CD.又AF∥CD，‎ 所以四边形AFCD为平行四边形．因此CF∥AD.‎ 又CF平面PAD，所以CF∥平面PAD.‎ 因为E，F分别为PB，AB的中点，所以EF∥PA.‎ 又EF平面PAD，所以EF∥平面PAD.‎ 因为CF∩EF＝F，故平面CEF∥平面PAD.‎ 又CE平面CEF，所以CE∥平面PAD.‎ ‎(2)证明：因为E，F分别为PB，AB的中点，‎ 所以EF∥PA. 又AB⊥PA，所以AB⊥EF. 同理可证AB⊥FG.‎ 又EF∩FG＝F，EF平面EFG，FG平面EFG， 因此AB⊥平面EFG.‎ 又M，N分别为PD，PC的中点， 所以MN∥CD. 又AB∥CD，所以MN∥AB.‎ 因此MN⊥平面EFG. 又MN平面EMN， 所以平面EFG⊥平面EMN.‎ ‎14年 解：（Ⅰ）连接AC交BE于点O，连接OF，不妨设AB=BC=1,则AD=2‎ 四边形ABCE为菱形 ‎ 又 ‎（Ⅱ）‎ ‎,‎ ‎,‎