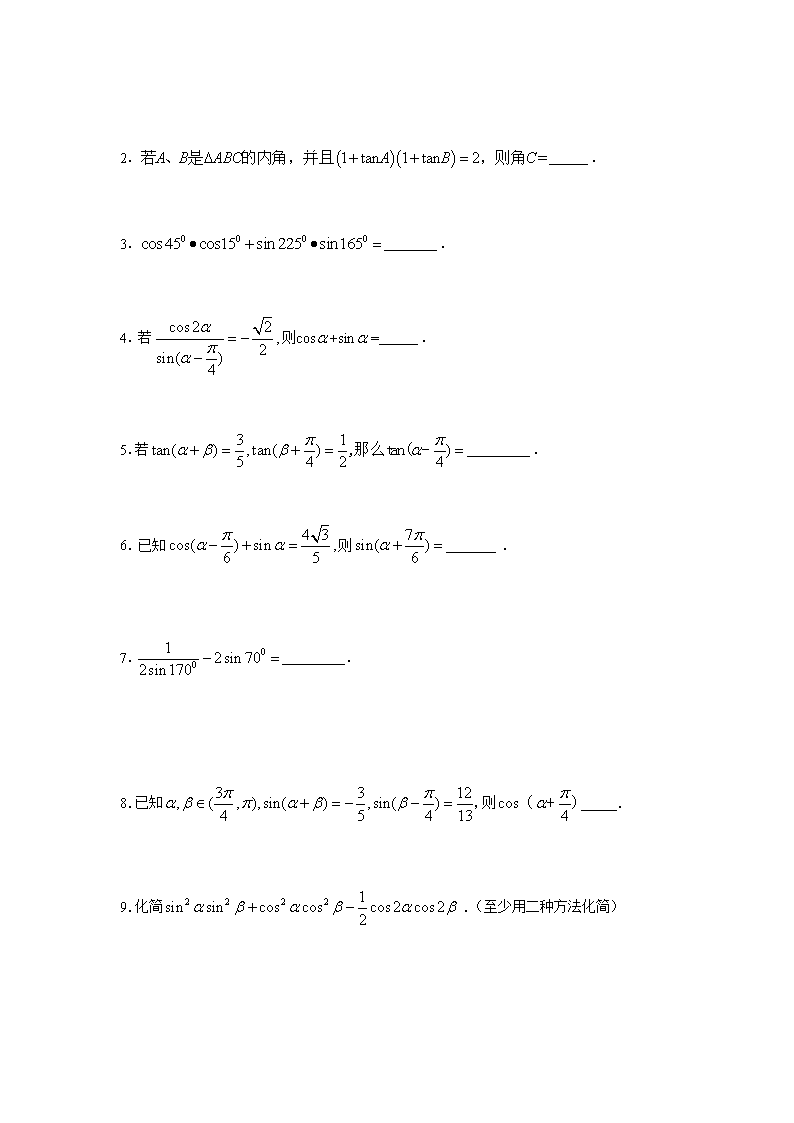高考文科数学第一轮复习学案2 6页

‎2013届高三数学（文）复习学案：三角函数的化简、求值与证明（二）‎ 一、课前准备：‎ ‎【自主梳理】‎ ‎ 此类题型考查三角函数的变换.解此类题应根据考题的特点灵活地正用、逆用，变形运用和、差、倍角公式和诱导公式，进行化简、求值 证明.‎ ‎ 【自我检测】‎ ‎1．= ．‎ ‎2．= ．‎ ‎3． ．‎ ‎4． ．‎ ‎5． ．‎ 二、课堂活动：‎ ‎【例1】填空题：‎ ‎ ．‎ ‎（2） ．‎ ‎（3）= ．‎ ‎（4） ．‎ ‎【例2】① ‎ ‎② ‎ ‎【例3】已知函数．（Ⅰ）求函数的最小正周期和值域；（Ⅱ）若为第二象限角，且，求的值．‎ 课堂小结 三、课后作业 ‎1 ‎ ‎2 ‎ ‎3 ‎ ‎4 若则cos+sin= ‎ ‎5若 ‎ ‎6 已知则 ‎ ‎7 ‎ ‎8已知则 ‎ ‎9化简 （至少用二种方法化简）‎ ‎10如图，在平面直角坐标系中，锐角和钝角的终边分别与单位圆交于，两点．‎ ‎⑴如果、两点的纵坐标分别为、，求和；‎ ‎⑵在⑴的条件下，求的值；‎ ‎⑶已知点，求函数的值域． ‎ 四、 纠错分析 错题卡 题 号 错 题 原 因 分 析 参考答案：‎ ‎【自我检测】 3. 1 4. 5. ‎ ‎【例题】例1：（1）20 （2） （3） （4）‎ 例2：证明：‎ ‎②‎ ‎②：‎ 例3【解】（Ⅰ）因为 ， ‎ 所以函数的周期为，值域为． ‎ ‎（Ⅱ）因为 ，所以 ，即 ‎ 因为 ‎ ‎， ‎ 又因为为第二象限角， 所以 ． ‎ 所以 ‎【课后作业】： 3. 4、 5、 6、 7、1 8、‎ ‎9、解：法1：从角出发，异角化同角 原式==‎ 法2：从名出发，异名化同名 原式= ‎ ‎=‎ 法3：从“幂”入手，高次化低次 ‎ ‎ 原式=‎ 法4：从形入手，利用配方法对二次项配方。‎ 原式=‎ ‎10、【解】（1）根据三角函数的定义，得，．‎ 又是锐角，所以 ‎ ‎（2）由（1）知．因为是钝角，所以．‎ 所以． ‎ ‎（3）由题意可知，，．‎ 所以，‎ 因为，所以，‎ 从而，因此函数的值域为． ‎