高考数学复习讲练21曲线方程圆的方程 6页

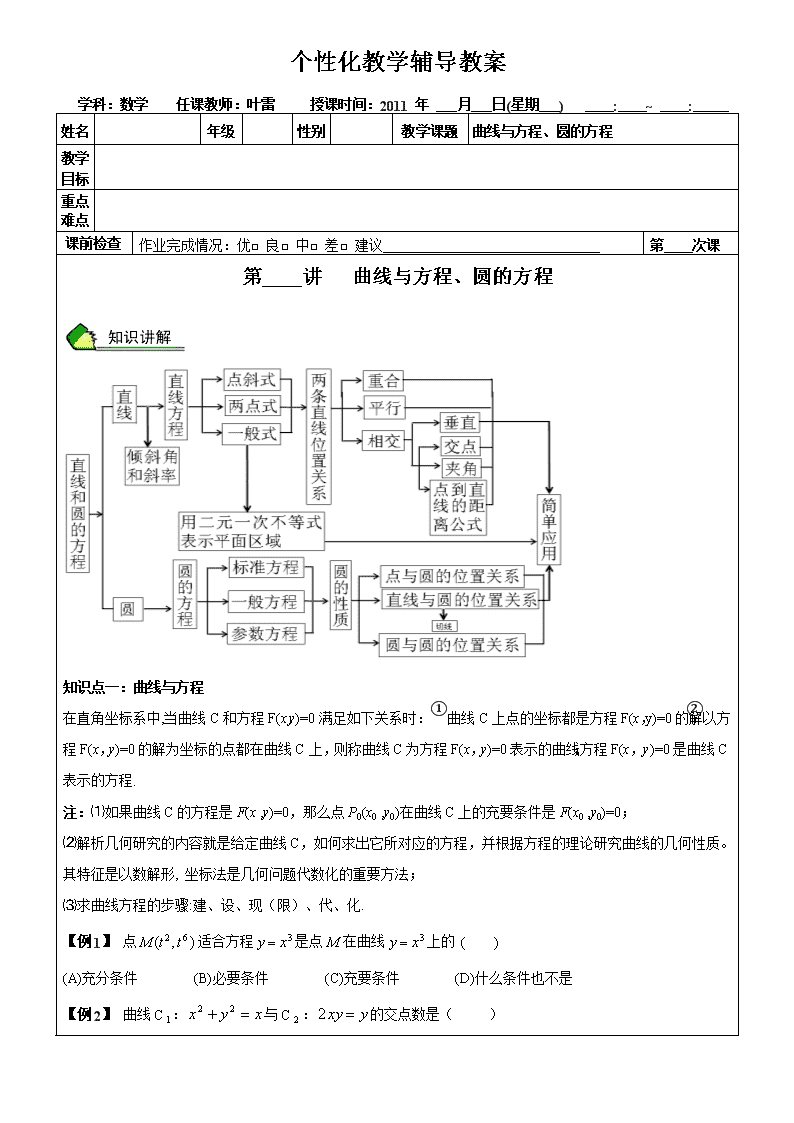
个性化教学辅导教案 学科：数学 任课教师：叶雷 授课时间：2011 年 月 日(星期 ) : ~ : ‎ 姓名 年级 性别 ‎ ‎ 教学课题 ‎ 曲线与方程、圆的方程 教学 目标 重点 难点 课前检查 作业完成情况：优□ 良□ 中□ 差□ 建议_______________________________‎ 第 次课 第 讲 曲线与方程、圆的方程 知识点一：曲线与方程 在直角坐标系中,当曲线C和方程F(x，y)=0满足如下关系时：①曲线C上点的坐标都是方程F(x，y)=0的解；②以方程F(x，y)=0的解为坐标的点都在曲线C上，则称曲线C为方程F(x，y)=0表示的曲线；方程F(x，y)=0是曲线C表示的方程.‎ 注：⑴如果曲线C的方程是F(x ,y)=0，那么点P0(x0 ,y0)在曲线C上的充要条件是F(x0 ,y0)=0；‎ ‎⑵解析几何研究的内容就是给定曲线C，如何求出它所对应的方程，并根据方程的理论研究曲线的几何性质。其特征是以数解形, 坐标法是几何问题代数化的重要方法；‎ ‎⑶求曲线方程的步骤:建、设、现（限）、代、化.‎ ‎【例1】 点适合方程是点在曲线上的 ( )‎ ‎(A)充分条件 (B)必要条件 (C)充要条件 (D)什么条件也不是 ‎【例2】 曲线C：与C：的交点数是（ ）‎ ‎(A)1个 (B) 2个 (C)3个 (D)4个 ‎【例3】 已知定点，，点M与A、B两点所在直线的斜率之积等于，则点M的轨迹方程 是 。‎ ‎【例4】 已知圆和两点A（0，4），B（4，0）当点P在圆上运动时，求的重心的轨迹方程.‎ ‎【例5】 如图，圆与圆的半径都是1，. 过动点分别作圆、圆的切线（分别为切点），使得.试建立适当的坐标系，并求动点的轨迹方程.‎ ‎ ‎ 知识点二：圆的方程 确定圆的方程需要有三个互相独立的条件。的圆方程的适用范围。‎ 一、圆的方程形式:‎ ‎⑴圆的标准方程：(x-a)2+(y-b)2=r2,其中（a,b）是圆心坐标,r是圆的半径；‎ ‎⑵圆的一般方程：x2+y2+Dx+Ey+F=0（D2+E2-4F>0）,圆心坐标为（-，-），半径为r=.‎ ‎⑶圆的参数方程：(x-a)2+(y-b)2=r2（r>0）的参数方程为:（为参数,表示旋转角），参数式常用来表示圆周上的点。‎ 注：①确定圆的方程需要有三个互相独立的条件, 通常也用待定系数法;‎ ‎②圆的方程有三种形式，注意各种形式中各量的几何意义,使用时常数形结合充分运用圆的平面几何知识.‎ ‎③圆的直径式方程： ,其中是圆的一条直径的两个端点.（用向量可推导）.‎ 二、直线与圆的位置关系 直线与圆的位置关系有三种：相离、相切、相交，判定方法有两种：‎ ‎⑴代数法：直线：Ax+By+C=0，圆：x2+y2+Dx+Ey+F=0，联立得方程组 一元二次方程 ‎（2）几何法：直线:Ax+By+C=0，圆：(x-a)2+(y-b)2=r2，圆心（a，b）到直线的距离为d=，则 三、圆和圆的位置关系：‎ 设两圆圆心分别为O1、O2，半径分别为r1，r2，|O1O2|为圆心距，则两圆位置关系如下：‎ ‎①|O1O2|>r1+r2两圆外离；‎ ‎②|O1O2|=r1+r2两圆外切；‎ ‎③| r1-r2|<|O1O2|0，即7m2-6m-1<0，∴。‎ ‎⑵半径r=，‎ ‎ ∵ ,∴ 时，，∴ 0