北京高考文科数学试题及答案word版 4页

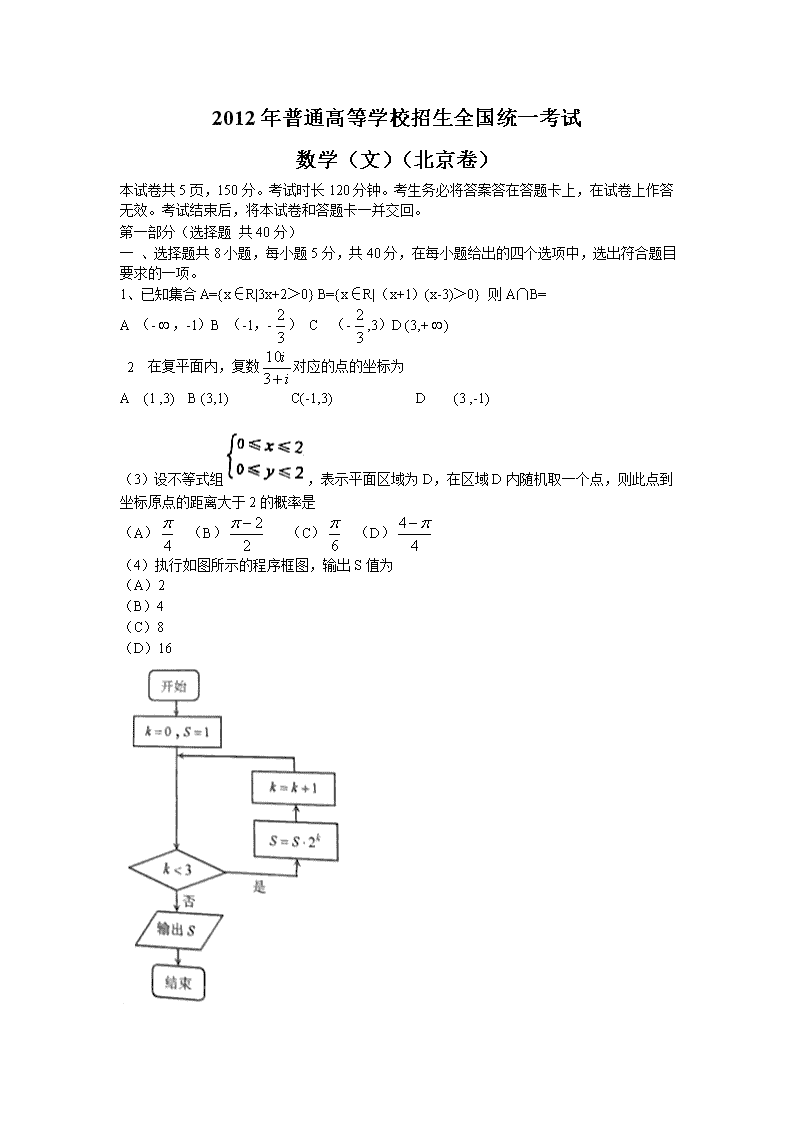
‎2012年普通高等学校招生全国统一考试 数学（文）（北京卷）‎ 本试卷共5页，150分。考试时长120分钟。考生务必将答案答在答题卡上，在试卷上作答无效。考试结束后，将本试卷和答题卡一并交回。‎ 第一部分（选择题 共40分）‎ 一 、选择题共8小题，每小题5分，共40分，在每小题给出的四个选项中，选出符合题目要求的一项。‎ ‎1、已知集合A={x∈R|3x+2＞0} B={x∈R|（x+1）(x-3)＞0} 则A∩B=‎ A （-，-1）B （-1，-） C （-,3）D (3,+)‎ ‎ 2 在复平面内，复数对应的点的坐标为 A (1 ,3) B (3,1) C(-1,3) D (3 ,-1)‎ ‎（3）设不等式组，表示平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是 ‎（A） （B） （C） （D）‎ ‎（4）执行如图所示的程序框图，输出S值为 ‎（A）2‎ ‎（B）4‎ ‎（C）8‎ ‎（D）16‎ ‎(5)函数f（x）＝的零点个数为 ‎（A）0 （B）1（C）2 （D）3‎ ‎（6）已知为等比数列，下面结论种正确的是 ‎（A）a1+a3≥‎2a2（B）（C）若a1=a3，则a1=a2（D）若a3＞a1，则a4＞a2‎ ‎（7）某三棱锥的三视图如图所示，该三棱锥的表面积是 ‎（A）28+（B）30+（C）56+（D）60+‎ ‎（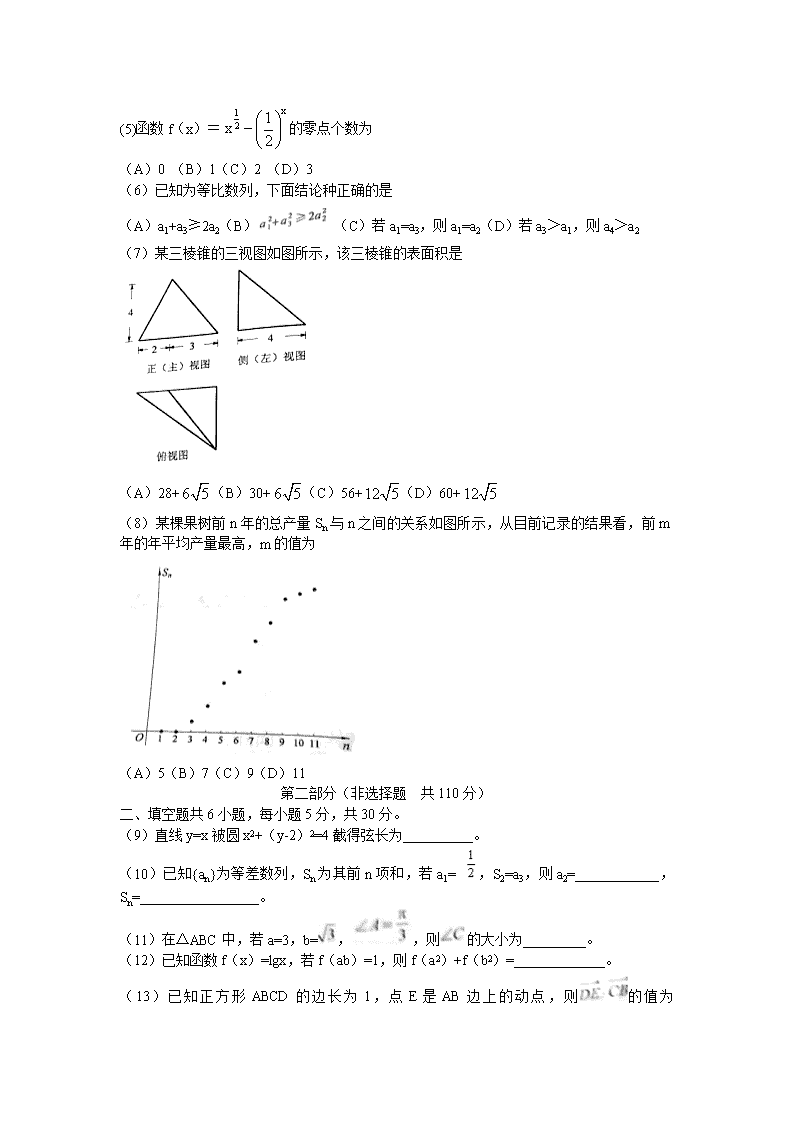8）某棵果树前n年的总产量Sn与n之间的关系如图所示，从目前记录的结果看，前m年的年平均产量最高，m的值为 ‎（A）5（B）7（C）9（D）11‎ ‎ 第二部分（非选择题 共110分）‎ 二、填空题共6小题，每小题5分，共30分。‎ ‎（9）直线y=x被圆x2+（y-2）2=4截得弦长为__________。‎ ‎（10）已知{an}为等差数列，Sn为其前n项和，若a1= ，S2=a3，则a2=____________，Sn=_________________。‎ ‎（11）在△ABC中，若a=3，b=，，则的大小为_________。‎ ‎（12）已知函数f（x）=lgx，若f（ab）=1，则f（a2）+f（b2）=_____________。‎ ‎（13）已知正方形ABCD的边长为1，点E是AB边上的动点，则 的值为_________。‎ ‎(14)已知f（x）=m（x‎-2m）（x＋m＋3），g（x）=2N-2。若，f（x）＜0或g（x）＜0，则m的取值范围是_________。‎ 三、解答题共6小题，共80分，解答应写出文字说明，演算步骤或证明过程。‎ ‎（15）（本小题共13分）‎ 已知函数。‎ ‎（1）求f（x）的定义域及最小正周期；‎ ‎（2）求f（x）的单调递减区间。‎ ‎（16）（本小题共14分）‎ 如图1，在Rt△ABC中，∠C=90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A‎1F⊥CD，如图2。‎ （1） 求证：DE∥平面A1CB；‎ （2） 求证：A‎1F⊥BE；‎ （3） 线段A1B上是否存在点Q，使A‎1C⊥平面DEQ？说明理由。‎ ‎17（本小题共13分）‎ 近年来，某市为了促进生活垃圾的风分类处理，将生活垃圾分为厨余垃圾、可回收和其他垃圾三类，并分别设置了相应分垃圾箱，为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：‎ ‎（Ⅰ）试估计厨余垃圾投放正确的概率；‎ ‎（Ⅱ）试估计生活垃圾投放错误额概率；‎ ‎（Ⅲ）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c其中a＞0，a+b+c=600.当数据a,b,c的方差s2最大时，写出a,b,c的值（结论不要求证明），并求此时s2的值。‎ ‎（注：其中为数据x1,x2…，xn的平均数）‎ ‎（18）（本小题共13分）‎ 已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.‎ （I） 若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线，求,a,b的值；‎ （I） 当a=3,b=-9时，若函数f(x)+g(x)在区间[k,2]上的最大值为28，求k的取值范围。‎ 19 ‎(本小题共14分)‎ 已知椭圆C：+=1（a＞b＞0）的一个顶点为A （2,0），离心率为， 直线y=k(x-1)与椭圆C交与不同的两点M,N ‎（Ⅰ）求椭圆C的方程 ‎（Ⅱ）当△AMN的面积为时，求k的值 ‎ ‎ (20)（本小题共13分）‎ 设A是如下形式的2行3列的数表，‎ a b c d E f 满足性质P：a，b，c，d，e，f∈[-1,1],且a+b+c+d+e+f=0.‎ 记ri（A）为A的第i行各数之和（i=1,2），Cj（A）为第j列各数之和（j=1，2，3）；记k（A）为|r1(A)|, |r2(A)|, |c1(A)|，|c2(A)|，|c3(A)|中的最小值。‎ （I） 对如下数表A，求k（A）的值 （II） 设数表A形如 其中-1≤d≤0.求k（A）的最大值；‎ ‎（Ⅲ）对所有满足性质P的2行3列的数表A ，求k(A)的最大值