必修四平面向量常考知识点整理和复习典型高考例题分析 6页

向量复习 知识点1：‎ ‎ 两个不为零的向量，平行，①‎ ‎ ②如果可以用直角坐标系的坐标表示，那么设 ‎ ‎ ，那么 ‎ ③如果可以用两个不共线的基向量表示，比 ‎ 如说，，那么基向量前面 ‎ 的系数成比例，也就是 在这里强调其实后面两点是一样的，因为向量的坐标表示法引进前身是用直角坐标系的两个垂直的单位向量，比如，也即是，为了方便，我们写成坐标形式，而③这点其实是②的一般形式，就是③讲两个基向量推广到了不垂直的情况。‎ 用这个知识点的例题比如说：‎ ‎【例一】设与是两个不共线的向量，且向量与共线，则的值为 ．‎ ‎【解析】要求的两个向量就是用与作为基底的，那么这两个向量共线可以得到前面的系数成比例，也即是，也即 ‎【例二】在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD交于点F，若，，则=（ ）‎ A． B． ‎ ‎ C． D．‎ ‎【解析】比如说运用这个知识点首先本题的难点在于F点的位置，其在DC中的位置比例，所以首先要确定其位置在哪里，所以，我们设 那么我们就可以用一个共线来确定的值 所以我们可以用 用相同基向量表示这两个向量，然后用系数比例的关系求出这个的值 则 ‎【例三】如图，在△ABC中，点M为BC的中点，A、B、C三点坐标分别为（2，﹣2）、（5，2）、（﹣3，0），点N在AC上，且，AM与BN的交点为P，求：‎ ‎（1）点P分向量所成的比的值；‎ ‎（2）P点坐标．‎ ‎【解析】这题例题也是同样的道理，（1）主要求P点，假设,‎ 因为三点共线，所以用基向量表示，再用待定系数法求得λ的值。‎ 所以，所以分向量所成的比的值为 （2） 用比例的方法可以得到P ‎（★★总结方法：在图中有未知线段的比例不知道，就可以先设其线段比例为，然后利用一个三点共线的两向量平行来求解的值。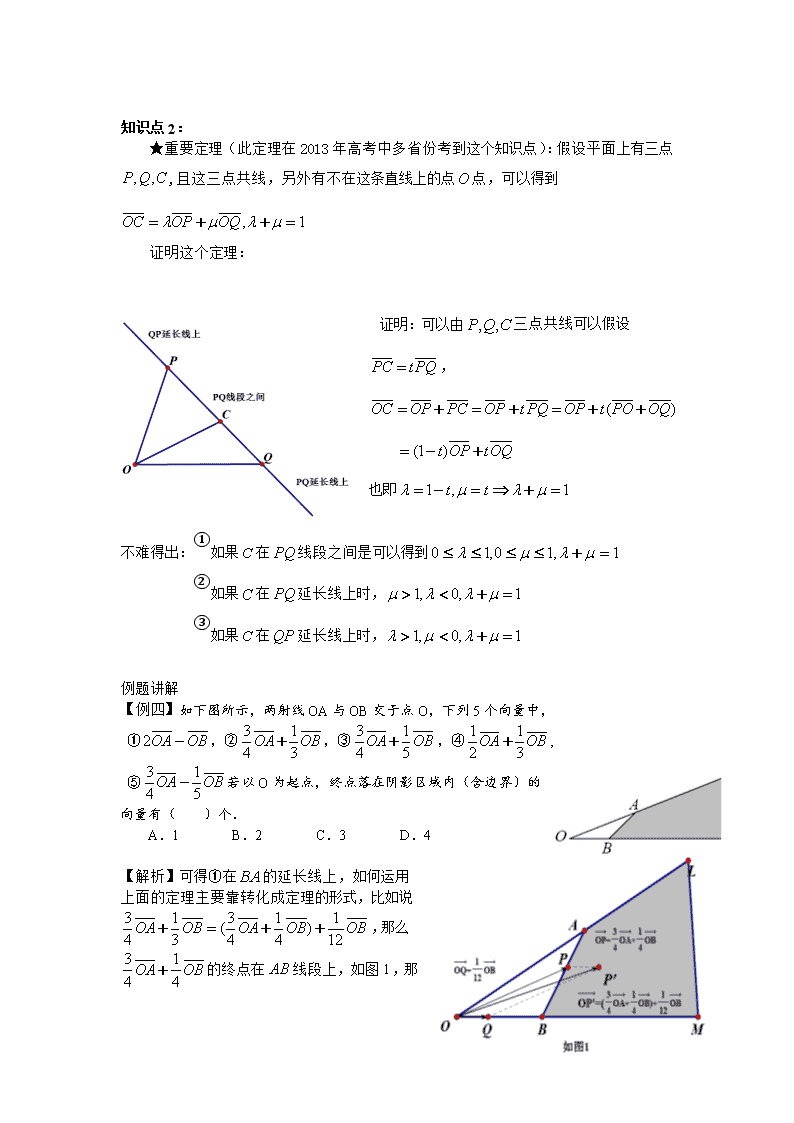）‎ 知识点2：‎ ‎★重要定理（此定理在2013年高考中多省份考到这个知识点）：假设平面上有三点,且这三点共线，另外有不在这条直线上的点点，可以得到 证明这个定理：‎ 证明：可以由三点共线可以假设， ‎ 也即 不难得出：①如果在线段之间是可以得到 ‎ ②如果在延长线上时，‎ ‎ ③如果在延长线上时，‎ 例题讲解 ‎【例四】如下图所示，两射线OA与OB交于点O，下列5个向量中，‎ ‎ ①，②，③，④,‎ ‎ ⑤若以O为起点，终点落在阴影区域内（含边界）的向量有（　　）个．‎ ‎ A．1 B．2 C．3 D．4‎ ‎【解析】可得①在的延长线上，如何运用上面的定理主要靠转化成定理的形式，比如说，那么的终点在 线段上，如图1，那么就会在如图的阴影部分内。‎ 同理可以 将③转化为 将④转化为 将⑤转化为 ‎【例五】（2013安徽卷理9）在平面直角坐标系中,O是坐标原点,两定点A,B满,则点集所表示的区域面积是 (A) ‎ (B) (C) (D)‎ ‎ 【解析】，可以得到，且两个向量的夹角为60°，如图可以将两个向量放到半径为2的圆内，如图2。‎ ‎ 且由，可得，‎ 那么当时，可知P点形成的 区域为图中灰色区域 当，将问题转化为 ‎,那么P点 形成的区域则是紫色的区域 ‎ 当，将问题转化为 ‎ ‎ ‎ ‎ 那么P点形成的区域是红色的区域 ‎ 当，将问题转化为 ‎ ‎ ‎ 那么P点形成的区域是黄色的区域 所以，综上所述可得P点形成的区域为一个长为，宽为2的矩形区域，即面积为，所以答案选D。‎ 知识点3：‎ 向量的基本要素求解：一般求解向量的基本要素，主要分为求解向量之间的夹角和向量的模长。‎ 那么要求这几个要素必须要明白其可求解的途径：‎ ①求解模长 ‎ 1）如果向量的坐标已知（前提是在直角坐标系下的坐标），那么就可 ‎ 以直接选用勾股定理求解 ‎ 2）如果向量的坐标不知道，但是用两个已知的基向量表示出来，并且已 ‎ 知基向量的模长，基向量之间的夹角，那么可以通过对模长平方来求解，‎ ‎ 比如：已知且，如果，则 ‎ ‎ ‎ ‎ 一般在不知道坐标的情况下都可以进行平方求解。‎ ‎ 3）可以用公式求解 ②夹角求解 ‎ 1）可以用公式求解 ‎ 2）★★两向量夹角的范围，两向量的夹角与三角形中角的类型的 ‎ 判断有着密切的联系：‎ ‎ 若，则该角为锐角当时，‎ ‎ 若，则该角为直角 当时， ‎ ‎ 若，则该角为钝角当，‎ 知识点4：‎ ‎1）向量的点积，如果向量有坐标，，则。‎ ‎2）向量在向量上的投影为（投影可以是负的），向量在基向量上分解，平行四边形原则。‎ ‎【例六】如图，设P、Q为△ABC内的两点，且，，＝＋，则△ABP的面积与△ABQ的面积之比为 ． ‎ N ‎ M ‎ Q P ‎ C ‎ B A ‎ ‎【解析】本题考查的是向量的平行四边形法则分解，已知，＝＋，如下图，设，，则，由平行四边形法则，知NP∥AB，‎ 所以＝，同理可得，‎ ‎ 故． ‎ ‎【例七】（2013浙江卷理7）设是边上一定点，满足，且对于边上任一点，恒有。则（ ）‎ ‎ A. B. C. D.‎ ‎【解析】本题考查向量的几何意义，也就是投影。过C点作，并且此处记,且若P点在HB之间时，记PH为负，P点在AH之间时，PH为正，所以，此处的与上述的相同，所以 当三角形确定以后，HB就为常数可以定下来，而PH为一个变量，所有把它看成一个函数，可知，当时，最小，即此时点在HB线段的中点，而由条件可知，也即此时P点与点重合，并且，可得到为HB线段的中点，则,即为AB的中点，那么CH为AB的中垂线，那么AC=AB。‎ ‎★★向量的几何意义考查一般要数形结合，考察起来题目一般难度会比较大，关键在于是否能够转化为几何问题上。‎