江苏省连云港市徐州市宿迁市高考数学三模试卷解析 31页

‎2017年江苏省连云港市、徐州市、宿迁市高考数学三模试卷 ‎　‎ 一、填空题（每题5分，满分70分，江答案填在答题纸上）‎ ‎1．已知集合A={﹣1，1，2}，B={0，1，2，7}，则集合A∪B中元素的个数为　　．‎ ‎2．设a，b∈R， =a+bi（i为虚数单位），则b的值为　　．‎ ‎3．在平面直角坐标系xOy中，双曲线﹣=1的离心率是　　．‎ ‎4．现有三张识字卡片，分别写有“中”、“国”、“梦”这三个字．将这三张卡片随机排序，则能组成“中国梦”的概率是　　．‎ ‎5．如图是一个算法的流程图，则输出的k的值为　　．‎ ‎6．已知一组数据3，6，9，8，4，则该组数据的方差是　　．‎ ‎7．已知实数x，y满足，则的取值范围是　　．‎ ‎8．若函数f（x）=2sin（2x+φ）（0＜φ＜）的图象过点（0，），则函数f（x）在[0，π]上的单调减区间是　　．‎ ‎9．在公比为q且各项均为正数的等比数列{an}中，Sn为{an}的前n项和．若a1=，且S5=S2+2，则q的值为　　．‎ ‎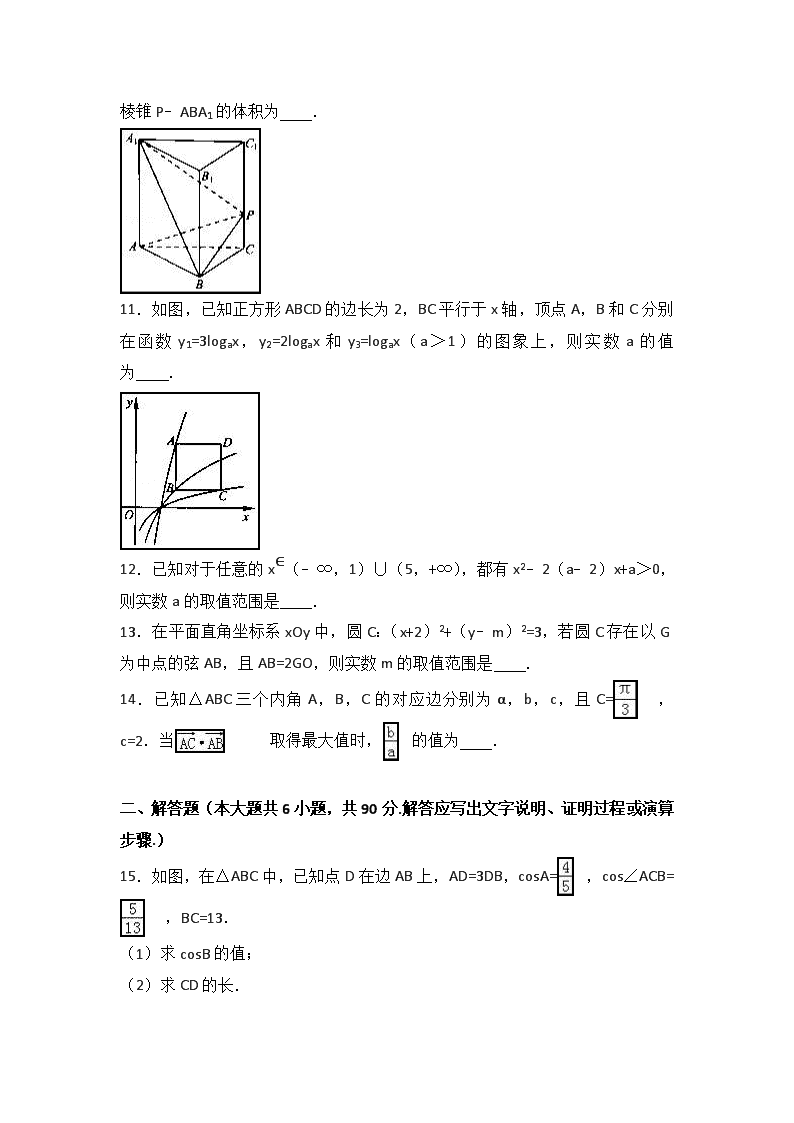10．如图，在正三棱柱ABC﹣A1B1C1中，已知AB=AA1=3，点P在棱CC1‎ 上，则三棱锥P﹣ABA1的体积为　　．‎ ‎11．如图，已知正方形ABCD的边长为2，BC平行于x轴，顶点A，B和C分别在函数y1=3logax，y2=2logax和y3=logax（a＞1）的图象上，则实数a的值为　　．‎ ‎12．已知对于任意的x∈（﹣∞，1）∪（5，+∞），都有x2﹣2（a﹣2）x+a＞0，则实数a的取值范围是　　．‎ ‎13．在平面直角坐标系xOy中，圆C：（x+2）2+（y﹣m）2=3，若圆C存在以G为中点的弦AB，且AB=2GO，则实数m的取值范围是　　．‎ ‎14．已知△ABC三个内角A，B，C的对应边分别为α，b，c，且C=，c=2．当取得最大值时，的值为　　．‎ ‎　‎ 二、解答题（本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎15．如图，在△ABC中，已知点D在边AB上，AD=3DB，cosA=，cos∠ACB=，BC=13．‎ ‎（1）求cosB的值；‎ ‎（2）求CD的长．‎ ‎16．如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，点E在棱PC上（异于点P，C），平面ABE与棱PD交于点F．‎ ‎（1）求证：AB∥EF；‎ ‎（2）若平面PAD⊥平面ABCD，求证：AE⊥EF．‎ ‎17．如图，在平面直角坐标系xOy中，已知椭圆C： +=1的左、右顶点分别为A，B，过右焦点F的直线l与椭圆C交于P，Q两点（点P在x轴上方）．‎ ‎（1）若QF=2FP，求直线l的方程；‎ ‎（2）设直线AP，BQ的斜率分别为k1，k2，是否存在常数λ，使得k1=λk2？若存在，求出λ的值；若不存在，请说明理由．‎ ‎18．某景区修建一栋复古建筑，其窗户设计如图所示．圆O的圆心与矩形ABCD对角线的交点重合，且圆与矩形上下两边相切（E为上切点），与左右两边相交（F，G为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m且≥，设∠EOF=θ，透光区域的面积为S．‎ ‎（1）求S关于θ的函数关系式，并求出定义域；‎ ‎（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好．当该比值最大时，求边AB的长度．‎ ‎19．已知两个无穷数列{an}和{bn}的前n项和分别为Sn，Tn，a1=1，S2=4，对任意的n∈N*，都有3Sn+1=2Sn+Sn+2+an．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）若{bn}为等差数列，对任意的n∈N*，都有Sn＞Tn．证明：an＞bn；‎ ‎（3）若{bn}为等比数列，b1=a1，b2=a2，求满足=ak（k∈N*）的n值．‎ ‎20．已知函数f（x）=+xlnx（m＞0），g（x）=lnx﹣2．‎ ‎（1）当m=1时，求函数f（x）的单调区间；‎ ‎（2）设函数h（x）=f（x）﹣xg（x）﹣，x＞0．若函数y=h（h（x））的最小值是，求m的值；‎ ‎（3）若函数f（x），g（x）的定义域都是[1，e]，对于函数f（x）的图象上的任意一点A，在函数g（x）的图象上都存在一点B，使得OA⊥OB，其中e是自然对数的底数，O为坐标原点，求m的取值范围．‎ ‎　‎ ‎【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答，若多做，则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-1：几何证明选讲 ‎21．如图，圆O的弦AB，MN交于点C，且A为弧MN的中点，点D在弧BM上，若∠ACN=3∠ADB，求∠ADB的度数．‎ ‎　‎ B.选修4-2：矩阵与变换 ‎22．已知矩阵A=，若A=，求矩阵A的特征值．‎ ‎　‎ C.选修4-4：坐标系与参数方程 ‎23．在极坐标系中，已知点A（2，），点B在直线l：ρcosθ+ρsinθ=0（0≤θ≤2π）上，当线段AB最短时，求点B的极坐标．‎ ‎　‎ D.选修4-5：不等式选讲 ‎24．已知a，b，c为正实数，且a3+b3+c3=a2b2c2，求证：a+b+c≥3．‎ ‎　‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]‎ ‎25．在平面直角坐标系xOy中，点F（1，0），直线x=﹣1与动直线y=n的交点为M，线段MF的中垂线与动直线y=n的交点为P．‎ ‎（Ⅰ）求点P的轨迹Г的方程；‎ ‎（Ⅱ）过动点M作曲线Г的两条切线，切点分别为A，B，求证：∠AMB的大小为定值．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎26．已知集合U={1，2，…，n}（n∈N*，n≥2），对于集合U的两个非空子集A，B，若A∩B=∅，则称（A，B）为集合U的一组“互斥子集”．记集合U的所有“互斥子集”的组数为f（n）（视（A，B）与（B，A）为同一组“互斥子集”）．‎ ‎（1）写出f（2），f（3），f（4）的值；‎ ‎（2）求f（n）．‎ ‎　‎ ‎2017年江苏省连云港市、徐州市、宿迁市高考数学三模试卷 参考答案与试题解析 ‎　‎ 一、填空题（每题5分，满分70分，江答案填在答题纸上）‎ ‎1．已知集合A={﹣1，1，2}，B={0，1，2，7}，则集合A∪B中元素的个数为　5　．‎ ‎【考点】1D：并集及其运算．‎ ‎【分析】利用并集定义直接求解．‎ ‎【解答】解：∵集合A={﹣1，1，2}，B={0，1，2，7}，‎ ‎∴A∪B={﹣1，0，1，2，7}，‎ 集合A∪B中元素的个数为5．‎ 故答案为：5．‎ ‎　‎ ‎2．设a，b∈R， =a+bi（i为虚数单位），则b的值为　1　．‎ ‎【考点】A5：复数代数形式的乘除运算．‎ ‎【分析】利用复数的运算法则、复数相等即可得出．‎ ‎【解答】解：∵a，b∈R， =a+bi（i为虚数单位），‎ ‎∴a+bi===i．‎ ‎∴b=1．‎ 故答案为：1．‎ ‎　‎ ‎3．在平面直角坐标系xOy中，双曲线﹣=1的离心率是　　．‎ ‎【考点】KC：双曲线的简单性质．‎ ‎【分析】根据题意，由双曲线的方程可得a2、b2的值，由双曲线的几何性质可得c的值，进而由双曲线的离心率公式计算可得答案．‎ ‎【解答】解：根据题意，双曲线的方程为﹣=1，‎ 则a2=4，b2=3，‎ 则c==，‎ 则其离心率e==；‎ 故答案为：．‎ ‎　‎ ‎4．现有三张识字卡片，分别写有“中”、“国”、“梦”这三个字．将这三张卡片随机排序，则能组成“中国梦”的概率是　　．‎ ‎【考点】CC：列举法计算基本事件数及事件发生的概率．‎ ‎【分析】将这三张卡片随机排序，基本事件总数为：n==6，能组成“中国梦”包含的基本事件个数m=1，由此能求出能组成“中国梦”的概率．‎ ‎【解答】解：现有三张识字卡片，分别写有“中”、“国”、“梦”这三个字．‎ 将这三张卡片随机排序，基本事件总数为：n==6，‎ 能组成“中国梦”包含的基本事件个数m=1，‎ ‎∴能组成“中国梦”的概率p=．‎ 故答案为：．‎ ‎　‎ ‎5．如图是一个算法的流程图，则输出的k的值为　6　．‎ ‎【考点】EF：程序框图．‎ ‎【分析】分析程序中各变量、各语句的作用，根据流程图所示的顺序，即可得出结论．‎ ‎【解答】解：分析流程图所示的顺序知：‎ k=2，22﹣14+10=0，‎ 不满足条件k2﹣7k+10＞0，执行循环体；‎ k=3，32﹣21+10=﹣2，‎ 不满足条件k2﹣7k+10＞0，执行循环体；‎ k=4，42﹣28+10=﹣2，‎ 不满足条件k2﹣7k+10＞0，执行循环体；‎ k=5，52﹣35+10=0，‎ 不满足条件k2﹣7k+10＞0，执行循环体；‎ k=6，62﹣42+10=4，‎ 满足条件k2﹣7k+10＞0，退出循环，输出k=6．‎ 故答案为：6．‎ ‎　‎ ‎6．已知一组数据3，6，9，8，4，则该组数据的方差是　5.2　．‎ ‎【考点】BC：极差、方差与标准差．‎ ‎【分析】利用定义求这组数据的平均数和方差即可．‎ ‎【解答】解：数据3，6，9，8，4的平均数为：‎ ‎=×（3+6+9+8+4）=6，‎ 方差为：‎ s2=×[（3﹣6）2+（6﹣6）2+（9﹣6）2+（8﹣6）2+（4﹣6）2]= =5.2．‎ 故答案为：5.2．‎ ‎　‎ ‎7．已知实数x，y满足，则的取值范围是　[，]　．‎ ‎【考点】7C：简单线性规划．‎ ‎【分析】由约束条件作出可行域，再由的几何意义，即可行域内的动点与定点O（0，0）连线的斜率求解．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 的几何意义为可行域内的动点与定点O（0，0）连线的斜率，‎ 联立方程组求得A（3，﹣1），B（3，2），‎ 又，．‎ ‎∴的取值范围是[，]．‎ 故答案为：[，]．‎ ‎　‎ ‎8．若函数f（x）=2sin（2x+φ）（0＜φ＜）的图象过点（0，），则函数f（x）在[0，π]上的单调减区间是　[，]【或（，‎ ‎）也正确】　．‎ ‎【考点】H2：正弦函数的图象．‎ ‎【分析】根据函数f（x）图象过点（0，）求出φ的值，写出f（x）解析式，‎ 再根据正弦函数的图象与性质求出f（x）在[0，π]上的单调减区间．‎ ‎【解答】解：函数f（x）=2sin（2x+φ）（0＜φ＜）的图象过点（0，），‎ ‎∴f（0）=2sinφ=，‎ ‎∴sinφ=；‎ 又∵0＜φ＜，‎ ‎∴φ=，‎ ‎∴f（x）=2sin（2x+）；‎ 令+2kπ≤2x+≤+2kπ，k∈Z，‎ ‎∴+2kπ≤2x≤+2kπ，k∈Z，‎ 解得+kπ≤x≤+kπ，k∈Z；‎ 令k=0，得函数f（x）在[0，π]上的单调减区间是[，]．‎ 故答案为：[，]【或（，）也正确】．‎ ‎　‎ ‎9．在公比为q且各项均为正数的等比数列{an}中，Sn为{an}的前n项和．若a1=，且S5=S2+2，则q的值为　　．‎ ‎【考点】89：等比数列的前n项和．‎ ‎【分析】由a1=，且S5=S2+2，q＞0．可得a3+a4+a5=（1+q+q2）=2，代入化简解出即可得出．‎ ‎【解答】解：∵a1=，且S5=S2+2，q＞0．‎ ‎∴a3+a4+a5=（1+q+q2）=2，‎ ‎∴q2+q﹣1=0，‎ 解得q=．‎ 故答案为：．‎ ‎　‎ ‎10．如图，在正三棱柱ABC﹣A1B1C1中，已知AB=AA1=3，点P在棱CC1上，则三棱锥P﹣ABA1的体积为　　．‎ ‎【考点】LF：棱柱、棱锥、棱台的体积．‎ ‎【分析】点P到平面ABA1的距离即为△ABC的高，由此能求出三棱锥P﹣ABA1的体积．‎ ‎【解答】解：∵在正三棱柱ABC﹣A1B1C1中，AB=AA1=3，点P在棱CC1上，‎ ‎∴点P到平面ABA1的距离即为△ABC的高，即为h==，‎ ‎==，‎ 三棱锥P﹣ABA1的体积为：V===．‎ 故答案为：．‎ ‎　‎ ‎11．如图，已知正方形ABCD的边长为2，BC平行于x轴，顶点A，B和C分别在函数y1=3logax，y2=2logax和y3=logax（a＞1）的图象上，则实数a的值为　　．‎ ‎【考点】4N：对数函数的图象与性质．‎ ‎【分析】设B（x，2logax），利用BC平行于x轴得出C（x2，2logax），利用AB垂直于x轴 得出 A（x，3logax），则正方形ABCD 的边长从横纵两个角度表示为logax=x2﹣x=2，求出x，再求a 即可．．‎ ‎【解答】解：设B（x，2logax），∵BC平行于x轴，∴C（x′，2logax）即logax′=2logax，∴x′=x2，‎ ‎∴正方形ABCD边长=|BC|=x2﹣x=2，解得x=2．‎ 由已知，AB垂直于x轴，∴A（x，3logax），正方形ABCD边长=|AB|=3logax﹣2logax=logax=2，即loga2=2，∴a=，‎ 故答案为：．‎ ‎　‎ ‎12．已知对于任意的x∈（﹣∞，1）∪（5，+∞），都有x2﹣2（a﹣2）x+a＞0，则实数a的取值范围是　（1，5]　．‎ ‎【考点】3W：二次函数的性质．‎ ‎【分析】对△进行讨论，利用二次函数的性质列不等式解出．‎ ‎【解答】解：△=4（a﹣2）2﹣4a=4a2﹣20a+16=4（a﹣1）（a﹣4）．‎ ‎（1）若△＜0，即1＜a＜4时，x2﹣2（a﹣2）x+a＞0在R上恒成立，符合题意；‎ ‎（2）若△=0，即a=1或a=4时，方程x2﹣2（a﹣2）x+a＞0的解为x≠a﹣2，‎ 显然当a=1时，不符合题意，当a=4时，符合题意；‎ ‎（3）当△＞0，即a＜1或a＞4时，∵x2﹣2（a﹣2）x+a＞0在（﹣∞，1）∪（5，+∞）恒成立，‎ ‎∴，解得3＜a≤5，‎ 又a＜1或a＞4，∴4＜a≤5．‎ 综上，a的范围是（1，5]．‎ 故答案为（1，5]．‎ ‎　‎ ‎13．在平面直角坐标系xOy中，圆C：（x+2）2+（y﹣m）2=3，若圆C存在以G为中点的弦AB，且AB=2GO，则实数m的取值范围是　∅　．‎ ‎【考点】J9：直线与圆的位置关系．‎ ‎【分析】求出G的轨迹方程，得两圆公共弦，由题意，圆心（﹣2，m）到直线的距离d=＜，即可求出实数m的取值范围．‎ ‎【解答】解：设G（x，y），则 ‎∵AB=2GO，‎ ‎∴2=2，‎ 化简可得x2+y2+2x﹣my+m2+=0，‎ 两圆方程相减可得2x﹣my+m2+=0‎ 由题意，圆心（﹣2，m）到直线的距离d=＜，无解，‎ 故答案为∅．‎ ‎　‎ ‎14．已知△ABC三个内角A，B，C的对应边分别为α，b，c，且C=，c=2．当取得最大值时，的值为　2+　．‎ ‎【考点】9V：向量在几何中的应用．‎ ‎【分析】根据正弦定理用A表示出b，代入 ‎=2bcosA，根据三角恒等变换化简得出当取最大值时A的值，再计算sinA，sinB得出答案．‎ ‎【解答】解：∵C=，∴B=﹣A，‎ 由正弦定理得=，‎ ‎∴b=sin（﹣A）=2cosA+sinA，‎ ‎∴=bccosA=2bcosA=4cos2A+sin2A ‎=2+2cos2A+sin2A ‎=（sin2A+cos2A）+2‎ ‎=sin（2A+）+2，‎ ‎∵A+B=，∴0＜A＜，‎ ‎∴当2A+=即A=时，取得最大值，‎ 此时，B=﹣=‎ ‎∴sinA=sin=sin（）=﹣=，‎ sinB=sin（）==．‎ ‎∴==2+．‎ 故答案为2+．‎ ‎　‎ 二、解答题（本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎15．如图，在△ABC中，已知点D在边AB上，AD=3DB，cosA=，cos∠ACB=‎ ‎，BC=13．‎ ‎（1）求cosB的值；‎ ‎（2）求CD的长．‎ ‎【考点】HT：三角形中的几何计算．‎ ‎【分析】（1）在△ABC中，求出sinA==．，sin∠ACB=．‎ 可得cosB=﹣cos（A+∠ACB）=sinAsin∠ACB﹣cosAcosB；‎ ‎（2）在△ABC中，由正弦定理得，AB=sin∠ACB．‎ 在△BCD中，由余弦定理得，CD=．‎ ‎【解答】解：（1）在△ABC中，cosA=，A∈（0，π），‎ 所以sinA==．‎ 同理可得，sin∠ACB=．‎ 所以cosB=cos[π﹣（A+∠ACB）]=﹣cos（A+∠ACB）‎ ‎=sinAsin∠ACB﹣cosAcos∠ACB ‎=；‎ ‎（2）在△ABC中，由正弦定理得，AB=sin∠ACB=．‎ 又AD=3DB，所以DB=．‎ 在△BCD中，由余弦定理得，CD=‎ ‎==9．‎ ‎　‎ ‎16．如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，点E在棱PC上（异于点P，C），平面ABE与棱PD交于点F．‎ ‎（1）求证：AB∥EF；‎ ‎（2）若平面PAD⊥平面ABCD，求证：AE⊥EF．‎ ‎【考点】LZ：平面与平面垂直的性质．‎ ‎【分析】（1）推导出AB∥CD，从而AB∥平面PDC，由此能证明AB∥EF．‎ ‎（2）推导出AB⊥AD，从而AB⊥平面PAD，进而AB⊥AF，由AB∥EF，能证明AF⊥EF．‎ ‎【解答】证明：（1）因为ABCD是矩形，所以AB∥CD．‎ 又因为AB⊄平面PDC，CD⊂平面PDC，‎ 所以AB∥平面PDC．‎ 又因为AB⊂平面ABEF，平面ABEF∩平面PDC=EF，‎ 所以AB∥EF．‎ ‎（2）因为ABCD是矩形，所以AB⊥AD．‎ 又因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，‎ AB⊂平面ABCD，所以AB⊥平面PAD．‎ 又AF⊂平面PAD，所以AB⊥AF．‎ 又由（1）知AB∥EF，所以AF⊥EF．‎ ‎　‎ ‎17．如图，在平面直角坐标系xOy中，已知椭圆C： +=1的左、右顶点分别为A，B，过右焦点F的直线l与椭圆C交于P，Q两点（点P在x轴上方）．‎ ‎（1）若QF=2FP，求直线l的方程；‎ ‎（2）设直线AP，BQ的斜率分别为k1，k2，是否存在常数λ，使得k1=λk2？若存在，求出λ的值；若不存在，请说明理由．‎ ‎【考点】KL：直线与椭圆的位置关系．‎ ‎【分析】（1）由椭圆方程求出a，b，c，可得F的坐标，设P（x1，y1），Q（x2，y2），直线l的方程为x=my+1，代入椭圆方程，求得P，Q的纵坐标，再由向量共线的坐标表示，可得m的方程，解方程可得m，进而得到直线l的方程；‎ ‎（2）运用韦达定理可得y1+y2，y1y2，my1y2，由A（﹣2，0），B（2，0），P（x1，y1），Q（x2，y2），x1=my1+1，x2=my2+1，‎ 运用直线的斜率公式，化简整理计算可得常数λ的值，即可判断存在．‎ ‎【解答】解：（1）因为a2=4，b2=3，所以c==1，‎ 所以F的坐标为（1，0），‎ 设P（x1，y1），Q（x2，y2），直线l的方程为x=my+1，‎ 代入椭圆方程+=1，得（4+3m2）y2+6my﹣9=0，‎ 则y1=，y2=．‎ 若QF=2FP，即=2，‎ 则+2•=0，‎ 解得m=，‎ 故直线l的方程为x﹣2y﹣=0．‎ ‎（2）由（1）知，y1+y2=﹣，y1y2=﹣，‎ 所以my1y2=﹣=（y1+y2），‎ 由A（﹣2，0），B（2，0），P（x1，y1），Q（x2，y2），x1=my1+1，x2=my2+1，‎ 所以=•===，‎ 故存在常数λ=，使得k1=k2．‎ ‎　‎ ‎18．某景区修建一栋复古建筑，其窗户设计如图所示．圆O的圆心与矩形ABCD对角线的交点重合，且圆与矩形上下两边相切（E为上切点），与左右两边相交（F，G为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m且≥，设∠EOF=θ，透光区域的面积为S．‎ ‎（1）求S关于θ的函数关系式，并求出定义域；‎ ‎（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好．当该比值最大时，求边AB的长度．‎ ‎【考点】HN：在实际问题中建立三角函数模型．‎ ‎【分析】（1）过点O作OH⊥FG于H，写出透光面积S关于θ的解析式S，并求出θ的取值范围；‎ ‎（2）计算透光区域与矩形窗面的面积比值，构造函数，利用导数判断函数的单调性，‎ 求出比值最大时对应边AB的长度．‎ ‎【解答】解：（1）过点O作OH⊥FG于H，∴∠OFH=∠EOF=θ；‎ 又OH=OFsinθ=sinθ，‎ FH=OFcosθ=cosθ，‎ ‎∴S=4S△OFH+4S阴影OEF=2sinθcosθ+4×θ=sin2θ+2θ；‎ ‎∵≥，∴sinθ≥，∴θ∈[，）；‎ ‎∴S关于θ的函数关系式为S=sin2θ+2θ，θ∈[，）；‎ ‎（2）由S矩形=AD•AB=2×2sinθ=4sinθ，‎ ‎∴=+，‎ 设f（θ）=+，θ∈[，），‎ 则f′（θ）=﹣sinθ+‎ ‎=‎ ‎=‎ ‎=；‎ ‎∵≤θ＜，∴sin2θ≤，‎ ‎∴sin2θ﹣θ＜0，‎ ‎∴f′（θ）＜0，‎ ‎∴f（θ）在θ∈[，）上是单调减函数；‎ ‎∴当θ=时f（θ）取得最大值为+，‎ 此时AB=2sinθ=1（m）；‎ ‎∴S关于θ的函数为S=sin2θ+2θ，θ∈[，）；所求AB的长度为1m．‎ ‎　‎ ‎19．已知两个无穷数列{an}和{bn}的前n项和分别为Sn，Tn，a1=1，S2=4，对任意的n∈N*，都有3Sn+1=2Sn+Sn+2+an．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）若{bn}为等差数列，对任意的n∈N*，都有Sn＞Tn．证明：an＞bn；‎ ‎（3）若{bn}为等比数列，b1=a1，b2=a2，求满足=ak（k∈N*）的n值．‎ ‎【考点】8E：数列的求和；8H：数列递推式．‎ ‎【分析】（1）运用数列的递推式和等差数列的定义和通项公式，即可得到所求；‎ ‎（2）方法一、设数列{bn}的公差为d，求出Sn，Tn．由恒成立思想可得b1＜1，求出an﹣bn，判断符号即可得证；‎ 方法二、运用反证法证明，设{bn}的公差为d，假设存在自然数n0≥2，使得a≤b，推理可得d＞2，作差Tn﹣Sn，推出大于0，即可得证；‎ ‎（3）运用等差数列和等比数列的求和公式，求得Sn，Tn，化简，推出小于3，结合等差数列的通项公式和数列的单调性，即可得到所求值．‎ ‎【解答】解：（1）由3Sn+1=2Sn+Sn+2+an，得2（Sn+1﹣Sn）=Sn+2﹣Sn+1+an，‎ 即2an+1=an+2+an，所以an+2﹣an+1=an+1﹣an．‎ 由a1=1，S2=4，可知a2=3．‎ 所以数列{an}是以1为首项，2为公差的等差数列．‎ 故{an}的通项公式为an=1+2（n﹣1）=2n﹣1，n∈N*．‎ ‎（2）证法一：设数列{bn}的公差为d，‎ 则Tn=nb1+n（n﹣1）d，‎ 由（1）知，Sn=n（1+2n﹣1）=n2．‎ 因为Sn＞Tn，所以n2＞nb1+n（n﹣1）d，‎ 即（2﹣d）n+d﹣2b1＞0恒成立，‎ 所以，即，‎ 又由S1＞T1，得b1＜1，‎ 所以an﹣bn=2n﹣1﹣b1﹣（n﹣1）d=（2﹣d）n+d﹣1﹣b1≥2﹣d+d﹣1﹣b1=1﹣b1＞0．‎ 所以an＞bn，得证．‎ 证法二：设{bn}的公差为d，假设存在自然数n0≥2，使得a≤b，‎ 则a1+2（n0﹣1）≤b1+（n0﹣1）d，即a1﹣b1≤（n0﹣1）（d﹣2），‎ 因为a1＞b1，所以d＞2．‎ 所以Tn﹣Sn=nb1+n（n﹣1）d﹣n2=（d﹣1）n2+（b1﹣d）n，‎ 因为d﹣1＞0，所以存在N∈N*，当n＞N时，Tn﹣Sn＞0恒成立．‎ 这与“对任意的n∈N*，都有Sn＞Tn”矛盾！‎ 所以an＞bn，得证．‎ ‎（3）由（1）知，Sn=n2．因为{bn}为等比数列，‎ 且b1=1，b2=3，‎ 所以{bn}是以1为首项，3为公比的等比数列．‎ 所以bn=3n﹣1，Tn=（3n﹣1）．‎ 则===3﹣，‎ 因为n∈N*，所以6n2﹣2n+2＞0，所以＜3．‎ 而ak=2k﹣1，所以=1，即3n﹣1﹣n2+n﹣1=0（*）．‎ 当n=1，2时，（*）式成立；‎ 当n≥2时，设f（n）=3n﹣1﹣n2+n﹣1，‎ 则f（n+1）﹣f（n）=3n﹣（n+1）2+n﹣（3n﹣1﹣n2+n﹣1）=2（3n﹣1﹣n）＞0，‎ 所以0=f（2）＜f（3）＜…＜f（n）＜…，‎ 故满足条件的n的值为1和2．‎ ‎　‎ ‎20．已知函数f（x）=+xlnx（m＞0），g（x）=lnx﹣2．‎ ‎（1）当m=1时，求函数f（x）的单调区间；‎ ‎（2）设函数h（x）=f（x）﹣xg（x）﹣，x＞‎ ‎0．若函数y=h（h（x））的最小值是，求m的值；‎ ‎（3）若函数f（x），g（x）的定义域都是[1，e]，对于函数f（x）的图象上的任意一点A，在函数g（x）的图象上都存在一点B，使得OA⊥OB，其中e是自然对数的底数，O为坐标原点，求m的取值范围．‎ ‎【考点】6E：利用导数求闭区间上函数的最值；6B：利用导数研究函数的单调性．‎ ‎【分析】（1）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可；‎ ‎（2）求出h（x）的导数，解关于导函数的不等式，求出函数的单调区间，求出h（x）的最小值，从而求出m的值即可；‎ ‎（3）根据OA和OB的关系，问题转化为﹣x2lnx≤m≤x2（e﹣lnx）在[1，e]上恒成立，设p（x）=﹣x2lnx，根据函数的单调性求出m≥p（1）=，设q（x）=x2（e﹣lnx），根据函数的单调性求出m≤q（1），从而求出m的范围即可．‎ ‎【解答】解：（1）当m=1时，f（x）=+xlnx，f′（x）=+lnx+1，‎ 因为f′（x）在（0，+∞）上单调增，且f′（1）=0，‎ 所以当x＞1时，f′（x）＞0；当0＜x＜1时，f′（x）＜0，‎ 所以函数f（x）的单调增区间是（1，+∞）．‎ ‎（2）h（x）=+2x﹣，则h′（x）=，令h′（x）=0，得x=，‎ 当0＜x＜时，h′（x）＜0，函数h（x）在（0，）上单调减；‎ 当x＞时，h′（x）＞0，函数h（x）在（，+∞）上单调增．‎ 所以[h（x）]min=h（）=2m﹣，‎ ‎①当（2m﹣1）≥，即m≥时，函数y=h（h（x））的最小值 h（2m﹣）= [+2（2﹣1）﹣1]= ，‎ 即17m﹣26+9=0，解得=1或=（舍），所以m=1；‎ ‎②当0＜（2﹣1）＜，即＜m＜时，‎ 函数y=h（h（x））的最小值h（）=（2﹣1）=，解得=（舍），‎ 综上所述，m的值为1．‎ ‎（3）由题意知，KOA=+lnx，KOB=，‎ 考虑函数y=，因为y′=在[1，e]上恒成立，‎ 所以函数y=在[1，e]上单调增，故KOB∈[﹣2，﹣]，‎ 所以KOA∈[，e]，即≤+lnx≤e在[1，e]上恒成立，‎ 即﹣x2lnx≤m≤x2（e﹣lnx）在[1，e]上恒成立，‎ 设p（x）=﹣x2lnx，则p′（x）=﹣2lnx≤0在[1，e]上恒成立，‎ 所以p（x）在[1，e]上单调减，所以m≥p（1）=，‎ 设q（x）=x2（e﹣lnx），‎ 则q′（x）=x（2e﹣1﹣2lnx）≥x（2e﹣1﹣2lne）＞0在[1，e]上恒成立，‎ 所以q（x）在[1，e]上单调增，所以m≤q（1）=e，‎ 综上所述，m的取值范围为[，e]．‎ ‎　‎ ‎【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答，若多做，则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-1：几何证明选讲 ‎21．如图，圆O的弦AB，MN交于点C，且A为弧MN的中点，点D在弧BM上，若∠ACN=3∠ADB，求∠ADB的度数．‎ ‎【考点】NB：弦切角．‎ ‎【分析】连结AN，DN．利用圆周角定理，结合∠ACN=3∠ADB，求∠ADB的度数．‎ ‎【解答】解：连结AN，DN．‎ 因为A为弧MN的中点，所以∠ANM=∠ADN．‎ 而∠NAB=∠NDB，‎ 所以∠ANM+∠NAB=∠ADN+∠NDB，‎ 即∠BCN=∠ADB．‎ 又因为∠ACN=3∠ADB，‎ 所以∠ACN+∠BCN=3∠ADB+∠ADB=180°，‎ 故∠ADB=45°．‎ ‎　‎ B.选修4-2：矩阵与变换 ‎22．已知矩阵A=，若A=，求矩阵A的特征值．‎ ‎【考点】OV：特征值与特征向量的计算．‎ ‎【分析】利用矩阵的乘法，求出a，d，利用矩阵A的特征多项式为0，求出矩阵A的特征值．‎ ‎【解答】解：因为A==，‎ 所以，解得a=2，d=1．‎ 所以矩阵A的特征多项式为f（λ）==（λ﹣2）（λ﹣1）﹣6=（λ﹣4）（λ+1），‎ 令f（λ）=0，解得矩阵A的特征值为λ=4或﹣1．‎ ‎　‎ C.选修4-4：坐标系与参数方程 ‎23．在极坐标系中，已知点A（2，），点B在直线l：ρcosθ+ρsinθ=0（0≤θ≤2π）上，当线段AB最短时，求点B的极坐标．‎ ‎【考点】Q4：简单曲线的极坐标方程．‎ ‎【分析】点A（2，）的直角坐标为（0，2），直线l的直角坐标方程为x+y=0．AB最短时，点B为直线x﹣y+2=0与直线l的交点，求出交点，进而得出．‎ ‎【解答】解：以极点为原点，极轴为x轴正半轴，建立平面直角坐标系，‎ 则点A（2，）的直角坐标为（0，2），直线l的直角坐标方程为x+y=0．‎ AB最短时，点B为直线x﹣y+2=0与直线l的交点，‎ 联立，得，所以点B的直角坐标为（﹣1，1）．‎ 所以点B的极坐标为．‎ ‎　‎ D.选修4-5：不等式选讲 ‎24．已知a，b，c为正实数，且a3+b3+c3=a2b2c2，求证：a+b+c≥3．‎ ‎【考点】R6：不等式的证明．‎ ‎【分析】利用基本不等式的性质进行证明．‎ ‎【解答】证明：∵a3+b3+c3=a2b2c2，a3+b3+c3≥3abc，‎ ‎∴a2b2c2≥3abc，∴abc≥3，‎ ‎∴a+b+c≥3≥3．‎ 当且仅当a=b=c=时，取“=”．‎ ‎　‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]‎ ‎25．在平面直角坐标系xOy中，点F（1，0），直线x=﹣1与动直线y=n的交点为M，线段MF的中垂线与动直线y=n的交点为P．‎ ‎（Ⅰ）求点P的轨迹Г的方程；‎ ‎（Ⅱ）过动点M作曲线Г的两条切线，切点分别为A，B，求证：∠AMB的大小为定值．‎ ‎【考点】K8：抛物线的简单性质．‎ ‎【分析】（Ⅰ）连接PF，运用中垂线的性质可得|MP|=|PF|，再由抛物线的定义可得点P的轨迹方程；‎ ‎（Ⅱ）求得M（﹣1，n），过点M的切线斜率存在，设为k，则切线方程为：y﹣n=k（x+1），联立抛物线的方程，消去y，运用相切的条件：判别式为0，再由韦达定理，结合两直线垂直的条件：斜率之积为﹣1，即可得证．‎ ‎【解答】解：（Ⅰ）据题意，MP⊥直线x=﹣1，‎ ‎∴|MP|为点P到直线x=﹣1的距离，‎ 连接PF，∵P为线段MF的中垂线与直线y=n的交点，‎ ‎∴|MP|=|PF|，‎ ‎∴P点的轨迹是抛物线，焦点为F（1，0），准线为直线x=﹣1，‎ ‎∴曲线Г的方程为y2=4x；‎ ‎（Ⅱ）证明：据题意，M（﹣1，n），过点M的切线斜率存在，设为k，‎ 则切线方程为：y﹣n=k（x+1），‎ 联立抛物线方程 可得ky2﹣4y+4k+4n=0，‎ 由直线和抛物线相切，‎ 可得△=16﹣4k（4k+4n）=0，‎ 即k2+kn﹣1=0，（*）‎ ‎∵△=n2+4＞0，∴方程（*）存在两个不等实根，设为k1，k2，‎ ‎∵k1=kAM，k2=kBM，‎ 由方程（*）可知，kAM•kBM=k1•k2=﹣1，‎ ‎∴切线AM⊥BM，∴∠AMB=90°，结论得证．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎26．已知集合U={1，2，…，n}（n∈N*，n≥2），对于集合U的两个非空子集A，B，若A∩B=∅，则称（A，B）为集合U的一组“互斥子集”．记集合U的所有“互斥子集”的组数为f（n）（视（A，B）与（B，A）为同一组“互斥子集”）．‎ ‎（1）写出f（2），f（3），f（4）的值；‎ ‎（2）求f（n）．‎ ‎【考点】1H：交、并、补集的混合运算．‎ ‎【分析】（1）直接由“互斥子集”的概念求得f（2），f（3），f（4）的值；‎ ‎（2）由题意，任意一个元素只能在集合A，B，C=CU（A∪B）之一中，求出这n个元素在集合A，B，C中的个数，再求出A、B分别为空集的种数，则f（n）可求．‎ ‎【解答】解：（1）f（2）=1，f（3）=6，f（4）=25；‎ ‎（2）任意一个元素只能在集合A，B，C=CU（A∪B）之一中，‎ 则这n个元素在集合A，B，C中，共有3n种；‎ 其中A为空集的种数为2n，B为空集的种数为2n，‎ ‎∴A，B均为非空子集的种数为3n﹣2n+1+1，‎ 又（A，B）与（B，A）为一组“互斥子集”，‎ ‎∴f（n）=．‎ ‎　‎